隧道渗漏诱发的分数阶黏弹性土体固结沉降分析

2022-06-19张治国毛敏东张成平李振波潘玉涛吴钟腾

东南大学学报（自然科学版） 2022年3期

张治国毛敏东张成平李振波潘玉涛吴钟腾

(1上海理工大学环境与建筑学院, 上海 200093)(2 自然资源部丘陵山地地质灾害防治重点实验室, 福州 350002)(3山东省海洋生态环境与防灾减灾重点实验室, 青岛 266061)(4 北京交通大学城市地下工程教育部重点实验室, 北京 100044)(5 新加坡国立大学土木与环境工程系, 新加坡 119077)

在软土地区盾构隧道实际运营过程中,地下水可通过管片接缝、螺栓孔、注浆孔等进入隧道,不可避免地会导致盾构隧道衬砌出现局部渗漏水现象,致使衬砌发生破坏.同时,隧道衬砌的局部渗漏会改变土层中超孔隙水压力分布和消散,促进地层长期固结沉降,从而威胁隧道结构及邻近构筑物的安全.因此,深入分析黏弹性地层地铁盾构隧道衬砌渗漏诱发土体的固结沉降变形,具有重要的研究意义.

目前,针对盾构隧道渗漏引起的地层沉降研究方法主要包括现场试验[1-2]、数值模拟[3-5]和理论解析[6-12]等.在理论解析方面,Li[6]引入半渗透边界条件,解决了考虑渗透性边界的隧道周边超孔隙水压力消散问题.张治国等[8]解决了衬砌长期渗漏影响下盾构隧道施工扰动诱发的超孔隙水压力解和地表固结沉降问题.上述研究均假定土体为弹性体,忽略了土体的黏弹性.为考虑土体流变特性,詹美礼等[9]和张冬梅等[10]采用三元件Merchant流变模型描述土体流变性,基于复变函数对地层长期固结沉降进行了预测分析.童磊等[11]根据Burgers四元件流变模型和Terzaghi-Rendulic固结理论,分析了衬砌完全排水和完全不排水的情况下超孔隙水压力.这些研究虽然考虑了盾构隧道渗漏诱发土体固结问题中的地层流变特性,但大多是基于整数阶流变模型,而整数阶模型通常需要较多的元件组合才能获得较好的精度.分数阶流变模型是整数阶流变模型的进一步扩展.文献[13-15]分别采用不同类型的分数阶流变模型,探究不同地区的软土中孔隙水压力消散和土体固结问题,发现该模型可通过相对较少的参数来描述土体的流变特性.然而,目前在研究盾构隧道渗漏诱发土体固结沉降问题时较少采用分数阶流变模型.

鉴于此,本文采用基于Caputo分数阶导数的Merchant三元件流变模型来描述软黏土的流变特性.假定隧道衬砌为半渗透边界,耦合Terzaghi-Rendulic固结理论,通过保角映射、分离变量法、Laplace变换和逆变换等数学方法,推导出黏弹性软土隧道渗漏诱发的地层固结沉降解.利用工程算例验证本文方法的合理性,并研究了分数阶阶次和土体与衬砌渗透比对土体中超孔隙水压力消散和固结沉降的影响规律.

1 问题描述

1.1 计算模型与基本假定

对于饱和黏弹性软土地层中衬砌半渗透边界盾构隧道渗漏引起的长期土体固结沉降问题,理论上可将其简化为二维平面应变问题.令h为隧道中心埋深,r1和r2分别为隧道衬砌的内、外半径,以隧道中心正上方地表处为坐标原点建立如图1所示的直角坐标系.

图1 计算模型示意图

简化后的固结问题包含以下基本假定:

1) 隧道满足平面应变条件,在纵向上的长度足够长,隧道衬砌结构为半渗透边界[6];

2) 土体为各向同性均质连续的饱和黏弹性体,其应力-应变关系采用基于Caputo分数阶导数的Merchant三元件流变模型来描述;

3) 孔隙水的流动符合Darcy定律;

4) 土体变形为小变形,故不计变形对坐标的影响;

5) 土体固结服从Terzaghi-Rendulic二维固结理论,土体中各点总应力不随时间变化.

1.2 分数阶Merchant流变模型

图2(a)展示了经典的三元件黏弹性流变模型,即整数阶Merchant模型,为一个Kelvin模型和一个弹性元件串联而成,共包含弹性体中的弹性模量Eh、Kelvin体中的弹性模量Ek和黏滞系数ηk三个参数.本文将整数阶模型的黏壶元件替换为弹壶元件(见图2(b)),采用分数阶Merchant三元件流变模型来描述流变特性.图中,β=ηk/Ek为黏滞时间;α为分数阶次,是影响土体蠕变特性的一个重要参数.当α=1时,元件为黏壶元件,表现为理想牛顿流体;当α=0时,元件为弹簧元件,表现为线弹性固体;当0<α<1时,元件为弹壶元件,表现为分数阶黏弹性体.因此,α描述了土体从固体到流动状态的性质,反映了土体的多种性质状态,使其具有一定的物理意义.

(a) 整数阶

本文选取基于Caputo分数阶导数的Merchant模型.弹壶元件的本构关系式为[16-17]

(1)

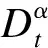
(2)

式中,Γ(x)为Gamma函数,x的实部Re(x)>0,且

(3)

因此,分数阶Merchant三元件流变模型的本构方程可表示为

(4)

式中,ε和σ分别为总应变和总应力;εh和εk分别为弹性体和Kelvin体的应变.

根据分数阶微积分Laplace变换公式可得

(5)

式中,s为复变量.

对式(4)进行Laplace变换,整理后可得

(6)

根据黏弹性力学知识可知,在小应变条件下,黏弹性体的积分型本构关系为

(7)

式中,J(t)为柔度函数.

联立式(1)、(6)、(7),通过Laplace逆变换,可得分数阶Merchant流变模型的柔度函数为

(8)

显然,当α=1时,式(8)可退化为整数阶Merchant流变模型的柔度函数;当α=0时,式(8)可退化为线弹性模型的柔度函数.

2 固结沉降控制方程

根据有效应力原理,假定土体法向总应力之和不变,可得

Θ=σx+σy+σz

(9)

(10)

式中,Θ为土体法向总应力;σx、σy和σz分别为土体的三向应力;σ′为土体有效应力;u为土体超孔隙水压力.

饱和黏弹性土体的体积应变[9,18]为

(11)

式中,μ为泊松比.

由Terzaghi-Rendulic二维固结理论可知,Θ不随时间t变化,对式(11)两边关于时间t求偏导可得

(12)

根据连续应变条件的基本假设,得到饱和黏弹性土体的连续性方程为

(13)

式中,γw为水的密度;ks为土体渗透系数.

联立式(9)、(10)、(12)、(13),可得满足分数阶Merchant三元件流变模型的黏弹性饱和软土的固结沉降控制方程,再结合式(8),通过Laplace变化可得

(14)

3 土体超孔隙水压消散方程

3.1 保角映射

本文研究的是含圆孔的一个半无限空间平面应变问题(见图1).考虑到数学上求解困难,采用保角变化ω(ζ),将z平面隧道外的土体区域映射为ζ平面内的圆环域(见图3),原z平面上的点A、B、C、D分别对应ζ平面的点A′、B′、C′、D′.根据z平面中隧道中心埋深h和隧道外半径r2，可求得圆环域的隧道半径为

(15)

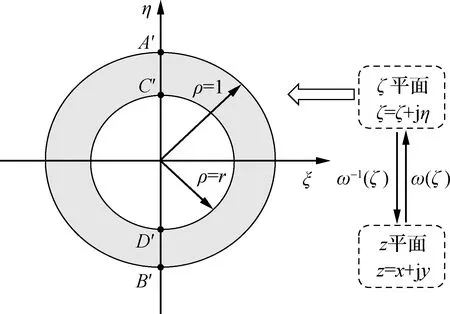
图3 映射后区域

保角映射函数为

(16)

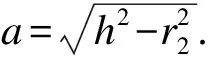
根据ζ平面内极坐标的转换关系ξ=ρcosθ和η=ρsinθ,可得复平面ζ和原平面z上相应变量的对应关系为

(17)

将式(17)代入式(14),可得经过保角变换后的ζ平面内固结控制方程为

(18)

根据Li[6]提出的半渗透边界条件,衬砌与土体的相对渗透系数可表示为

(19)

式中,k1和ks分别为隧道衬砌和土体的渗透系数.

衬砌半渗透条件下对应的边界及初始条件为

(20)

3.2 控制方程求解

采用分离变量法,求解基于分数阶Merchant流变模型的固结控制方程式(18)、衬砌半渗透边界条件及初始条件式(20).将u(ρ,θ,t)=W(ρ,θ)T(t)代入控制方程式(18)可得

(21)

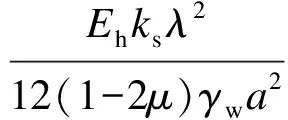
(22)

式中,λ为泛定方程的特征值,且λ>0.

对于式(21),边界条件的极坐标形式为

(23)

对于式(22),初始条件为

T(t)|t=0=1

(24)

(25)

方程(25)的通解为

W(χ)=GJ0(λχ)+QN0(λχ)

(26)

式中,J0(λχ)为零阶Bessel函数;N0(λχ)为零阶Neumann函数;G、Q为待定系数,由边界条件确定.

将式(23)代入式(26)中可得

(27)

式中

(28)

(29)

式中,λi表示第i个特征值;J1为一阶Bessel函数;N1为一阶Neumann函数.

根据Cramer法则,λi满足如下特征方程:

(30)

对于每一个确定的θ值,式(30)都可以通过逐步搜索法[8]求得特征值组成的集合{λ1,λ2,λ3,…,λi}.将某个特征值λi代入式(27)可得

(31)

将式(31)代入式(26)可得

Giψi(ρ,θ)

(32)

式中,Gi为待定系数,根据边界条件获得;ψi(ρ,θ)为关于ρ和θ的函数.

根据边界条件T(t)|t=0=1,可得初始超孔隙水压为

(33)

根据Bessel函数性质可知,特征值不同的特征函数在[r,1]上加权正交.因此,在式(33)等号两边同乘χWm(χ),并在[r,1]区间积分可得

(34)

将式(32)和式(33)代入式(34),可求得

(35)

式中,u0为初始超孔隙水压,且[11-12]

(36)

式中,P为隧道衬砌外壁上的初始超孔隙水压力.

将特征值λi代入式(22),结合边界条件式(24),可得

(37)

求解式(37)中的L(Ti),并进行Laplace逆变换可得

(38)

采用精确度较高的Crump反演方法[18]对式(38)进行求解,有

(39)

式中,Tc为Laplace逆变换计算时间周期,一般取最大时间的2倍;c=φ-lne/(2Tc),本文选取误差参数φ=0、相对误差e=0.001进行计算.

将式(32)和式(39)代入u(ρ,θ,t)=W(ρ,θ)T(t),则可得到超孔隙水压力表达式为

(40)

3.3 土体固结沉降求解

对于平面应变问题,体应变可表示为

εv=εx+εy

(41)

Merchant三元件黏弹性土体的本构关系为

(42)

式中,εx和εy分别为水平应力和竖向应力.

土体的侧向压力为

σx=K0σy

(43)

式中,K0为静止土压力系数.

因此,对于某一时刻t,将式(40)代入式(11)中,可得体应变εv,再结合式(41)、(42)和(43),可得土体中任意一点任意时刻的竖向应变εy.由此便可求解出任意时刻t隧道中心线处的地表固结沉降为

(44)

此外,根据文献[7],地表沉降可以通过Peck[19]提出的公式进行修正拓展.因此,地表固结沉降槽的公式为

(45)

式中,l为距隧道轴线的水平距离;Sl(t)为距隧道轴线l处的地表沉降值;is为地表沉降槽宽度系数.

根据文献[20],地表以下土层固结沉降可通过正态分布曲线描述为

(46)

式中,H为距地表的竖向距离;Sl,H(t)为t时刻地表以下隧道上方土体的固结沉降;SH(t)为隧道正上方土体的固结沉降;iH为深层土体沉降槽宽度系数.

根据SH(t)/S(t)=is/iH,将式(46)代入式(45),可得任意时刻地表以下隧道上方土体的固结沉降值为

(47)

4 算例验证

为验证本文理论解析解的可靠性和适用性,将本文计算结果与广州地铁2号线工程实测数据[21]进行对比分析.隧道的几何参数和物理参数为[21]:h=29.3 m;r2=3 m;r1=2.7 m;ks=2.1×10-10m/s;γ=18.1 kN/m3;k1/ks=0.028;Eh=18 MPa;Ek=23 MPa;ηk=28 GPa·d;泊松比为0.39.在具体工程中,可根据实际土样的固结沉降试验数据拟合得到分数阶阶次α.

图4为广州地铁2号线盾构施工某断面完成后100 d的地表和深层土体沉降对比图.经反复试算,本工程的分数阶阶次α取0.68较为适宜.由图4(a)可以看出,当α=0.68时,曲线与实测值总体上较为吻合;当α=0.50,0.80时,曲线与实测值存在明显偏差.α越大,沉降值也越大,分数阶阶次对沉降存在显著影响.由图4(b)可以看出,实测值与本文解析值较为吻合,且随着深度的增加,深层土体沉降均逐渐增大,但距离隧道较远处,土体沉降逐渐减小至零.总体来说,通过与实测数据的对比,验证了本文解析解的可靠性,对工程具有一定的参考价值.

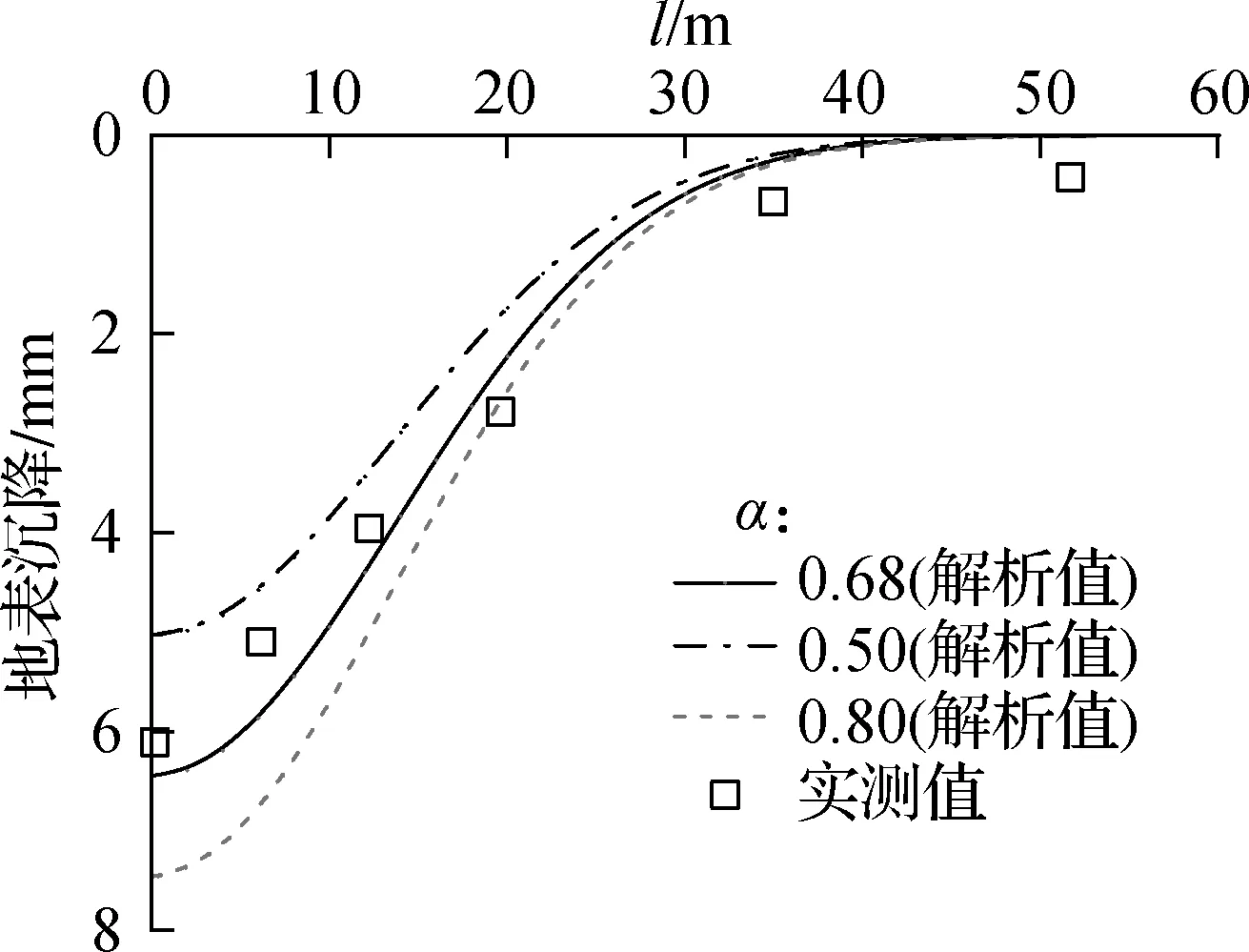
(a) 地表

5 参数分析

为分析基于Caputo分数阶导数Merchant流变模型的黏弹性软土隧道诱发超孔压消散和土体长期固结沉降问题,对分数阶导数阶次α和渗透比k1/ks进行参数分析.隧道基本参数设置如下:h=15 m;r2=3.1 m;r1=2.75 m;γ=18 kN/m3;Eh=10 MPa;Ek=20 MPa;ηk=0.5 GPa·d;洞周初始孔隙孔压力值P=30 kPa.

5.1 渗透比和分数阶阶次对超孔隙水压力的影响

为探究渗透比对超孔隙水压消散的影响,选取分数阶阶次α=0.5,对不同渗透比(k1/ks=0,0.001,0.01,0.1,1)进行参数分析.图5给出了不同渗透比影响下超孔压在隧道拱顶处的超孔隙水压力随时间消散的对比图.由图可知,随着时间的逐步推移,超孔隙水压力在较短时间内发生显著消散;消散到约初始超孔隙水压力的1/8时,曲线减幅明显放缓,后逐渐减小至零.此外,随着衬砌与土体渗透比k1/ks的增大,该位置处超孔隙水压开始消散的时间更早,对应的超孔隙水压力越小.当k1/ks=0(完全不渗透)和k1/ks=0.001时,超孔隙水压力消散曲线基本一致,即当衬砌与土体的渗透比足够小时,可以看作完全不渗透边界.当k1/ks=∞(完全渗透)和k1/ks=1时,超孔隙水压力消散曲线也基本一致,即当衬砌与土体的渗透比大于1时,可看作完全渗透边界.

图5 不同渗透比对拱顶处超孔隙水压力消散的影响

为分析分数阶流变模型的阶次对超孔隙水压消散的影响,选取k1/ks=0.01，0.1,对不同分数阶阶次(α=0.1，0.3，0.5，0.7，0.9)进行参数分析.图6给出了不同分数阶阶次影响下超孔隙水压随时间消散对比图.由图可知,随着时间的推移,超孔隙水压力逐渐消散.在不同的分数阶阶次影响下,超孔隙水压随时间消散曲线出现相互交错的现象.在超孔隙水压消散初期(13 d之前),α越大,超孔隙水压力消散越快,超孔隙水压力越小;在超孔隙水压消散后期(13 d之后),α越大,超孔隙水压消散越慢,超孔隙水压力越大.这一现象主要是由于分数阶黏壶元件的力学特性所引起的.α在0和1之间变化,对应的受力特性在理想固体和理想流体之间变化.在超孔压消散初期,变形率对有效应力起主导作用,随着α的增大,受力特性越接近于理想流体,力的大小受变形率影响增大,引起的土体有效应力也增大,土体中超孔压消散越快;反之,在超孔压消散后期,饱和软土的变形得到了充分发展,对土体有效应力起主导作用,随着α的减小,受力特性越接近理想固体,力的大小受变形影响更为明显,引起的土体有效应力增大,土体中的超孔压消散越快.总体而言,在不同的消散阶段,α对超孔隙水压的消散特性不同.

(a) k1/ks=0.01

5.2 分数阶阶次对地表沉降的影响

为探究分数阶Merchant流变模型中分数阶阶次对地表沉降的影响,选取k1/ks=0.01,对不同分数阶阶次(α=0.1，0.3，0.5，0.7，0.9)进行参数分析.图7给出了5种分数阶阶次影响下的隧道轴线处的地表沉降及其速率对比图.

由图7(a)可知,随着时间的推移,不同分数阶阶次下的地表沉降曲线趋势相同,均呈现出先陡后缓、最终趋向于一个定值的趋势,但最终沉降不同.α越大,土体固结过程越早完成.由图7(b)可知,随着时间的推移,不同分数阶阶次的速率曲线趋势相同,但在固结过程中曲线发生了交错.在固结初期,α越大,沉降速率越大;而在固结后期,α越大,沉降速率越小,但最终都趋向于零.