公里级激光反射层析实验和碎片质心估计*

张鑫源 胡以华† 谌诗洋 方佳节 王一程 刘一凡 韩飞‡

1) (国防科技大学,脉冲功率激光技术国家重点实验室,合肥 230037)

2) (国防科技大学,电子制约技术安徽省重点实验室,合肥 230037)

1 引言

随着航天活动的日益频繁,空间碎片与日俱增,对近地空间的航天器构成严重威胁.其中,尺寸为1—10 cm 的厘米级空间碎片,由于数目较多难以主动规避、预警,且尺寸较大被动防护实施困难,已经成为对在轨航天器威胁最大的空间碎片[1,2].目前,对于这类空间碎片清理的一种有效措施是大功率激光清理[3],其前提是空间碎片的精确定位和质心距离的高精度测量[4].其中,亚厘米甚至毫米级精度的质心探测是当今大功率激光清理技术的基础和关键之一.这是因为,大功率激光清理的工作原理是让强激光能量会聚于碎片质心,与碎片发生冲量耦合,使碎片获得一个速度增量,而冲量耦合必须作用于碎片的质心位置,才能使激光能量合理地与碎片发生作用,从而推动碎片移向大气层加以销毁,达到碎片清理的目的[5].当质心探测精度不足时,冲量耦合作用点偏离质心位置,碎片移动难以达到预期目标,无法实现空间碎片激光清理的目的.

厘米级空间碎片质心距离的高精度测量是亟待解决的世界性难题.迄今为止,卫星激光测距(satellite laser ranging,SLR)是单点测距精度最高的测量技术[6],对合作目标的测距精度能够达到亚厘米级[7,8].但是,对空间碎片这类非合作目标来说,由于能够返回接收机的回波强度受目标表面漫反射调制,测量难度远高于合作目标,实际测距精度仅达到分米级[9,10].此外,传统的空间碎片激光测距技术忽略了碎片表面形状对激光回波的调制[11],只是将其作为理想的点目标处理,实际探测过程中即使提高了激光测距系统的距离分辨率,也无法完成对厘米级空间碎片亚厘米级精度的质心探测.从现有探测技术来看,对厘米级空间碎片质心距离测量,主要依赖于光学或雷达图像[12-14],通过图像解算得到目标的质心位置.这类方法要求图像中碎片所占像素数不少于4 个,通过算法优化,最终可以达到的质心探测精度约0.5 个像素[15].但是,对于厘米级空间碎片来说,碎片在图像中应占据多个像素,在远距离情况下成像系统的单像素分辨率至少达到亚厘米级.比如,100 km 成像距离要求角分辨率达到0.1 µrad.传统光学和雷达成像手段从机理上难以达到上述精度要求.

激光反射层析技术(laser reflection tomography,LRT)是在计算机断层扫描(computed tomography,CT)基础上发展而来的新型成像探测技术,具有成像分辨率与距离无关的优势,且受外部环境因素影响较小[16].这项技术最早由Parker 等[17]于1988 年提出,以实际距离分辨率12.6 cm 实现了对10 m 处锥状目标横截面图像的重建工作.Matson等[18]利用HI-CLASS 相干探测激光雷达系统,以成像分辨率约0.2 m 实现了对915 km 高度处在轨LACE 卫星本体和伸缩臂上两个锗角反射镜的重构成像.Murray 等[19]开展了基于脉冲压缩的距离分辨LRT 实验,以成像分辨率15 cm 实现了对22.4 km 处直径1 m 的多个匀速旋转角反射器的重构成像.国内方面,Jin 等[20]以7.5 mm 的距离分辨率实现了对9.1 m 处长、宽、高分别为46 cm,41 cm,30 cm 的方形体的重构成像.Lin 等[21]首次将LRT 技术应用于平面目标质心探测,提出利用多角度回波数据解算质心距离的方法,以优于5 cm 的探测精度实现了对50 m 处目标(边长为141 cm × 70 cm、夹角45°的平面四边形)的质心定位.但是,对于形状复杂的空间碎片目标,由于遮挡效应的影响[22],某些角度存在不能被照射到的阴影区域,仅依靠多角度激光回波数据难以准确解算得到质心距离.目前,国内对LRT 的实验及其理论验证距离通常为10 m 到50 m[20,21,23].要实现千米级LRT 实验及其理论验证,进一步提高质心探测精度,要求激光器脉冲宽度更窄、高速探测电路带宽更大,同时发射系统参数与光学系统要高度匹配,对光路装调要求也较高.

为此,本文推导出三维目标实际投影的数学表达式,建立了厘米级空间碎片目标质心模型,并通过分析空间碎片目标与探测器的相对运动,提出了基于LRT 的厘米级空间碎片质心距离估计方法,开展了1 km 探测距离的实验验证.相比传统的空间碎片激光测距技术,本文实验使用的LRT 雷达样机具有更高的距离分辨率,且本文提出的质心估计方法考虑了碎片目标自身形状对回波波形的调制,实现了更高精度的质心探测,从机理上更具优势.该研究将厘米级空间碎片质心探测精度由1.50 cm 提高到0.34 cm,并实现了千米级LRT 实验及其理论验证的突破,将具有更广阔的应用前景和技术发展潜力.

2 LRT 原理与空间碎片质心模型

2.1 LRT 原理

LRT 的原理是将目标的一个切平面轮廓在多角度下进行反射投影[24],某角度下用平行激光束完全覆盖三维目标后得到该角度下包含目标表面反射分布信息的回波数据,并根据反射系数投影分布重建目标的二维截面图像.

探测过程如图1(a)所示,当准直激光束以ϕ角照射目标时,目标在该角度下的投影分布表示为

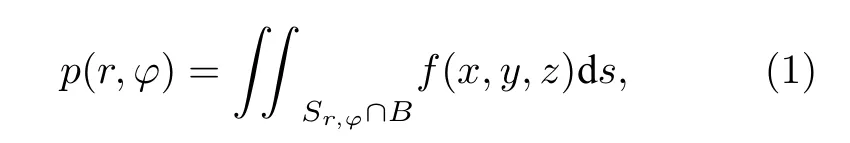
式中,Sr,ϕ为垂直于激光入射方向的平面,f(x,y,z)为目标的反射率分布,B为三维目标表面的点集.将图1(a)目标进行小面元分解,在z轴上分割出一系列小面元,每个小面元反射光强表示为

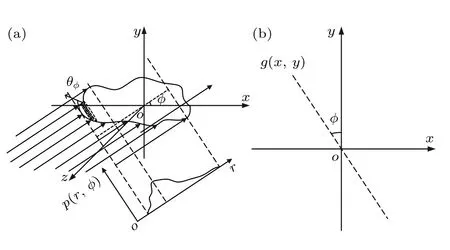
图1 LRT 示意图 (a) 目标投影;(b) 数据反投影Fig.1.Schematic diagram of LRT:(a) Target projection;(b) data back-projection.

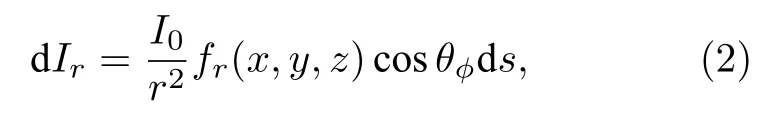
式中,I0是发射激光脉冲光强,r是探测距离,θϕ是小面元的法线与激光照射方向ϕ的夹角,fr(x,y,z) 是BRDF 函数.如果发射光束满足基模高斯条件,每个小面元反射光强表示为

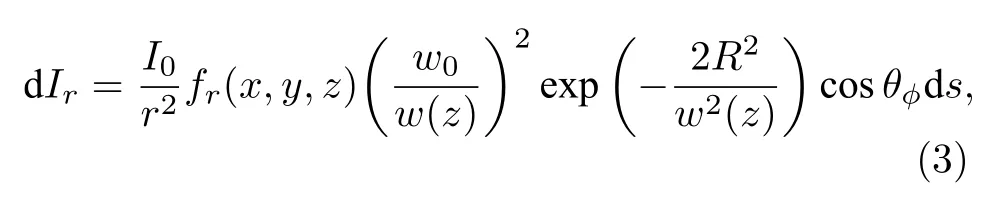
式中,w0是高斯光束的束腰半径,w(z) 是坐标z处的光斑半径.远场条件下,每个小面元反射光强表示为

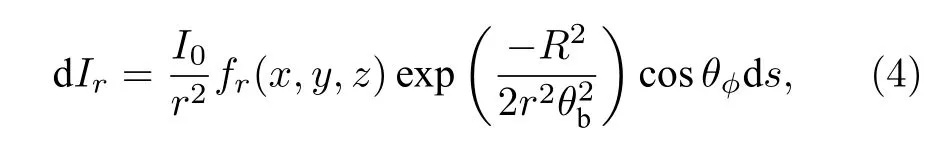
式中,R是面元到z轴的距离,θb是激光发散角.用距离r替代z,总反射光强表示为

式中,积分限表示积分在目标表面进行.根据以上分析,可以给出照射角度ϕ时目标反射系数投影分布的一般表达式如下:

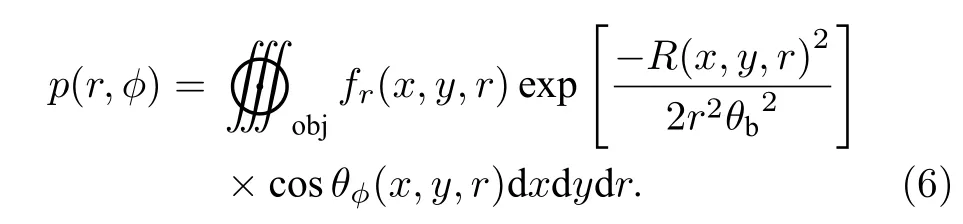
根据Lin 等[21]建立的回波卷积模型,回波可以表示为发射脉冲和目标反射系数投影分布的卷积:

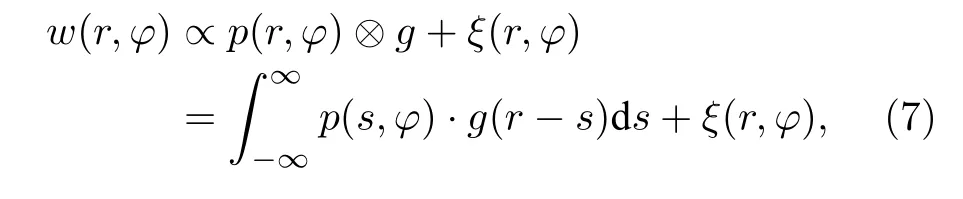
其中w(r,ϕ) 是照射角度ϕ的回波,g是入射脉冲波形,ξ(r,ϕ) 是加性噪声.

数据反投影示意图如图1(b)所示,在激光束照射区域内展开平行线,投影距离取决于激光照射区域的深度.值得注意的是,不同于X 射线能够穿透人体,激光束照射时无法穿透目标,因此反射率分布仅在目标表面是非零的.即f(x,y,z) 表示为

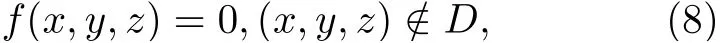
式中,D是目标表面的点集.根据傅里叶切片定理[25],投影数据的一维傅里叶变换F1(p(r,ϕ)) 和目标横截面吸收系数g(x,y) 的二维傅里叶变换F2(g(x,y)) 存在如下关系:

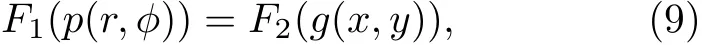
式中,F1,F2分别为一维和二维傅里叶变换.因此,获得目标全角度投影数据即可根据下式重建出目标的横截面图像:

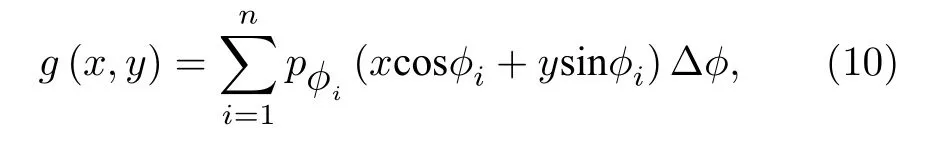
需要指出的是,g(x,y) 代表的是目标横截面反射系数分布函数,投影数据是指单探测器所获得的不同视角的激光反射回波信号并经离散采样后所得到的目标反射激光回波离散数据,重建出来的图像是目标横截面二维轮廓像.在实际成像过程中,LRT采用(10)式的离散投影数据来重建图像,并已证明由完全投影数据可以唯一重建图像.获取完全投影数据,就需要保证足够多的投影采样点,才能保证经过频域变换所得到的目标图像完整、精准.

2.2 基于LRT 的空间碎片目标质心模型

空间碎片根据形成原因可以有不同的形状,对于面状空间碎片目标,利用LRT 多角度回波数据直接解算质心距离的方法拥有较好的质心定位效果,且无需对全角度投影数据进行搜集[21].对于形状复杂的碎片目标,可以采用先成像后估计质心距离的方法.本文所讨论质心的概念,都是基于质量密度均匀的假设,并将目标看作是体积和形状不易发生改变的物体,即刚体.在此假设下,利用LRT技术进行精确重建目标几何结构,实现空间碎片目标质心坐标的精确解算.

典型空间碎片目标,如末级火箭筒、解体碎片、太阳能帆板等,平面或近似面状的薄层形状是其最常见的形状,且近似面状一般在一侧观测为凸面而另一侧观测为凹面.可以把它们简化成没有厚度的小的曲面元组合而成的组合面,其中小面元近似用平面元代替.基于密度均匀假设,假设面密度为ρ,针对目标形状分割为无限小面元 ds,质心坐标表示为

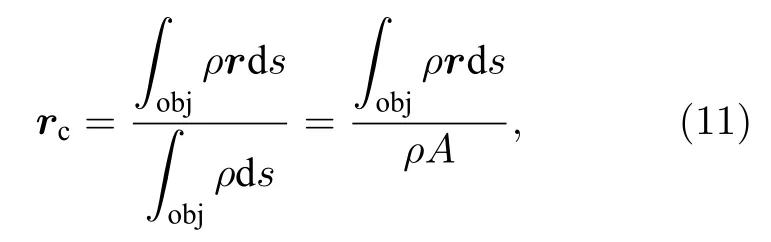
式中,rc是碎片质心笛卡尔坐标 (xc,yc,zc) 的矢量形式,积分限 o bj 表示积分在目标空间域内有效,A是目标的表面积.这说明要想解算目标的质心,必须知道其质量随距离的分布规律,常用的解算方法是利用图像法求解重构图像中质心的位置[21].灰度重心法可以看成以灰度为权值的加权型心法,灰度图像中目标的灰度重心 (x0,y0) 为

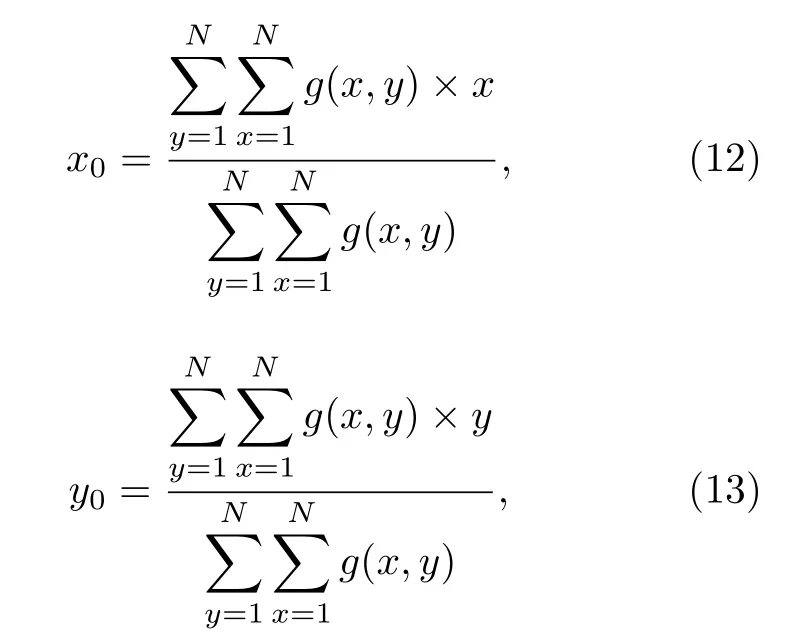
式中,g(i,j) 为像素点 (i,j) 处的灰度值,即权值.(i,j)为图像的两个方向,N是重构二维横截面图像g(x,y) 的尺寸.采用该方法处理密度均匀且为薄平面的空间碎片目标时,通常需要对图像进行阈值分割处理,将目标轮廓从背景中提取出来.这种方法能够较为准确地确定存在遮挡效应的复杂形状空间碎片目标的质心位置,通过二维横截面图像解算得到二维平面内的质心坐标后,结合本文提出的质心距离估计方法,即可确定质心距离.

3 系统构成与实验碎片模型

图2 所示为用于实现远距离空间碎片目标模型质心探测实验的LRT 雷达样机原理图,其关键参数如表1 所示.该LRT 雷达样机包括发射、接收、数据采集和数据处理4 个部分:发射部分由微片激光器、两个反射镜、一个分束棱镜、一个3 倍扩束镜和一个5—10 倍变倍激光扩束镜组成的扩束系统构成;接收部分采用望远系统接收,后接多模光纤输入APD 光探测模块;此外还有一个Pin光探测模块在消偏振分光棱镜另一侧用于记录参考信号;数据采集部分使用激光脉冲高速采集器;数据处理部分由工控机控制并完成实时数据处理.

图2 LRT 雷达样机原理图,其中 R 表示反射镜,NPBS 表示消偏振分光棱镜,APD 表示雪崩光电二极管,Pin 表示光电二极管,SMF 表示单模光纤,MC laser 表示微片激光器Fig.2.Schematic diagram of LRT radar prototype,where R is reflector,NPBS is non-polarizing beam splitter,APD is avalanche photodiode,Pin is positive intrinsic negative,SMF is single mode fiber,and MC laser is microchip laser.

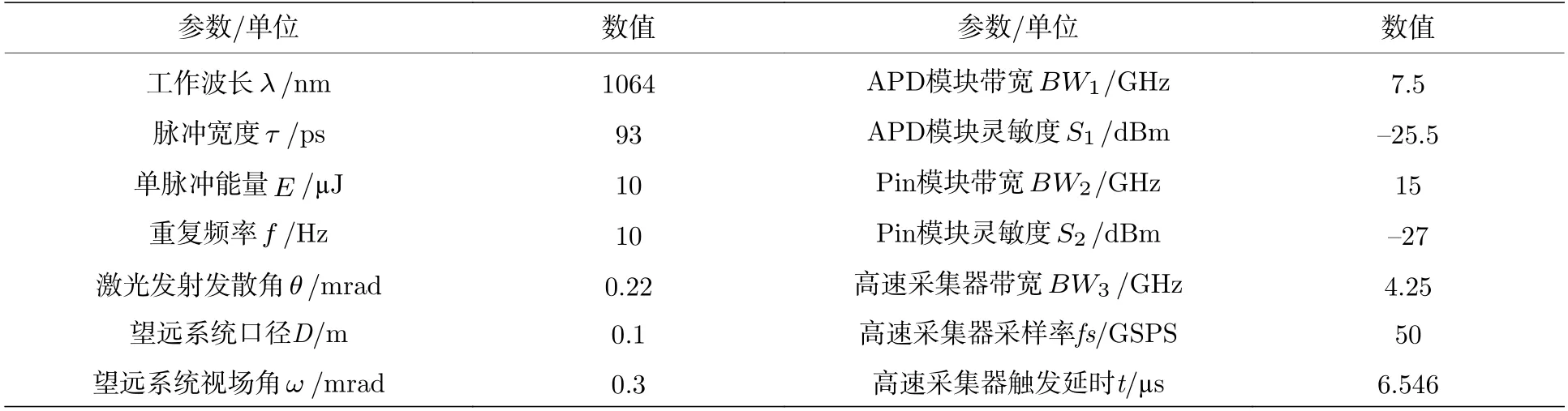
表1 LRT 雷达样机关键参数Table 1.Key parameters of the LRT radar prototype.

验证实验的探测距离为1 km.本实验使用的超短脉冲激光器采用半导体可饱和吸收体作为调Q开关,Nd:YVO4作为增益介质,直接键合到可饱和吸收体形成微片,谐振腔的长度在100 µm 量级,种子激光输出后经放大最终达到100 kW 以上的峰值功率.独特的设计、高精密制造以及智能化电源控制确保该激光器具有高电光转换效率、高光束质量、高可靠性等特点.微片激光器发出1064 nm脉冲激光后,经过一个可拆卸的倍频模块出射部分532 nm 绿光用于辅助调节光路,经过第一面反射镜后一路光经由消偏振分光棱镜进入Pin 光探测模块后由激光脉冲高速采集器通道一采集;另一路光通过分光棱镜后经由第二面反射镜入射扩束镜后照射到目标处并覆盖,经由目标表面调制后的回波被望远系统耦合进多模光纤内输入APD 光探测模块后,由激光脉冲高速采集器通道二采集;通道一采集的发射信号作为参考,触发后延时开始采集通道二的信号.为保证远距离处光斑完全覆盖目标,采用650—1300 mm 变焦望远镜和CCD 相机组成系统在发射端对远处目标进行成像,调节发射激光俯仰、方位,直到光斑完全覆盖目标.

数据处理部分应用的算法就是本文提出的质心距离估计方法,工控机控制采集到多角度激光回波数据后,先进行数据预处理,分析得到其峰值点距离变化规律和转动周期,将多个周期回波数据整合排列后,取峰值点距离的平均值作为质心距离的初始估计.然后,利用凸面对应的180°的回波数据进行滤波反投影(filtered back projection,FBP)重构,获得目标横截面二维轮廓像.接着,对重构图像进行图像处理,解算得到质心确定结果,并结合理论质心对初始质心距离估计进行校正,利用校正后的质心再次进行FBP 重构,循环此过程,直到解算得到的质心确定结果与理论质心的距离小于一个像素对应的最小可校正误差时终止.

构建由三个边长为5 cm、两两夹角135°的正方形组合而成的近似面状结构作为典型空间碎片目标模型,如图3(a)所示.图示坐标系原点o选取在碎片质心处,探测过程中碎片目标所在xoy平面绕oz轴转动,规定沿ox轴正向时的激光束照射角度ϕ为0°.遮挡效应示意图如图3(b)所示,激光束照射角度ϕ存在不能照射到的阴影区域,该角度激光回波数据仅受到黑色标记区域目标表面的调制,缺失了红色标记区域的目标表面信息,该角度回波难以准确解算得到质心距离.因此如何利用多角度激光回波反演得到目标完整、精准的轮廓图像从而准确解算得到质心距离成为本文研究的关键点.

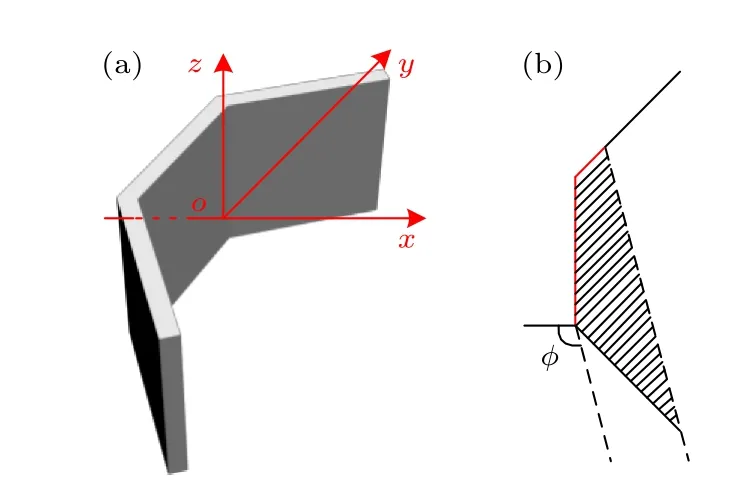
图3 典型空间碎片模型 (a)结构示意图;(b)遮挡效应示意图Fig.3.Typical space debris model:(a) Structure diagram;(b) diagram of shielding effect.

4 1 km 实验结果与质心距离估计

图4(a)给出了上述LRT 雷达样机实验装置图,利用该样机在合肥董铺水库大坝上对图3(a)所示的典型空间碎片目标模型开展1 km 距离的LRT 质心探测实验,实验示意图如图4(b)所示.激光光斑在1 km 处直径约22 cm,接收光学系统1 km 处视场约30 cm,接收光学系统视场能够覆盖到激光束.

图4 (a) 实验装置图;(b) 1 km 实验验证示意图Fig.4.(a) Diagram of the experimental set-up;(b) diagram of 1 km experiment verification.

厘米级空间碎片目标质心探测的难点在于,对于作为非合作目标的空间碎片来说,如果需要考虑其自身形状对回波波形的调制,就需要利用多角度激光回波反演得到目标完整、精准的轮廓图像.结合地基或天基平台测得的空间碎片目标轨道参数和探测器轨道参数,建立碎片与探测器的相对运动模型,能够实时校正空间碎片目标与探测器的距离.空间碎片目标通常围绕其质心高速转动[26].校正后的相对运动可以看作是探测器固定,空间碎片目标围绕自身质心作匀速转动,而其作为非合作目标,转动周期是未知的.因此,首先需要从足够多的回波波形采样数据中,确定空间碎片目标的转动周期.选取采样间隔7°等间隔采样得到的500 组多角度激光回波波形如图5 所示.需要指出的是,工控机控制采集开始的触发延时为6.546 µs,图中原点处对应的探测距离为981.9 m,计算距离时需要加上延时对应的距离值.提取各角度回波对应的峰值点距离如图5 中红色折线b 所示,可以看到峰值点距离存在很多异常值,这是因为某些角度采集得到的回波信噪比较差,波形湮没在噪声中.利用差分过滤方式将异常值去除,本文设置阈值为0.015 m 和—0.015 m,只有前一个差分值和后一个差分值是一正一负或一负一正的情况才判断为异常值并删除,剩余的峰值点距离利用插值方式获得的折线图如图5 中蓝色折线a 所示.选取相邻极值点对应角度分别为721°和1078°,与多角度激光回波共同确定转动周期T,确定的周期共包含357°,与转动一周对应的360°大致相同.

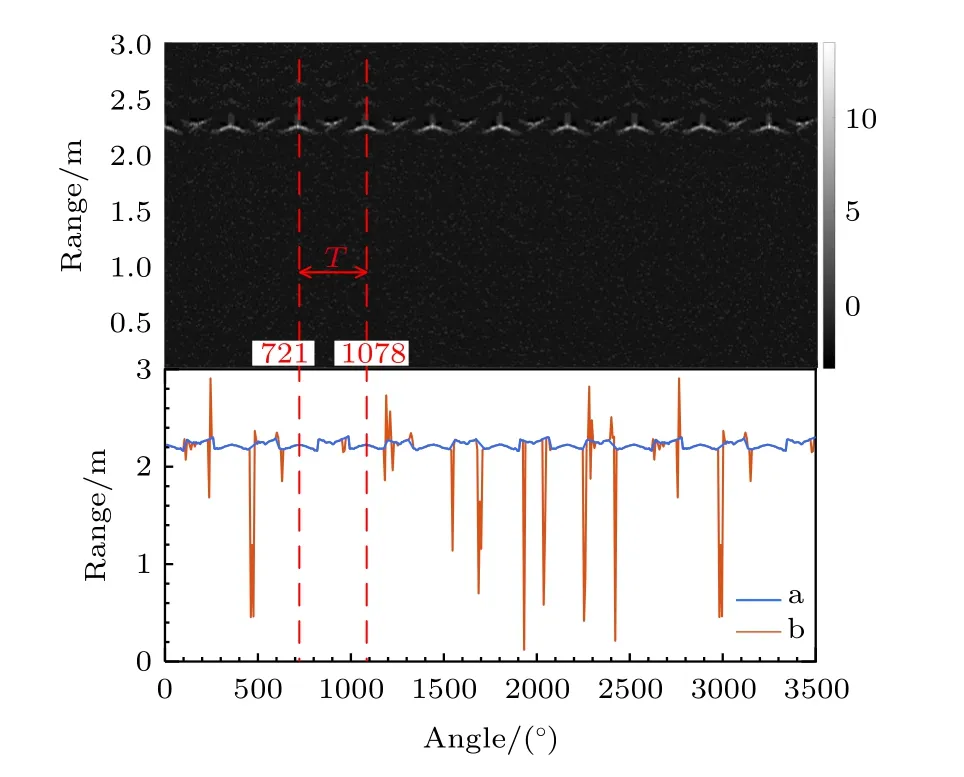
图5 多角度激光回波和峰值点距离确定转动周期Fig.5.Multi-angle laser echoes and the peak point range determined the period of rotation.

确定空间碎片转动周期后,可以确定一个周期内采集到的回波数目,例如图5 所示的一个周期包含51 组回波数据,将相邻周期采集到的回波数据依次补全到该周期采集到的回波数据的间隙,补全后得到转动一周内等效为采样间隔1°对应的全角度激光回波波形数据,如图6 所示.分析其峰值点距离发现最大值为2.352 m,而最小值为2.160 m,也就是说仅依靠单角度回波确定的质心距离误差最大可以达到19.2 cm;利用多角度回波数据解算质心距离的方法,根据平面状目标质心探测公式[21]

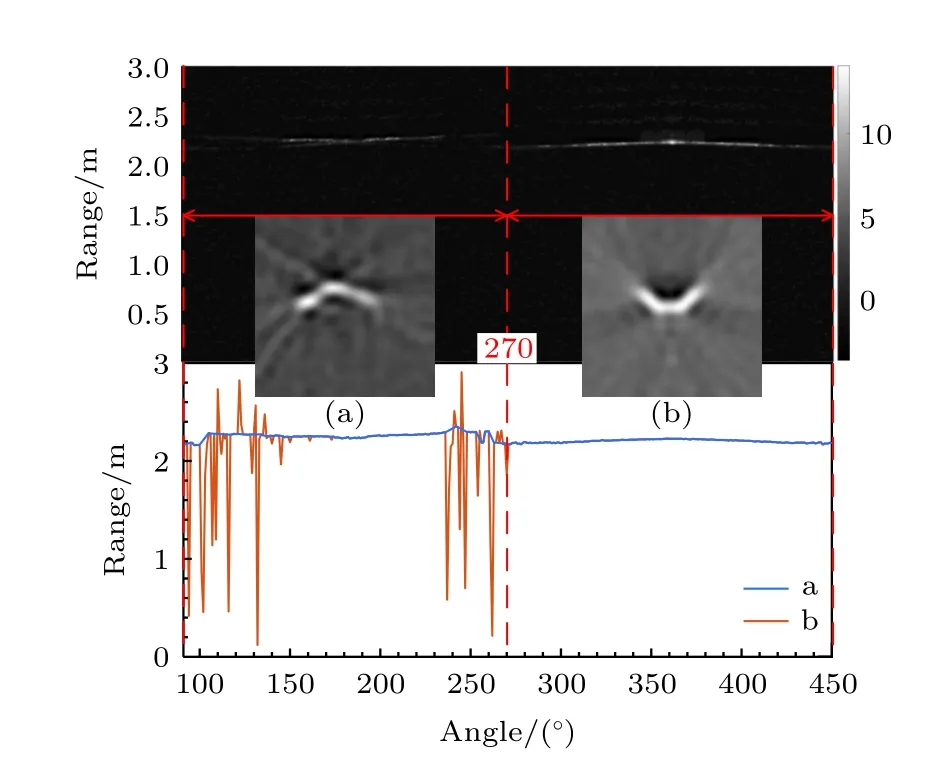
图6 补全后的多角度激光回波和目标重构图像 (a) 凹面对应回波数据的FBP 重构图像;(b) 凸面对应回波数据的FBP 重构图像Fig.6.Multi-angle laser echoes after completion and reconstructed image of target:(a) Image reconstruction by FBP based on the echo data of concave surface;(b) image reconstruction by FBP based on the echo data of convex surface.

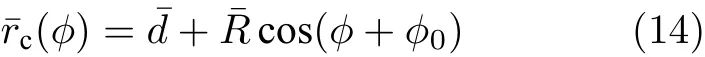
得到的质心距离为2.250 m,计算得到的质心距离与实际值的误差为1.50 cm,这种方法忽略了目标表面遮挡效应的影响,从机理上无法满足质心距离高精度测量的需要,难以实现针对非平面状厘米级空间碎片亚厘米级甚至毫米级的质心距离测量.

图6 所示是补全后等效为采样间隔1°对应的全角度激光回波,提取各角度回波对应的峰值点距离如图6 中红色折线b 所示,利用差分法去除异常值后插值得到的折线如图5 中蓝色折线a 所示.可以看到,折线明显存在两个突变值,这是由于近似面状的碎片目标在一侧观测为凸面而另一侧观测为凹面,由凹面到凸面或凸面到凹面转动时,回波波形对应的峰值点距离会发生突变,图5 所示91°—270°对应的回波数据是凹面,271°—450°对应的回波数据是凸面,分别对凹面和凸面对应的回波数据进行FBP 重构,所得目标重构图像如图5(a),(b)所示.由于碎片目标与探测器的相对运动被认为是围绕其自身质心的转动,因此重构过程中碎片目标的旋转中心用质心代替,而质心距离的初始估计为蓝色折线a 对应峰值点距离的平均值.比较目标重构图像不难看出,凸面对应的回波数据获得的重构图像轮廓更清晰,这是由于凹面受遮挡效应影响明显强于凸面,因此后续对质心距离的校正采用凸面对应的回波数据获得的目标重构图像处理完成.

利用补全后的凸面对应的回波数据进行FBP重构,质心距离校正前后的FBP 重构图像如图7(a),(b)所示,采样间隔为1°.分别对FBP 重构图像进行阈值分割处理,得到如图7(c),(d)所示的阈值分割图像.在阈值分割图像中用方形标记质心确定结果,并用圆形标记理论质心.

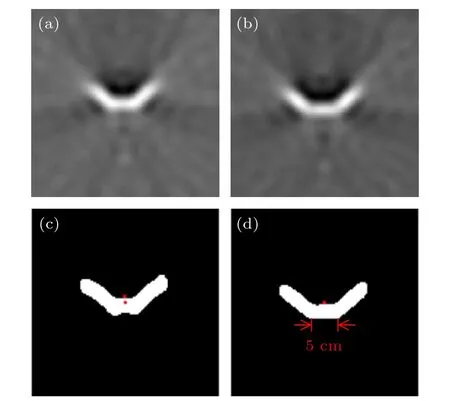
图7 采样间隔1°的目标重构图像与质心确定结果.FBP 重构图像 (a) 质心距离校正前;(b) 质心距离校正后.阈值分割图像 (c) 质心距离校正前;(d) 质心距离校正后Fig.7.Target reconstruction image with sampling interval of 1° and barycenter determination results.Image reconstruction by FBP:(a) Barycenter range before correction;(b) barycenter range after corrected.Threshold segmentation image:(c) Barycenter range before correction;(d) barycenter range after corrected.

根据(12) 式和(13)式计算得到图7(c)中质心坐标为(63.9735,60.2458),用方形标记;而理论质心坐标为(64.5000,64.5000),用圆形标记.计算得到二者相距4.2867 个像素,根据1 个像素对应0.3 cm 的转换关系,得到质心确定结果与理论质心之间的距离为1.29 cm,即质心确定误差的确定值为1.29 cm.需要指出的是,最终计算质心距离时需要加上工控机控制的触发延时对应的探测距离981.9 m,为便于分析这部分数据均采用未加上该距离的数值.利用该误差对质心距离进行校正,重新进行FBP 重构得到图7(d)所示校正后的阈值分割图像,可以看到此时质心确定结果与理论质心十分接近,根据(12) 式和(13)式计算得到质心坐标为(64.5293,64.0195),转换得到此时的质心确定误差的确定值为0.14 cm.此外,校正后的图像轮廓也更接近真实的碎片目标轮廓,在图上标示出5 cm 对应的像素值发现,重构轮廓尺寸与目标尺寸基本一致.校正前后质心距离和质心确定误差结果比较如表2 所示,校正后质心距离与实际值误差仅为0.34 cm,达到了毫米级质心探测精度的要求.

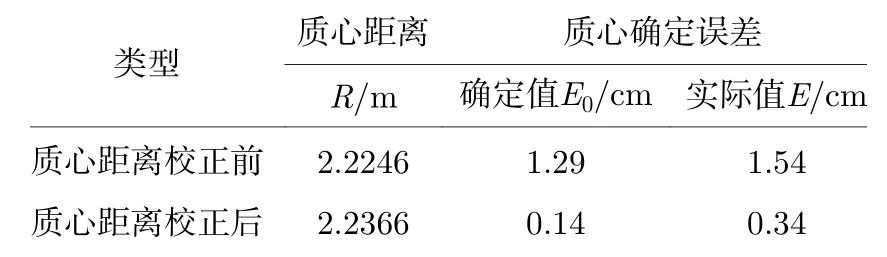
表2 采样间隔1°的目标重构图像校正前后质心距离和质心确定误差结果比较Table 2.Comparison of barycenter range and determination error before or after target reconstruction image correction with sampling interval of 1°.

分析计算能够重构图像的最大采样间隔,假设截止频率为umax,目标空域最大尺寸为Dmax,根据耐奎斯特采样定律,频率间隔要小于才能完全重建出目标图像,可得到角度间隔Δϕ的采样限制条件为[27]

截止频率umax可以通过激光脉冲和探测器确定的距离分辨率计算得出.这里,可以认为相较于探测电路的响应时间,激光脉冲确定的距离分辨率较低,距离分辨率 ΔR转换傅里叶频域得:

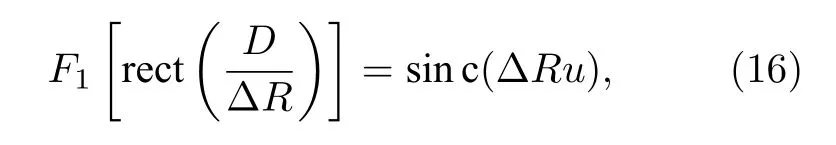
设 s in c 函数第一个频域零点为目标图像频域截止频域,根据距离分辨率 ΔR和脉冲宽度τ的关系式ΔR=,可以得到单个投影上反射层析投影采样角度数Nϕ的限制条件为

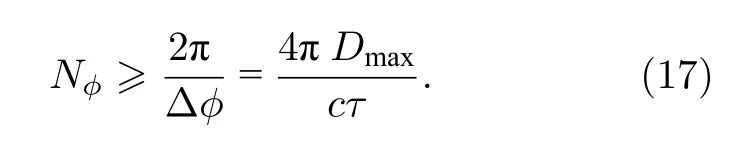
根据(17)式计算得到的最大采样间隔为6.6°,选取采样间隔7°时凸面对应的激光回波数据共25 组进行FBP 重构,得到质心距离校正前、质心距离第一次校正后和质心距离第二次校正后的FBP重构图像如图8(a)—(c)所示,可以看到采样间隔增大后目标重构图像中的伪影和噪点明显增加.

校正前后质心距离和质心确定误差结果比较如表3 所示,图8(d)中质心确定结果与理论质心之间的距离为2.43 cm.利用该误差对质心距离进行第一次校正,重新进行FBP 重构,得到图8(e)所示校正后的阈值分割图像,此时质心确定误差的确定值为0.39 cm.然后,进一步对质心距离进行第二次校正,进行FBP 重构,得到图8(f)所示的阈值分割图像,此时质心确定结果与理论质心十分接近,质心确定误差的确定值为0.22 cm,小于一个像素对应的0.3 cm 的最小可校正误差.因此校正循环终止,此时的图像轮廓与真实的碎片目标轮廓接近,且经过两次校正后质心距离与实际值误差仅为0.50 cm,达到了毫米级质心探测精度的要求.

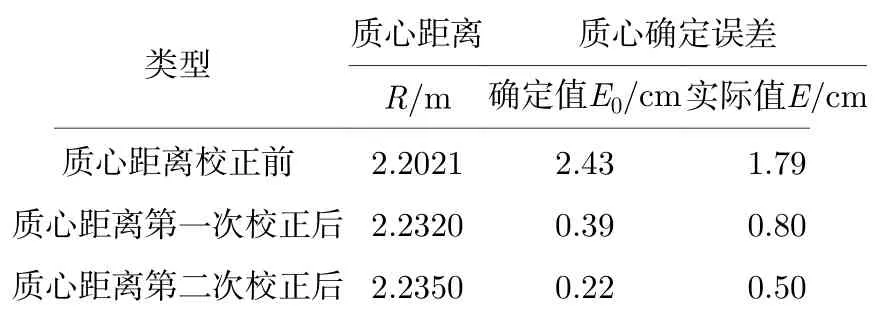
表3 采样间隔7°的目标重构图像校正前后的质心距离和质心确定误差结果比较Table 3.Comparison of barycenter range and determination error before or after target reconstruction image correction with sampling interval of 7°.

进一步探讨稀疏角度采样环境下的质心距离解算效果,选取采样间隔20°时凸面对应的激光回波数据共9 组,进行FBP 重构,得到质心距离校正前后FBP 重构图像如图9(a),(b)所示,可以看到稀疏角度采样环境下目标重构图像存在大量伪影且目标轮廓与真实轮廓存在偏差.

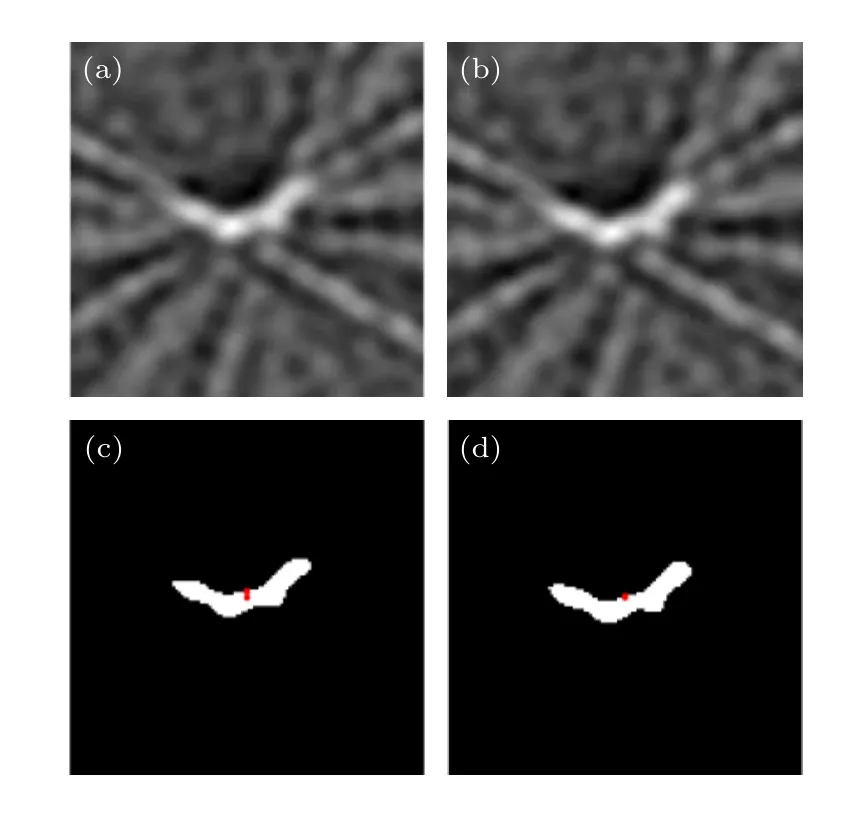
图9 采样间隔20°的目标重构图像与质心确定结果.FBP 重构图像 (a) 质心距离校正前;(b) 质心距离校正后.阈值分割图像;(c) 质心距离校正前;(d) 质心距离校正后Fig.9.Target reconstruction image with sampling interval of 20° and barycenter determination results.Image reconstruction by FBP:(a) Barycenter range before correction;(b) barycenter range after corrected.Threshold segmentation image:(c) Barycenter range before correction;(d) barycenter range after corrected.

校正前后质心距离和质心确定误差结果比较如表4 所示,图9(c)中质心确定结果与理论质心相距0.70 cm,利用该误差对质心距离进行校正,重新进行FBP 重构得到图9(d)所示校正后的阈值分割图像.此时,质心确定误差的确定值为0.15 cm,而实际值为1.70 cm,证明该方法应用于稀疏角度采样环境下也能够实现超过2 cm 探测精度的质心距离解算.

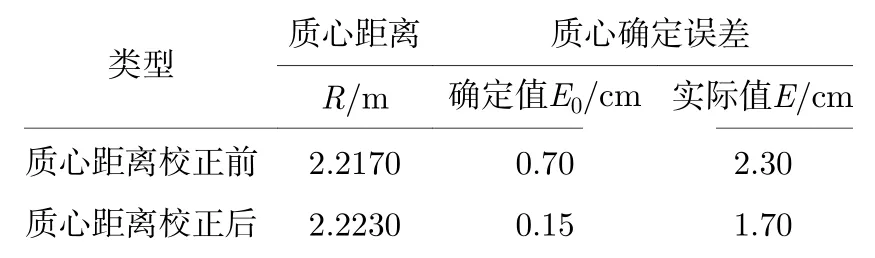
表4 采样间隔20°的目标重构图像校正前后质心距离和质心确定误差结果比较Table 4.Comparison of barycenter range and determination error before or after target reconstruction image correction with sampling interval of 20°.

在稀疏角度采样的环境下,本文使用FBP 算法对目标图像进行重构,难以精准重建出目标轮廓.随着压缩感知(compressed sensing,CS)理论的提出,可以运用更多新的图像重建算法和图像后处理方法,提升重建图像质量[28,29].根据CS 理论,图像迭代重建增加关于稀疏变换后图像的稀疏性约束,可以解决稀疏角度和有限角度回波数据精确重建问题[30],为基于LRT 的厘米级空间碎片质心距离估计方法提供了更大的应用前景.

5 结论

本文结合LRT 原理建立了厘米级空间碎片目标质心模型,提出了质心距离估计方法.通过对LRT 雷达样机关键部件参数进行优化设计及对系统的高精度装调,成功研制了用于实现远距离质心探测实验的LRT 雷达样机,并针对典型厘米级空间碎片目标模型开展了1 km 探测距离的实验验证.实验结果表明,针对由三个边长为5 cm、两两夹角135°的正方形组合而成的近似面状结构的典型厘米级空间碎片目标模型,该方法的质心探测精度能够达到0.34 cm,且在稀疏角度采样的环境下,也可以实现1.70 cm 探测精度的质心距离解算.

展望未来,随着CS 理论的提出,可以运用更多新算法来提升重建图像质量,进一步提高该方法的质心探测精度.结合LRT 技术具有成像分辨率与距离无关的优势,在可以预见的将来就能实现百公里级LRT 空间碎片质心探测,届时亚厘米级甚至毫米级的质心探测精度将远远优于传统光学或雷达成像技术通过图像解算得到目标质心位置的精度,同时对数百千米距离大功率激光清理空间碎片也将具有一定指导意义.

感谢合肥市董铺·大房郢水库管理处对本文实验的大力支持与帮助.