具有异质增益因子的超图上的演化公共品博弈*
2022-06-18陈蔚颖潘建臣韩文臣黄昌巍3
陈蔚颖 潘建臣 韩文臣 黄昌巍3)†
1) (广西大学计算机与电子信息学院,南宁 530004)
2) (四川师范大学物理与电子工程学院,成都 610101)
3) (广西大学,广西多媒体通信与网络技术重点实验室,南宁 530004)
1 引言
利他(合作)行为广泛存在于自然界和人类社会[1].然而,根据达尔文自然选择理论,理性个体在面临个人利益和群体利益的两难选择冲突困境时,个体将会选择能够最大化自身利益的利己(背叛)行为.社会困境中自私个体合作行为的自发涌现和维持吸引了物理、数学、生物和信息等领域研究学者的广泛关注,博弈理论被发现能够为解释群体中合作行为的涌现和维持背后的机制提供强有力的理论框架.在经典演化博弈理论中,通常假设群体中的个体以相同的概率进行接触并发生相互作用.通过平均场理论分析发现,囚徒困境博弈情境下合作行为无法在充分混合群体中存在[2].然而,Nowak 和May[3]考虑具有空间结构的网络上进行演化博弈的开创性研究工作表明,群体中的合作者能够自发地形成紧凑的合作团簇,从而抵御背叛者的入侵,合作行为通过网络互惠机制得到了促进.此后,伴随着网络科学的蓬勃发展,复杂网络上的演化博弈吸引了国内外学者的广泛关注和研究[4-6].
作为经典多人博弈模型,公共品博弈是刻画多人囚徒困境博弈最常用的模型.目前,学者们对复杂网络上的演化公共品博弈进行了大量的研究.一方面,已有很多研究工作关注于复杂网络拓扑结构对于空间公共品博弈中合作演化的影响.例如,Santos 等[7]探究了BA 无标度网络上的演化公共品博弈,对比规则网络上公共品博弈的合作演化结果,网络异质性进一步增强了公共品博弈中合作行为的涌现;Rong 和Wu[8]研究了无标度网络上节点度的相关性对公共品博弈中合作演化的影响;Battiston 等[9]讨论了多层网络上的公共品博弈中各层网络重叠程度和增益因子对群体合作演化的影响;Huang 等[10]考虑了具有非对称相互作用和策略学习环境的双层网络上的公共品博弈,研究发现,相互作用网络和策略学习网络的重叠边比例会显著影响群体中的合作行为.另一方面,为理解公共品博弈困境下群体合作行为的涌现机制,各种促进公共品博弈中合作涌现的具体机制被提出并得到了广泛研究.包括奖励与惩罚机制[11-16]、异质投资[17,18]、排斥策略[19,20]、个体迁移[21]、容忍策略[22,23]、从众机制[24]、收益再分配[25]等.此外,异质增益因子对公共品博弈中合作演化的影响同样受到了关注.Shi 等[26,27]探究了方格子网络上公共品博弈中异质增益因子对群体合作演化的影响,发现异质群体增益因子的引入对群体合作行为的涌现具有促进作用.Chen 等[28]和Weng 等[29]讨论了随时间改变的异质增益因子对公共品博弈中合作演化的影响,他们发现动态变化的增益因子能够显著地提高群体合作水平.
上述研究工作都是基于普通图上的空间公共品博弈讨论群体的合作演化,而普通图中的连边通常只能表征节点两两之间的相互作用关系.随着社会经济和信息技术的快速发展,现实生活中社会成员及群体之间的关系表现出了越来越复杂和多元化的特点,考虑到普通图在刻画个体间相互作用关系上的局限性,能够更好描述个体之间复杂多元关系的超图模型得到了越来越多学者的关注[30-33].最近,Burgio 等[34]探究了高阶相互作用下群体的合作演化.Alvarez-Rodriguez 等[35]较为系统地研究了具有不同网络拓扑特征的超图上的公共品博弈,并通过科技论文合作者实证数据分析了群体合作如何依赖于群体规模.受到以上研究工作的启发,本文构建了引入异质增益因子的超图上的演化公共品博弈模型.基于均匀随机超图,研究了不同网络阶数对具有特定增益因子分布的公共品博弈中合作演化的影响.我们发现,特定增益因子分布的均匀超图上的公共品博弈中网络阶数的增大能够促进群体合作行为的涌现.进一步地,本文探究了给定阶数的均匀超图中服从不同分布的异质增益因子对群体合作行为的影响.最后,讨论了超图上不同超边数目对系统合作演化的影响.
2 超图上具有异质增益因子的公共品博弈模型
不同于普通图上一条边只能连接两个节点,超图上的边(又称为超边)可以连接不少于 2 的任意数量的节点.每条超边连接的节点数量都相同且为g的超图称为g阶超图,当g=2 时超图即退化为普通图.基于Alvarez-Rodriguez 等[35]的研究工作,我们建立了g阶超图上的演化公共品博弈模型.超图上的节点表征博弈个体,个体之间的相互作用关系通过超边进行刻画.初始时,群体中个体随机选择采取合作或背叛策略.在每个时间步,采取合作策略的个体(合作者)将在所参与的博弈群组单元进行的公共品博弈中做出一个投资c(不失一般性,设定c=1),而采取背叛策略的个体(背叛者)将不会做出任何的投资.在一个博弈群组单元中所有合作者的投资总和将会乘以增益因子R,然后再均分给该博弈群组单元中的所有个体.在g阶均匀随机超图上,基本博弈群组单元规模为g.因此,在由g个个体组成的博弈群组单元公共品博弈中,合作者和背叛者获得的收益可以分别表示为πC=RcwC/g-c和πD=RcwC/g,其中wC为该博弈群组单元中合作者的数目,R为增益因子.
与普通图上的空间公共品博弈不同,超图上的空间公共品博弈以超边内个体组成的群组作为基本博弈群组单元.本模型考虑超图上的节点规模为N=1000,超边数目为L.对于均匀随机超图,存在临界超边数目Lc=(N/g)lnN使得超图全连通.为保证超图的连通性,L≥Lc.系统根据包含以下基本步骤的标准蒙特卡罗模拟过程进行演化.首先,从整个群体中随机选择一个个体i以及该个体所在的一条超边li,j(即包含i个体的第j条超边),超边中所有个体参与他们各自所在的所有超边中个体组成的基本博弈群组单元里的公共品博弈并累积收益.如图1所示,以 9 个节点和 4 条超边构成的 3 阶均匀超图为例,假设从群体中随机选择的一个个体i为n3,同时随机选择了n3所在的一条超边l2,超边l2中的所有个体要参与他们各自所在的每条超边中个体构成的博弈群组中的公共品博弈,即n3将参与其所在的l1和l2群组中的公共品博弈,n4将参与其所在的l2群组中的公共品博弈,n5将参与其所在的l2,l3以及l4群组中的公共品博弈.超边li,j中个体i的累积收益表示为
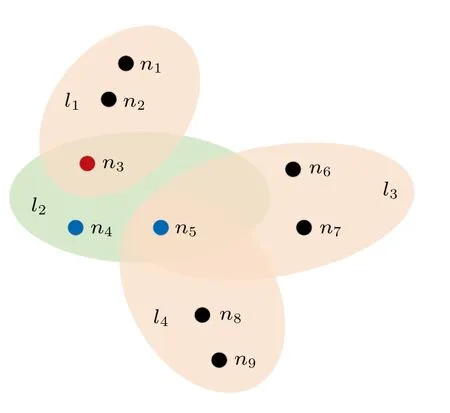
图1 3 阶均匀随机超图上的空间公共品博弈Fig.1.The spatial public goods game on uniform random hypergraph with hyperlinks of order equal to g=3.

其中,ki为节点i的超度,个体i参与其所在的第h条超边中个体组成的博弈群组的公共品博弈获得的收益表示为

其中,Δ为整个群体中个体之间可能的最大收益差的绝对值.N次包含上述两个基本步骤的演化过程,构成一个完整的蒙特卡罗模拟过程,即在一个蒙特卡罗时间步中,平均每个个体具有一次更新自身策略的机会.
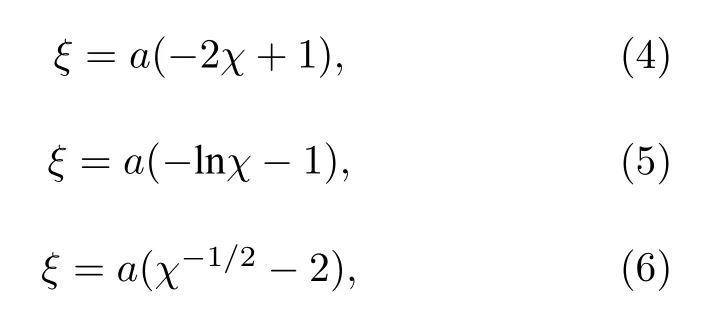
其中参数a为函数ξ的振幅(a=0,系统回到原始模型,博弈群组增益因子都为r0),上述3 种分布中的χ都是服从 [0,1] 均匀分布的一个随机数,并且这保证了整个群体中ξ的均值为0.因此,服从上述3 种不同分布的都满足关系式=r0,即博弈群组单元异质增益因子的均值都相同并且为r0.原始和a=1 时ξ服从上述3 种特殊分布的超边数目为L=500 的超图上的空间公共品博弈中,不同超边对应的博弈群组的增益因子分布情况如图 2 所示,可以看到,原始模型中所有博弈群组的增益因子都相同,ξ为幂律分布时对应的群体中增益因子的异质性最强(即少数超边对应的博弈群组的增益因子非常大,而大多数超边对应的博弈群组的增益因子很小),ξ为均匀分布时引起的增益因子异质性在除原始模型外的3 种特殊分布中最弱,指数分布介于幂律分布和均匀分布之间.

图2 r0=1.0 和 a=1.0 时4 种分布情况下的群体增益因子 rl=r0(1+ξ) 的分布 (a) 原始模型;(b) 均匀分布;(c) 指数分布;(d) 幂律分布Fig.2.Distributions of synergy factors rl=r0(1+ξ) for r0=1.0and a=1.0 of the four cases:(a) Original model;(b) uniform distribution;(c) exponential distribution;(d) power-law distribution.
3 数值模拟结果与分析
本节对上述g阶均匀超图上的空间公共品博弈模型进行蒙特卡罗模拟,讨论和分析网络阶数g和不同增益因子分布模式对超图上空间公共品博弈中合作演化的影响.群体合作水平fC定义为fC=NC/N,其中N和NC分别代表博弈群体总人数和群体中采取合作策略的人数.超图节点规模为N=1000,除特别标注外,超图上的超边数目为L=Lc=(N/g)lnN.3 种异质分布的振幅取值为a=1.特定参数下系统的演化结果都是系统在经过足够长的演化时间进入稳定状态后并通过不少于 10 次不同初始条件下系综平均得到的结果.
图3 给出了包含原始经典模型在内的4 种增益因子分布情况下,不同阶数g的超图上的群体合作水平fC随增益因子均值r0的变化情况.定义临界增益因子均值rc,即群体合作水平fC=0.5 时对应的r0值.r0≥rc时群体中合作策略占主导,而r0<rc时群体中背叛策略占主导.从图 3 可以看到,无论是在具有同质增益因子的超图上的公共品博弈(原始模型)中,或是在增益因子服从均匀分布、指数分布和幂律分布的超图上的公共品博弈中,任意g值下系统的合作水平fC都随增益因子均值r0的增大而增大.此外,在上述任意一种给定增益因子分布的空间公共品博弈中,临界增益因子阈值rc随着超图阶数g的增大而减小.并且,随着博弈群组增益因子异质性的增强(如增益因子服从幂律分布时),超图阶数g值的增大对合作的促进作用越显著.由于以上结果是基于超边数目为L=Lc=(N/g)lnN的超图上的公共品博弈得到的演化结果,随着g的减小,超图上超边的数目将增大.而超图连边变得更为稠密,将使得超图上的博弈群体趋向于完全混合的情况,不利于群体中合作行为的涌现.
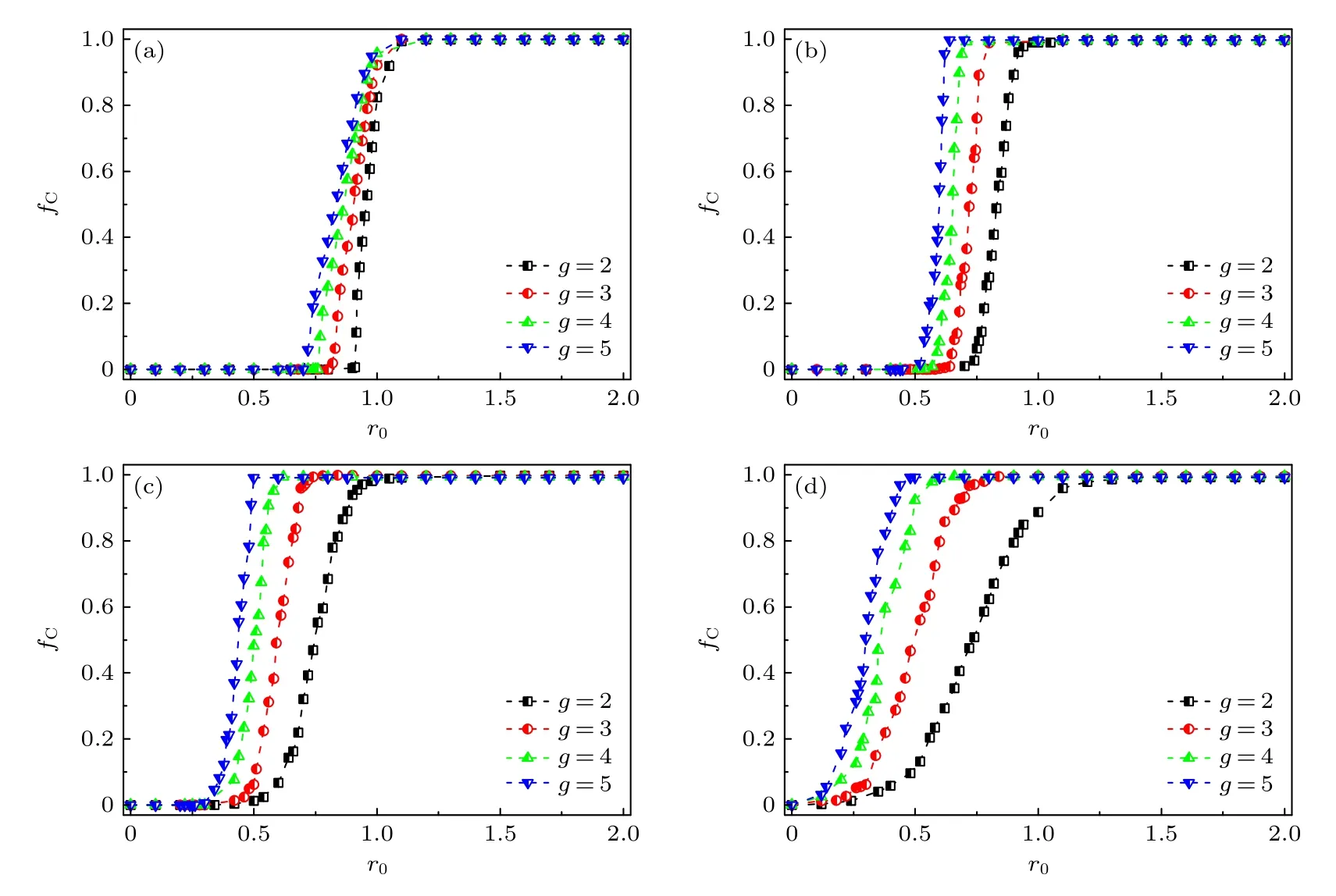
图3 4 种增益因子分布情况下,不同阶数 g 的超图上群体合作水平 fC 随 r0 的变化 (a) 原始模型;(b) 均匀分布;(c) 指数分布;(d) 幂律分布Fig.3.Fraction of cooperators fC as a function of r0 for hypergraphs with different orders g :(a) Original model;(b) uniform distribution;(c) exponential distribution;(d) power-law distribution.
进一步地,为更加直观地展示超图上不同增益因子分布模式对群体合作演化的影响,在图 4中给出了阶数g分别为2,3,4 和5 时的均匀超图上具有不同增益因子分布模式的空间公共品博弈中群体合作水平随增益因子均值r0的变化情况.从图 4可以看到,随着r0逐步增大,系统合作水平从 0 单调增大到 1 .同时,在确定阶数的均匀超图上,具有越强博弈群组增益因子异质性的群体中合作策略占主导地位对应的临界增益因子均值rc越小.相对于博弈群组增益因子都相同的原始模型上的演化结果,在r0较小时,博弈群组增益因子的异质性能够极大地促进群体的合作行为.尤其是在阶数g比较大的超图上,异质增益因子能够显著地提高系统的合作水平,博弈群组增益因子的异质性越强越有利于博弈群体中合作行为的涌现.

图4 不同超图阶数 g 值情况下,4 种增益因子分布对应的群体合作水平 fC 随 r0 的变化 (a) g=2 ;(b) g=3 ;(c) g=4 ;(d)g=5Fig.4.Fraction of cooperators fC as a function of r0 on hypergraphs with (a) g=2,(b) g=3,(c) g=4 and (d) g=5 for the four situations.
在具有异质增益因子的博弈群体中,由于博弈群组增益因子的不均匀性,群体中部分博弈群组将具有较大的增益因子.参与具有较大增益因子的博弈群组公共品博弈的个体将更倾向于采取合作策略,从而更容易形成稳定的合作团簇.尤其是在增益因子服从异质性最强的幂律分布情况下,即使在增益因子均值r0比较小时,也能够使得群体中产生部分增益因子很大的博弈群组.该部分博弈群组的存在,将极大促进群体中合作行为的涌现和维持.图 5 给出了r0=0.35 时 5 阶均匀超图上空间公共品博弈演化到稳态时群体中各个博弈群组单元中合作者数目wC的分布情况.可以看到,对于原始模型或增益因子异质性比较弱的均匀分布情况,所有博弈群组中合作者数目都为 0,群体中个体无法维持合作行为.而在异质性比较强的指数分布情况下,能够存在少数博弈群组,群组中部分个体依然能够维持合作策略.另外,在异质性更强的幂律分布情况下,多数群组中能够存在一定数目的合作者,甚至出现了较高比例的wC=5 的博弈群组,即群组中个体都采取合作策略.上述4 种分布中,博弈群组增益因子均值都为r0=0.35 .在原始模型中,群体中所有群组的增益因子都为r0,这种情况下,任何一个博弈群组都无法维持合作行为.而在幂律分布情况下,群体中博弈群组增益因子的分布将是大部分群组的增益因子都小于r0,而只有少数群组的增益因子大于r0.显然,如果没有少数具有较大增益因子的博弈群组的存在,占大多数的增益因子小于r0的群组中不可能有个体能够维持合作行为.

图5 参数取 g=5 与 r0=0.35 时博弈群组单元中合作者数目 wC 的分布Fig.5.Distribution of the numbers of cooperators in the group wC for g=5 and r0=0.35 .
为了更好地理解上述演化结果以及更全面地展示系统的演化过程,图 6 给出了对应图 5 演化结果的群体合作水平fC和群组中不同合作者数目wC对应的博弈群组比例f(wC) 的演化时间序列.如图 6(a)和图 6(b)所示,系统演化的暂态时间非常短,wC=3,4,5,对应的初始合作者数目较多的博弈群组比例随着系统演化开始后迅速下降为 0,即使初始时该部分群组中合作者策略是多数策略,但群组中的个体依然不能维持自身的合作行为.该部分群组中合作者数目逐步减少,使得wC=1,2 的群组比例在演化初始阶段有所上升,但此后依旧逐步减小到 0,群体的合作水平最终减小为 0 .在异质性较强的指数分布情况下,如图 6(c)所示,系统演化的暂态时间有所增长,虽然f(wC=3),f(wC=4)和f(wC=5) 随着演化的开始依旧比较快地下降,但最终依然能够存在一定比例的wC=1,wC=2,wC=3 甚至wC=4 的博弈群组,稳态时系统能够维持一定的合作水平.在图 6(d)对应的异质性最强的幂律分布情况下,系统的演化过程出现了本质的改变,系统暂态时间大大增长.wC=3,4,5 对应的初始合作者占多数的博弈群组比例随着系统演化的进行先缓慢减小到一个最低值后逐步上升到一定水平,增益因子的异质性对群体合作行为的涌现、维持和传播起到了重要的促进作用.在幂律分布情况下,具有较小增益因子的博弈群组,即使同样存在初始合作策略占多数的群组中的个体逐步转变为背叛者,由于存在少数具有非常高增益因子的群组,该部分群组中个体多数采取合作策略,形成了稳定的合作团簇.形成稳定合作团簇的群组能够将合作策略向周围群组中的个体传播,更多群组逐步被合作者占据,使得群体中合作个体比例在减小到一定值后能够最终逐步升高到一个较高的合作水平.
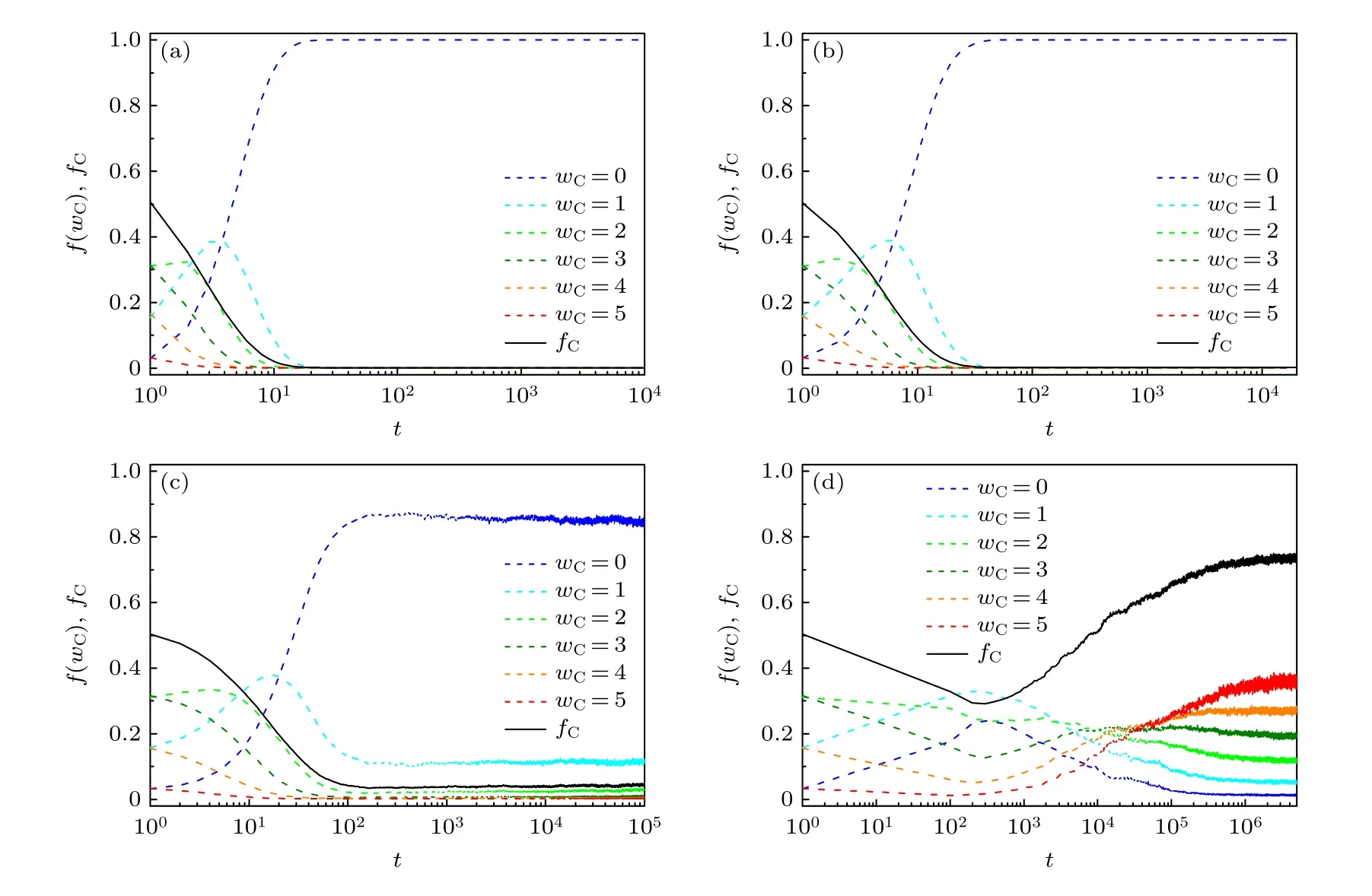
图6 4 种增益因子分布情况下,参数取 g=5 与 r0=0.35 时群体合作水平 fC 以及群组中合作者数目 wC 分别为0,1,2,3,4,5 的博弈群组比例的演化时间序列 (a) 原始模型;(b) 均匀分布;(c) 指数分布;(d) 幂律分布Fig.6.Time series for the evolution of the fraction of cooperators fC and the fractions of groups with wC=0,1,2,3,4,5 forg=5 and r0=0.35 :(a) Original model;(b) uniform distribution;(c) exponential distribution;(d) power-law distribution.
最后,研究4 种不同增益因子分布情况下,均匀超图上超边数目对临界增益因子均值rc的影响.图 7 给出了不同阶数g的超图上公共品博弈中rc随超图超边数目与超图全连通对应超边阈值的比值L/Lc的变化情况.从图 7 可以看到,在给定增益因子分布和超边数目比值L/Lc下,rc都会随着g的增大而减小.同时,在给定增益因子分布下,对于每一个超图阶数g值,rc随L/Lc的增大而增大.特别是在如图 7(a) 所示的原始模型的演化结果中,rc随L/Lc的增大而逐步增大到接近于 1,其他3 种特殊分布情况下同样有此趋势.rc=1 对应着均匀混合群体公共品博弈中合作涌现的临界增益因子[37].随着超边数目L的增大,超图将更加趋向于全连接超图,rc将更接近于 1 .此外,对比相同超边数目L和阶数g对应的4 种增益因子分布的演化结果,可以发现,rc值随着增益因子分布异质性的增强而减小,异质增益因子能够极大地促进超图上公共品博弈中合作行为的涌现.
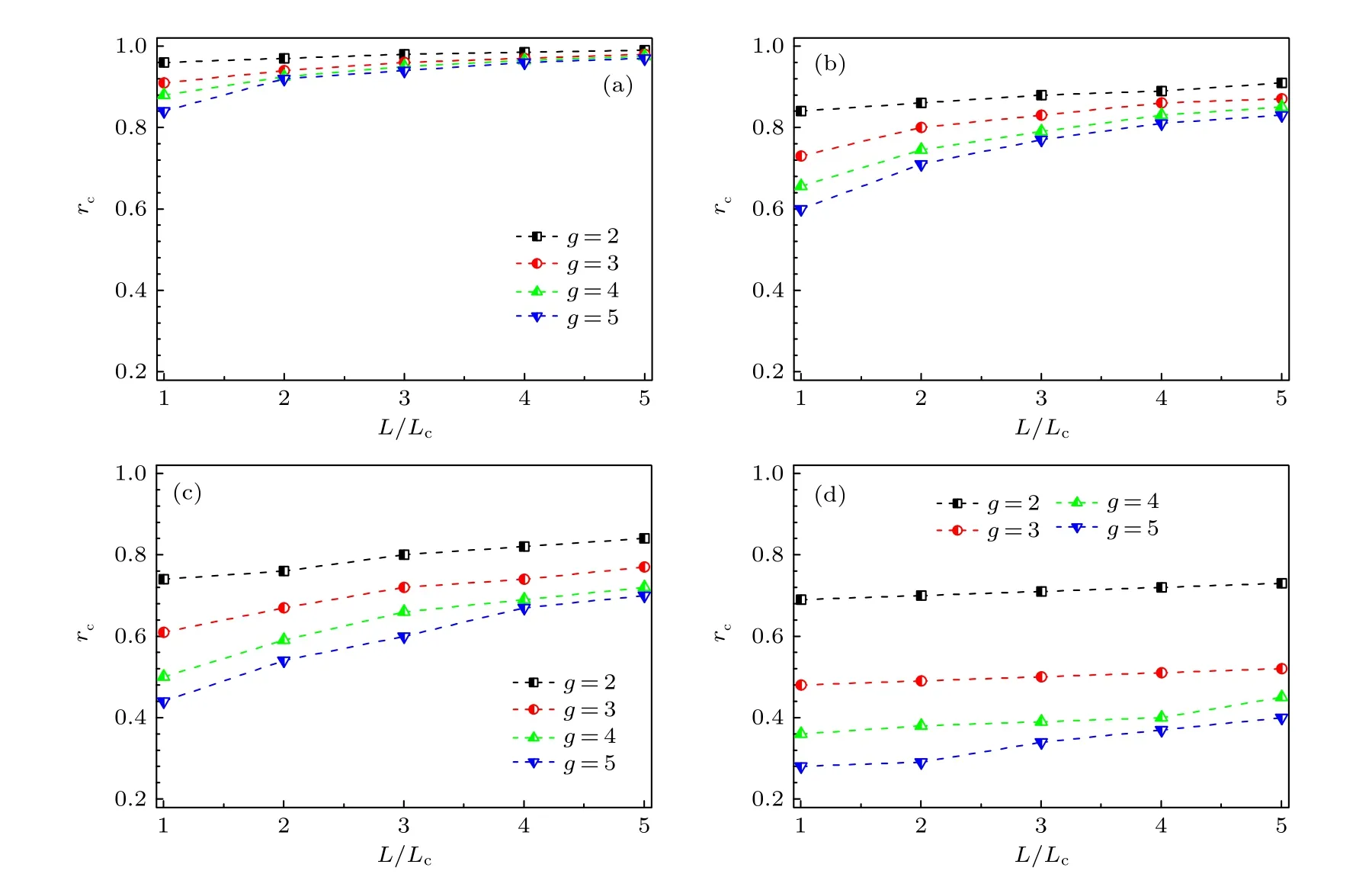
图7 4 种增益因子分布情况下,不同阶数 g 的超图上临界增益因子均值 rc 随超边数目 L 与阈值 Lc 的比值的变化 (a) 原始模型;(b) 均匀分布;(c) 指数分布;(d) 幂律分布Fig.7.Critical value of the synergy factor rc as a function of the ratio between the number of hyperlinks L and the critical value Lcin hypergraphs of different orders g :(a) Original model;(b) uniform distribution;(c) exponential distribution;(d) power-law distribution.
4 结论
本文考虑了公共品博弈中博弈群组增益因子的异质性,建立了基于均匀超图的具有不同增益因子分布的空间公共品博弈模型.除所有博弈群组具有相同增益因子的原始模型外,考虑了博弈群组增益因子具有相同均值并且分别服从均匀分布、指数分布和幂律分布的空间公共品博弈模型,研究了超图阶数以及增益因子异质性对于系统合作演化的影响.数值模拟结果表明,基于超边数目为L=Lc=(N/g)lnN的超图,无论是在博弈群组具有相同增益因子的原始模型中,还是在博弈群组增益因子服从异质性分布的空间公共品博弈中,对应群体中合作行为占主导的临界增益因子均值rc随超图阶数g的增大而减小,超图阶数的增大有利于提高系统的合作水平.同时,对比原始模型,群体中博弈群组增益因子异质性的引入能够显著促进群体中的合作行为.博弈群组增益因子的异质性对群体中合作行为的涌现和维持以及合作策略在群体中的传播起到了重要的促进作用.此外,基于上述模型,探究了超图超边数目对群体中合作演化的影响,发现临界增益因子均值rc随着超边数目L的增大而增大.并且,在不同的有限超边数目L值下,超图阶数g和增益因子异质性对于群体合作行为的促进作用同样存在.本文对考虑增益因子异质性的超图上空间公共品博弈中合作演化的研究,加深了对超图上空间公共品博弈中合作涌现的理解.
