定向红外光空间分布误差对冷冻靶温度场的影响分析*

郭富城 李翠 厉彦忠

(西安交通大学能源与动力工程学院,西安 710049)

1 引言

能源问题是当今社会人类文明发展遇到的颇具挑战性的战略问题[1-4].为了实现碳达峰、碳中和的战略目标,亟需一种洁净、高效、环保的能源形式[5,6].近年来,惯性约束核聚变(inertial confinement fusion,ICF)愈发受到世界许多国家的重视,其特点在于储量丰富、成本低廉、环境友好,因此极具发展潜力[7,8].随着高能激光的发展,小型可控的高能量密度热核聚变在实验室条件下已经可以进行.1972 年,Nuckolls 等[9]首先提出通过高能激光来引爆微小燃料靶丸从而实现热核聚变,球形靶丸内的燃料被烧蚀层引爆后的等离子体通过惯性约束在极小的空间尺度内,达到数亿摄氏度的高温,从而发生聚变反应.然而,热核聚变发生的条件极为苛刻,通常要求靶丸内燃料冰层厚度均匀性大于99%,燃料冰层内表面均方根粗糙度小于1 µm[10-15].燃料冰层的均匀性很大程度上由靶丸周围的温度场所决定,相对均匀的靶丸表面温度反应了相对均匀的靶丸内燃料冰层,因此冷冻靶温度场控制的重要性尤为突出[16,17].

ICF 冷冻靶靶丸内的燃料选择有两种:氘氘(DD)和氘氚(DT)[18].DT 作为热核燃料时,由于氚具有放射性,固态DT 冰层会由于氚的β衰变放热而发生自均化现象,即燃料冰层较厚的区域因为β 衰变热量更多而发生升华,并且在燃料冰层较薄的区域凝华,从而使得靶丸内的燃料冰层均匀性得到改善[19,20].由于氘不具有放射性,当DD 作为热核燃料时,无法产生类似于DT 的自均化过程,因此成冰质量较差.为了使DD 燃料冰层质量满足热核聚变的需求,需要通过外界辅助手段对靶丸温度场进行调控.现阶段的温度调控手段主要有控制铝套筒外的加热带功率,进而提升靶丸赤道区域的温度,提高温度均匀性,以及向柱腔内投射定向红外光,对靶丸表面的低温区域实现局部加热,从而提高靶丸表面温度均匀性.本文主要研究增设定向红外的形式对靶丸温度场的影响.

目前定向红外辅助均化的研究成果主要集中在美国劳伦斯利弗莫尔国家实验室.Kozioziemski等[21]通过TracePro 软件对红外光路进行仿真,计算出靶丸不同位置对红外的吸收功率,再将靶丸对红外的吸收功率作为源项输入至COSMOS 软件对低温靶温度场进行模拟,该方式计算可靠性很大程度上依赖于不同软件之间传递的数据精度,且模拟流程十分繁琐,但Kozioziemski 等提供了一个较为良好的定向红外辅助均化的研究思路,为后人的工作奠定了基础.London 等[22]在Kozioziemski的工作基础上研究了二维低温靶模型单侧及双侧红外注入形式下靶丸表面温度场的分布规律,但定向红外在腔内的传播具有很强的三维效应,因此二维计算结果与实际情况之间存在较大差距.Cook 等[23]研究了多种ICF 靶丸材料的红外吸收特性,并测量了等离子体聚合物和聚酰亚胺在正常氢化和完全氚化时的消光系数,为未来的定向红外辅助均化ICF 实验做准备.

在之前已发表的成果中[24],重点研究了定向红外布置形式为光纤插入式时靶丸表面温度特性,并且指出当光纤数量为6 时,靶丸表面温度均匀性达到最佳.本文的研究重点为定向红外布置形式为环形注入式时,由于红外光空间分布误差而导致的靶丸表面温度特性的变化规律,以期为未来的定向红外辅助均化实验提供技术性指导.

2 物理模型与数值方法

2.1 物理模型

冷冻靶结构尺寸参考美国NIF Rev5 靶型[25],具体的结构尺寸如图1 所示.该模型为柱腔结构,铝制热机结构(thermo-mechanical package,TMP)的上下两端冷环与硅冷臂连接,硅冷臂与低温制冷机相连,为冷冻靶提供冷量.热机结构内部为柱腔,内部高度10.01 mm,内径5.44 mm,上下两个半腔之间的间隙为0.02 mm.柱腔内表面镀金,金层厚度为0.02 mm.柱腔南北两端由封口膜密封,防止柱腔内填充的氦气泄漏.柱腔的中心位置为靶丸,如图1(b)所示,靶丸具有3 层结构,最外层为烧蚀层,受高能激光或X 光辐照后产生内爆压缩,中间层为氘燃料冰层,最内层为氘燃料气体层.整个冷冻靶系统置于一个较大的低温屏蔽罩内,用来屏蔽常温环境辐射.由于本文重点研究定向红外光空间分布误差对靶丸温度特性的影响,充气管及加持膜等部件不纳入研究范畴.

本文研究的定向红外配置方案为环形注入,如图2(a)所示,中空的锥形红外光透过南北两极的封口膜进入腔内,在柱腔的内表面上形成南北两个环形光带,定向红外经过柱腔内表面的反射后投射在靶丸表面上,从而实现对靶丸表面的局部加热.在图2(b)中,定义环形光带的宽度为d,南北光带的间距为ΔH.

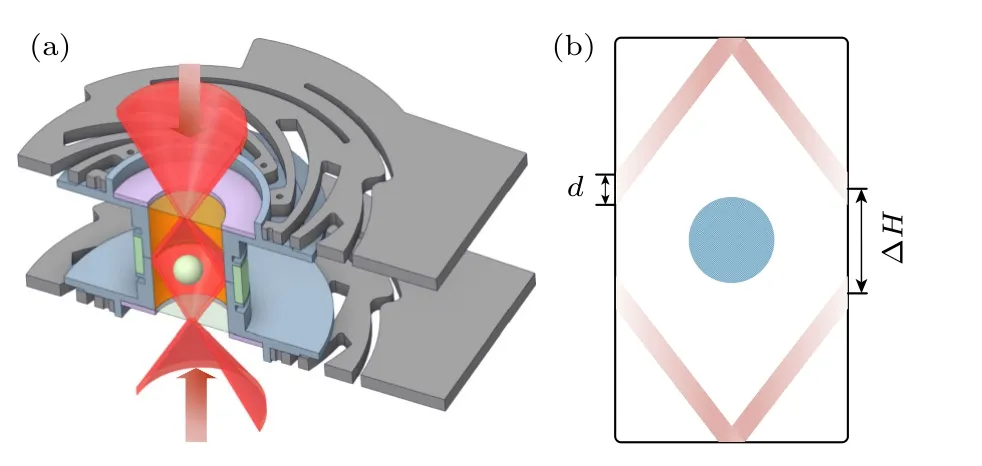
图2 环形注入定向红外示意图Fig.2.Schematic of directional infrared.

2.2 数值方法

为了研究定向红外条件下靶丸表面温度特性,需要将定向红外光路计算与温度场计算进行耦合.研究思路为通过蒙特卡罗方法对定向红外进行光迹追踪,并将红外辐照的结果转化为热贡献代入到温度场控制方程中进行计算,从而实现光-热耦合求解.具体控制方程如下.

1)根据相应的热物理边界来确定,确定光源粒子的初始位置及能量等相关参数.

2)确定光源粒子的下一个碰撞距离l及光源粒子的新位置.

光源粒子在一次传播过程中的碰撞距离l为

式中:r1为[0,1]区间内均匀分布的随机数,µa和µs分别为氦气的吸收系数和散射系数;对于无吸收和散射的理想气体而言,光源粒子沿原方向矢量持续传播.

3)判断光源粒子是否通过北极激光入射口和南极激光入射口逸出计算域,若是,停止光源粒子追踪;若否,继续进行下一步.

4)判断光源粒子是否与壁面发生碰撞,若是,执行步骤5);若否,执行步骤6);

5)根据壁面发射率判断光源粒子是否被壁面吸收,若是,计入热贡献,停止光源粒子追踪;若否,根据壁面漫射系数确定粒子反射方向.

光源粒子的新位置坐标为:

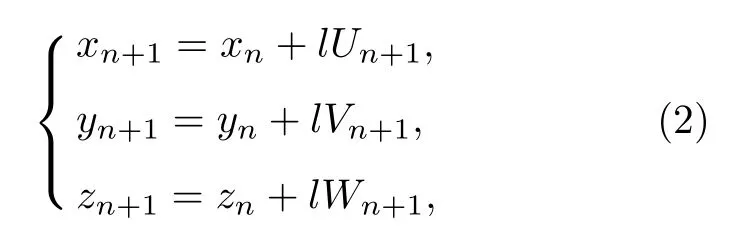
式中:x,y,z表示光源粒子在笛卡尔坐标系下的坐标值;下标n表示上一个状态,下标n+1 表示新状态;U,V,W表示粒子前进方向.

光源粒子接触到壁面后,一部分会被壁面所吸收,取[0,1]区间上的均匀分布随机数r4,记壁面吸收率为ε,若r4≤ε,则光源粒子被壁面吸收,每个被吸收的光源粒子对壁面热量的贡献为q;剩余的光源粒子会在壁面处发生反射,反射分为镜面反射和漫反射,记壁面的漫反射系数为df,取[0,1]区间上的均匀分布随机数r5,若r5≤df,光源粒子发生漫反射,反之发生镜面反射.

对于漫反射而言,分别取2 个[0,1]区间内均匀分布的随机数r6,r7,记壁面的单位法向向量a=(xn,yn,zn),随机向量b=(sin(2πr6)sin(2πr7),sin(2πr6)cos(2πr7),cos(2πr6)),若

则有

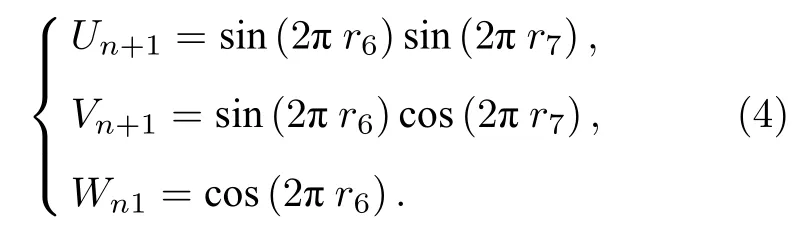
反之重新取一组r6,r7直至满足上述条件.

对于镜面反射,有

对于灰体模型,壁面发射率等同于壁面吸收率,壁面漫射系数反映了光源粒子与壁面碰撞后发生漫反射的份额占比.

6)根据单次反照度判断光源粒子是否被氦气中的杂质吸收,若是,计入热贡献,停止光源粒子追踪;若否,根据相位函数确定光源粒子的散射方向.

假定杂质粒子为球形粒子,发生碰撞后,光源粒子在垂直传输方向的平面内各个方向散射概率相同,因此在该平面内方位角φ的取值是任意的;光源粒子同杂质粒子碰撞后,碰撞后的速度矢量同碰撞前的速度矢量之间的夹角θ称为散射角,根据Henyey-Greenstein 相位函数计算求出,其中g为不对称因子,

光源粒子的前进方向为:

7)执行步骤2),直至光源粒子追踪停止.

8)将计入的光源粒子热贡献带入导热微分方程,并结合动量方程、连续性方程计算出冷冻靶温度场分布.

具体的计算流程如图3 所示.

图3 计算流程图Fig.3.Flow chart of calculation.

2.3 实验验证

2.3.1 定向红外数值模型验证

定向红外数值方法的实验验证通过北京卫星环境工程研究所完成的真空红外笼加热实验来进行[26].如图4 所示,在半径为55 cm 的金属伞面上安装了18 个宽度为7.7 cm 的天线筋(如图4 中蓝色区域所示),在金属伞面和天线筋上安装了6 个温度传感器(传感器位置如图所示)以收集温度数据.与金属伞面平行的半径为90 cm 的红外加热面位于其下方50 mm 处.整个实验装置被固定在1 个体积为510 m3的真空室中,以抑制其他形式的热传递.

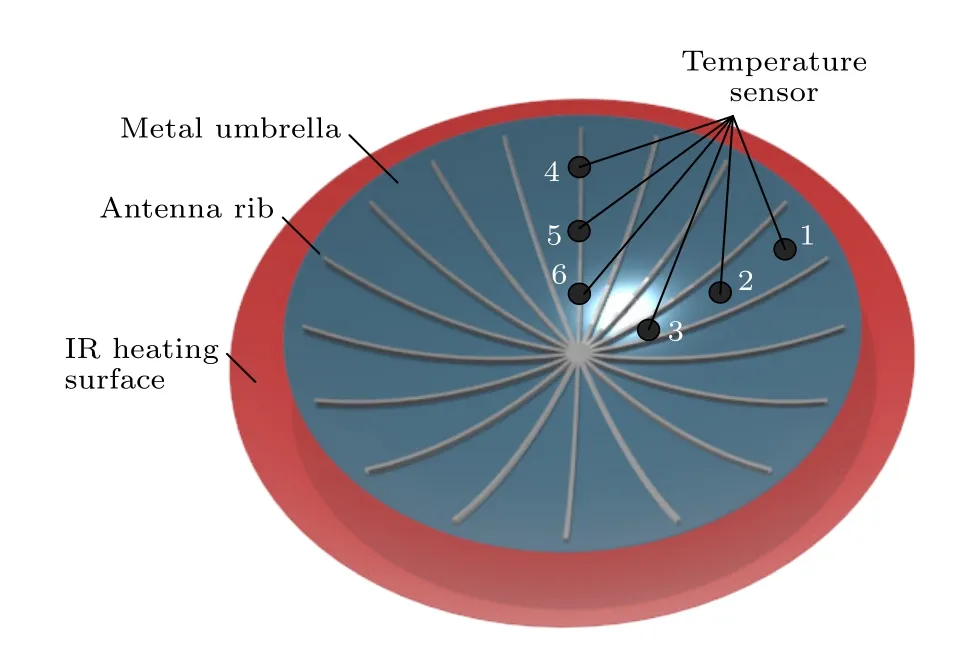
图4 真空红外笼加热实验装置示意图Fig.4.Sketch for an umbrella-shaped antenna and the IR heating surface.

实验条件如下:真空室内壁温保持在78 K,红外加热面功率为800 W,初始温度为环境温度.实验和模拟结果的比较如图5 所示.由于模拟和实验的初始条件不一致,在前50 min,实验和模拟的结果之间存在明显的差异.随着时间的推移,模拟结果能够很好地与实验结果相匹配,两者偏差小于5%,这表明所提出的红外模型具有良好的数值精度.

图5 实验结果与模拟结果对照Fig.5.Comparison of experimental and simulated results.

2.3.2 温度场计算模型验证

温度场计算模型的实验验证在之前的工作中已经完成,详情可参考文献[27].实验装置主要由2 个同心的柱状外壳组成:外部的壳体由黄铜制成,外径为33 mm,厚度为4.25 mm,高度为22.8 mm;中间的不锈钢壳体外径为21 mm,厚度为4 mm,高度为11.5 mm.2 个外壳分别代替冷冻靶装置中的柱腔和靶丸.在实验中,对冷环温度施加正弦扰动,正弦温度扰动的平均温度为28 K,振幅为0.5 K,频率从0.0009 Hz 到0.02 Hz 不等,氦气的压力保持在20 kPa.结果表明,实验测量和数值计算的温度波动振幅和频率基本吻合,在所有的研究工况下,两者相对误差均小于10%.因此,温度场计算模型能够对冷冻靶的温度分布进行相对准确的预测.

3 结果讨论与分析

本文主要研究了定向红外光空间分布误差对靶丸表面温度均匀性的影响规律,分析了几种不同的定向红外光空间分布误差形式对靶丸温度场影响的剧烈程度,进而为未来的定向红外实验进行理论指导.

3.1 无定向红外工况

无红外典型工况的边界条件如下:

1) 柱腔外低温屏蔽罩的温度为120 K,屏蔽罩发射率设为1.0;

2) 铝套筒上下冷环温度为18 K,铝套筒外表面发射率为0.05;

3) 铝套管南北两极封口膜透射率为0.05;

4) 金腔内表面发射率为0.03,且金腔内表面认为是朗伯散射体,即漫反射系数为1.0;

5) 腔内暂未设置红外光纤.

数值模拟中使用的材料物性见表1.

表1 不同材料在18 K 环境下的物性参数Table 1.Physical properties of different materials at 18 K.

靶丸外表面温度云图如图6 所示,受柱腔几何形状的影响,靶丸赤道区域距离柱腔内表面最近,因此传热强度最高,温度最低.靶丸南北两极会直接受到热机结构两端封口膜透射进来的环境辐射的影响,相较于靶丸其他区域温度偏高.

图6 靶丸外表面温度云图Fig.6.The temperature contour of the capsule.

为定量表征靶丸外表面温度均匀性,引入最大温差和加权温差两种计量方式,表达式为:

其中

式中:ΔTmax,ΔTw分别表示最大温差和加权温差;Tmax,Tmin分别表示温度最高值和温度最低值;Ti,Ai分别表示每个网格区域的温度值和网格面积;i,n分别表示网格索引和网格总个数;T¯ 为平均温度.通过(8)式,(9)式可以计算得出无红外工况下靶丸外表面最大温差为ΔTmax=0.843 mK,加权温差为ΔTw=0.221 mK.

3.2 定向红外理想注入工况

通过图6 可以看出,为了降低靶丸表面温差,提高温度均匀性,需要针对靶丸赤道区域进行局部加热,提升靶丸赤道区域的温度.靶丸赤道的温度区间约18.0077—18.0078 K,该温度区间的纬度跨度约占靶丸纬度总跨度的1/3,为了抬升靶丸赤道区域温度,决定采用d=0.3 mm (约靶丸直径的1/3),ΔH=0 的定向红外配置参数,即南北两侧的光带均投射在柱腔内表面赤道处,且光带的宽度为0.3 mm.图7 展示了不同光带功率密度q下靶丸表面温度云图,可以看出,随着光带功率密度的增大,靶丸赤道区域的温度被逐渐抬升,当q=1.4 W·m—2时,靶丸赤道区域的温度已经反超南北两极,成为靶丸表面温度最高的区域,因此一定存在合适的光带热流密度,使得靶丸表面的温度场相对均匀.

图7 不同光带功率密度q 下靶丸表面温度云图 (a) q=0 W·m—2;(b) q=0.8 W·m—2;(c) q=1.1 W·m—2;(d) q=1.4 W·m—2Fig.7.The temperature contours of the capsule under different q:(a) q=0 W·m—2;(b) q=0.8 W·m—2;(c) q=1.1 W·m—2;(d) q=1.4 W·m—2.

为研究使得靶丸表面温度均匀性达到极优值对应的光带功率密度,通过二分法进行了多光带功率密度工况研究,不同光带功率密度下靶丸表面温度特性如图8 所示,当q=1.2 W·m—2时ΔTw达到极小值0.03 mK,当q=1.25 W·m—2时ΔTmax达到极小值0.12 mK,两种温差评价标准的极优值对应的光带功率密度几乎一样,因此在后文中选择将q=1.25 W·m—2作为基准光带功率密度(折合单光带的功率为6.41 µW)进行研究.

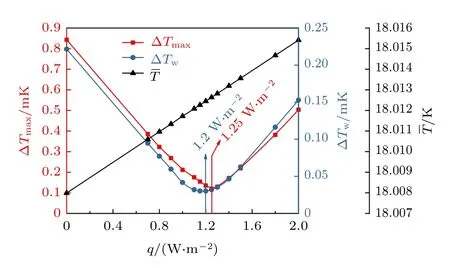
图8 不同光带功率密度下靶丸表面温度特性Fig.8.The temperature characteristics of the capsule under a series of q.

3.3 定向红外空间分布误差导致的光带宽度的变化

反射镜、聚光镜等精密光学器件的细微的装配误差会导致定向红外空间分布发生较大的偏差,常常会导致光带的宽度、光带的间距和光带的水平度等参数偏移预期设计,进而使得靶丸表面温度均匀性无法达到预设条件.本节主要研究定向红外空间分布误差导致光带宽度发生变化时,靶丸表面温度特性的响应情况.

分别研究了光带宽度d=0.20,0.25,0.30,0.35和0.40 mm,光带间距ΔH保持为0 的工况下,靶丸表面温度特性.单侧光带的总功率保持6.41 µW,南北两侧光带宽度同步变化.不同光带宽度下的靶丸表面温度云图如图9 所示.可以看出,在光带的总功率不变的前提下,相较于d=0.30 mm,当光带变窄,更多的热量会汇聚在靶丸赤道区域,从而导致靶丸赤道区域成为温度最高的区域,靶丸表面温度均匀性急剧恶化;当光带变宽,光带功率密度降低,靶丸赤道区域受到的红外辐射热流降低,赤道区域温度也会逐渐降低,同样地,光带变宽会使得定向红外更多地辐照在靶丸南北两极,使得两极温度进一步抬升.

图9 不同光带宽度下靶丸表面温度云图 (a) d=0.20 mm;(b) d=0.25 mm;(c) d=0.30 mm;(d) d=0.35 mm;(e) d=0.40 mmFig.9.The temperature contours of the capsule under different d:(a) d=0.20 mm;(b) d=0.25 mm;(c) d=0.30 mm;(d) d=0.35 mm;(e) d=0.40 mm.

图10 定量展示了当光带宽度发生改变时,靶丸表面温度特性的变化.从最大温差角度看,光带宽度相对于0.3 mm 变宽或变窄,都会导致靶丸表面最大温差的增大,光带宽度相对于0.3 mm 每缩短0.1 mm,最大温差涨幅约0.021 mK,光带宽度相对于0.3 mm 每增宽0.1 mm,最大温差涨幅约0.026 mK,由此可见光带增宽而导致的最大温差的涨幅更加剧烈.

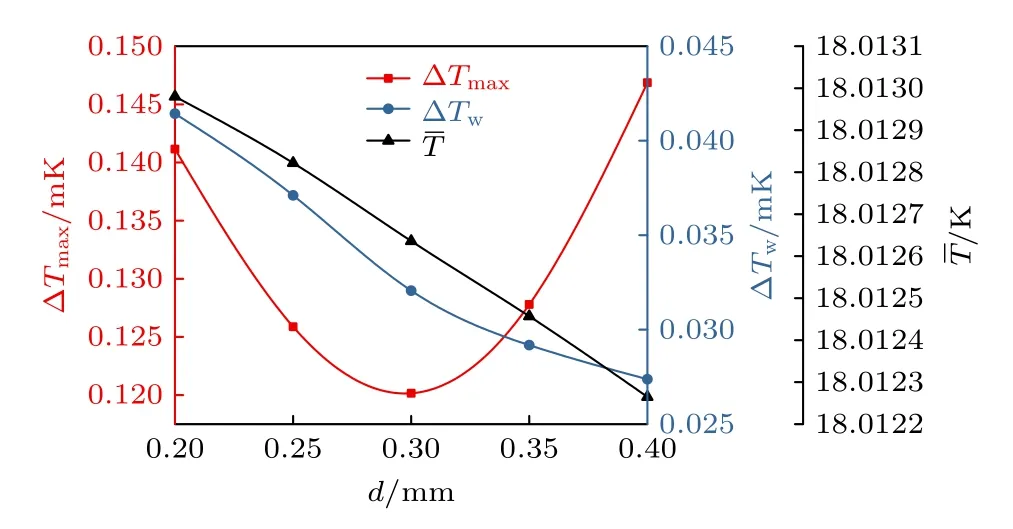
图10 不同光带宽度下靶丸表面温度特性变化曲线Fig.10.The temperature characteristics of the capsule under different d.

从加权温差角度看,在本文研究的范围内,加权温差随着光带宽度的增大而降低,根据图8 可知,当光带宽度为0.3 mm 时,加权温差最小值对应的功率密度为1.2 W·m—2,而本节设定的基准功率密度为1.25 W·m—2,略高于ΔTw对应的最优功率密度,因此当光带宽度增大时,光带功率密度会有所降低,加权温差会有所降低.相反,当光带宽度减小,红外的热量会更加集中地汇聚在靶丸赤道区域,导致靶丸赤道温度偏高,加权温差增大.

从平均温度角度看,靶丸表面平均温度随着光带宽度的增大而降低,在光带总功率保持恒定的前提下,光带宽度增大会使得靶丸表面的受红外辐照区域增大,辐照功率降低.靶丸表面更大的受辐照面积会使得靶丸吸收到的红外热量能够更快地向靶外传递,进而使得靶丸的平均温度降低.

综合来看,由定向红外空间分布误差导致的光带宽度的变化会使得靶丸表面温度均匀性恶化,且相比于光带宽度减小,光带宽度增大会使得靶丸表面温度均匀性恶化地更为剧烈.

3.4 定向红外空间分布误差导致的光带间距的变化

由定向红外空间分布误差而导致的光带间距的变化可以分为两种情况,如图11 所示.图11(a)表示单侧的光带位置偏离了柱腔赤道,另一侧的光带未发生偏移;图11(b)表示两侧的光带位置均偏离了柱腔赤道,且认为两侧光带偏离柱腔赤道的距离相同.下面分别就两种光带间距的变化形式进行讨论.

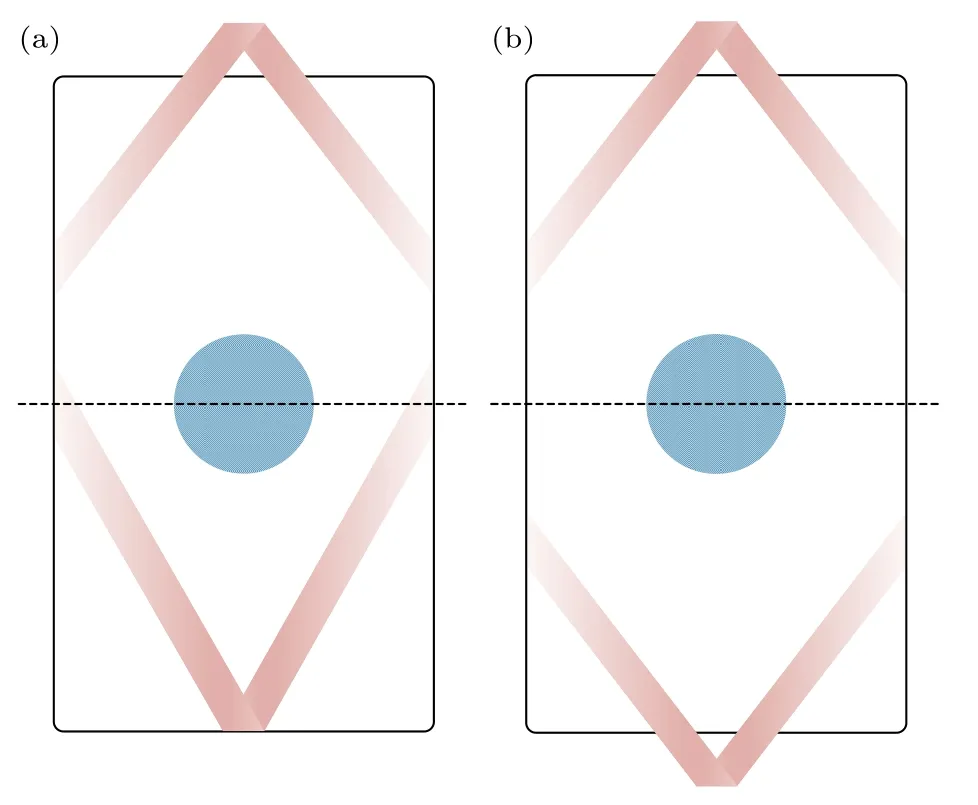
图11 光带间距变化示意图 (a)单侧光带偏移;(b)两侧光带偏移Fig.11.Schematic of the deviation of the IR bands:(a) Singleside IR band drifts;(b) both-sides IR bands drift.

3.4.1 单侧光带偏移

由于南侧光带位置向南偏移的计算结果与北侧光带向北偏移的结果基本相同,在此仅讨论北侧的光带位置向北偏移的情形.分别研究了北侧的光带位置向北偏移0,0.1,0.2,0.3,0.4,0.5 mm 时靶丸表面温度分布特性.单侧光带的总功率保持为6.41 µW,不同北侧光带偏移距离下的靶丸表面温度云图如图12 所示.从云图上可以看出,随着北侧光带逐渐向北偏移,靶丸的北半球温度有明显升高,靶丸南半球成为温度最低的区域,靶丸南北半球的温度差异逐渐显著.

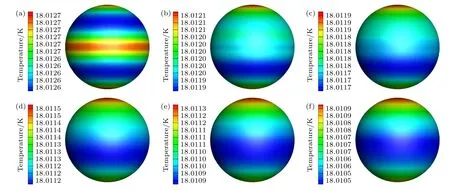
图12 不同北侧光带偏移距离下的靶丸表面温度云图 (a) 0 mm;(b) 0.1 mm;(c) 0.2 mm;(d) 0.3 mm;(e) 0.4 mm;(f) 0.5 mmFig.12.The temperature contours of the capsule at different offsets of the northern IR band:(a) 0 mm;(b) 0.1 mm;(c) 0.2 mm;(d) 0.3 mm;(e) 0.4 mm;(f) 0.5 mm.

图13 展示了不同北侧光带偏移距离下的靶丸表面温度特性变化曲线.随着北侧光带位置逐渐向北偏移,靶丸表面的最大温差和加权温差基本呈线性增大,增大的速率分别为0.709 K/m 和0.147 K/m,靶丸表面温度均匀性随之恶化;靶丸表面平均温度也随之降低,这是由于当北侧的光带向北偏移时,靶丸接受红外辐射的面积降低,使得靶丸吸收的红外热流减小,进而使得靶丸平均温度的降低.

3.4.2 两侧光带偏移

本文仅考虑南北两侧的光带向柱腔两极对称偏移的情形,非对称的偏移情况太过复杂,此处不做考虑.分别研究了两侧光带间距ΔH=0,0.2,0.4,0.6,0.8,1.0 mm 时靶丸表面温度特性.每侧光带的总功率保持为6.41 µW,不同光带间距工况下的靶丸表面温度云图如图14 所示.随着两侧光带间距的增大,靶丸赤道区域的温度逐渐降低.由于光带正对的位置逐渐靠近靶丸南北两极,导致靶丸南北两极与赤道区域的温差逐渐增大.

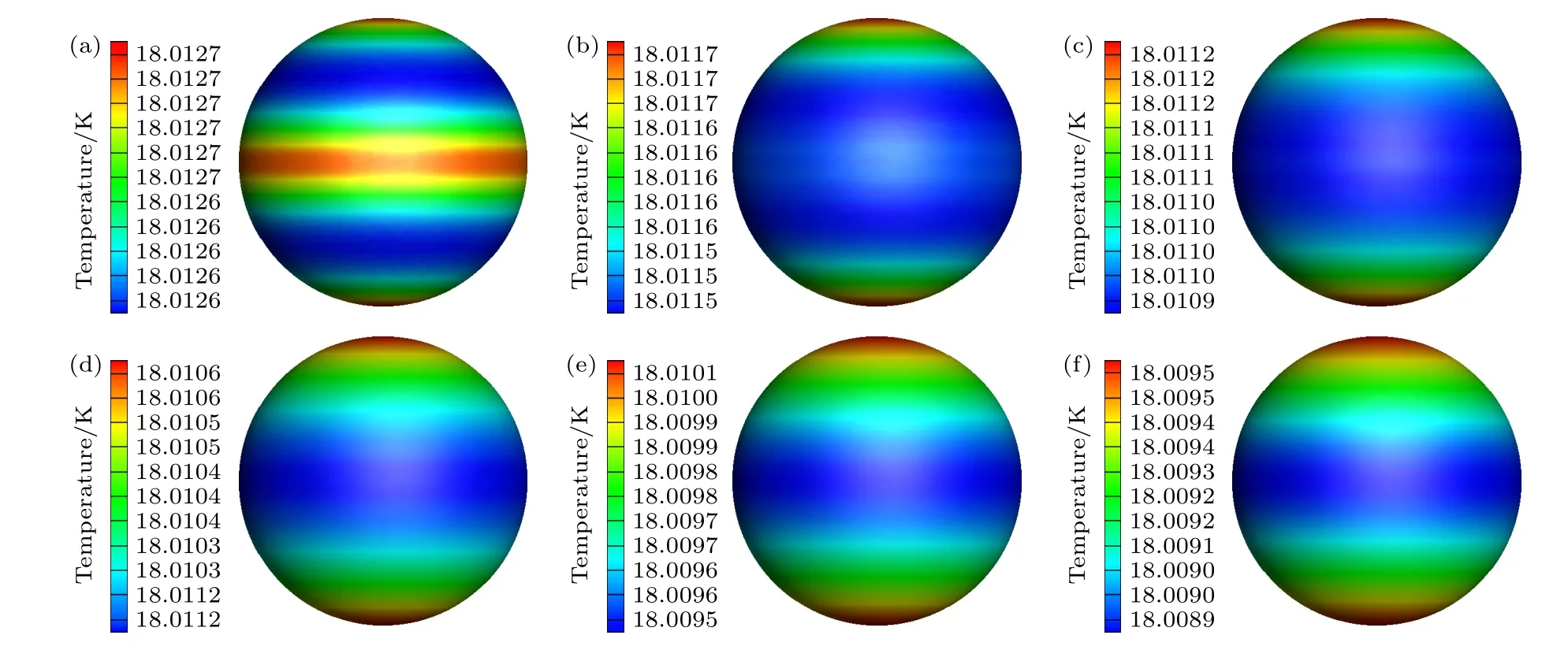
图14 不同光带间距下靶丸表面温度云图 (a) ΔH=0;(b) ΔH=0.2 mm;(c) ΔH=0.4 mm;(d) ΔH=0.6 mm;(e) ΔH=0.8 mm;(f) ΔH=1.0 mmFig.14.The temperature contours of the capsule under different ΔH:(a) ΔH=0;(b) ΔH=0.2 mm;(c) ΔH=0.4 mm;(d) ΔH=0.6 mm;(e) ΔH=0.8 mm;(f) ΔH=1.0 mm.

图15 定量地展示了不同光带间距下靶丸表面温度特性变化曲线.随着两侧光带间距的增大,靶丸表面最大温差、加权温差基本呈线性增大,增长速率分别为0.614 K/m 和0.141 K/m,靶丸表面平均温度随光带间距增大而线性降低,降低速率为3.489 K/m.

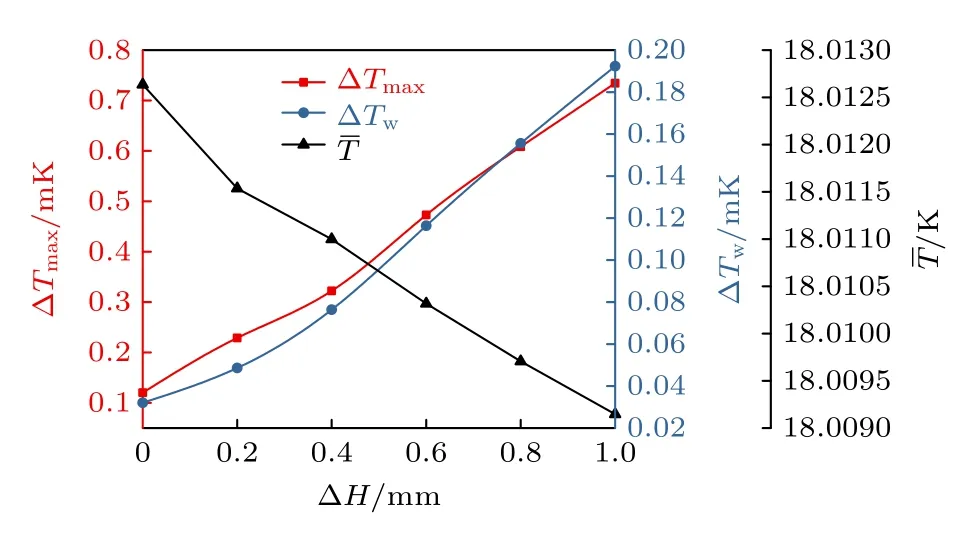
图15 不同光带间距下靶丸表面温度特性变化曲线Fig.15.The temperature characteristics of the capsule under different ΔH.

3.5 定向红外空间分布误差导致的光轴的偏心

由定向红外空间分布误差导致的环形红外光轴的偏心可以分为两种情况,如图16 所示.图16(a)表示南北两侧的环形红外光轴向同侧偏移,偏移的距离均为δ;图16(b)表示南北两侧的环形红外光轴向对侧对称偏移,偏移的距离为δ.下面分别就两种光轴偏移形式进行讨论.

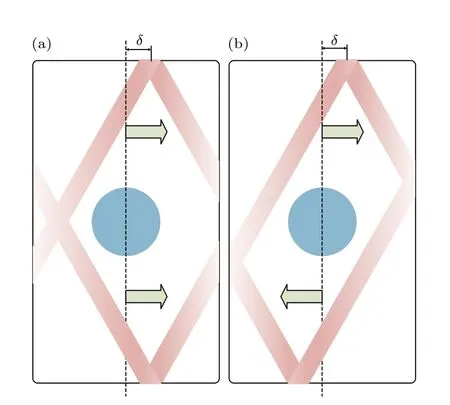
图16 光轴偏移示意图 (a) 光轴同向偏移;(b) 光轴对向偏移Fig.16.Schematic of IR bands axes offset:(a) The axes of the IR bands shift in the same direction;(b) the axes of the IR bands shift in the opposite direction.

3.5.1 南北两侧光轴同向偏移

研究了光轴偏移量δ=0,0.05,0.10,0.15,0.20,0.25 mm 等几种工况,每侧光带的总功率保持为6.41 µW.不同光带偏移量下靶丸表面温度云图如图17 所示.随着南北两侧光轴同向偏移距离的增大,靶丸表面赤道区域的温度均匀性发生明显的降低,但是靶丸的赤道区域仍然为最低温度所在区域,靶丸南北两极仍然为最高温度所在区域.图17(g)同时展示了δ=0.25 mm 时靶丸表面温度云图和柱腔赤道区域定向红外辐照热流云图,当南北两侧的光轴向同向偏移时,在柱腔内表面上会形成对称的倾斜光带,两光带的交汇点位于柱腔赤道区域,靶丸正对两光带交汇处的温度会有明显升高,从而造成了靶丸赤道周向温度的不均匀.

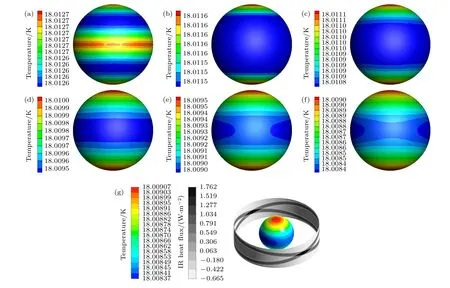
图17 不同南北两侧光轴同向偏移量下靶丸表面温度云图 (a) δ=0;(b) δ=0.05 mm;(c) δ=0.10 mm;(d) δ=0.15 mm;(e) δ=0.20 mm;(f) δ=0.25 mm;(g) δ=0.25 mm 靶丸表面温度云图和柱腔赤道区域定向红外辐照热流云图Fig.17.The temperature contours of the capsule under different δ:(a) δ=0;(b) δ=0.05 mm;(c) δ=0.10 mm;(d) δ=0.15 mm;(e) δ=0.20 mm;(f) δ=0.25 mm;(g) δ=0.25 mm,adding the radiation heat flux contour in the equatorial region of the hohlraum.

图18 展示了不同南北两侧光轴同向偏移量下靶丸表面温度特性变化曲线.随着两光轴偏移量的增大,靶丸表面最大温差和加权温差均有明显的增大,需要注意的是,靶丸表面最大温差和均匀性温差的变化在δ=0.10 mm 和0.15 mm 之间最为剧烈,这是由于光带倾斜的角度和光轴偏移量之间的函数关系并非线性的,而是呈三角函数关系,因此在两光轴偏移量变化的某区间内会发生靶丸温度均匀性剧烈变化的情形.靶丸表面的平均温度随两光轴偏移量的增大而降低,这是由于随着光带的偏移,定向红外辐照靶丸的区域从赤道逐渐向南北两极靠拢,造成有效辐射面积降低,从而导致靶丸平均温度的降低.为了方便对不同定向红外空间分布误差形式对靶丸温度场均匀性影响的敏感性分析,将靶丸温度特性的变化作线性近似,由此可得,靶丸表面最大温差和加权温差的增长速率分别为2.434 K/m 和0.586 K/m.

图18 不同南北两侧光轴同向偏移量下靶丸表面温度特性变化曲线Fig.18.The temperature characteristics of the capsule under different δ.

3.5.2 南北两侧光轴对向偏移

研究光轴偏移量δ=0,0.05,0.10,0.15,0.20,0.25 mm 等几种工况,每侧光带的总功率保持为6.41 µW.不同光带偏移量下靶丸表面温度云图如图19 所示.由于南北两侧光带对称地向对向偏移,两光带在偏移后正好重合,如图19(g)所示,倾斜的重合光带使得靶丸南北两极的高温区域位置发生偏移,南北两极高温区域的连线不再是沿着重力的方向.同时,倾斜的重合光带使得靶丸赤道区域的温度均匀性恶化,当光带辐照在柱腔赤道处时,靶丸赤道对应位置的区域温度较高,反之则处于低温状态.

图19 不同南北两侧光轴对向偏移量下靶丸表面温度云图 (a) δ=0;(b) δ=0.05 mm;(c) δ=0.10 mm;(d) δ=0.15 mm;(e) δ=0.20 mm;(f) δ=0.25 mm;(g) δ=0.25 mm,靶丸表面温度云图和柱腔赤道区域定向红外辐照热流云图Fig.19.The temperature contours of the capsule under different δ:(a) δ=0;(b) δ=0.05 mm;(c) δ=0.10 mm;(d) δ=0.15 mm;(e) δ=0.20 mm;(f) δ=0.25 mm;(g) δ=0.25 mm,adding the radiation heat flux contour in the equatorial region of the hohlraum.

图20 展示了不同南北两侧光轴对向偏移量下靶丸表面温度特性变化曲线.随着两光轴偏移量的增大,靶丸表面最大温差和加权温差均有明显的增大,靶丸平均温度则随之降低.靶丸温度特性变化的原因在前文已经叙述,此处不再赘述.靶丸表面最大温差和加权温差随着两光轴偏移量的增长速率为2.922 K/m 和0.673 K/m.

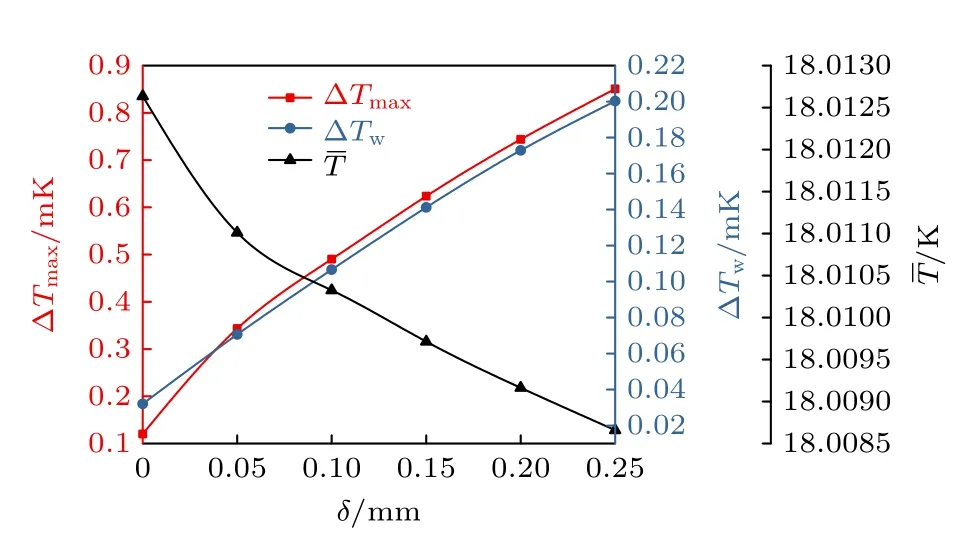
图20 不同南北两侧光轴对向偏移量下靶丸表面温度特性变化曲线Fig.20.The temperature characteristics of the capsule under different δ.

4 结论

本文研究了不同的定向红外空间分布误差下的靶丸表面温度特性变化规律,具体的误差形式有:光带宽度的变化,光带间距的变化(分别考虑单侧变化和双侧变化)及光带光轴的偏心(分别考虑同向偏心和对向偏心).图21 则对不同定向红外空间分布误差形式对靶丸温度场均匀性的影响进行归纳总结,整体而言,光轴偏心对靶丸温度场均匀性的影响最为剧烈,光带间距的变化次之,光带宽度的变化对靶丸温度场均匀性的影响最小.在实验中应当尽可能避免南北两侧光带的光轴的偏心,从而保证靶丸表面温度均匀性,进而可以保证靶丸内燃料冰层的均匀性.

图21 不同定向红外空间分布误差形式对靶丸温度场均匀性的影响Fig.21.Influence of different forms of directional IR spatial distribution errors on the temperature uniformity of the capsule.