Sun toughness and existence of P≥3-factor in two settings

LAN Meihui， GAO Wei

（1.School of Information Engineering，Qujing Normal University，Qujing 655011，China；2.School of Information Science and Technology，Yunnan Normal University，Kunming 650500，China）

Abstract： Motivated by toughness and isolated toughness，reference [9] introduced a new variable，sun toughness.For a non-complete graph G，its sun toughness s（G） is formulated by minimizing the ratio |S|/sun（G－S） with sun（G－S）≥2.In this paper，two statements have been obtained：（1）if a non-complete graph G satisfies κ（G）≥m and s（G）＞1 （resp.s′（G）＞3/2），G is a （P≥3，m）-factor deleted graph.（2）G is a （P≥3，k）-factor critical graph if s（G）＞（k+1）/3 or s′（G）＞（k+1）/2 when κ≥k+2（resp.s（G）＞（k+2）/3 or s′（G）＞（k+2）/2 when κ≥k+1）.Furthermore，we proved that these sun toughness bounds are sharp.

Key words： graph；path-factor；（P≥3，m）-factor deleted graph；sun toughness

1 Introduction

Graph modeling is applied to many computer problems.For instance，task allocation and scheduling problems can be analyzed by the graph coloring model；circuit board designing can be analyzed by several problems on the planar graphs；data packet splitting and transmission problems can be equivalent to the existence of factors in the graph.Specifically，due to the limitation of the transmission channel capacity，large blocks of data cannot be transmitted as a whole.Usually，large blocks of data need to be cut，distributed and transmitted，and then reassembled at the destination vertex.It equals to the existence of flow or fractional flow which can be measured by factors in corresponding network graph.Some related results on graph factors in various settings can refer to Gao et al[1－4]，Wu and Li[5]，Xu and Tao[6]，and Zhou et al[7－8].

Assuming G as a graph with vertex set V（G） and edge set E（G），we use dG（x） to denote the degree of any x∈V（G） in G.For any subset S of V（G） and E′ of E（G），we denote G-S and G-E′as the subgraphs by deleting the vertices of S and edges of E′ from G respectively.Denote ω（G） by the number of connected components of a graph G，and denote Pnby the path with n vertices where n≥2 is an integer.A path factor of a graph G is defined as a spanning subgraph whose components are paths.A P≥n-factor is a path factor such that every component contains at least n vertices.

Let k and m be non-negative integers.A graph G is called a （P≥n，k）-factor critical graph if any induced subgraph with order |V（G）|-k has a P≥n-factor.A graph G is called a（P≥n，m）-factor deleted graph if the resulting subgraph has a P≥n-factor，after deleting any m edges from G.Specially，when m=1，it is called a P≥n-factor deleted graph.If any induced subgraph of R with order |V（R）|-1 has a perfect matching，then graph R is a factor-critical graph.A graph H is called a sun if H≌K1or H≌K2or H is the corona of a factor-critical graph R having at least 3 vertices.We call the last class of sun with order at least six as big sun.The sun component refers to the component of G if it is isomorphic to a sun，and denoted sun（G） by the number of sun components in G.

Using the pattern of toughness and isolated toughness，Zhou et al[9]introduced a new toughness parameter called sun toughness s（G） which is formulated as follows

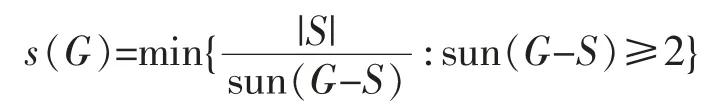
if G is not a complete graph.For complete graph G，s（G）=+∞.

Inspired by τ（G） and I′（G）（these parameters are the transformed version of toughness and isolated toughness），Zhu et al[10]introduced the variant of sun toughness denoted by s′（G） which is stated as follows

if G is not a complete graph；otherwise，s′（G）=+∞.

In order to prove the main results in next section，we need the following condition for a graph containin P≥3-factor from the view of sun component.

Lemma 1[11]A graph G has a P≥3-factor if and only if sun（G－S）≤2|S| for every S⊆V（G）.

Clearly，using the above lemma，we immediately get that G has a P≥3-factor if s（G）≥1/2.Intuitively，1/2 is the tight sun toughness bound for a graph admits P≥3-factor.However，Theorem 2 manifests the fact that 1/3 is the sharp bound instead of 1/2 when κ（G）≥k+2，and Theorem 3 reveals 2/3 is the tight bound when κ（G）≥k+1.

2 Main results and proofs

In Zhou's previous work[9]，they determined a sharp sun toughness bound for a 2-edge-connected graph having P≥3-factor after removing any edge e from graph.In this paper，we consider the general case of （P≥3，m）-factor deleted graph，while we use vertex connectivity condition instead of edge connectivity demand.

Theorem 1Let m∈N，and G be a non-complete graph with κ（G）≥m.If

then G is a （P≥3，m）-factor deleted graph.

Proof.By assumption of theorem，we infer δ（G）≥λ（G）≥κ（G）≥m and |V（G）|≥4.

For any E′⊆E（G） contains m edges，let G′=G-E′.We prove Theorem 1 in terms of acquiring that G′admits a P≥3-factor.In contrast，we assume that G′ has no P≥3-factor.In light of Lemma 1，there is a subset S⊆V（G′）=V（G） meeting

The whole proof can be divided into two cases in view of whether S is an empty set.

Case 1|S|≥1.

In this case，sun（G′－S）≥2|S|+1≥3 from （1），and we discuss two subcases according to whether S is a vertex cut set.

Case 1.1G-S is not a connected graph.

Following from connectivity assumption，we infer |S|≥m and ω（G－S）≥2.We treat the process of deletingedges in G-S as deleting edges one by one，and observe that deleting each edge in G-S may add at most two sun components.If sun（G′－S）≤sun（G－S）+m，then （since sun（G′－S）≥2|S|+1≥2m+1，we confirm sun（G－S）≥sun（G′－S）-m≥2m+1-m=m+1≥2）

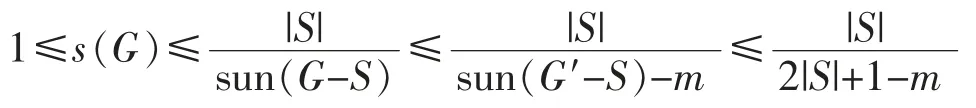
which leads to |S|≤m-1，a contradiction.

Now we consider sun（G－S）+m+1≤sun（G′－S）≤sun（G－S）+2m.Set t′=sun（G′－S）-sun（G－S）-m.Hence，t′∈{1，…，m} and there are at least t′ edges in E′ such that after deleting each edge，the number of sun component will add 2.Assume that there are exactly t edges in E′ such that after deleting each edge，the number of sun component will add 2，thus m≥t≥t′.Specifically，let T={e1，…，et} be the set of these t edges in G－S，and C1，…，Ctbe the components in G－S during the edge deleting procedure such that ei∈E（Ci） and the number of sun component add 2 after removing eifrom Ci（i∈{1，…，t}）.Note that K2■Ci（although delete edge in K2will process two sun components，K2is a sun component itself.Thus deleting edge in K2only add one sun component）.By observing，Cican be the following structures：

（1）P3or P4（a path with three or four vertices）；

（2）a big sun connects K1or K2with one edge；

（3）two big suns connected by an edge.We use the following way to get vertex set Di:（i∈{1，…，t}）；

（4）If Ciis isomorphic to P3or P4，then denote Diby a vertex in V（Ci） with degree 2 in Ci；

（5）If Ciis isomorphic to a big sun connects K1，then denote Diby the vertex set of factor-critical subgraph of big sun if K1is adjacent to a vertex in its factor-critical subgraph.Otherwise，K1adjacent to a vertex with degree 1 of big sun is denoted by u，and denote uw is an edge in big sun（see Figure 1）.The set Diis the vertex set of factor-critical of big sun except w，and then add vertex u into Di；

（6）If Ciis isomorphic to a big sun connects K2，then denote Diby the vertex set of factor-critical subgraph of big sun if K2connects a vertex with degree 3 in big sun by edge ei.Otherwise，K2connects to a vertex with degree 1 in big sun by an edge（see Figure 2），and the set Diis the vertex set of factor-critical subgraph of big sun except w，and then add vertex u into Di；

Figure 1 The second structure with a big sun connect K1

Figure 2 The second structure with a big sun connect K2

（7）If Ciis isomorphic to two big suns which is connected by an edge，then we consider the following three structures.（i）eiconnected two vertices with degree 1 in big suns.We mark one end of eias u，and uw is an edge in the big sun（see Figure 3）.In this case，denote Diby the vertex set of factor-critical subgraph of these two big suns except w and w′，and then add vertex u into Di.（ii） If the connecting structure as depicted in Figure 4，thendenote Diby the vertex set of factor-critical subgraph of these two big suns except w.（iii）As can be seen in Figure 5，the degree of vertices in edge which connects two big suns is 4 in Ci.We mark one of these two vertices as w，then denote Diby the vertex set of factor-critical subgraph of these two big suns except w.

Figure 3 The first structure of two big suns which are connected by edge ei

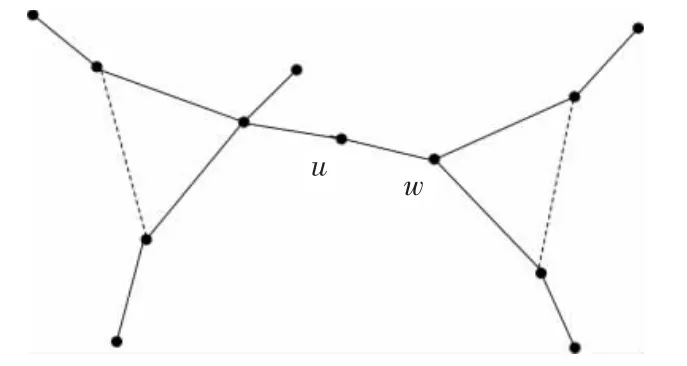
Figure 4 The second structure of two big suns which are connected by edge ei

Figure 5 The third structure of two big suns which are connected by edge ei

We verify |Di|=|V（Ci）|/2-1 or （|V（Ci）|-1）/2，and the number of sun components in Ci-Diis equal to |Di|+1.Since sun（G-S胰D）≤sun（G-S）+sun（C-D）（because the component Cimay not in G-S，and they produced by deleting some edges in E′），we need to discuss more components whose one edge is removed，the number of sun components add 1.

Let Xibe components in the process of deleting edges in G-S such that the number of sun components is increased by one after removing one edge from Xi，where i∈{1，…，sun（G′-S）-sun（G-S）-2t}.We select vertex subset Yiaccording to the structure of Xisuch that there are |Yi| isolated vertices will be processed in Xiafter deleting Yi.If Xi≌K2，then denote Yiby empty set.Otherwise，it implies that removing one edge from non-sun component Xi，it can be divided into a sun component and another non-sun component with at least three vertices.The structure of this non-sun component Xican be summarized into one of four structures in Figure 6.

Figure 6 The structures of four non-sun components

We consider the following circumstances.

（1）If Xiis isomorphic to structure described in Figure 6（a），then Yiis a vertex in non-sun component which connects K1or Yiis an empty set.This is because this non-sun component which connects K1in Ximay become one of Ciif we continue deleting some edges from it.Indeed，in this case，if K1connects exactly a vertex in Dior an isolated vertex in Ci-Di，then Yi=Ø；if K1connects to a vertex in K2in Ci-Di，then Yiis a vertex which connects K1in Xi（for instance，in Figure 4，uw is a K2component in Ci-Di，and if u is exactly a vertex connect K1，then Yi={u}）.

（2）If Xiis isomorphic to structure described in Figure 6（b），then Yiis a vertex in K2which connects nonsun component.

（3）If Xiis isomorphic to structure described in Figure 6（c），then Yiis the vertex set of factor-critical subgraph of big sun.

（4）If Xiis isomorphic to structure described in Figure 6（d），let u be a vertex with degree 1 in big sun which has another edge connecting to non-sun component，and w be a vertex in factor-critical subgraph of big sun which associates to u.Then Yiis the vertex set of factor-critical subgraph of big sun except w，and then add vertex u into Yi.

We state that if Yi=Ø in the special situation of Figure 6（a），we consider sun（Xi-Yi）=0.Set

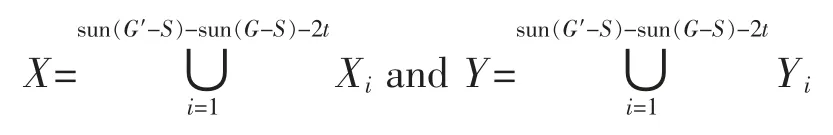
Combining the above discussions，we acquire（note that the value of |Y| can be taken zero，for example，when t=m or K2components in G-S are enough large and edges in E′ belonging to Xiare contained in these K2components）

since |S|≥m，a contradiction.

For s′（G），we have

a contradiction.

Case 1.2G-S is still a connected graph.

In this case，ω（G）=ω（G-S）=1，and after removing each edge from G-S，the number of its components adds at most 1.That is to say，sun（G′－S）≤ω（G′-S）=ω（G-S-E′）≤m+ω（G-S）=m+1.Therefore，combining with （1），we acquire 2|S|+1≤sun（G′－S）≤m+1，i.e.，|S|≤m/2.Furthermore，δ（G-S）≥λ（G-S）≥κ（G-S）≥κ（G）-|S|≥mm/2=m/2.

Since sun（G′－S）≥3，we ensure that at least：

（1）three vertices in G′－S have degree 0，or

（2）two vertices in G′－S have degree 0 and two vertices in G′－S has degree 1，or

（3）one vertices in G′－S has degree 0 and four vertices in G′－S has degree 1，or

（4）six vertices in G′－S has degree 1.

We consider the following subcases according to the value of m.

（5）If m=1 or 2，then δ（G-S）≥1 and the only possible to delete 2 edges in G-S and produce three sun components in G′－S.In this case，m=2，sun（G′－S）=3，|S|=1.Let SC1，SC2，SC3be three sun components in G′－S，where SC1and SC2is connected by e1，and SC2and SC3is connected by e2in G-S.If SC2≌K1，then we get

and

This leads a contradiction.

If SC2isomorphic to K2or a big sun，then we can select a vertex subset W in G-S in light of the tricks similar to discussed in Case 1.1 such that the number of sun components in G-S is exactly |W|+1 after removing W.Thus，we yield

and

a contradiction.

（6）If m=3，then δ（G-S）≥2.To produce at least three sun components in G′－S，we need delete at least four edges in G-S，a contradiction.

（7）If m≥4，then，to produce at least three sun components in G′－S，we need remove at least

edges from G-S，a contradiction.

Case 2If S is an empty set.

According to （1） we acquire sun（G′）>0.We have the following claim.

Claim 1If |S|=0，then sun（G′）=1.

Proof.Assume sun（G′）≥2.

If one of sun component of G′ is a big sun，then it is generated by deleting at least 3m-6 edges in G，we further have m=1.Hence，G isomorphic to a big sun connects to another sun by an edge.By means of discussion presented in Case 1.1，we can select S from V（G） such that G-S has |S|+1 sun components，which means

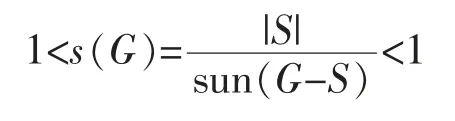
and

a contradiction.

If one of sun component of G′ is K2，then it is generated by deleting at least 2（m-1） edges in G，thus m=1 or 2.If m=1，then G≌P4.Thus s（P4）=1/2 and s′（P4）=1，a contradiction.If m=2，then G≌C4（an even cycle with 4 vertices）.We have s（C4）=1 and s′（C4）=2，which contradicts to s（G）>1 and s′（G）> 2 when m=2.

The last case is that all the sun components in G′ are isolated vertex.By δ（G）≥m and |E′|=m，G isomor-phic to K2which contradicts to the assumption that G is not complete.□

In terms of Claim 1，we confirm G′=G-E′ is a big sun.Therefore，there are at least three vertices has degree 1 in G′.If m≥2，then contradicts to E′ only has m edges and δ（G）≥m.Therefore，m=1 and G isomorphic to a big sun add one more edge.Let S be the factor-critical subgraph of the big sun，and then we get

and

a contradiction.

In all，we finish the proofing of Theorem 1.□

The following result reveals the relationship between sun toughness and （P≥3，k）-factor critical graphs.The tricks used to prove Theorem 2 follows from Gao et al[2]，and we skip the detailed proofing process here.

Theorem 2Let k∈N∪{0} and G be a graph satisfies κ（G）≥k+2.If s（G）>（k+1）/3 or s′（G）>（k+1）/2，then G is （P≥3，k）-factor critical.

If we revise κ（G）≥k+2 to κ（G）≥k+1，then when S≠Ø we can’t deduce sun（G-U）=sun（G′）=0 where U⊂V（G） with |U|=k，G′=G-U，and S⊆V（G′） with 2|S|+1＜sun（G′-S）.While we still get G-U is connected since κ（G）≥k+1.If G-U≌K2then G is a complete graph by means of δ（G）≥κ（G）≥k+1.If G-U is a big sun，then under the counterexample hypothesis，we have s（G）≤（k+2）/3 and s′（G）≤（k+2）/2.Therefore，we obtain the following conclusion.

Theorem 3Let k∈N∪{0} and G be a non-complete graph satisfies κ（G）≥k+1.If s（G）＞（k+2）/3 or s′（G）＞（k+2）/2，then G is （P≥3，k）-factor critical.

3 Sharpness

First，we show that the sun component conditions in Theorem 1 are sharp.Let m∈N，H1be a big sun and R1be its factor-critical subgraph.Hence，dH1（x）=1 for arbitrary x∈V（H1）V（R1） and |V（R1）|=|V（H1）|/2≥3.Choose v1∈V（H1）-V（R1） and u1≠V（H1）.Let H1′ be a graph with V（H1′）=V（H1）∪{u1} and E（H1′）=E（H1）∪{e1}with e1=u1v1.We get other m-1 copies of H1′，and denoted by H2′，…，Hm′，respectively.A graph G is constructed asWe select，where wi∈V（Ri） and viwi∈E（Ri）.be a subset of E（G） with m edges.Thus，we get

and

Therefore，for any positive integer m，we confirm

On the other hand，let S=V（Km）.Then we get sun（G－S-E′）=2m+1>2m=2|S|.According to Lemma 1，G-E′has no P≥3-factor，i.e.，G is not a （P≥3，m）-factor deleted graph.Hence，s（G）≥1 （or s′（G）>1） for m≥3 is tight.

Considering G=K1∨G1（see Figure 7） where G1is constructed as follows：SC1and SC2are suns，v is a vertexin G1which connects SC1and SC2by e1and e2，respectively.Set S=V（K1）∪{v}，then we obtain

and

Let G′=G-{e1，e2}.Then sun（G′-K1）=3>2=2|V（K1）|，thus G′ has no P≥3-factor and G is not a （P≥3，2）-factor deleted graph.Therefore，s（G）>1（or s′（G）>2） for m=2 is sharp.

Let H be a big sun with exactly six vertices，and G be a graph by adding an edge e in H as depicted in Figure 8.Let S be the vertex set of factor-critical subgraph of H，then s（G）=|S|/sun（G－S）=1 and s′（G）=|S|/（sun（G－S）-1）=3/2.On the other hand，delete e from G，then G-e its self a big sun which has no P≥3-factor（by setting S=Ø，then verifying using Lemma 1）.Thus，G is not a （P≥3，1）-factor deleted graph，and s（G）>1（or s′（G）>3/2） for m=1 is tight.

Figure 7 A counterexample of Theorem 1 when m=2

Figure 8 A counterexample of Theorem 1 when m=1

Considering G=Kk+1∨3K2，we have κ（G）=k+1，s（G）=（k+1）/3 and s′（G）=（k+1）/2.Let U be a vertex set in Kk+1with k vertices and G′=G-U=K1∨3K2.Set S=K1in G′，and we have sun（G′-S）=3>2=2|S|.That is to say，G′has no P≥3-factor and thus G is not （P≥3，k）-factor critical.Therefore，κ（G）≥k+2 and s（G）＞（k+1）/3 （resp.s′（G）＞（k+1）/2） in Theorem 2 can't replace to κ（G）≥k+1 and s（G）≥（k+1）/3 （resp.s′（G）≥（k+1）/2）.

To see Theorem 3 is sharp，let’s consider G=Kk∨G′ where G′ is a big sun with exactly six vertices（the factor-critical subgraph of G′ contain exactly three vertices）.Hence，we have κ（G）=k+1，s（G）=（k+2）/3 and s′（G）=（k+2）/2.Let U=V（Kk），G′=G-U，and S=Ø.Thus，sun（G′-S）=1>0 =2|S|，which implies G′ has no P≥3-factor and thus G is not （P≥3，k）-factor critical.

4 Conclusions and open problems

The main findings of this paper can be summarized as follows in which these results are against our intuition.

（1）Intuitively，under the condition κ（G）≥m，the tight sun toughness bound for a graph to be （P≥3，m）-factor deleted should be a function of m，i.e.，at the beginning we thought this bound should increase as m increases.However，Theorem 1 reveals that the sharp bound of sun toughness for （P≥3，m）-factor deleted graphs is a constant which is independent of the value of m.

（2）Lemma 1 seems to imply that 1/2 should be a tight bound for a graph admits P≥3-factor.Our second and third main results described in Theorem 2 and Theorem 3 present the best sun toughness bounds for （P≥3，k）-factor critical graphs in setting κ（G）≥k+2 and κ（G）≥k+1 respectively，where k is a non-negative integer.When k=0，we really found that the previous intuition is completely wrong，and s（G）＞1/3 for κ（G）≥k+2 （resp.s（G）＞2/3 for κ（G）≥k+1） is exactly the sharp bound for a graph permits P≥3-factor.

In Zhou et al[9]，they proved that a 2-edge-connected graph is P≥3-factor deleted if s（G）≥1.We note that in Zhou's work，they use edge connectivity condition，while in our paper we use the vertex connectivity conditioninstead.We raise the following conjecture on the edge-connected condition.

Conjecture 1Let m∈N，and G be a m+1-edge connected graph.If s（G）≥1（resp.s′（G）＞1），then G is a（P≥3，m）-factor deleted graph.

We found that after changing the vertex connectivity condition to edge connectivity condition，the problem will become much more difficult where the tricks presented in Theorem 1 can not be available any more.New technologies are needed to conquer the above conjecture.

As the end of our paper，we raise the following open problem for future on-going works.

Problem 1What are the tight bounds of s（G） and s′（G） for a graph G to be a （P≥3，m）-factor covered graph?