An Approach for Connector Arrangement of Very Large Floating Structures

-,-,-,,,-

(1.State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body,Hunan University,Changsha 410082,China;2.School of Hydraulic Engineering,Changsha University of Science&Technology,Changsha 410114,China;3.China Ship Scientific Research Center,Wuxi 214082,China)

Abstract:Connectors have a great impact on responses of multi-modular floating systems,but there is no rule to obey for how to reasonably arrange the connectors on the module’s end face. This paper presents a scientific strategy for determination of the best connector layout for very large floating struc⁃tures (VLFS). To do so, a network model of VLFS was established for analyzing the effect of connector layouts on the system responses. To identify the most influential factors for optimization, a sensitivity analysis was employed to evaluate the relationship between the location of connectors and dynamic re⁃sponses of modules and connectors. And an optimal strategy was proposed to determine the layout of connectors based on individual objectives according to specific engineering requirements and con⁃straints for various sea states.In numerical studies of a three-modular floating system,the optimal con⁃nector layout was found for different weight combinations. The work provides a tool for the layout de⁃sign of connectors according to practical needs in engineering.

Key words:very large floating structure;connector arrangement;sensitivity analysis;optimal connector layout

0 Introduction

Very large floating structures (VLFS) is the one of the most effective inventions to exploit the oceans,where there exist a vast area and abundant resources.The concept of VLFS was proposed in 1924 by Armstrong[1]who invented a sea station aimed to help people cross the Atlantic ocean. In the last forty years, the VLFSs have been studied in marine engineering for floating farms, floating industrial platforms, floating military platforms, and even floating cities[2]. Japan and the United States were leading the research on the VLFS earlier. The Phase 1 construction of Kansai Interna⁃tional Airport was proposed by Japanese in 1973. Although the proposed floating structures were not accepted, the studies in this field had already begun in Japan[3]. Then, the Technological Re⁃search Association of Mega-float (TRAM) was founded in 1995, which is a major milestone for the VLFS studies in Japan. Subsequently, this association carried out a lot of researches on the pon⁃toon-type VLFS[4-5], and the hydro-elastic problems related to VLFS had been intensively investi⁃gated[6]. Around this time, American navy proposed a Mobile Offshore Base (MOB) project. This floating structure was mainly used in the open sea and for the military purposes initially[7-8].Motivat⁃ed by commercial SeaBase designer needs, hydrodynamic studies had been conducted for the MOB[9]. Besides these two countries, other coastal countries have also exhibited strong interest in the studies of VLFS.The marine farming of salmonids began in Norway in the 1960s,and the largescaled floating fish cage as a kind of VLFS has also attracted much attention[10].With the level of the sea rising, the Dutch plan to live on the water. The floating houses, floating towns and even floating islands all are considered[11-12]. Furthermore, some floating entertainment facilities, such as hotels and restaurants,also have been constructed in Australia,North Korea and Hong Kong[13].

The VLFS is characterized by its massive size and complexity functions,thus it is necessary to analyze whether the VLFS satisfies stringent design and functional requirements[14]. The early re⁃searchers tended to treat VLFSs as continuum structures, but the single continuum structures with the kilometer scale may suffer large hogging moment.Meanwhile,the structures would induce many problems in manufacturing as well as transportation[15]. In this regard, some scholars tried to modu⁃larize the VLFSs by varied connection forms[16]. The connections were initially designed as rigid joints,but this kind of connections may induce large shear forces upon investigation[17].As known to all,the hinge-type connections is an effective way to release the pitch motion between the modules.However, the cost is the increase in modules’responses for heave and pitch motions[17-18]. Some scholars tried to balance the relationship between the responses of modules and the forces of con⁃nections, therefore a mechanical joint which could change the rotation stiffness was invented. As shown in the results, the responses of modules are greatly affected by the connectors’stiffness[19].Hence,the flexible connectors had received more concerns[20].Although flexible connectors can sig⁃nificantly reduce connection forces, the flexible connectors still inevitably encounter relatively large responses of modules in some wave frequencies or wave incident angles[21]. In 1999, Haney[22]did a review work about the MOB connectors. It seems that the compliant connectors involving the normal hinge and flexible parts are more applicable to the engineering practice. However, the nu⁃merical simulation of the compliant connector is more complicated and it will be more difficult to maintain.Apart from the studies of connection forms,there are many other researches related to the connection. Michailides et al[23]discussed the grid type of floating structures’layout with a flexible connection.The results indicate that there are some complex relationships between the connectors’stiffness and the optimal layout of floating structures.Zhang and Xu[24]compared several topological configurations of flexible connectors. The compound connection form can achieve a better AD sta⁃bility of the floating structure. Gao and his co-workers[25]studied on the location of the VLFS con⁃nection in longitudinal direction, the results show that the optimal location could achieve maximum reductions in the structures’responses.

Although many works have been done on connectors, the understanding of the connector lay⁃out on modules’end face is somehow fragmented. Many researchers may have a preliminary con⁃sensus that aligning connectors to the sides of the module is better for reducing the connection load,or the horizontal spacing of the connector is set the same as that of the module’s columns for better strength of modules[26–28]. However, two important issues should be carefully considered in the VLFS design. One is the response of modules, which is related to the stability and functionality of the VLFS. The other is the connector load, which is related to the strength designs of modules and connectors. It is commonly known that the arrangement of connectors has a significant impact on these two issues. However, the intrinsic influence of the connector layout has not been fully under⁃stood, because there are so many influential factors combined to finally affect the module response and connector load.The factors include the module structure,wave condition(wave height,frequen⁃cy, direction, etc.), engineering concerns (the requirement on the module stationery, strength con⁃straint, some special safety requirements), and connector layout (number of used connectors, loca⁃tions, stiffness, arrangement in different directions, etc.). A good design of the connector layout should comprehensively take these influential factors into consideration, which has not been done yet. The current situation is that understanding of connector layout is fragmented, intuitive, incom⁃plete, and even somehow biased, lacking a comprehensive cognition. This is why there has been no effective solution for the arrangement of connectors.Since this specific topic is very important to the performance of modularized VLFS, it is essential to develop an approach that can wisely determine the connector's layout according to engineering requirements.

In this paper,an inclusive approach was proposed to determine an appropriate configuration of flexible connectors for VLFS, based on the principle that the resultant modular responses and the connector forces should be retained as small as possible or within special requirements. Firstly, in order to analyze the effect of the connector layout, a mathematical model for the semi-submersible type of VLFS was built by using the network modeling method which allowed flexible alteration of the location and number of connectors. Then, a sensitivity analysis based on the orthogonal experi⁃ment method[29-30]was conducted to understand the relationship between the location of the connec⁃tor and the dynamic responses of the VLFS system, in order to find the most influential factors for later optimization.At last,an optimal assessment model was established for comprehensive analysis according to specific engineering requirements and constraints.In numerical studies,a three-modu⁃lar floating system was considered for the optimal connector layout for various scenarios of weight combinations.The superiority of the optimal connector layout was also discussed by comparing with two normal layouts.

1 Modeling of the VLFS

In order to study the effect of connector layout, a mathematical model was built by using the network modeling method[31]that treats modules as oscillators and connectors as couplings. This modeling method allows us to flexibly rebuild the floating system model by adjusting oscillators and couplings.

Two coordinate system are used in this modeling. As shown in Fig.1,Oxyzis defined as the global coordinate system.Oiηiζi ξiis the local coordinate system ofi-th module and its originOiis placed at the gravity center of the module. Thez-axis andξi-axis are pointing upwards. Further⁃more, thex-yplan andηi-ζiplan coincide with the undisturbed free water surface.

1.1 Equations of motion

Thus the forces and responses of the modularized VLFS can be conveniently de⁃rived in the frequency domain[32], the equation of motion is formulated directly as follow:

Fig.1 Sketch of coordinate systems

wherekx,ky,kzare the translational stiffness of the connector,respectively.

The stiffness of the connector is an important influential factor which has been intensively studied in the report[33].In this paper,the stiffness is set at 1010N/m for each direction which results in a better stationery state of the floating platform. In this regard, the stiffness of connector will not be treated as a design variable for later analysis.

Reviewing the equations before, Eq.(1) is not sufficient to obtain all the displacements includ⁃ing modules and hinges.The force balance equations should be added as follow:

in whichFkmandFnmrepresent the forces of Connectormthat acting atk-th module andn-th mod⁃ule,respectively.

1.2 Irregular-sea response

In this paper,the floating structure is considered to be deployed in irregular sea.The 2-param⁃eter Bretschneider wave spectrum is applied[27].The input wave spectrum,S(ω),can be written as:

1.3 Parameters of the floating structure

The VLFS simulated in this paper is a three-modular platform connected along the longitudinal direction. The perspective view and the principal characteristics of the single module are shown in Fig.2 and Tab.1,respec⁃tively.

Fig.2 Perspective view of the module

Tab.1 Parameters of a single module

2 Sensitivity analysis of the dynamic responses

In this chapter, a range analysis method has been done based on orthogonal experiments[29-30],which is a popular tool to do the sensitivity analysis.First of all,it is essential to make clear which factors should be studied and how many levels of these factors there are. Then, a proper orthogonal experimental rule can be determined according to the number of the factors and levels.Next,the ex⁃periments should be done in accordance with the rule arranged. Finally, the results are analysed and the most sensitive factors to the investigation indicators are found.

2.1 Orthogonal experiments

The purpose of the experiments is to study the effect of the arrangement of connectors. The common dual hinged connection arrangement is taken for example.As for the position configuration shown in Fig.3, there are three geometrical parameters (factors) to be determined. One of them is the interval between these two connectors,Hc,the other two areLcandVcthat represent the distanc⁃es between upper-hull and hinge points in longitudinal and vertical directions, respectively. Con⁃sidering the dimension of modules,three levels for each factor are set as shown in Tab.2.

Fig.3 Sketch of the dual hinged connection

Tab.2 Setting of factors and levels

From Tab.2,it can be seen that there are three factors with three levels to be considered in this paper and the orthogonal ruleL9(34) is the proper choice. As shown in Tab.3, 9 experiments could be arranged in this orthogonal experimental scheme for 4 factors at most, and each factor has 3 levels.

Tab.3 Orthogonal experimental scheme

whereXirepresents an index result of thei-th experiment.The index results could be the connector loads in three directions or the motions of modules.K1,j,K2,j,K3,jare the total index values of thejth factor at each level.The average index values are calculated as:

In order to obtain the sensitivity of each factor,the range value,Rj,of each factor has been cal⁃culated by Eq.(9).The bigger theRj,the more sensitive thej-th factor.

2.2 Analysis of sensitivity parameters

Through the normalized indices, the effects of each factor on the module responses and the connection loads can be assessed. Tab.4 lists the values of normalized indices. It is obvious that FactorA(horizontal spacingHc) is relatively sensitive to the sway, roll and yaw motions of the mod⁃ules in comparison with FactorsBandC. The numerical simulation has been conducted (not pre⁃sented here) to study how FactorAaffects the responses of sway, roll and yaw, and it is found that all the three responses tend to be reduced monotonically when FactorAincreases. It is reasonable because the increase of horizontal spacingHccan enhance the whole platform rigidity in these three rotational degrees of freedom. In this regard, FactorAshould be set as large as possible. FactorB(longitudinal directionLc) is insensitive to all the responses. The reason may be that the length of the module is much longer thanLc, so that the change ofLcbarely influences the responses of mod⁃ules and forces of connectors.For the surge,heave and pitch motions,FactorC(vertical distanceVc)is the most sensitive factor.By inspecting the numerical results,we can see that these three respons⁃es of modules are monotonically decreasing with the increase ofVc. Thus,Vccan be set at the 3rd level for the later optimized analysis.

Tab.4 Normalized indices of sensitivity parameters

As for the connection loads, only FactorAplays the most important role. The differences of connector forces between the maximum and minimum are 66.9%and 43.5%inxandzdirections re⁃spectively. In addition, the extreme force of the connectors is even bigger than 108N. It should be noted that the connector loads are also dependent on the number of connectors used to share the loads,which will be studied later.

All in all, the parameterLcseems insensitive to the responses of modules and connector loads.The parameterVcis only sensitive to the surge, heave and pitch motions, and should be set at the 3rd level due to its monotonic feature. The horizontal spacingHcis sensitive to the sway, roll and yaw motions of the modules.Since the relationship between FactorAand these responses are mono⁃tonic,thus the increase of the horizontal spacingHcshould be beneficial in terms of the reduction of the three rotational motions. Besides that, the increase of FactorAcan also reduce the connector loads. Based on the above discussion, the indices of the responses of modules are excluded in the later optimization model for simplicity. The connection loads depend on both the horizontal spacing and the number of connectors employed,which should be mainly investigated in the next chapter.

3 Optimization of connector arrangement

Based on the above discussion, this chapter mainly focuses on the influence of the horizontal spacing and the number of connectors employed on connector loads. According to the structure of modules,the connectors will be symmetrically distributed about the center of the end face of a mod⁃ule.Thus various connector layouts can be described by a parameterQ,which is the number of dis⁃tributed connectors from the center to the end edge of the module.

For each pair of adjacent modules, there are 2Q-1 numbers of positions to place connectors in line, and the horizontal spacing of adjacent connectors is the same. Fig.4 shows an example ofQ=3. Designers can determine whether to place a connector into the posi⁃tions (the red spots represent installed connectors)where the connectors should be symmetrically distributed along the central axis. Therefore, there are six scenarios of the connector layouts. The total arrange⁃ments can be numbered by 2Q-2 cases (excluding the single hinged connection at the center of a module).

Fig.4 Scenarios of connector layouts for Q=3

Fig.5 shows the three evaluation indices for all six layouts illustrated in Fig.4. All the indices inydirection are relatively small and flattened in comparison with that in the other two directions.It means whatever the layouts of connectors are, the indices are not significantly affected, indicating that the layout forms are insensitive to the loads in theydirection.Looking into Fig.5(a)and(b),it is interesting to find that the layouts (C-1, C-2) where connectors are centrally located in the middle may cause larger maximum load of a single connector and larger total connection loads in the bothxandzdirections. Differently, for the layouts of connectors arranged in two end sides, the total loads inxandzdirections seem to increase with increasing numbers of connectors, while the maximum loads of connectors inxandzdirections seem to decrease because the connectors commonly share some of the loads. For the load differences shown in Fig.5(c), it is obvious that the peak values al⁃ways appear when a connector is located in the middle position.The results suggest that a good lay⁃out design should avoid placing connectors in the middle of the end faces of modules. Furthermore,the peak values of the load difference tend to be smaller as the number of connectors increases.

Fig.5 Indices of connector loads for all layouts when Q=3

Generally, there seems no a standard archetype for the connector layout that can make all the load indices the best simultaneously.The design has to be compromised among the indices.An ide⁃al connector layout is very much dependent on specific engineering constraints and requirements as well as the preference of designers.For example,the index of total loads of connectors can be set as the maximum allowable constraint for satisfying the structure strength requirement of modules and the rest indices can be set as optimization goals. Similarly, the index of the maximum loads of con⁃nectors can be set as a designed load for the connectors. In this regard, the maximum loads of con⁃nectors are treated as a constraint condition in an optimization process. If designers prefer to make the load level among the connectors even, the designer can assign more weight on this index in an optimization process. In what follows, an optimization method will be introduced to determine the layout of connectors,where a multi-objective optimization will be utilized.

3.1 Optimization model for connector layout

The objective function of the optimization is associated with the three indices：the total connec⁃tion loads,the maximum load of connectors and the difference between the maximum and minimum loads inx,yandzdirections. To make the indices comparable at an equal level, all the terms should be normalized by dividing their extreme values,given by

in which the symbolsa,bandcdenote the weight coefficients for the three indices (multiple objec⁃tives).The assigned values for the weights of the objectives should reflect the decision maker’s pref⁃erences[35], which will be discussed later. The limited loads,Fdlim, is set for connectors, which is a maximum allowable load for all the connectors.

3.2 Optimal layouts and discussions

In numerical simulations,a three-modular floating system is considered.The connection loads are computed at a wave incident angle of around 85°[21]since the extreme loads usually occur at this angle. Furthermore, the optimal layout largely depends on the weights of objectives. Thus different weight combinations are included for different scenarios in engineering requirements.

The next section presents how to set up the weights for optimal layout. As shown in Tab.5,there are basically four groups of weights to be considered. These four groups of weights can be treated as four strategies respectively, which are equal strategy, total load strategy, maximum load strategy and cost effective strategy. The first strategy reflects that each objective has an equal con⁃cern. The second strategy imposes the preference on the total loads with more concern (60%) than other two objectives (40%).In other words,more concerns are given to the structural strength of the module’s end face. The third strategy gives more concerns on the load capacity of a single connec⁃tor(60%)than on the total loads(20%)and differences(20%).This kind of strategy can help design⁃ers to reduce the design load of connectors.The fourth strategy assigns 60%weight on the differenc⁃es and 20%weight for other two objectives respectively,which means that the designers can reduce the number of connectors in use for the cost effectiveness.

Tab.5 Weight coefficients and final optimal results

In order to satisfy engineering safety concerns, upper limited loadsFdlimfor the connector are set as optimization constraints. The numbers of connectors to be used are also confined. In numeri⁃cal simulations,there are 3 levels for the maximum allowable loadsFdlim= 1×108N,7×107N,4×107N; and for the position parameterQ=10, 7, 4. As shown in Fig.6, the optimal layout of each strategy is clearly presented. The vertical coordinate represents the scenario numbers of the weight combinations (strategies), and the horizontal coordinate denotes the position number for connectors.The red grids represent the positions of installed connectors and the blank grids represent no con⁃nectors installed. The quantitative results of the optimization are illustrated in Tab.5 forQ=10,where the maximum loads of connectors are listed in last three columns for all scenarios, while the resultant connector layouts are shown in Fig.6(a). The optimal results suggest that the connectors should be typically distributed on the two end sides, and not arranged in middle for the cost effec⁃tiveness. Different weight strategies lead to different layouts which will also be subject to the limit⁃ed load. For the equal strategy (scenarios number from 1 to 3), the number of required connectors mainly depends on the level of limited loads, and so is the total load strategy (scenarios number from 4 to 6). When the limited load is decreased, the required number of connectors has to be in⁃creased to jointly undertake the loads. However, for the maximum load strategy (scenarios number from 7 to 9), each side is arranged with four connectors. In this arrangement, the maximum loads of connectors can be significantly reduced as shown in Tab.5.For the cost effective strategy (scenarios number from 10 to 12),all the individual connectors are desired to perform in the upper of capacity within the limited load. To do so, designers can achieve the minimum number of connectors in use for module connection.The number of the employed connectors decreases when the limited load in⁃creases. Similarly, Fig.6(b) shows the layouts forQ=7. However, the maximum loads of connectors forQ=7 are larger than that ofQ=10,because the spacing between the adjacent connector positions is bigger. Finally, the layout whenQis set as 4 shown in Fig.6(c) will be examined. Apart from the red grid rows,those completely blank rows (scenarios number:3,6,9,12)indicate that there are no solutions as the limited load is set too small.These results suggest that the designer needs to adjust the limited load or the position parameter.

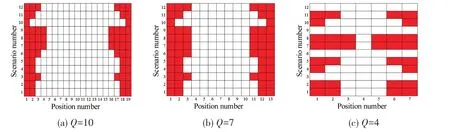
Fig.6 Optimized connector layouts for Q=4,7,10

Fig.7 Optimized connector layouts for Q=10,Hs=5,7.5 m

For the purpose of verifying the viability of the proposed optimization strategy, two other sea states are considered (Hs=5, 7.5 m andTP=12.4, 15 s, respectively). As shown in Fig.7, the optimal layouts are basically same as the results in Fig.6(a). The differences appear at the maximum load strategy when the sea state becomes tougher.The total loads and load differences may also increase when the big wave occurs,so that optimization procedure limits the number of connectors.If design⁃ers want to further emphasize the importance of the maximum load of a single connector, its weight of the maximum loads could be further increased. For other strategies, the optimization results are consistent with the previous ones.

In order to examine the superiority of the optimal results,a comparison has been done between the optimal layout(named as‘opt’)and a common layout(named as‘com’)for a dual-hinged con⁃nection in which the horizontal spacing of the connector equals to that of the module’s col⁃umns[26–28].The optimal layout is generated from the equal strategy with a limited load of 1.0×108N.This strategy leads to an optimal layout that employs four connectors. For a fair competition, the third layout that has the same number of connectors as the optimal layout is also added for compari⁃son. The connectors of the third layout are evenly distributed on the end face with equal spacing,named as‘eve’connection.

Fig.8 Comparison among the optimized layout,even layout and common layout

The results are shown in Fig.8,where the loads inydirection are excluded because they are in⁃sensitive to the layout design as mentioned before.Fig.8(a) and Fig.8(d) show the total loads,where the optimal results are obviously better than the results of the other two.Especially for the peak,the optimal layout has a reduction of about 30% of the total load inxdirection than that of the common layout. As shown in Fig.8(b) and Fig.8 (e), the maximum loads of connectors for the four connec⁃tors’layouts (‘opt’and‘eve’) are smaller than that of the common layout, because the extra con⁃nectors can jointly share more loads of the connection. However, the maximum load of the optimal layout also has about 50% reduction compared with that of the even layout, which proves that the loads of connectors depend on both the connector number and the position of connectors. Similarly,Fig.8(c) and Fig.8(f) show that the load differences among the connectors are consistent with what has been expected. The optimal layout has the smallest load difference among these three layouts,because the connectors are distributed on both of the end sides. However, the even layout has the biggest load difference, because there are two connectors arranged in middle. Since these two con⁃nectors only bear very small loads, the load differences of four connectors are enlarged. From this comparison study, the benefits of this proposed method can easily be seen. The method enables to carry out a tough analysis covering many involved factors to determine the most reasonable layout for connectors.

4 Concluding remarks

Connectors are key components for modular VLFSs. The connection of floating modules seems simple but the underlying mechanism is actually complicated. A configuration of connectors could significantly affect the performance of the floating system. Many factors could alter the relationship between connector layouts and the dynamic responses of modules and connectors. Under the com⁃plex influence of these factors, precise prediction of the effect of connector layout is not simple, so how to design a reasonable connector layout has not been well solved. This paper presented an in⁃clusive approach to determine the optimal layout for connectors.Firstly,the connected modular sys⁃tem was modeled by the network modeling method. A sensitivity analysis was conducted to under⁃stand the relationship between the location of the connector and the dynamic responses of modules and connectors, and further to find the most influential factors. Then an optimal assessment model was established with consideration of engineering concerns,constraints and designer’s preferences.In numerical studies, a three-modular floating system was considered for the optimal connector’s layout based on different decision strategies. Numerical evidences suggest that connectors should be located at the far end sides of modules for the load reduction,and not in middle for cost effective⁃ness. The proposed method enables designers to flexibly design the connector layout according to preferences on engineering concerns and provides designers a scientific tool to more freely deal with the complicated situations where experience and intuition may be invalid.