航天器非线性动力学专业课程中分形维数的概念教学设计
2022-06-18代洪华谢丹岳晓奎朱战霞
代洪华 谢丹 岳晓奎 朱战霞



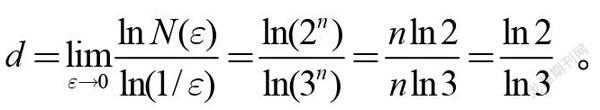
DOI:10.19980/j.CN23-1593/G4.2022.17.019
摘 要:文章针对西北工业大学的航空航天专业航天器非线性动力学研究生课程的分型维度这一重要专题,围绕其教学设计、教学过程、教学思路和教学效果分析等进行创新,探索性地对航空航天类专业课程教学进行改革,旨在将创新思维培养、创新能力塑造的理念融入工科专业课程中,达到“如盐在肴,融于细微”的效果。文章所提出的教学设计方法将对推进西北工业大学专业课程实践具有重要引导作用。
关键词:教学设计;航空航天;专业课程;分型维度
中图分类号:G642 文献标志码:A 文章编号:2096-000X(2022)17-0076-04
Abstract: This paper focuses on the innovative teaching design of the concept of Fractal Dimension in an aerospace major course, Spacecraft Nonlinear Dynamics, in Northwestern Polytechnical University. Upon centering around the innovations during the phases of teaching design, teaching process, teaching concept, and teaching effect assessment, the teaching methodology of this aerospace major course has been explored and reformed, with the purpose of insensibly adding cultivation of innovative thinking and creative ability into the teaching process. The proposed teaching design methodology is promised to push forward reform process of the major course of Northwestern Polytechnical University.
Keywords: teaching design; aerospace; major course; fractal dimension
一、教学设计思路
混沌理论被誉为20世纪科学界最伟大的三大理论之一,与相对论、量子力学并列。混沌理论是非线性动力学研究生课程的核心内容,涉及的科学内容非常丰富。其中一个重要知识点是“fractal”即“分形”,分形的数学基础是分形维数。分形理论认为空间维数是可以连续变化的非整数。该观点跟学生接受的传统欧几里得整数维数不同,带来教学中的讲授、理解难度。
本节课遵循科学研究的思维方法,采用“提出问题-分析问题-求解问题-推广应用”的思路,进行分形维数概念的学习,为深入学习分形几何奠定基础。首先,从计算规则几何形状的维数出发,扩展到如何计算某些特殊几何形状(分形)的维数,引发学生关于维数定义的思考。其次,将问题抽象成数学模型,通过对规则几何物体维数的分析,引出维数的传统定义方式,先从已有知识入手,进而将其推广到分形图形上,并解释了自相似维数、盒维数等分形维数的数学意义。再次,通过对一些分形几何图案的深入分析,强化了对分形维数概念的理解。最后,通过展示维数在分形几何领域的应用,阐明维数的科学及应用价值,引导学生理解维数的内涵。
课程难度安排上由浅入深,让学生易于接受分形维数这一颠覆性的概念。课程结合Matlab、Mathematica、Geogebra等数学软件进行演示,实现了抽象数学概念的形象化展示,以达到多层次教学的目标。
二、教学过程
(一)问题的提出
1967年,國际权威期刊《Science》杂志上发表了一篇划时代的论文,它的题目是《英国的海岸线有多长?统计自相似性与分数维数》。该论文揭开了分形维数的研究序幕。一种新的科学理论的提出,往往是在归纳现有的理论的基础上,进行适当的推广与引申而得到的。为了引导学生主动思考,在课程的开始,首先抛出一个与“英国的海岸线有多长?”异曲同工的问题:从远处观察一根毛线,是一维的线。再细看,它是三维柱体。再近一些,观察毛线上的纤维,又是一维的线。再靠近,则纤维又变成了三维柱体。如此循环往复,发现维数竟然是随着观察尺度的不同而变化的,这似乎打破了日常的认知,那么究竟应该建立怎样的数学模型来描述维数的特征?如何得到维数明确的结果呢?
(二)拓扑维数的局限
力学的学习是一个循序渐进的过程,需要从基础知识讲起,才能做到深入浅出。为了实现对以上问题的分析,首先得从拓扑维数讲起。拓扑维数表示描述一个对象所需的独立变量的个数,是人类认识世界的最原始的维度概念。比如描述光滑曲线上一个点的位置,所需的独立变量个数为1,即当前点与参考点之间的距离,因此光滑曲线的拓扑维数为1。更进一步,在平面上确定一个点需要两个坐标,因此正方形、圆、椭圆等平面图形的拓扑维数是2。在三维空间中确定一个点需要三个坐标,因此立方体、球体等立体图形的拓扑维数是3。
通过抽象出几何对象的数学模型,找到了计算一般几何图形拓扑维数的方法,但是这种方法是否通用?此时,为了引导学生认识到拓扑维数的不足,引入一种新的几何图形——Cantor集,如图1所示。三等分一条线段并挖去中段,再把剩下的两段同样三等分并挖去中段,如此无限地进行下去,得到由无穷多离散的点组成的Cantor集。可以借助数学软件Mathematica向学生动态演示Cantor集的生成过程。
记初始的线段为S,第n次迭代得到的图形为S,S的所有线段长度之和记为L,则L=1,L=2/3,…,L=(2/3),…,L=0。通过总结长度的变化规律,得出结论:无限迭代下去,最终Cantor集的长度将为0,即无限多个点集中在长度为0的区间内,无法用拓扑维数解释其结构,因为它的拓扑维数既不是0也不是1,这显然与我们的常规认知相违背。通过这个例子,我们看到拓扑维数的定义有一定的局限性。
之所以出现这种现象,是因为Cantor集比常见的几何图形更加“复杂”,而我们依然尝试用拓扑维数来分析这一“复杂”的几何图形。对于Cantor集,既然其拓扑维数无法通过计算得到,那么该如何定义新的维数来描述它?此外,可以看到拓扑维数一定是整数,那么这种新的维数是否可能不是整数?
(三)分形维数的概念
1. 自相似维数。事实上,Cantor集的复杂之处在于,它是对自身进行迭代而生成的,具有一定的自相似性,即局部与整体具有相似性。为了对自相似维数进行描述,先给出自相似集的定义:设A是一个有界集,若A可以分成多个相等的且与A相似的部分,则称A为自相似集。
通过举例,进一步说明通常所用的整数维已不足以用来描述分形,难以描述各种集合充满空间程度的不同,也难以对比两个不同分形集的复杂程度。所以,需引入自相似维数。每一个自相似集都对应一个自相似维数,这个维数一般不是整数的,但对有些特殊的分形集,其维数也可以是整数,比如希尔伯特曲线。
2. 盒维数分形维数有多种定义,上面自相似维数只是其中一种,只适用于自相似图形。一般来说,分形维数的计算方式复杂,应用不同的定义计算维数也不尽相同。
下面是Hausdoff关于维数的定义:在数学上,对于m维空间点集A,记N(ε)是覆盖A所需的半径为ε的m维球的个数,则当ε>0时,如果N(ε)的增长规律服从N(ε)正比于ε,就称点集A的Hausdoff维数为d。
Hausdoff维数需要用到较为复杂的测度理论,计算复杂很少被采用。在实际使用中,经常用到的一种维数是盒维数,它能够通过实验近似地计算出,在一些比较规则的集合上,盒维数与Hausdoff维数是相同的。
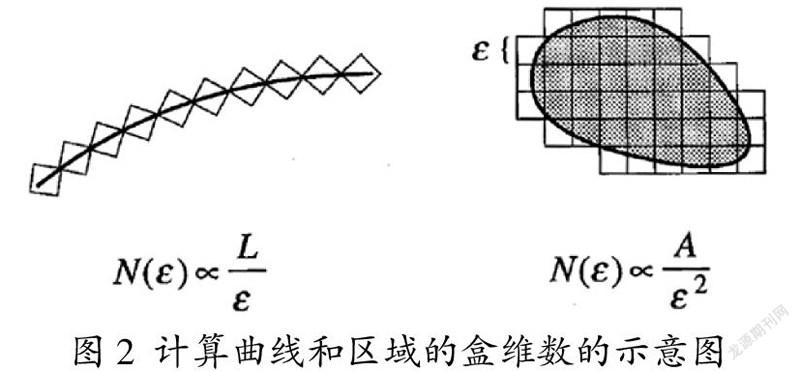
盒维数的通俗解释如下:直观地,从“铺砌”的角度看,用边长为ε的正方形覆盖某对象(曲线或区域),最后数出所使用的正方形数目N,改变ε的大小,自然会得到不同的N值,如图2所示。通常ε越小,需要的N
在实际使用中,常用盒维数作为分形集的维数,因为盒维数方便近似计算。方法是:根据实际问题的背景和尺度选定ε值的一个合适范围,并数出相应的N,作ε与N(ε)的双对数图,由其斜率来近似估计盒维数。为了加强学生对于盒维数的直观理解,下面举出几个计算实例。
(1)Cantor集
用长度为ε=(1/3)的线段覆盖第n次迭代的结果S,需要N=2个这样的线段,因此Cantor集的盒维数为:
Cantor集是自相似集,可以发现其盒维数与自相似维数相等。
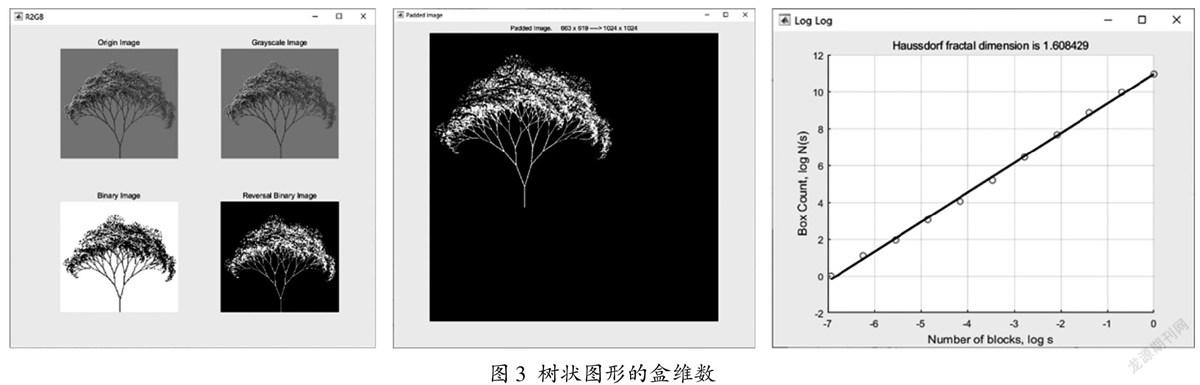
(2)计算图3中图形的盒维数
由于这个图片(图3中间图)比较复杂,很难判断其是否具有自相似性,也不能通过手算的方式得到盒维数,可以根据盒维数的定义,借助计算机辅助计算,具体的算法流程为:
第一步,图片预处理,把RGB图像二值化,并把图片的宽度和高度(像素数)增广为2的n次幂,以方便后面的计算;第二步,设置正方形的边长ε为图片的宽度(自然,用这样的正方形覆盖原图,需要N(ε)=1个);第三步,计算N(ε);第四步,如果ε>1,则令ε∶=ε/2,即把正方形的边长减半,并重复第三步;第五步,画出log(N)和log(1/ε)的曲线,并线性拟合,直线的斜率即原图形的盒维数。在Matlab中编写计算盒维数的程序。除了手动编写程序,Matlab的工具箱FracLab也提供了计算盒维数的功能,其算法流程和本文相同,可以在课堂上介绍FracLab的使用方式,增强学生的动手能力。
(四)课后思考
分形维数的课堂教学,得到学生的普遍好评。其关键在于分形维数这个概念是对学生传统思想的冲击,与此同时又与自然界事物密切联系,称得上是“来源于自然,凝结于思想”。几何起源于对自然界物体的抽象,规则几何是理想化的产物。为了充分地认识自然,人们提出了分形几何理论。分形几何从创立之初,就与自然界物体密切相关,为人类认识更加复杂的自然界物体提供了新的数学工具。
分形几何创始人Mandelbrot猜想,自然界的许多东西都是由重复简单步骤而产生出来的,这就能够解释一些让人们困惑的现象。正是因为它们具有自相似性,使得它们的维数不再是整数,也使得它们更能充分地充满在空间中。由此可见,生命的演化早已打破整数维的限制。
宇宙是否是一个分形?太阳系是一种最基本的结构,无数个这样的基本结构形成了涡旋状的银河系,银河系与太阳系有着相似性,再进入上一层,这些涡旋状的银河作为构成元素进一步形成更大的涡旋状银河系,最终形成宇宙。如果宇宙是一个分形,那么它的分形维数应该是多少?
三、小结
分形维数是分形理论的重要概念,它们突破了传统欧氏几何的局限,为理解更复杂的几何图形提供了有效的工具,维数的定义也是分形几何的基础,对日后学习分形几何和非线性动力学有着较大的帮助。本节课按照科学研究的一般流程,遵循科学研究的思维模式,先从现实问题出发,分析传统维数定义的局限性,引导学生一步步发现问题,引出分形维数的概念。之后,阐明了自相似维数與盒维数这两个重要的概念,并且通过例题进一步巩固所学的知识。最后,介绍分形维数的简单应用,引发学生对分形与自然界之间联系的思考,使学生在学习知识的同时,培养科研的思维方法,达到教学效果的升华。
四、教学效果分析
通过在非线性动力学课程上,对西北工业大学航天学院2020级秋季博士生实施以科学研究的思维方法为导向的课程设计方案,从课堂效果和课后反馈,以及综合分析作业和考试情况,看出本节关于分形维数概念的教学设计,完成了课程知识的传授,提升了教学质量,基本实现了教学改革的目标。首先,先从实际问题中提炼出维数的概念,让学生明晰维数的研究背景,进而提到拓扑维数的局限性,层层铺垫,使得分形维数这一新概念呼之欲出,充分调动了学生的兴趣,也让学生明确了提出科学问题的一般过程。其次,从分析几个简单的自相似集的维数入手,由浅入深,循序引出自相似维数与盒维数的概念,并且穿插讲授各种维数之间联系与区别,让学生了解分析科学问题的一般方法。再次,在所学知识的基础上补充例题,不仅丰富了学生对分形图案的认知,也锻炼了学生计算分形维数的能力。最后,通过思考分形与自然界以及人生的联系,明确了分形维数的研究意义与应用价值。科学研究的思维方法串联了各个教学环节,贯穿于整个教学过程。采用该教学设计,学生不仅掌握了基本思维方法,还提高了对新知识的探索欲望,锻炼了综合能力,为学习其他课程以及科研工作奠定了基础,达到了举一反三、寓教于乐、理论结合实践的多重教学效果。
参考文献:
[1]林若波.“混沌式”专业课程体系的构建[J].教育与教学研究,2010(24):109-112.
[2]李元杰,汤正新.如何给工科学生讲分形物理——介绍华中科技大学非线性物理教学改革之一[J].物理与工程,2001(3):17-19.
[3]胡海岩.对力学教育的若干思考[J].力学与实践,2009(31):70-72.
[4]丁虎,陈立群.本科生振动力学课程教学探索与建设[J].教育教学论坛,2020(34):267-268.
[5]徐建光.坚持全课程育人深化课程思政改革[J].上海教育,2017(12):14-17.
基金项目:2020年度国家自然科学基金面上项目“空间旋转非合作航天器柔顺消旋动力学与控制”(12072270)
作者简介:代洪华(1986-),男,汉族,山东聊城人,工学博士,教授,博士研究生导师,研究方向为空间操作。
