含负顾客的M/M/1两种休假体制的排队系统的平稳性态
2022-06-17闫俊娜杨永燕
闫俊娜, 杨永燕
(1.林州建筑职业技术学院 基础教学部,河南 林州456500; 2.安阳学院 数理学院,河南 安阳455000;3.濮阳石油化工职业技术学院,河南 濮阳 457000)
0 引言
半休假策略(也称为工作休假)的排队模型在现实生活中应用非常广泛,如银行休假不是工作人员完全休息,而是部分人员仍继续值班.对于半休假策略的研究已取得丰富的成果[1-5],例如:Ye等[2]考虑M/M/1/SWV+MV,运用两种方法得到队列长度的平稳分布,推导出平稳队列长度和客户逗留时间的随机分解结果;Kumar等[3]研究了多个工作休假的有限批量到达或服务队列瞬态行为的数值.实际上,在半休假策略的排队模型中还常会遇到外来对服务系统实施的援助——负顾客,他们的到来会抵消掉正在被服务的正顾客.针对此,Panda等[6]研究了具有正面和负面客户以及多个工作假期的单服务马尔可夫排队系统,得到4种情况下积极顾客的均衡策略和社会效益.薛红等[7]考虑一个具有Bernoulli休假和负顾客到达的离散时间Geo/G/1早到达重试排队系统,利用马尔可夫链法和补充变量法推导出系统演化的平衡方程组,得到嵌入马尔可夫链的平稳分布和一系列排队指标.岳德权等[8]考虑由负顾客到达引起服务台故障从而进入修理期的排队系统,研究了负顾客到达引起的系统服务速率变化.
为节约系统工作量相对较少时的运行成本和能耗,本文在经典排队系统M/M/1中添加负顾客到达,研究两类顾客(正顾客、负顾客)、两种休假体制(单次工作休假(半休假)体制与多重休假体制(M/M/1/SWV+MV))下的M/M/1系统.从实际应用的角度来看,本研究可用于服务系统维护模型的建模.当工作量相对较少时,服务系统首先进入一个缓冲期(工作休假),其间以较低的速率工作.在缓冲期结束后,服务系统中如果有客户,则恢复到正常的服务状态,以获得更多的利益;否则,服务系统进入休假期进行维护.
1 模型描述
1)顾客到达:系统包含正、负两类顾客,分别以参数为λ+、λ-的泊松过程到达并形成等待队列.
2)若系统中有正顾客,则到达的负顾客一对一抵消掉正在接受服务的正顾客;若系统中无正顾客,则负顾客自动消失,且该类顾客不接受系统服务.
3)正常服务周期的服务机制:系统以服务率为μb的指数分布服务顾客.
4)工作休假(半休假)周期的服务机制:系统以较低的服务率μv(μv<μb)为到达顾客提供服务,而不是完全停止服务.
5)服务、休假机制:正常休假与工作休假.
正常休假期间不向任何新来顾客提供服务,即停止服务;工作休假(半休假)模式,即在一个正常服务期结束后,服务系统会以较低的速率服务顾客,而不是完全停止服务.当一次工作休假结束时,若服务系统中有新顾客,则恢复正常服务;否则,进入正常休假模式.当正常休假结束时,若服务系统中无顾客,则再次正常休假.以此类推,直到正常休假结束时,系统中有新顾客到达,才开始正规的服务期.
6)正常休假时间服从参数为θw的指数分布.
7)工作休假时间服从参数为θv的指数分布.
8)假设正常服务期的到达时间间隔、正常服务时间、工作休假期的服务时间、工作休假时间、正常休假时间均相互独立.
9)系统服务机制为先到先服务机制.
2 模型的拟生灭过程
设Q(t)为t时刻排队系统中的顾客数(排队队长),定义

则{Q(t),J(t),t≥0}是一个马尔可夫过程,其状态空间为Ω={(0,0),(0,1)}∪{(k,j):k=1,2,…;j=0,1,…}.系统状态按照字典序列排列后,得到分块的马尔可夫过程的无穷小生成元Q的分块形式
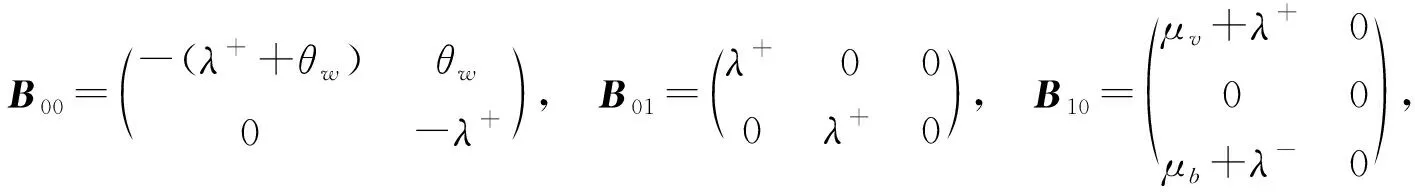
可见,由矩阵Q的结构可知马尔可夫过程{Q(t),J(t),t≥0}是一个拟生灭过程.
3 系统稳态下的队长分布
运用矩阵几何解的方法得到拟生灭过程{Q(t),J(t),t≥0}的无穷小生成元的稳态概率解[9]
其中πk指服务系统处于平衡后系统中有k个顾客的平稳队长的概率.
为了得到无穷小概率向量,在拟生灭过程中引入二次矩阵方程
R2B2+RB1+B0=0
(1)
的最小非负解——率矩阵R.
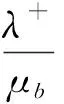
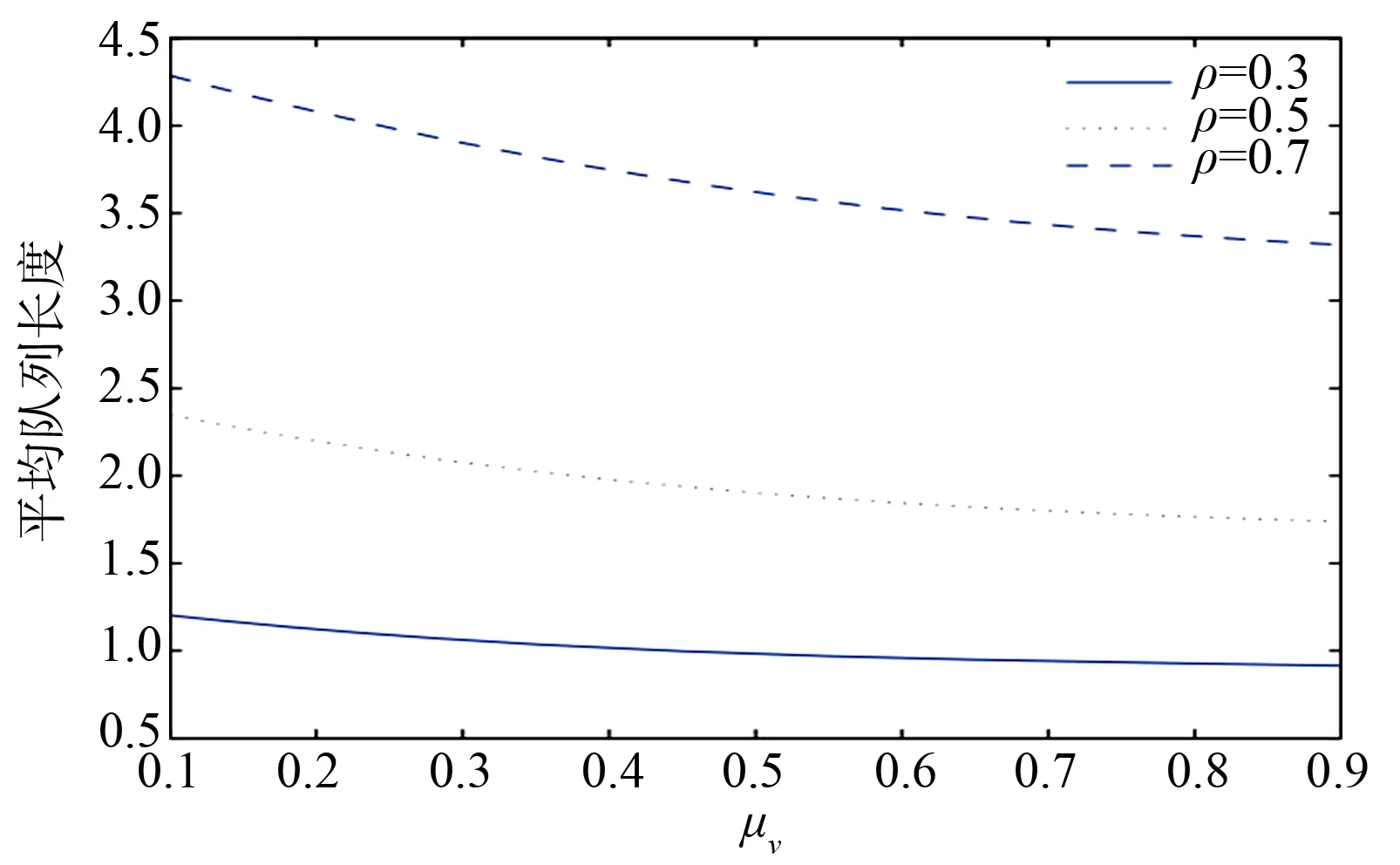
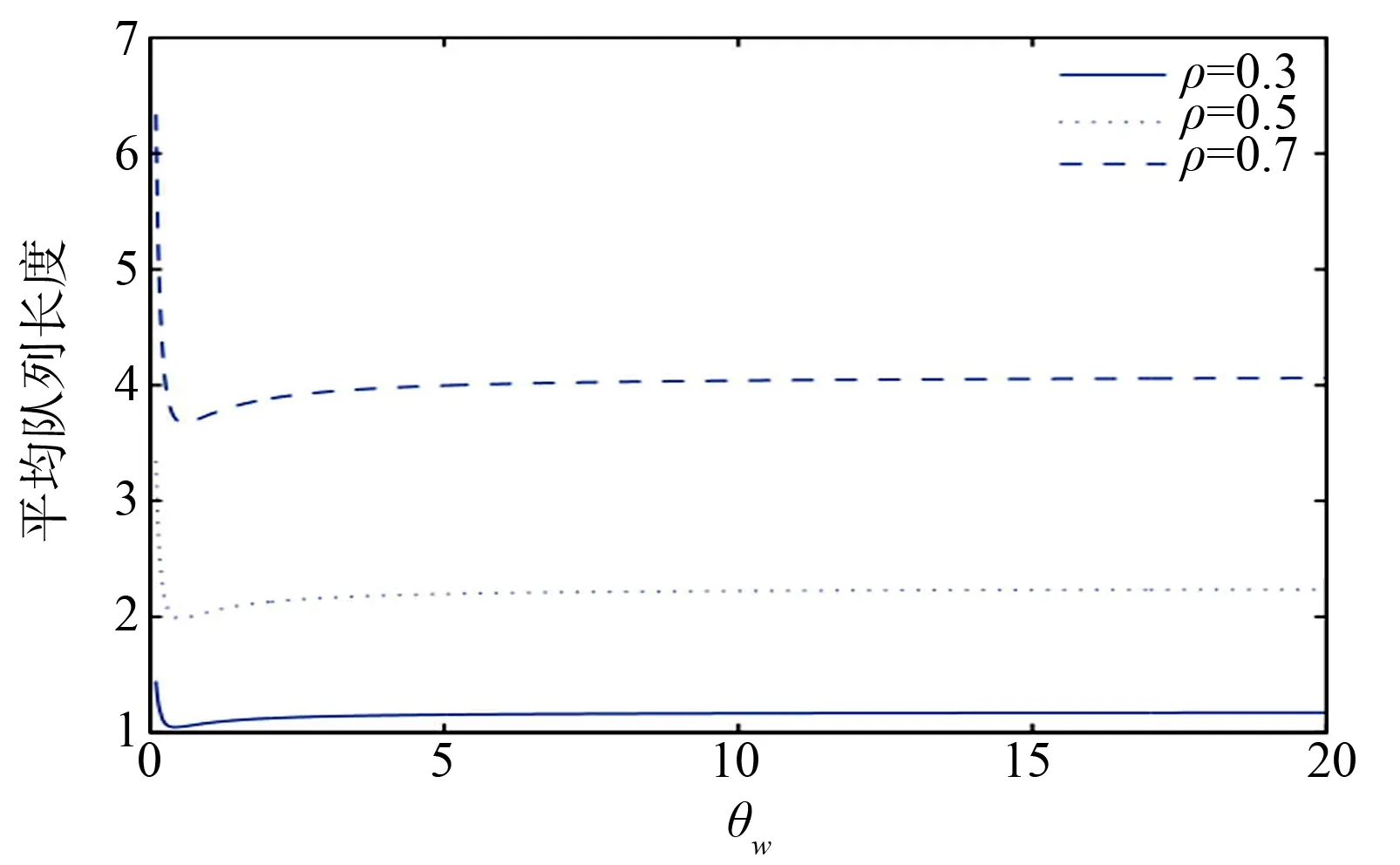
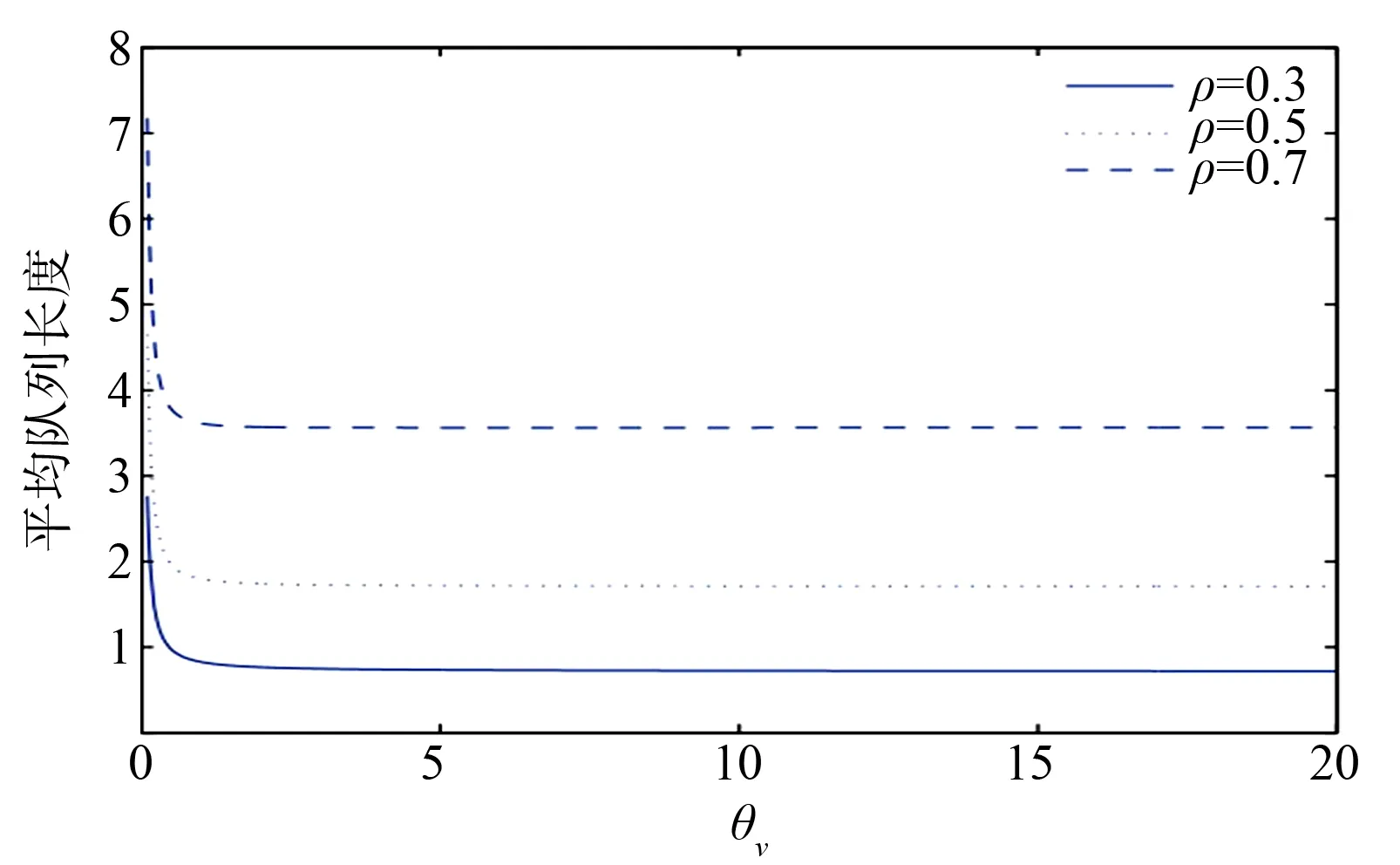
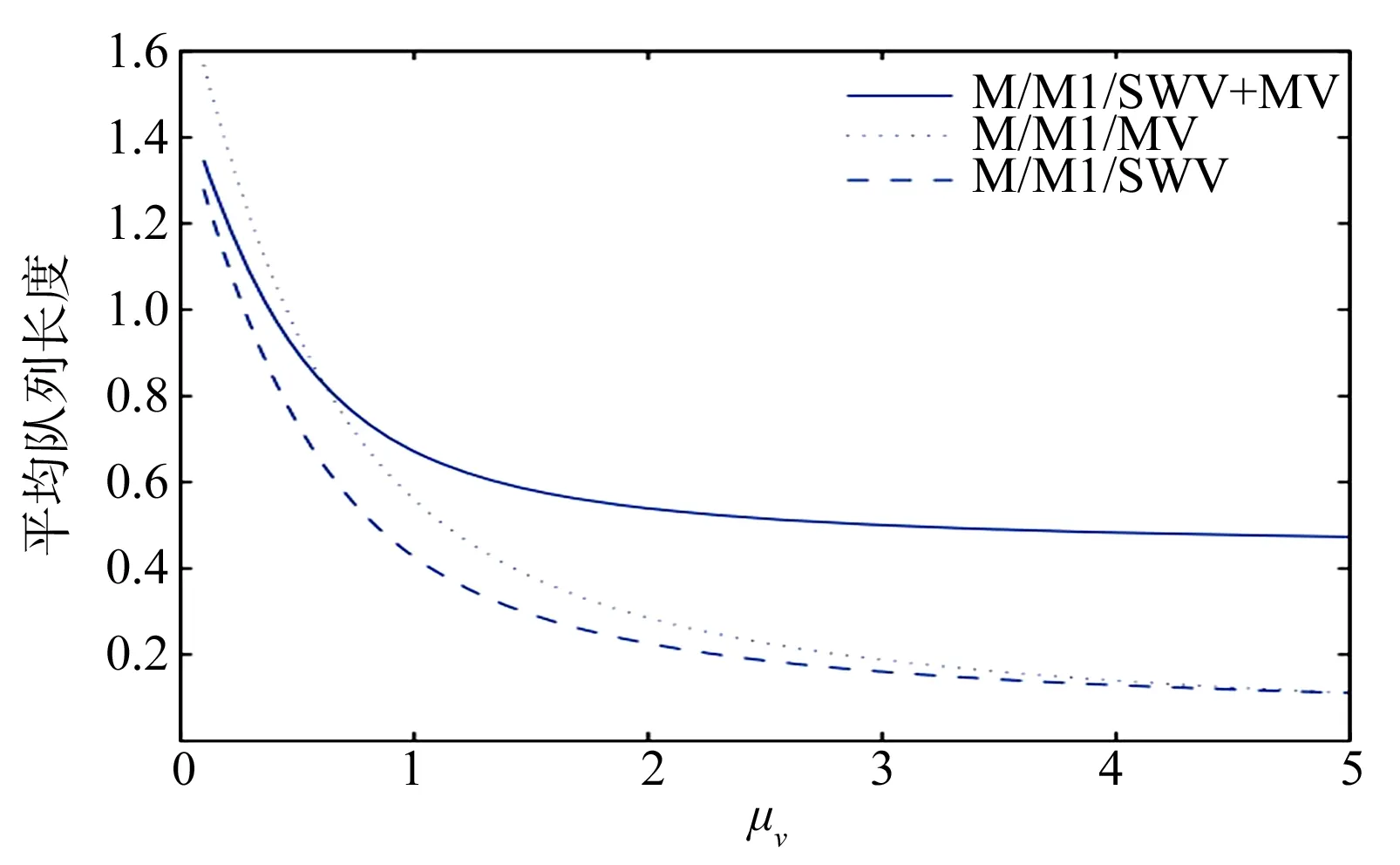
其中0 证由于B0+B1+B2,R是上三角矩阵,可假设 (2) 将R代入(1)式,可得 (3) 引理2r满足 证由方程组(3)可知(λ-+μv)r2-(λ++λ-+θw+μv)r+λ+=0,两边同时除以r,整理可得 引理3(π00,π01,π10,π11,π12)B(R)=0有如下正向量解: 其中π00是常数,可由归一化条件得出. 证由于 代入矩阵方程(π00,π01,π10,π11,π12)B(R)=0,可得下列方程组: 求解方程组,定理得证. 定理1拟生灭过程{Q(t),J(t),t≥0}是正常返的,当且仅当ρ<1. 证由文献[9]中关于复杂边界的无穷小生成元的改进方法可知,拟生灭过程{Q(t),J(t),t≥0}是正常返的充要条件为率矩阵的谱半径Sp(R)=min{r,β,ρ}<1,且线性矩阵方程(π00,π01,π10,π11,π12)B(R)=0有正解.由引理1与引理3可知,上述条件满足,当且仅当ρ<1. 定理2如果ρ<1,则马尔可夫链的概率分布为 证运用文献[9]中矩阵几何解的方法,可得 πk=(πk0,πk1,πk2)=(π10,π11,π12)Rk-1,k=1,2,…, (4) 由(2)式可得Rk-1,代入(4)式,假设π00可由归一化条件得出,即可得结论. 由定理2,可以得到稳态情况下的概率: 定理3服务系统在工作休假、正常休假期间,队长的条件概率的几何分布为 P(N=K|J=0)=(1-r)rk,P(N=K|J=1)=(1-β)βk,k=0,1,…, 其中N是稳态下的队长. 定理4在ρ<1和μv<μb的条件下,稳态队列长度Q可以分解为两个独立随机变量之和, Q=Q0+Qd, 其中:Q0是标准M/M/1队列在稳定状态下的队列长度,遵循参数为1-ρ的几何分布;Qd为额外的队列长度,由于受两种休假策略的影响,因此具有概率母函数 稳态平均额外队列长度 稳态平均队列长度 假设θw=0.3,θv=0.4,λ-+μb=1,此时ρ=λ+,绘制μv变化时的稳态平均队列长度变化趋势(图1).可以看出,随着μv的增加,稳态平均队列长度相应减少;且当其他参数固定时,ρ越大,稳态平均队列长度也越大.假设λ-+μb=1,μv=0.3,θv=0.4,绘制θw变化时的稳态平均队列长度(图2).可以看出,随着θw的增加,稳态平均队列长度收敛到固定常数.假设λ-+μb=1,μv=0.3,θw=0.3,绘制θv变化时的稳态平均队列长度(图3).可以看出,随着θv的增加,稳态平均队列长度收敛到固定常数. 图1 μv对稳态平均队列长度的影响Fig.1 The effects of μv on the steady-state mean queue length 图2 θw对稳态平均队列长度的影响Fig.2 The effects of θw on the steady-state mean queue length 图3 θv对稳态平均队列长度的影响Fig.3 The effects of θv on the steady-state mean queue length 假设λ+=0.5,λ-+μb=5,θw=0.3,θv=0.7,比较带单重工作休假的M/M/1/SWV队列、带多重工作休假的M/M/1队列(M/M/1/MV)和本文提出的M/M/1队列的稳态平均队列长度随μv的变化趋势(图4).可以看出,只有工作休假的排队系统,虽然随着服务率μv的增加,稳态平均队列长度下降较快,但对服务器的损耗较大;本文提出的排队系统,随着μv的增加,稳态平均队列长度减少,且对服务器的损耗相对较小,兼顾了服务器与顾客两方面,更为贴切实际.因此,服务公司可以根据实际情况,设计合理的休假和服务机制,使公司更灵活、更高效地运作. 图4 μv对不同队列稳态平均队列长度的影响Fig.4 The effects of μv on the steady-state mean queue length of different queue
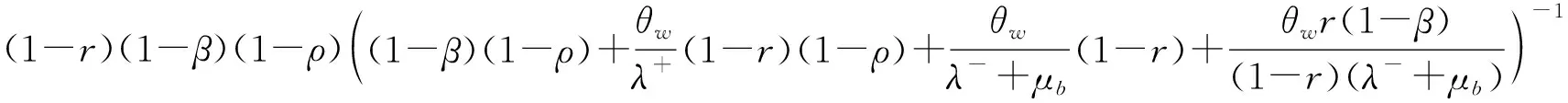
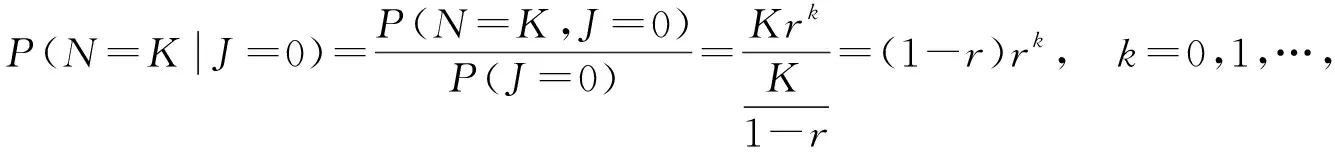
4 随机分解
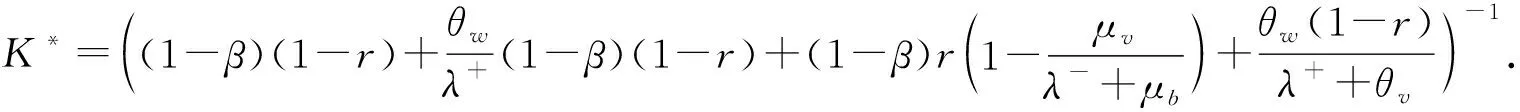
5 数值模拟