一类具有恐惧效应的Holling-Ⅲ类时滞捕食系统

张子振， 张伟诗

(安徽财经大学 管理科学与工程学院,安徽 蚌埠 233030)

0 引言

捕食者-食饵系统在现实世界中是一种非常普及的系统.为了揭示捕食者与食饵之间的动力学关系，在过去的几十年中，生物数学界学者对许多捕食者-食饵系统进行了研究，尤其是在两种群捕食系统方面取得了丰富的成果[1-5].2011年，Zanette等[6]研究发现，歌雀由于受到捕食者的惊吓导致繁殖率降低了40%.为了更好地描述环境因素对捕食系统的影响，Wang等[7]首次提出了一类具有恐惧效应的捕食系统.随后，具有恐惧效应的捕食系统受到国内外学者的关注[8-11].考虑到不同形式的功能反应对捕食系统的动力学行为的影响，韩梦洁等[12]提出了具有恐惧效应的Holling-Ⅲ类捕食系统

(1)

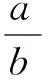
显然，捕食者种群捕获食饵种群后，须经过一个妊娠周期才能达到数量上的增长.因此，本文在系统(1)的基础上，考虑捕食者种群的妊娠时滞，研究如下时滞捕食系统：

(2)

其中τ为捕食者种群的妊娠时滞.

1 正平衡点的局部渐近稳定性和Hopf分岔的存在性

λ2+Υ1λ+Υ0+(Θ1λ+Θ0)e-λτ=0,

(3)

λ2+(Υ1+Θ1)λ+Υ0+Θ0=0.

(4)

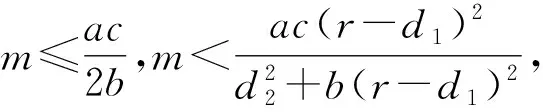
当τ>0时，假设λ=iω(ω>0)为方程(4)的根，则有

(5)

进而有

(6)

令ω2=χ，则方程(6)变为

(7)

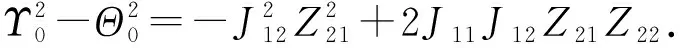
定理1当τ∈[0,τ0)时，系统(2)局部渐近稳定；当τ=τ0时，系统(2)在E*(x*,y*)处产生Hopf分岔，并产生一簇分岔周期解.

2 分岔周期解的方向和稳定性

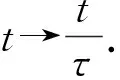
(8)

其中X(t)=(X1(t),X2(t))T∈C，且

F(ζ,X(t))=(τ0+ζ)(F1,F2)，

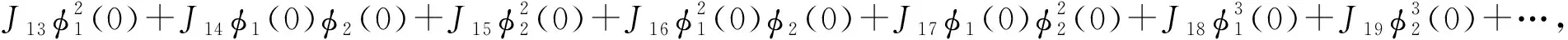
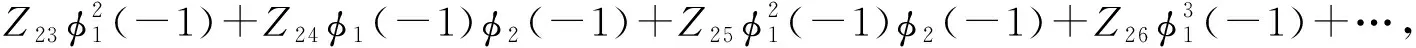
η(θ,ζ)=(τ0+ζ)(U1δ(θ)+U2δ(θ+1)),

其中，δ(θ)是狄拉克函数.定义

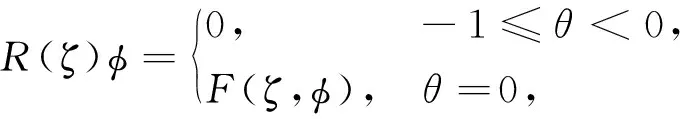
及

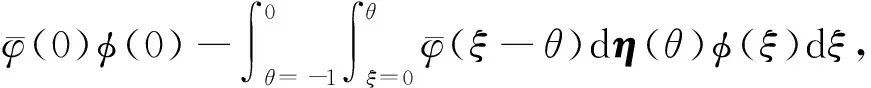
(9)

其中

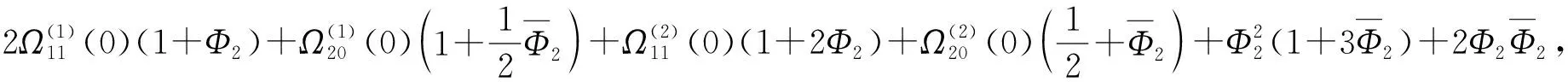
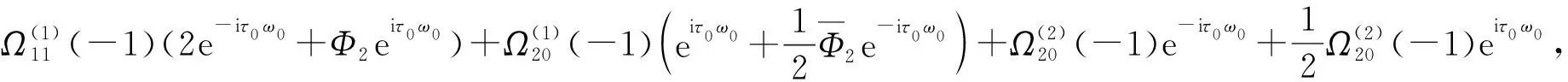
且

进而得到确定分岔周期解的方向和稳定性的系数

(10)

定理2对于系统(2)，当Γ1>0时，Hopf分岔是超临界的，否则，Hopf分岔是次临界的；当Γ2>0时，分岔周期解是不稳定的，否则，分岔周期解是稳定的.

3 仿真示例

在系统(2)中，选取r=0.6，K=0.1，d1=0.01，d2=0.011，a=0.1，b=0.47，c=0.5，m=0.045,计算得系统的唯一正平衡点为E*(1.248 9,5.162 0)，进而得到ω0=0.626 6，τ0=3.058 9.由定理1可知，当τ∈[0,3.058 9)时，系统局部渐近稳定,仿真效果如图1所示.当τ0>3.058 9时，系统不稳定，并在E*(1.248 9,5.162 0)处产生Hopf分岔,仿真效果如图2所示.另外，计算得λ′(τ0)=1.007 4-0.809 1i，C1(0)=-0.250 7+0.906 4i.根据公式(10)，Γ1=0.248 8，Γ2=-0.501 4.由定理2可知，系统在τ0=3.058 9处产生的Hopf分岔是超临界的，并且是稳定的.

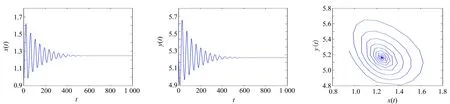
图1 当τ=2.587 7∈[0,3.058 9)时，系统局部渐近稳定Fig.1 The system is locally asymptotically stable when τ=2.587 7∈[0,3.058 9)

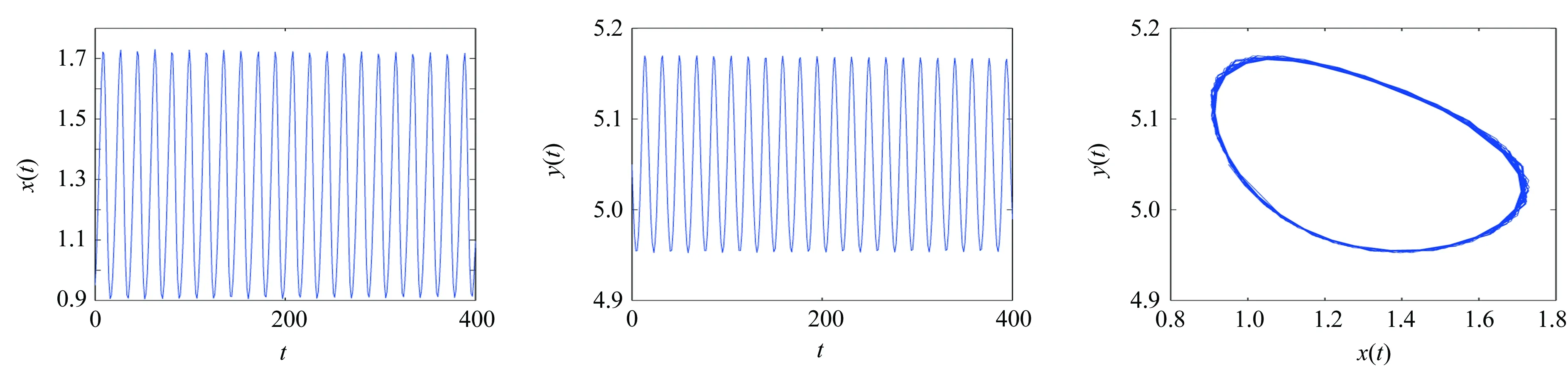
图2 当τ=3.424 8>τ0=3.058 9时，系统不稳定且产生Hopf分岔Fig.2 The system is unstabe and with Hopf bifurcation when τ=3.424 8>τ0=3.058 9

4 小结

本文考虑捕食者种群的妊娠时滞，研究了一类具有恐惧效应的Holling-Ⅲ类时滞捕食系统.以捕食者种群的妊娠时滞为分岔参数，推导出系统局部渐近稳定和产生Hopf分岔的充分条件，并计算出系统产生Hopf分岔的时滞临界值.研究表明，在一定条件下，当时滞τ∈[0,τ0)时，系统中的食饵种群和捕食者种群的数量趋于正平衡点，系统处于理想的稳定状态.当时滞τ越过临界值τ0时，系统失去稳定并产生Hopf分岔，食饵种群和捕食者种群的数量处于周期震荡状态，不利于自然资源的合理开发利用.此外，本文还利用中心流形定理和规范型理论研究了系统在τ=τ0处产生Hopf分岔的方向和分岔周期解的稳定性.