基于分形理论的直流系统环网接地故障检测方法研究

徐 强

(国网无锡供电公司，江苏 无锡 214100)

0 引言

经济的迅猛发展促进了电力负荷容量与组成成分的改变，直流负载的增长带动了直流系统的发展。为了保证重要负载供电的可靠性，常采用分段环网供电的形式，环网供电在提高支路供电可靠性的同时，也给接地故障检测带来了困难。低频信号注入法常用在直流系统的故障检测中[1]，但环网支路中谐波环流占比较大，通常大于用于检测故障的低频信号电流，这使得检测结果的准确性受到了极大影响。

分形理论[2-3]在处理复杂、零碎问题等方面优势显著，可以从复杂的现象中找出事物的某种规律与联系，而分形维数[4-6]是描述这种规律或特征的一个有效手段。

本研究基于分形理论，利用低频信号注入法，并根据小波变换提取信息并计算分形盒维数，分析分形维数随支路绝缘情况的变化趋势，进而判断出直流系统环网接地故障时支路的绝缘情况。

1 分形理论介绍

1.1 分形的定义

在传统欧式空间中，常常使用一维空间表示线，二维空间表示平面，三维空间表示体，由此也可以引出高维空间。但应注意到，这类空间的维数通常是整数型的，而分形的维数却与传统表示不同，它的维数往往是分数。美国学者曼德勃罗(B.B.Mandelbrot)在1973年首次提出了分形的概念，他把分形定义为部分以某种形式与整体相似。

然而人们在实际的应用中发现这个定义很难包括分形丰富的内容，因此判断一个物体是否为分形时，还要看其是否具备自相似性以及标度不变性。

自相似性指的是系统在不同时间与空间尺度观测到的结构与过程是类似的，也可以指系统或结构在局部上与整体之间的相似，在一些系统的整体与部分之间也会存在自相似性。标度不变性是指在分形物体任选一局部区域，放大后的局部图形依然具有原图的形态特征。下文利用经典的科赫雪花曲线对分形的性质进行解释，如图1所示，科赫雪花曲线在任意大小尺寸下，其局部与全局的形状都是相似的。而且对于任意一个区域进行放大，可以发现放大后的形状与细节均与整体部分相同，无论放大多少次，其形态特征依旧会和整体特征相同，即尺度不变性。

图1 科赫雪花曲线

在实际中，分形物体往往在一定范围内才具有标度不变性。通常把这个空间称为该分形的无标度空间，也就是说只有对无标度空间的系统才能使用分形。

1.2 小波分形技术

分形的自相似特征可以看作尺度从大到小的变换，尺度越小观察到的细节越丰富。因此，对复杂形态的分形分析，实质上就是一种多分辨分析。改变小波变换的尺度因子可以实现小波函数的伸展和收缩，以达到不同尺度下对目标的分析。根据以上分析，分形理论和小波分析在自相似的本质上和认识事物由粗到细的过程是一致的，在这种思想的启发下，有了小波分形技术的提出。

小波分形技术的基本思想是通过小波分解后不同尺度上信号盒维数的大小及其变化，以此分析信号在不同频段内的不规则度和复杂度，刻画信号的非平稳性。

2 环网支路接地故障检测方法

图2展现了本研究检测接地故障的思路流程。当检测元件检测到线路出现异常数值时，由信号源发出低频信号，这里选用了峰值为30 V，频率为20 Hz的正弦电压信号。然后利用传感器对线路的信息进行采集，采集得到的信息进行下一步处理，首先进行滤波，滤除高频信号的干扰，然后对剩余的信号进行小波变换，并计算分形盒维数，分析盒维数与接地电阻之间的关系，从而根据盒维数的大小判断接地情况。

图2 接地故障检测方法

在信号提取环节主要使用了小波变换。傅里叶变换是把信号的统计变换到了频率的领域，适合用于宏观特征分析中。而小波变换主要利用小波函数将不同成分的信号分离出来，它的主要思想是将不同成分的信号区别并进行分析，所以小波变换更适合侦测信号特征，适合复杂信号的分层分析。

在环网支路中，接地电流信号中低频成分占比较大，由此可以实现对接地电流信号和无接地电流信号的鉴别，可以对环网支路电流进行小波的多分辨率分析，并提取环网支路电流低频段成分的特点。

根据采样定理，1 000 Hz的离散采样信号所能反映的最高频率为500 Hz。信号经两次多分辨率分解后得到的2尺度空间概貌系数反映了0～125 Hz的信号分量。计算反映信号概貌系数的分形盒维数，便可得到该信号低频分量的分形特点。

离散信号盒维数计算过程如下，设离散信号x(j)属于空间R2，将空间划分成一个个小网格；若NΔ是边长为Δ的正方形小网格与离散信号相交的网格个数，则离散信号x(j)盒维数可以定义为：

(1)

离散信号x(j)的最高分辨率由采样频率决定，由于信号是离散的，所以上式的极限无法按Δ→0求出，因此采用网格逐步放大(即kΔ，k∈Z*)的方式来计算与信号曲线相交的网格数NkΔ。

本研究中采用了矩形小网格来进行计算，矩形网格宽度与采样时间(Δt)相等，纵向高度为ΔA，则矩形网格可表示为kΔt×kΔA。

(1)确定k值。因为采样信号的间隔为Δt，相邻数据之间用直线相连，所以k取小于1的值将没有意义。假定信号的周期为T，则在一个周期内的数据点有([T/Δt]+1)个([ ]表示取整)，当kΔt大于T/2，作为正负交替的信号其周期性将不明显，所以k的上限为[T/2Δt]+1，综上：

1≤k≤[T/2Δt]+1

(2)

(2) 确定矩形网络高度ΔA。ΔA应能体现振幅尺度的特征，它既不能小于分析信号任意相邻数据点的最小差值ΔAmin，也不能大于信号的峰值Amax，因此在本文中设定：

(3)

(3)计算与曲线相交的盒数量。设矩形网格为kΔt×kΔA，离散的信号序列为s[n﹒Δt]，n=1,2,3,…,N。则整个信号曲线可分为M=[(N-1)/k]个等间距区间；在(N-1)/k的余数非零时，还将有(N-Mk+1)个数据s[m﹒Δt]，m=Mk,Mk+1,…,N组成的窄条格，计算该窄条格下与曲线相交的网格数。改变k值并计算与信号曲线相交的矩形网格个数，然后利用得到的(k2-k1+1)组数据估计线性回归方程的回归系数D，即得到信号曲线的分形维数。

最后分析环网电流的分形盒维数随接地电阻改变的变化趋势，实现环网支路接地故障的诊断。

3 仿真及实验验证

在直流电网环网支路模型中取一条支路对无接地和接地两种情况下的电流信号进行分析(见图3)。

图3 环网支路模型

设负载为300 Ω的环网支路(支路1)在无接地情况下，仅有10 μF的对地电容，电流互感器测得支路电流为i1；支路在接地电阻为100 Ω、对地电容为10 μF的情况下测得的支路电流为i2。

对电流i1，i2分别进行多分辨率分析，得到底层空间的概貌系数。注入的低频信号为20 Hz，它会在有接地电阻的环网支路明显地体现出来。进一步来说，环网接地支路电流i2在0～125 Hz频段内低频注入分量占主要成分；而环网无接地支路n的电流在0～125 Hz频段内除了低频注入分量，由于环流而产生的谐波成分也比较明显。

接下来计算环网支路电流的矩形盒维数。电流信号的采样频率为1 kHz，底层概貌系数的采样频率为1 000/22=250 Hz，电流信号的主频率为20 Hz，由公式(1)得到无标度区间为1≤k≤6，体现信号振幅的矩形网格纵向最小间隔ΔA为：

进一步计算可以得到环网接地支路电流i2的底层概貌系数曲线的盒维数为：

Di2=1.1501

改变k的取值，计算与曲线相交的网格数N，得到k与N的双对数曲线(见图 4)。

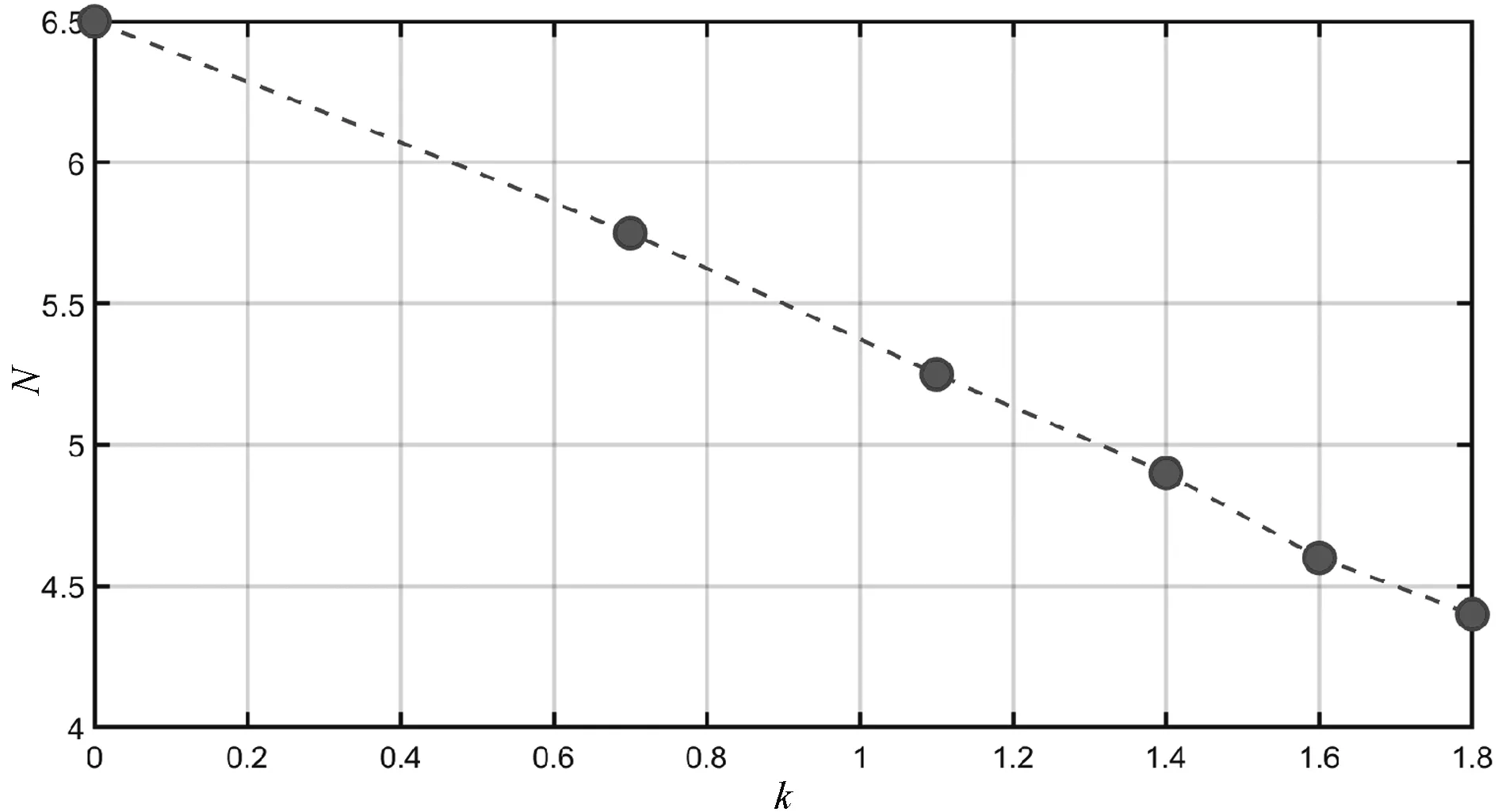
图4 环网接地支路电流i2的k与N双对数曲线

改变环网支路的接地电阻值，计算不同阻值下的盒维数，计算结果如表1所示。

表1 支路1在不同阻值下的盒维数

结果显示，随着接地电阻的增大，电流低频段分量曲线的分形盒维数也在逐渐增大。

在实际应用中，可以根据不同的环网支路及其对地电容情况，计算接地电阻为经验值20 kΩ时的支路低频段分形盒维数，以此作为检测判断标准。通过实时检测并计算环网支路的低频段分形盒维数，对照各自支路的接地盒维数标准，就可以实现环网支路接地状况的实时判断。

4 结语

本研究基于分形理论，利用低频信号注入法、小波变换等方法，对得到的信号的分形盒维数进行了计算，得到了分形盒维数与接地故障之间的联系。在实际应用中，可以利用本文提出的方法，计算各环网支路的接地盒维数标准，对照此标准，就可以实现环网支路接地状况的实时判断。