空间等离子体中的动理学平衡态结构模型

李京寰，杨 帆，周煦之

北京大学地球与空间科学学院，北京 100871

0 引言

在复杂的空间等离子体环境中，一系列电磁结构可通过波动、湍流以及不稳定性等非线性能量串级过程产生，其中包括电流片（current sheet，参考Yuan et al.,2020）、磁洞（magnetic hole 或magnetic cavity,magnetic dip，参考Haynes et al.,2015; Huang et al.,2017; Yao et al.,2020a）、磁峰（magnetic peak，参考Burlaga et al.,2006; Yao et al.,2018a）和磁通量绳（magnetic flux rope，参考Sun et al.,2019; Russell and Qi,2020）等.这些结构广泛分布于日地空间中.以磁洞为例，人们已陆续通过实地卫星观测，在太阳风（Winterhalter et al.,1994）、日球层鞘（Burlaga et al.,2006）、地球磁鞘（Tsurutani et al.,2011）、磁尾（Ge et al.,2011）、行星磁鞘（Cattaneo et al.,1998）和彗尾（Plaschke et al.,2018）中观测到了磁洞的存在.它们的时空尺度可以从磁流体动力学尺度一直跨越到离子甚至电子动理学尺度.因此，它们通常被认为可在能量串级、转化以及耗散中扮演重要的角色.

随着观测手段的进步，人们对空间电磁结构中的电磁场以及粒子分布有了愈加清晰的认知.尤其在MMS（Magnetospheric Multiscale Mission）卫星升空后，其粒子数据拥有的极高时空分辨率使得我们可以对小至动理学尺度的电磁结构进行观测和分析.人们发现，无论磁洞（Gershman et al.,2016;Huang et al.,2017; Liu et al.,2019a）、磁峰（Yao et al.,2018a）还是磁通量绳（Yao et al.,2020b）等不同结构，其大小均可能小至动理学尺度.然而，即使多颗卫星的同时观测给出了丰富的电磁场和粒子信息，人们仍难以完整地描述一个三维的结构，更无法对其物理本质进行更为深入的理解.因此，人们还需要发展理论模型，或利用数值模拟方法对这些电磁结构进行分析.

近年来，一种用于描述空间电磁结构的常用方法是构建动理学平衡态模型，随后结合卫星观测作为辅助，对模型进行验证以确保其可靠性.动理学平衡态模型本质上是动理学方程（例如无碰撞情况下的Vlasov-Maxwell 方程）的定常解，其电磁场及带电粒子分布均不随时间变化，可用于描述处于平衡状态下的电磁结构.动理学平衡态模型的构建不仅可以帮助我们理解其物理本质，还可以为数值模拟工作提供初始条件，用以分析这些结构的不稳定性及演化特征等.在这些模型中，一个应用最为广泛的例子是著名的Harris 电流片（Harris,1962）.该模型通过在直角坐标系下求解Vlasov-Maxwell方程组，得到自洽的电磁场空间分布以及粒子在六维相空间的分布函数.随后，人们陆续提出了一系列用于描述电流片的平衡态模型（Lembege and Pellat,1982; Yoon and Lui,2004; Sitnov et al.,2006）.类似的方法也被用于构建其他结构（如磁洞和磁通量管等）的动理学平衡态模型（Shustov et al.,2016; Li et al.,2020; Li et al.,2021a; Yang et al.,2022）.这些模型往往可以直接与卫星观测进行比较，其相似的结果也很大程度上验证了模型的可靠性，并证实了平衡态电磁结构在空间中的普遍性.同时，这些平衡态模型也可作为数值模拟的初始条件，用于帮助理解空间电磁结构的演化过程（Li et al.,2021b）.本文将简要回顾人们近年来在动理学平衡态模型的构建和应用中取得的进展.

1 电流片模型

电流片是日地空间中广泛存在的电流薄层结构，其两侧方向的磁场显著不同，并常常呈现相反的方向.电流片中的不稳定性过程与磁场重联的发生息息相关，从而导致了空间中的众多爆发过程，如磁层的亚暴、太阳的日冕物质抛射以及耀斑等.在大多数时候，电流片可被视为处于稳态之中，因此平衡态电流片的建模工作对于人们理解其磁力线构型以及带电粒子的运动十分重要.通过在直角坐标系下求解Vlasov-Maxwell 方程，Harris（1962）提出了一维的稳态电流片动理学解析模型，即一个电流片的自洽平衡解.这一模型的出发方程如下：

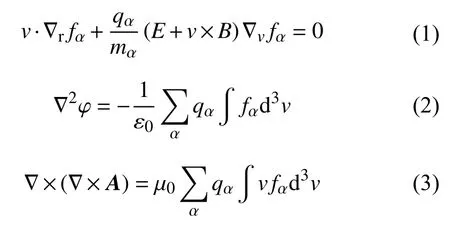
式中，fα代表了等离子体中不同成分的分布函数（α=e,i 分别代表了电子和质子），E、B、A与 φ则分别代表电场、磁场、磁矢势与电势.在这一动理学框架下，如果fα可以写为粒子运动不变量的函数，则平衡态Vlasov 方程（1）将被自动满足.在Harris（1962）中，作者假设物理量仅依赖于x坐标.由于粒子的哈密顿量：

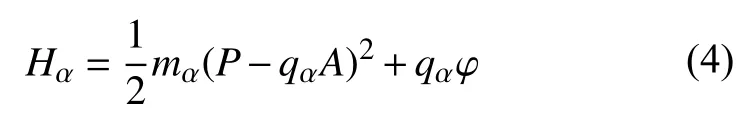
不依赖于y坐标，所以粒子沿着y方向的广义动量保持守恒：

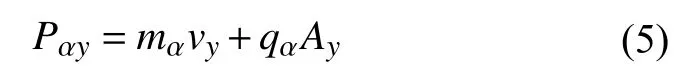
因此，电子与离子的分布函数可以依靠（4）与（5）式中的守恒量来构造：

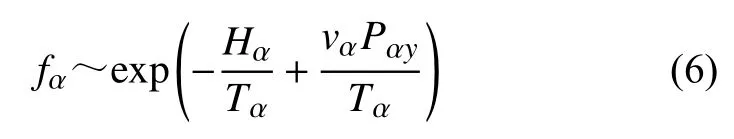
这一分布函数形式为漂移麦氏分布，其中ve、vi分别代表了电子和离子的平均速度，Te与Ti则表示电子和离子温度.将分布函数求矩并代入方程（2）与（3），可以得到两个关于 φ 与Ay的方程.在Harris（1962）中，作者假设平均速度满足ve/Te=−vi/Ti，因此电势方程满足 φ(x)=0，即电场恒为0.随后，对方程求解可获得Ay随x的函数，对其进一步求旋度可以得到磁场Bz=B0tanh(x/L)（图1），其中B0为最大的磁场强度，而L则代表了电流片特征宽度.将磁场分布代入方程（6）即得到粒子的分布函数，对其求矩后则可获得粒子数密度（图1）、平均速度以及压强的一维分布.至此，一个自洽的电流片模型被完整地构造了出来.该模型已成为描述电流片的一个经典模型，被广泛地应用于日地空间物理的研究中.

图1 Harris 电流片模型中的磁场以及数密度的分布（修改自Harris,1962）Fig.1 The magnetic field and number density profiles in the Harris model (modified from Harris,1962)

值得注意的是，Harris（1962）模型只是Vlasov-Maxwell 方程组在直角坐标系下的一个特殊的平衡解.人们可以将方程（6）替换为另一种形式的粒子分布函数，构建各种不同的模型以描述定常态的等离子体电流片.例如，Yoon 和Lui（2004）在（6）式的基础上叠加了一个与空间位置无关的麦克斯韦分布函数，从而使粒子数密度在远离电流片中心的位置不再趋近于零，并允许空间电场的存在，因此与观测更为接近.Sitnov 等（2006）则在（6）式的基础上引入了一个新的不变量，即在电流片中近似成立的绝热不变量Iz（Sonnerup,1971）.这一模型可呈现更为复杂的电磁场形态（如电流的分岔型或镶嵌型结构）和粒子的各向异性分布，从而获得与卫星观测更为接近的结果（Zhou et al.,2009）.

2 磁洞模型

磁洞是局部磁场强度下降，但粒子密度与温度上升，从而使得整体压强仍近似保持平衡的结构.磁洞在空间中的分布极为广泛，并且其尺度可以跨越多个量级，从电子离子的动理学尺度一直到磁流体尺度.MMS 卫星的成功发射为人们提供了高时间以及空间分辨率的实测数据，这也使得人们对动理学尺度的磁洞及其粒子分布的认识有了长足的进步.图2 左侧给出了MMS 卫星在地球磁鞘中对于一个嵌套型磁洞（即在离子回旋尺度的磁洞中心嵌着另一个电子回旋尺度的磁洞）的电磁场及粒子分布的观测（Yao et al.,2017）.根据这一事件的卫星数据，Liu 等（2019a）提出该磁洞在电子尺度下拥有接近圆形的横截面并近似轴对称，其中心处磁场强度的下降则源于磁洞中的环向电流.这些性质与Haynes 等（2015）在PIC 模拟中再现的电子涡旋结构具有高度的相似性.

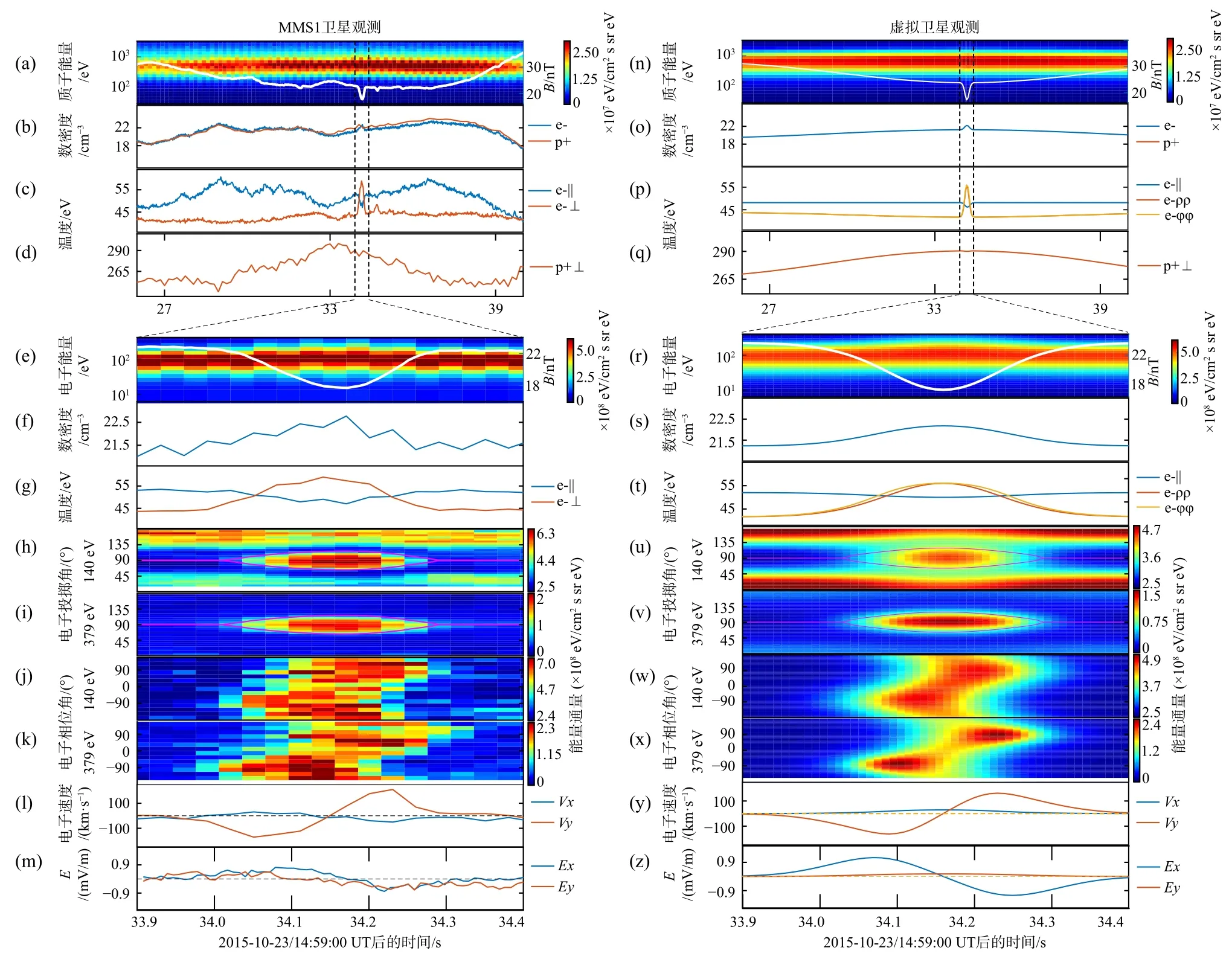
图2 MMS1 卫星嵌套磁洞的观测与虚拟卫星经过平衡态模型之间的对比（修改自Li et al.,2020）.（a）磁场强度以及质子能谱；（b～d）粒子数密度，电子平行与垂直温度，离子垂直温度；（e）磁场强度以及电子能谱；（f～g）电子数密度与温度；（h～i）140 eV 与379 eV 电子投掷角分布；（j～k）140 eV 与379 eV 电子相位角分布；（l）磁洞参考系下的电子速度；（m）磁洞参考系下的电场；（n～z）与图（a～m）格式相同Fig.2 Comparison between the MMS1 observations of nested magnetic cavities and the virtual spacecraft observations across the equilibrium model (modified from Li et al.,2020).(a) Magnetic field strength and the proton energy spectrogram;(b～d)Number density,electron parallel and perpendicular temperatures,and proton perpendicular temperature;(e) Magnetic field strength and electron energy spectrogram;(f～g) Electron number density and temperature;(h～i) Electron pitch angle distributions in the 140 eV and 379 eV energy channels;(j～k) Electron gyro-phase distributions in the 140 eV and 379 eV energy channels;(l-m) Electron bulk velocity and electric field in the rest frame of magnetic cavity.Panels (n～z) are in the same format as in panels (a～m)

图2 左侧的上下两部分分别展示了MMS1 卫星对离子与电子尺度磁洞的观测.离子尺度磁洞（图2a～2d，半径约为500 km）的主要特征包括磁场强度的下降、离子数密度与离子垂直温度的升高.图2e～2m 则展示了放大后的电子尺度磁洞（半径约为10 km）在等离子体静止参考系下的观测（该事件中磁场方向几乎保持不变，用z轴来表示，x轴反向于背景等离子体流的方向）.可以看出，磁洞中磁场强度的快速下降伴随着电子数密度与电子垂直温度的升高.图2h～2k 展示了电子在各能档的投掷角分布以及投掷角90°电子的相位角分布.显然，电子集中于90°投掷角附近，即被束缚于垂直磁场的平面内.电子在相位角分布上存在着明显的各向异性，这一特性在等离子体速度vy分量（图2l）上也被表现为明显的双峰特征，对应于环向电流.图2m 中展示了双峰特征的电场Ex分量（已通过洛伦兹变换），证实了磁洞中存在着径向电场.

仅仅通过观测本身仍然很难判断磁洞的电磁场三维结构以及粒子的全空间分布.与此同时，人们也很难单纯依靠观测理解以下一系列问题：磁洞能否稳定存在？不同尺度的磁洞是如何相互嵌套的？径向电场是如何形成的？磁洞是如何演化的？因此，人们需要通过构建自洽模型，试图从整体上了解一个结构，并通过模拟来更加深刻的理解结构演化中的动理学过程.为了构建一个动理学平衡态的磁洞模型，人们可以利用与Harris（1962）类似的方法求解Vlasov-Maxwell 方程（Shustov et al.,2016; Li et al.,2020）.鉴于磁洞的形态与电流片不同，这一构建过程使用了柱坐标系（ρ,φ,z）以取代电流片模型中的直角坐标系.

假设磁矢势只有环向分量，表示为A=A(ρ)eφ，那么磁场的方向将沿着z轴方向.同时假设静电势φ(ρ)只依赖于 ρ坐标，那么模型中将会只存在径向的电场，且整个电磁场结构是关于 φ对称的.在Shustov 等（2016）模型中，粒子分布可被表达为以下两个运动不变量的函数，即：

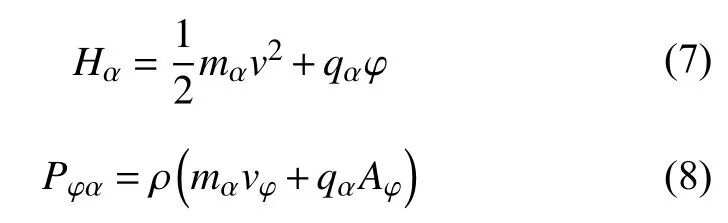
即哈密顿量以及粒子在φ 方向上的广义角动量.鉴于电子尺度磁洞的特征半径远大于热电子的回旋半径，在Li 等（2020）模型中，电子的磁矩 µe被视为另一个运动不变量，即：

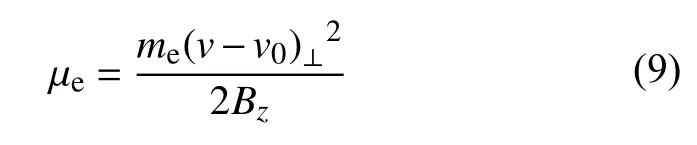
式中，v0代表了回旋中心的漂移速度.随后，电子以及质子的分布函数被表示为：

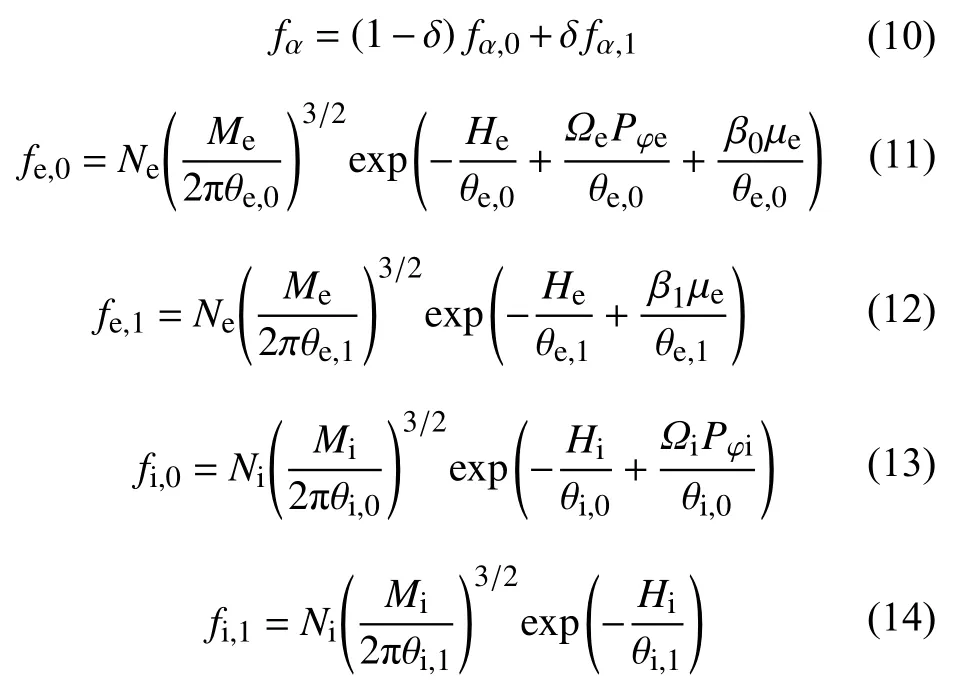
式中，下标为0 的各项中包含Pφ，其固定的系数Ωα代表了粒子绕着轴向转动的平均角速度，而电子与离子不同的平均角速度则代表了不同尺度磁洞的嵌套：在电子尺度内，电流主要由电子的运动提供，而在离子尺度下，电流则主要由离子携带.在磁洞内部，粒子的分布特征主要由以上各项决定.值得注意的是，这部分粒子的平均速度随着距离线性增长，数密度则是指数下降，这显然不符合实际.因此，在分布函数上还需要一个不携带电流的背景分布（用下标1 表示）.这些粒子在远距离处占据主导地位，从而使电流强度随中心距离逐渐降低至零，磁场强度得以收敛在一个定值.可以想象，如果分布函数中只有前两个不变量（Shustov et al.,2016），那么粒子将呈现麦氏分布或者漂移麦氏分布，而粒子的温度则是各向同性的，与电子集中于90°投掷角的观测特征（见图2h～2i）不一致.在Li 等（2020）中，电子温度的各向异性正源于磁矩不变量的引入.在这一分布函数中，θ表征了不同粒子不同成分的平行温度，而常数 β决定了平行与垂直温度之间的比值：当 β>0或者 β<0时，垂直温度将会分别低于或高于平行温度.

将以上分布函数求矩并代入Maxwell 方程组中[在实际操作中，泊松方程（2）可被准中性条件代替]，可得：

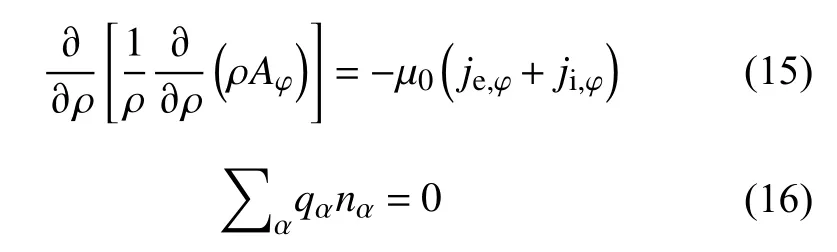
给定合适的边界条件（磁洞模型中心处的参数），通过数值求解方程（15）与（16）即可得到电磁场的分布.将其代入方程（10）中，可得电子和质子在六维相空间的分布函数，进而求矩得到粒子数密度、速度以及温度的分布特征.

这一模型可直接与卫星观测进行比较.对于图2中展现的事件而言，由于MMS1 卫星的运动轨迹极为接近磁洞中心（Liu et al.,2019a），其在中心处的观测数据可被用于选定模型参数，进而重构出磁洞中的电磁及粒子分布函数.令虚拟卫星穿越这一磁洞模型，其结果（见图2 的右侧）很好地重现了左侧MMS1 的真实观测.在Li 等（2020）中，作者将MMS3 和MMS4 卫星的观测结果也与模型的预测进行了对比，发现它们之间同样拥有很好的一一对应关系，这也进一步验证了该模型的可靠性.鉴于多颗卫星相继观测到这一小尺度的结构，该平衡态模型与观测的高度相似性也支持了该小尺度结构可以稳定存在于空间当中的论断.

在以上模型中，由于A=A(ρ)eφ的设定，磁场仅存在轴向分量.但实际观测中还存在着另一类磁洞，其磁场还存在着环向分量.鉴于这类磁洞中的磁力线呈现出扭转的形态，它们被称为螺旋型磁洞（Li et al.,2021a）.显然在这样的结构当中，电流除了包含以上模型中的环向分量之外，也必须存在有轴向分量.图3 左侧展示了MMS 卫星观测到的螺旋型磁洞（等离子体静止参考系，LMN坐标系，其中L轴方向平行于背景磁场）.可以看出，这一磁洞除了展示出与前述磁洞的基本特征（例如轴向磁场强度的下降、密度与垂直温度的上升以及环向电流的出现，见图3a～3d）之外，还有较强的平行电流（图3d）以及与之对应的环向磁场（图3f）.

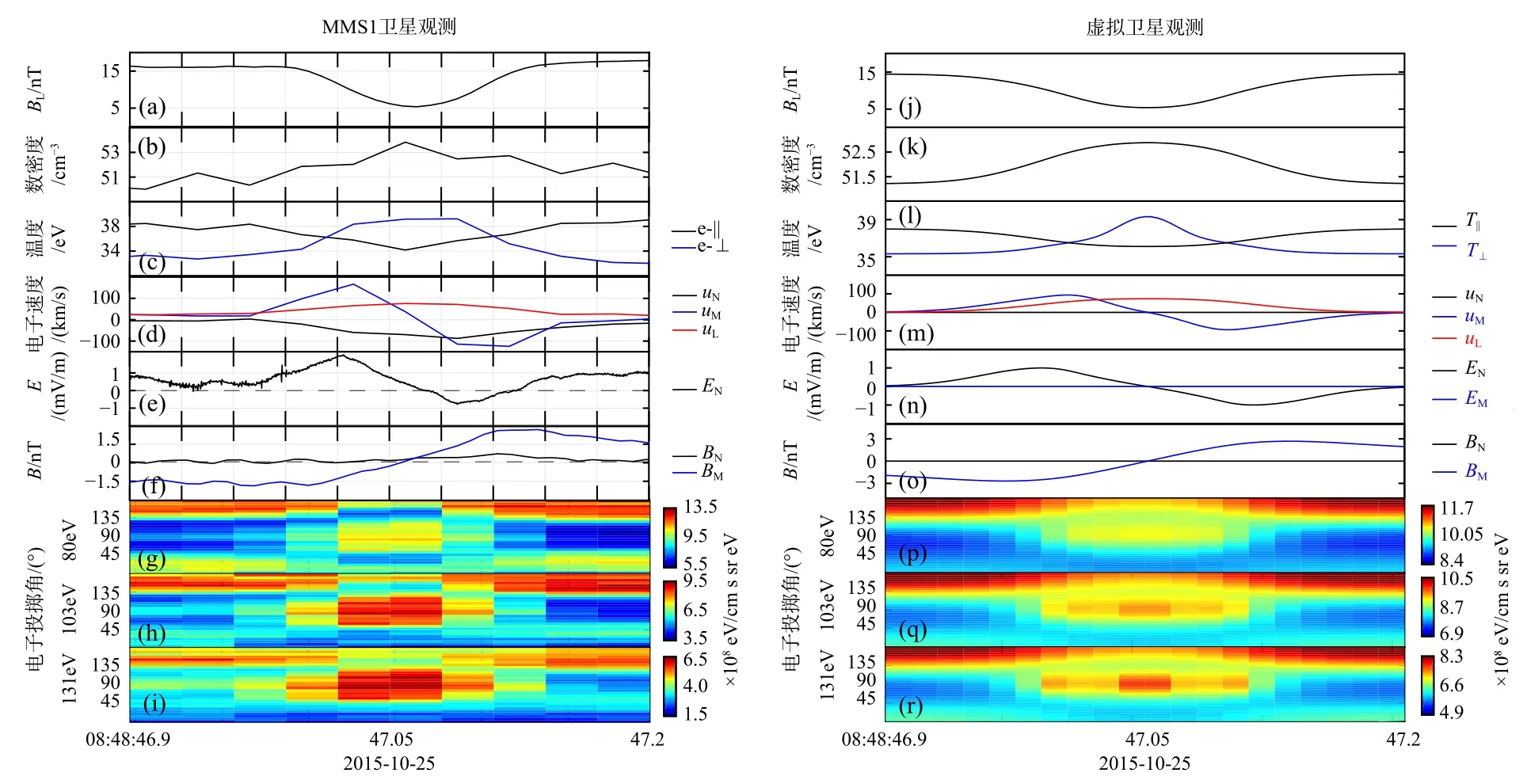
图3 MMS1 卫星螺旋磁洞的观测与虚拟卫星经过平衡态模型之间的对比（修改自Li et al.,2021a）.(a～c)磁场强度,粒子数密度以及电子平行与垂直温度；（d～e）磁洞参考系下的电子速度与电场（LMN 坐标系）；（f）垂直平面MN 磁场分量；（g～i）80 eV、103 eV 与131 eV 电子投掷角分布；（j～r）与图（a～i）格式相同Fig.3 Comparison between MMS1 observations of helical magnetic cavity and the virtual spacecraft observations across the equilibrium model (modified from Li et al.,2021a).(a～c) Magnetic field strength,number density,and electron parallel and perpendicular temperatures;(d～e) Electron bulk velocity and electric field in the rest frame of magnetic cavity (LMN coordinates);(f) Magnetic field MN components;(g～i) Electron pitch angle distributions in the 80 eV,103 eV and 131 eV energy channels.Panels (j～r) are in the same format as in panels (a～i)

为了构造可以描述螺旋型磁洞的动理学平衡态模型（Li et al.,2021a），人们在不变量（7～9）的基础上引入另一个运动不变量，用于构建电子分布函数.这一不变量为轴向的广义动量，即：

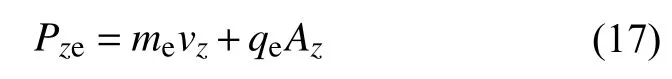
显然，这一不变量的出现可在磁洞中提供轴向电流，其使用条件则是粒子的哈密顿量不依赖于z坐标.因此，磁矢势可表示为A=Aφ(ρ)eφ+Az(ρ)ez，这也意味着模型中存在着与轴向电流自洽的环向磁场Bφ.在这一模型（Li et al.,2021a）中，电子分布函数为：

将其代入方程（3），则会出现两个不同方向分量，其中环向的方程同（15），轴向的方程可写为：

对方程（15，16，19）进行求解，即可得到自洽的螺旋磁洞模型.图3 右侧展示了模型中虚拟卫星穿越该螺旋磁洞的观测结果.可以看出，这一模型描述的电磁场和粒子分布均与观测一致.在这一模型中，磁洞中心磁场强度的下降源于被束缚的粒子在垂直平面的环形运动，而轴向电流则导致了环向磁场的出现，从而使得磁力线被扭曲为螺旋式的结构.

螺旋型磁洞的位形很容易使人们联想到常见的磁通量绳结构.二者在磁场位型上的区别主要在于中心磁场：磁洞的中心磁场较弱，而磁通量绳的中心磁场通常高于远处.因此，人们意识到，对磁洞模型进行适当修改即可用于描述磁通量绳.相关工作将在下一节进行简要介绍.

3 磁通量绳模型

磁通量绳是一种以螺线状磁力线，中心磁场强度上升为特征的空间结构.在卫星数据中，其主要观测特征为一个磁场分量的双极信号和中心磁场强度增强.磁通量绳在磁尾、磁层顶、太阳风等不同区域的观测中广泛存在.在早期空间观测中，磁层顶区域的磁通量绳经常被称为通量传输事件（flux transfer events,FTEs）（Russell and Elphic,1978），并且被广泛认为和磁重联相关（Lee and Fu,1985;Southwood et al.,1988）.最近的数值模拟显示，磁通量绳大至磁流体尺度，小至离子甚至电子尺度都可以存在，并且小尺度（动理学尺度）磁通量绳在磁层的物理过程中扮演了重要的角色（Daughton et al.,2011; Hoilijoki et al.,2019; Lu et al.,2020）.近年来，MMS 卫星提供的高精度观测数据为直接观测小尺度磁通量绳结构带来可能.例如，观测中可以看到互相缠绕的磁通量绳的结构（Qi et al.,2020），从而间接佐证了数值模拟中看到的小尺度磁通量绳相互作用并形成更大尺度的磁通量绳结构的过程.小尺度磁通量绳结构同样也在磁重联的离子扩散区和电子扩散区被观测到（Dong et al.,2020）.磁通量绳在随磁层对流向磁尾移动的过程中，可能会伴随尺度的变化（Hasegawa et al.,2016; Akhavan-Tafti et al.,2019），也可能呈现相对稳态的特征（Eastwood et al.,2012）.在小尺度磁通量绳中，也观测到各种等离子体波动的激发（Wang et al.,2019）以及粒子的加速（Zhong et al.,2020）.

磁通量绳的观测经常显示出无力场结构，即电流与磁力线平行.根据电流是否线性依赖于磁场强度，这类磁通量绳可被分为线性与非线性无力场结构.早期磁通量绳的研究中，人们经常依据磁通量绳的无力场特性构造磁场模型并与观测拟合，例如Lundquist 线性无力场模型（Lundquist,1951）和Gold-Hoyle 非线性无力场模型（Gold and Hoyle,1960）.近期的观测研究表明，许多磁通量绳都显示了非线性的无力场特征（Yang et al.,2014），同时人们也观测到了非无力场的磁通量绳（Bai et al.,2020）.在离子尺度无力场磁通量绳的典型观测中（Eastwood et al.,2016; Yao et al.,2020b），人们发现由电子携带的电流可被嵌套于稳定的离子流中，同时也时常观测到丝状电流和非理想的离子特征.根据Sun 等（2019）的统计结果，具有二维结构的离子尺度磁通量绳更可能具有无力场特征，并且经常可以被具有圆形截面的磁通量绳模型拟合.

尽管观测中小尺度磁通量绳显示出丰富的粒子观测特征，传统的磁通量绳模型仍以磁场模型为主，不能很好地解释动理学尺度的物理过程.其中一种方法是根据EMHD 理论对观测到的磁通量绳结构进行重构（Hasegawa et al.,2021），这种方法已经被广泛用于磁重联中电子扩散区的研究.另外一种方法则是构建动理学平衡解（Allanson et al.,2016;Vinogradov et al.,2016; Ng,2020），并利用卫星观测数据确定模型参数，从而实现重构的目标（Yang et al.,2022）.

图4 展示了MMS 卫星对离子尺度磁通量绳的一个典型观测.这一事件最早由Yao 等（2020b）报道，其磁场信号（图4a、4b）显示出了典型的磁通量绳特征（一个分量呈现双极信号，总磁场强度增强）.这一事件的粒子观测则显示出了等离子体密度（图4c）、速度（图4d、4e）和温度（图4f、4g）在磁通量绳内的变化.此外，电子的投掷角分布在30～66 eV 的能量范围内显示出了在90°附近集中的特征.为了解释这些观测特征，Yang 等（2022）构造了一个自洽的磁通量绳模型.

考虑到磁通量绳的几何形态，磁通量绳的动力学模型构造和螺旋磁洞非常类似，即使用不变量Hα、Pφα、Pzα构造分布函数，同时为了解释电子温度各向异性，在电子分布函数中使用了磁矩 µe.磁通量绳和螺旋磁洞的一个主要区别在于中心磁场是增强的，因此可以用如下的分布函数构造：

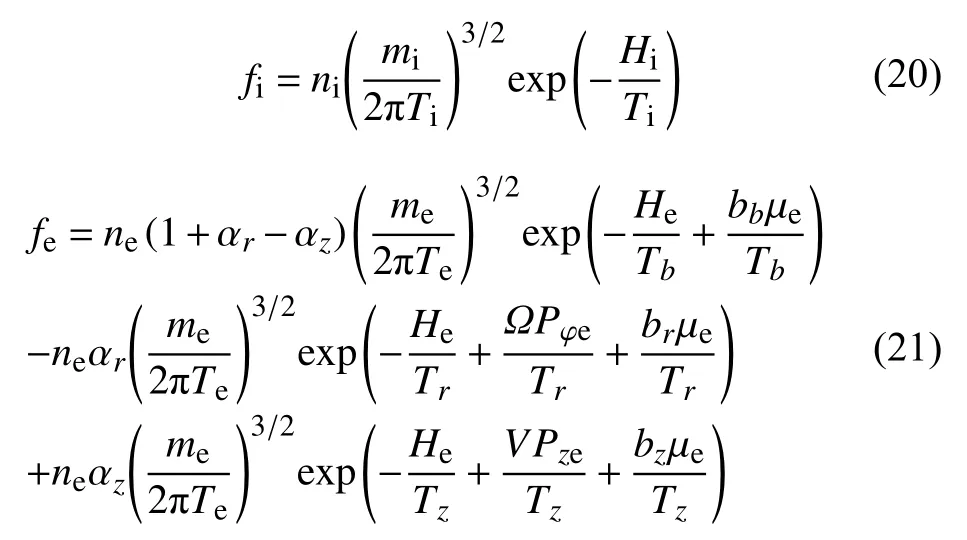
在这一分布函数中，离子的分布函数被设定为麦氏分布，电子被设定为多个类Harris 双麦氏分布的线性组合.这一设定与Vinogradov 等（2016）的磁通量绳模型类似，只是增加了对磁矩不变量的依赖.值得注意的是，为了保证距离磁通量绳足够远处电流为零，（21）式的第二项（环向电流项）系数需要为负，即 αr>0.如果 αr<0，则环向电流项系数为正，模型将会给出类似于螺旋型磁洞的结果.由于当 αr>0时电子分布函数可能出现负值，在模型参数的选取中需要进行额外的限制（例如，Tb>Tr）以避免这一非物理形式的出现.

将分布函数代入式（15）、（16）、（19）求解，可得到自洽的磁通量绳电磁场和分布函数.图4a～4g的虚线展示了这一事件中模型给出的磁场、密度、电子速度、电子温度，它们与卫星观测结果（实线）符合得很好.图4m～4p 展示了模型给出的投掷角分布和观测投掷角分布对比，可以看到，模型同样复现了30～66 eV 能档处90°附近电子通量上升的现象.MMS 星座其他3 颗卫星的观测和模型结果也符合得很好（Yang et al.,2022），证明了这一模型的可靠性，并支持了磁通量管作为一个小尺度平衡态结构，可以稳定存在于空间中的论断.

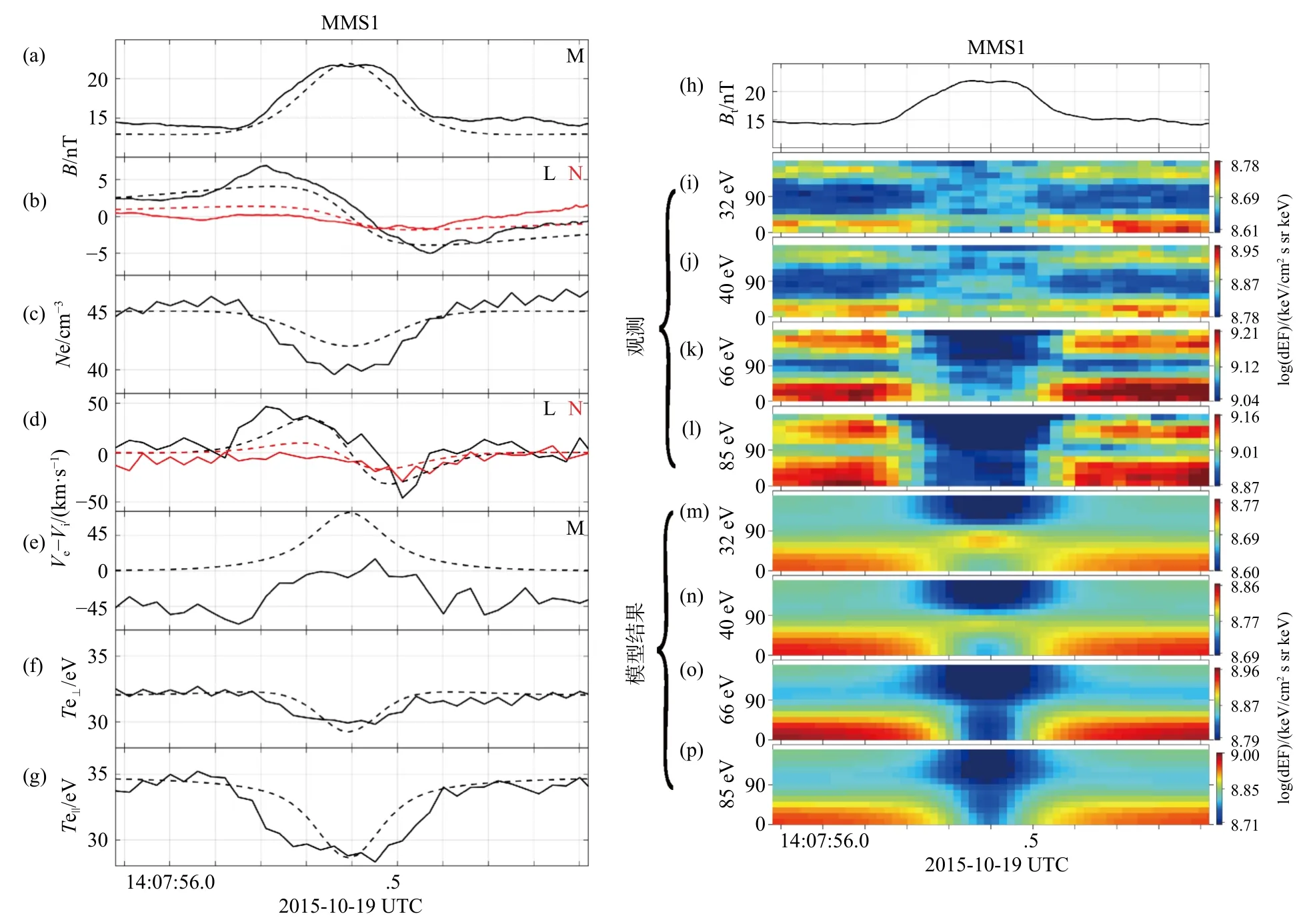
图4 MMS1 卫星对磁通量绳的观测与平衡态模型结果的对比（修改自Yang et al.,2022）.(a～g) 一些观测量的时间序列图.(a～b) 磁场三分量；(c) 电子数密度；(d～e) 电子相对离子速度；(f～g) 电子垂直温度和平行温度；(h) 观测总磁场强度；(i～l) 观测32 eV、40 eV、66 eV、85 eV 投掷角分布；(m～p) 模型对应能量的投掷角分布Fig.4 Comparison between MMS1 observations and model results of flux ropes (modified from Yang et al.,2022).(a～g) Time series plots for some quantities;(a～b) Magnetic components;(c) Electron number density;(d-e) Electron bulk velocity relative to ion;(f～g) Electron perpendicular and parallel temperature;(h) Total magnetic strength;(i～l) Pitch angle distribution at 32 eV,40 eV,66 eV,85 eV given by observations;(m～p) Pitch angle distribution given by model results at the same energy channels

在这个模型中，泊松方程（2）被简化为准中性方程（16）.这一简化成立的前提是，径向电场造成的电荷分离效应相比电子总密度可以忽略不计（δn≪n）.尽管这一条件在绝大多数情况下均成立，人们也同样进行了直接求解泊松方程以构建磁通量绳模型的尝试.Ng（2020）考虑了fe∝exp(−H/T)−形式的分布函数，并假设离子密度为恒定值，通过直接求解（2）式和（3）式获得了自洽解.这种模型充分考虑了电子和离子密度分离的效应，因此对径向电场的估计更加准确.

在Allanson 等（2016）中，作者不仅设定了粒子分布函数，还额外预设了电场和磁场的形式：

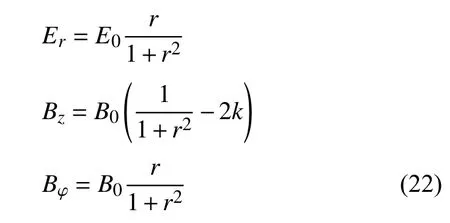
通常而言，这些额外的假设会造成Maxwell 方程超定.但在这里，电磁场特殊的形式使得（2）式和（3）式两边都可化为A(1+r2)Bexp(Cr2)的组合形式，从而将微分方程化为两边系数相等的代数方程，并最终获得一个非准中性的解析特解.应当指出，在Allanson 等（2016）模型中，为了保持电磁场和分布函数的解析性，作者加入了多个模型参数的约束.因此，这一模型的自由度远小于其他磁通量绳的动理学模型（例如Vinogradov et al.,2016; Yang et al.,2022）.这些额外的约束未必具有物理意义：在不满足这些约束时，人们也可以通过数值方法得到磁通量绳的自洽解.

4 动理学平衡态模型的应用

动理学平衡态模型的构建对人们理解空间结构的演化有很大的帮助.例如，模型结果可以作为初始条件代入数值模拟过程，从而协助人们理解这些结构的稳定性和演化过程.由于这些模型中包含了电磁场和粒子的自洽分布，因此人们可以使用动理学方法（如Particle-in-Cell 等）进行数值模拟，也可以基于其中的部分信息，使用相对简单的数值方法（如传统的磁流体动力学模拟或试验粒子模拟）对感兴趣的物理过程进行分析.

这一方法已在电流片微观不稳定性及磁重联的研究被广泛应用.其中，一个著名的例子是美国国家科学基金会（NSF）地球空间环境模型（GEM）项目组织开展的磁重联挑战活动（Birn et al.,2001）.在这一活动中，人们将Harris（1962）电流片模型作为初始条件，利用各种数值模拟程序分析电流片的演化过程，并通过对不同数值模拟结果的对比，试图理解磁重联背后的物理过程.除此之外，也有大量研究基于类似的方法，分析各种电流片平衡态模型在不同条件下的演化过程，并试图用其解释近地空间中发生的一系列物理过程（Pritchett and Buechner,1995; Pritchett and Runov,2017）.鉴于这一方法已历经长期的发展，此处不再详述.

另一方面，由于磁洞或磁通量管的动理学平衡态模型发展较晚，基于这些模型开展的数值模拟工作还十分有限，但仍不乏亮点.Li 等（2021b）基于此前发展的磁洞模型（Li et al.,2020），并利用单粒子模拟程序，试图理解MMS 卫星观测到的“甜甜圈”型电子投掷角分布（Yao et al.,2018b）.图5a展示了MMS 卫星在磁鞘中观测到的一连串磁洞，以及与之对应的两种不同的电子投掷角分布（图5b和图5c）.其中，一种分布更加集中于90°投掷角（见图5h），这种分布与Li 等（2020）平衡态模型特征一致.另一种则呈现“甜甜圈”形态（见图5e）：在磁洞的中心处，投掷角为90°的电子相空间密度低于中等投掷角的电子相空间密度，而在磁洞的边缘处，90°投掷角电子的相空间密度最高.由于这两种分布是交替出现的，作者推测，后者可能源于前者在磁洞演化过程当中的演变，并通过磁洞演化叠加单粒子模拟的方法来对该假设进行验证.

图5j～5m 给出了模拟的初始状态，即基于Li等（2020）模型的平衡态磁洞.此时电子的投掷角分布呈现出集中于90°的特征.鉴于在观测中，人们时常发现磁洞在演化过程中可经历加深与收缩（Ahmadi et al.,2018; Liu et al.,2019b），在这一模拟过程中，Li 等（2021b）在平衡态模型电磁场的基础上叠加了随时空变化的扰动场，用以表征磁洞的演化过程（如图5n 和5o 所示）.随后，作者通过反向追踪电子的轨迹，并基于刘维定理（粒子随体的相空间密度保持不变），得到磁洞演化过程中任意时间与空间位置的投掷角分布（图5p）.模拟结果呈现出了与观测非常相似的“甜甜圈”特征，且该特征随着演化程度的加深愈加显著（由图5n到图5r）.这一结果支持了电子“甜甜圈”分布起源于磁洞收缩和加深的演化过程的假说.基于这一模拟结果，作者还分析了典型电子轨迹与能量变化，讨论了电子Betatron 减速、径向传输和投掷角变化在这一过程中的作用.

图5 MMS1 卫星对一系列磁洞的观测以及虚拟卫星在磁洞演化过程中的观测（修改自Li et al.,2021b）.(a～c) 磁场强度与电子投掷角分布；（d～f）以及（g～i）与图（a～c）栏格式相同；（i～k）平衡态磁洞电磁场分布；（l～m）平衡态磁洞电子投掷角分布；（n～o）磁洞演化过程中扰动磁场与电场；（p～q）磁洞演化过程中电子投掷角分布；（r～u）与图（n～q）栏格式相同Fig.5 MMS1 observations of coherent magnetic cavities and virtual spacecraft observations across the evolving magnetic cavity(modified from Li et al.,2021b).(a～c) Magnetic field strength and electron pitch angle distributions; Panels (d～f) and (g～i)are in the same format as in panels (a～c);(j～k) Electromagnetic fields in the equilibrium magnetic cavity model;(l～m)Electron pitch angle distributions in the equilibrium magnetic cavity model;(n～o) Perturbed electromagnetic fields during the magnetic cavity evolution;(p～q) Electron pitch angle distributions during the magnetic cavity evolution; Panels (r～u) are in the same format as in panels (n～q)

在这一例子中，作者仅使用了单粒子模拟对磁洞演化过程中粒子的响应进行了分析，但并没有考虑粒子对磁洞演化过程的反作用.更为精确的物理描述将有赖于更为自洽的数值模拟方法（如Particlein-Cell 模拟等）.这一模拟的初始条件同样可由动理学平衡态模型给出.

5 讨论与未来展望

本文主要关注空间等离子体环境中的多种多样的电磁结构（如电流片、磁洞和磁通量绳等），并针对这些结构，回顾了动理学平衡态模型的构建方法.这种方法基于统一的物理框架，即通过构建带电粒子随运动不变量的分布函数求解平衡态Vlasov-Maxwell 方程组，自洽的获得结构内部的带电粒子及电磁场分布.随着多卫星、高精度观测数据的逐渐增多，这些理论模型得以被更充分的验证.目前，关于动理学平衡态模型的研究仍在进行之中，其主要发展方向和存在的问题如下：

（1）除电流片外，目前的动理学平衡态模型大多局限于一个空间变量（即一维模型）.而空间观测中许多结构（例如磁镜模结构）无法用单个空间变量的平衡态模型描述.在柱坐标系下，若电磁场和粒子分布函数与r、z两个空间坐标有关时，是否存在平衡解？

（2）长期以来，关于动理学平衡态模型的工作大多偏向于理论，其重点在于分布函数形式的构造及其与电磁场形态之间的关系等.相对而言，这些工作在模型与观测对比方面的处理则通常比较简略.近年来，伴随高精度多点观测数据增多，电磁结构的多卫星观测工作十分丰富.关于如何利用多卫星观测技术进行模型和观测的对比，不同的对比方法的可靠性和不确定度如何，目前尚没有成体系的工作.

（3）尽管人们利用电流片平衡态模型作为初始条件开展了大量数值模拟工作，基于磁洞或磁通量管的相关工作仍然很少.鉴于人们在磁洞与磁通量管的观测中已发现了多种多样的等离子体波动以及丰富的粒子动力学特征，未来的一个重要研究方向将是通过模拟工作重现这些特征，从而协助人们反推这些电磁结构的演化过程，并对波粒相互作用等能量传输过程建立更深刻的理解.