电离层氧离子外流对磁层的影响

陈俊杰，张彬铮，奥利弗·布兰布尔斯

1 香港大学 地球科学系，中国香港 999077

2 达特茅斯学院塞耶工程学院，美国汉诺威 03755

0 引言

1960 年代就有理论提出，极区电离层的离子可以如图1 所示沿着开放磁力线外流（outflow）到磁层 （Axford,1968; Banks and Holzer,1968,1969），这被称为极盖区离子外流（polar cap ion outflow）或极风（polar wind）.在经典理论中，离子外流一般狭义地指来自地球电离层较热的轻离子外流，主要是H+离子、He+离子和电子.在极区顶部电离层，这些轻离子受到向上的压力梯度力超过向下的重力时，它们会沿着磁力线向上输运到磁层，同时由于双极扩散作用会产生双极电场使得电子也跟着离子运动，使得外流物质在宏观上电中性.这种典型的离子外流在卫星结果中很常见（Hoffman and Dodson,1980; Nagai et al.,1984; Chandler et al.,1991; Abe et al.,1993a,1993b,2004; Kitamura et al.,2011）.

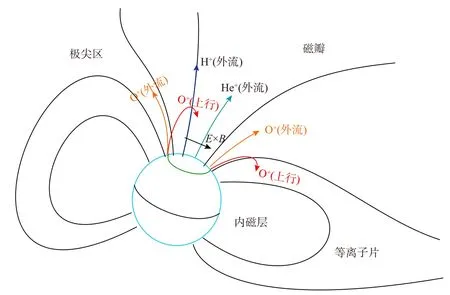
图1 电离层离子上行和外流过程示意图（修改自 Zhang and Brambles,2021）Fig.1 The ionospheric ion upflow and outflow （modified from Zhang and Brambles,2021)

按照经典理论的预测，其他重离子如O+离子基本都被重力束缚在电离层，不易发生外流现象.但不断有卫星结果表明，磁暴期间日侧极尖区或者夜侧极盖区边界（如图1）发现外流的超热O+离子，粒子能量从几十eV 到keV 量级（Shelley et al.,1972; Bouhram et al.,2004b; Lennartsson et al.,2004; Andersson et al.,2005; Peterson et al.,2008）.这种超热O+离子外流被称为非典型极风.这一类离子外流有两种主要物理机制，第一种机制是场向电场引起的离子场向加速，另一种是波粒相互作用驱动的离子横向加速.由于电离层—磁层系统中场向电场一般很弱且机制较简单，因此大多数研究都重点探究离子横向加速机制.当磁层受太阳风影响发生剧烈扰动时，顶部电离层（1 500～3 000 km）等离子体与来自磁层的宽带极低频波相互作用，会在垂直磁场方向回旋共振而加热成为超热离子，并伴随向上的磁镜力，当磁镜力大于重力时就能向上加速发生超热离子外流.该效应一般作用于O+等重离子，这是因为重离子的回旋半径大（Lemaire and Scherer,1978; Cladis,1986;Demars et al.,1996; Ganguli,1996）.由于该过程在顶部电离层以下区域失效，因此要发生超热O+离子外流，O+离子要先从电离层峰高F2层区域上行（upflow）到顶部电离层（见图1），这主要与两个过程相关.一个是磁层强对流时注入的坡印亭通量（Poynting flux）会加热中性粒子，进而通过碰撞加热电离层O+离子；另一个是磁层软电子沉降加热电离层电子，从而增强双极场向电场（Wiltberger,2015）.此外，电离层离子外流会影响磁层的结构、成分和动力学演化过程，本文将以此为主要内容详细展开讨论.

电离层O+离子外流不是一个孤立的物理过程.大部分外流的O+离子群在到达磁层后，可以改变磁层的局部特性，甚至会影响整个磁层系统的动态结构.反过来，这些磁层动态结构的变化会调制注入极区电离层的能量，从而改变顶部电离层O+离子外流相关的驱动过程，形成复杂的非线性反馈.图2 显示了电离层O+离子外流影响太阳风—磁层—电离层—热层耦合系统的可能物理途径.这些途径包括：

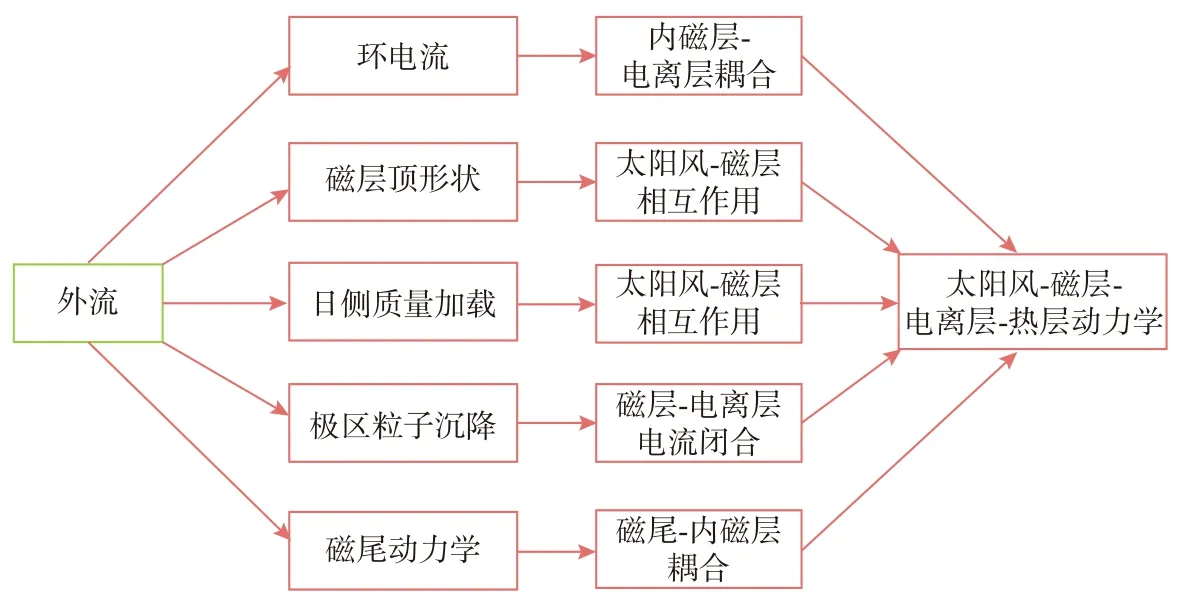
图2 电离层外流影响太阳风—磁层—电离层—热层耦合系统动态结构的示意图（修改自Zhang and Brambles,2021）Fig.2 Pathways of ionospheric outflow on the dynamics of the solar wind-magnetosphere-ionosphere system (modified from Zhang and Brambles,2021)

（1）通过影响日侧磁层质量加载和磁层顶形状来改变太阳风—磁层相互作用；

（2）通过改变磁尾动力学影响磁尾—内磁层耦合；

（3）通过调制环电流和极光粒子沉降来影响磁层—电离层耦合过程.

虽然极盖区H+离子外流在卫星观测中也很常见，但本文我们只关注超热O+离子外流对磁层动力学的作用，这是因为O+离子不仅会通过改变磁重联过程对太阳风—磁层—电离层系统产生更大的影响（如，Brambles et al.,2010），而且会通过与环电流之间的反馈回路，对地球空间系统动力学的产生重要的影响（如，Welling et al.,2015）.由于缺乏卫星观测全球覆盖，全球磁层—电离层耦合模式就成为了研究O+离子外流过程及其相应的空间天气效应的重要工具.因此，我们基于全球磁层模拟做一系列数值实验来探究O+离子外流对磁层的作用.关于O+离子对磁层动力学作用的讨论主要集中在O+离子群的空间分布和磁重联的相应变化上.大多数模拟结果是由观测数据驱动的，直接或间接通过使用卫星测量来验证，要注意的是，简化的理想控制模拟只是提供了对O+离子外流可能影响的理论估计，相关结论仍需要未来的太空任务来进一步验证.

1 极尖区O+离子外流的分布特征及其对磁层的影响

理解极盖区离子外流作用的第一个问题是O+离子到达磁层的什么位置，因为这决定了这些外流O+离子对地球空间环境动力学尤其是对磁层的具体作用.这些O+离子整体上沿磁力线移动，同时伴随垂直磁力线的E×B漂移.因此外流的O+离子的到达磁尾的位置主要由（1）电离层源区位置与（2）场向和横向运动共同决定.如图3 所示，一般场向速度较快（20～100 km/s）的热O+离子外流倾向于落在近重联线（X 线）的尾部并在磁尾耗散掉，这对磁层动态结构的影响较弱.而场向速度较慢（1 km/s量级）的冷O+离子外流主要落在等离子片区域内，这会显著影响磁层动态结构以及重联过程.磁层中O+离子外流位置的空间分布取决于电离层O+离子外流速度的现象被称为“速度过滤效应”.除了极尖区（cusp），源于极盖区极光弧（polar cap arc）的极风中O+离子外流通量也可达到1012m−2s−1量级.而离子外流的分布不仅受外流速率的影响，会受到行星际磁场、太阳天顶角和晨昏不对称性等因素调制，并与其离子、电子温度的大小息息相关（Skjæveland et al.,2014; Maes et al.,2015）.

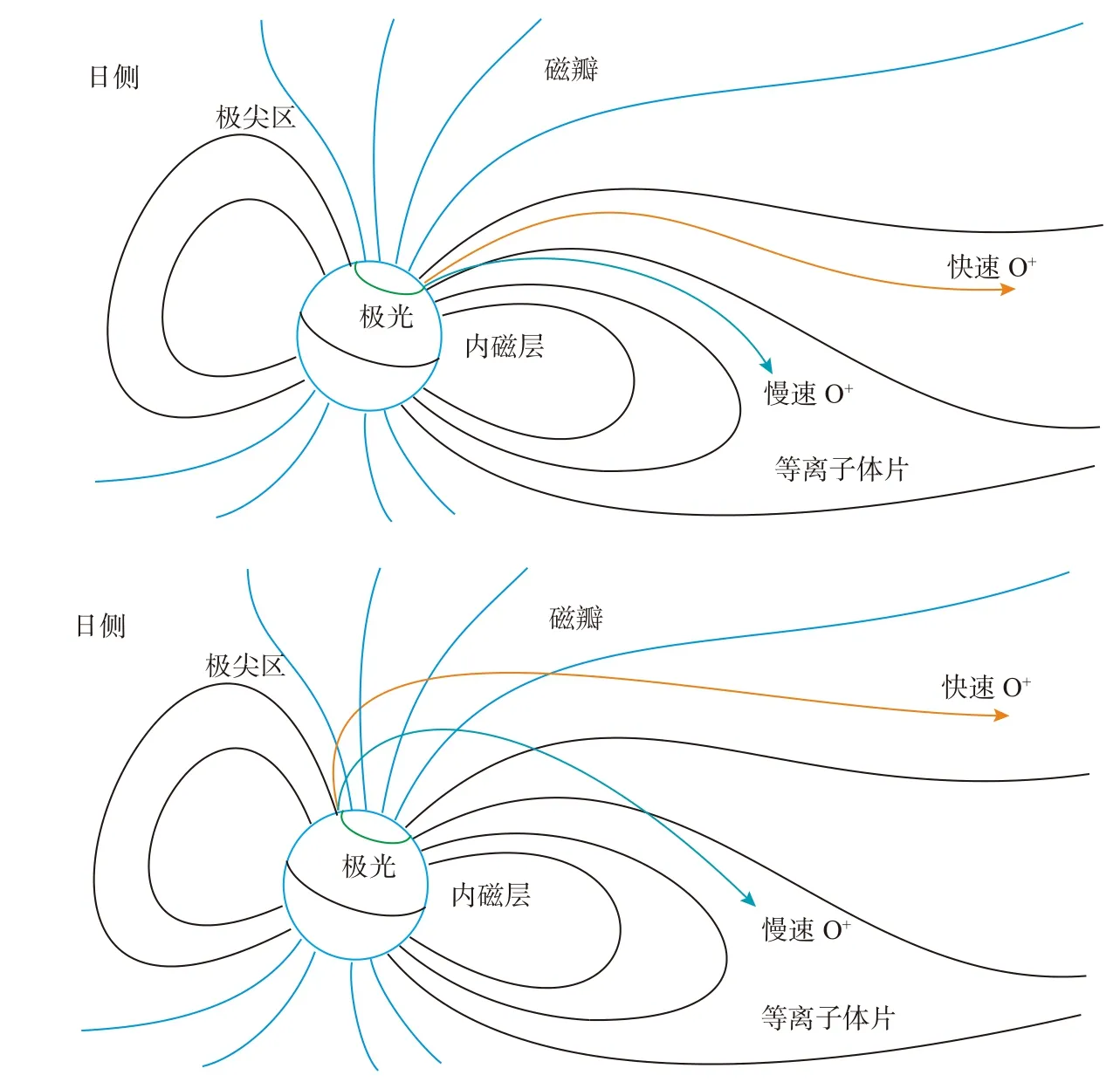
图3 不同速度的O+离子外流过程（修改自Zhang and Brambles,2021）Fig.3 The velocity-dependent landing of O+ ion outflow (modified from Zhang and Brambles,2021)

Brambles 等（2010）首先用全球磁层模拟研究了极尖区O+离子外流的速度过滤效应.他们利用控制模拟实验，探究了2005 年8 月31 日磁暴期间电离层O+离子外流的到达位置和对磁层的影响.该磁暴为中等强度，在与行星际磁云相遇的5 小时内，最小磁暴扰动（disturbance storm time,Dst）指数为−140 nT，行星际磁场（interplanetary magnetic field,IMF）Bz分量为−18 nT.该全球模拟结果来自太阳风—磁层—电离层全球耦合模型Lyon-Fedder-Mobarry（LFM）的多流体扩展版本（Lyon et al.,2004; Brambles et al.,2010）.它在LFM 磁层模型的单流体版本基础上，使用了多离子流体的方法，该方法允许每种离子成分在各自受力平衡下运动.磁暴事件期间观测到的太阳风数密度（NSW）、速度（VSW）和声速（CS）以及IMF 分量（Bx、By、Bz）被用作驱动全球模拟的上游边界条件，其时间变化如图4 所示.

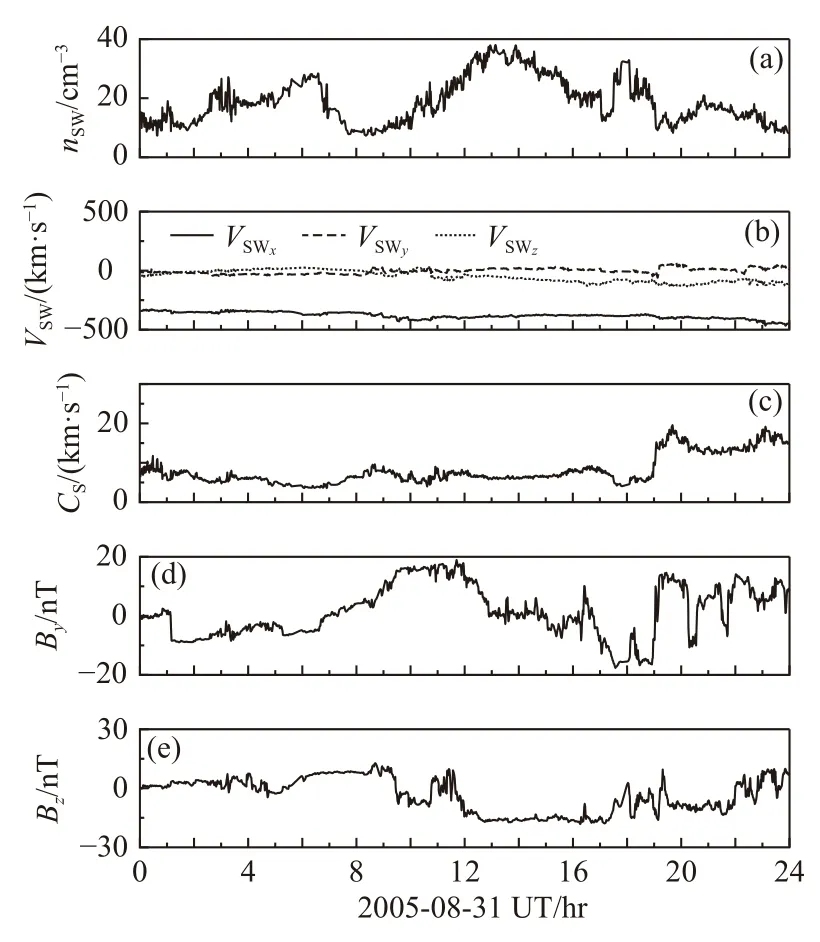
图4 2005 年8 月31 日磁暴的太阳风和行星际磁场条件（修改自Brambles et al.,2010）Fig.4 Solar wind and interplanetary magnetic field for the August 31,2005 storm (modified from Brambles et al.,2010)

为了在全球模拟中加入动态的O+离子外流，基于Strangeway 等（2005）中图5 所示的观测离子外流通量和DC 坡印亭通量的相关性拟合公式，Brambles 等（2010）在模拟的内边界（距离地心2RE处）使用了如下O+离子外流通量经验公式：

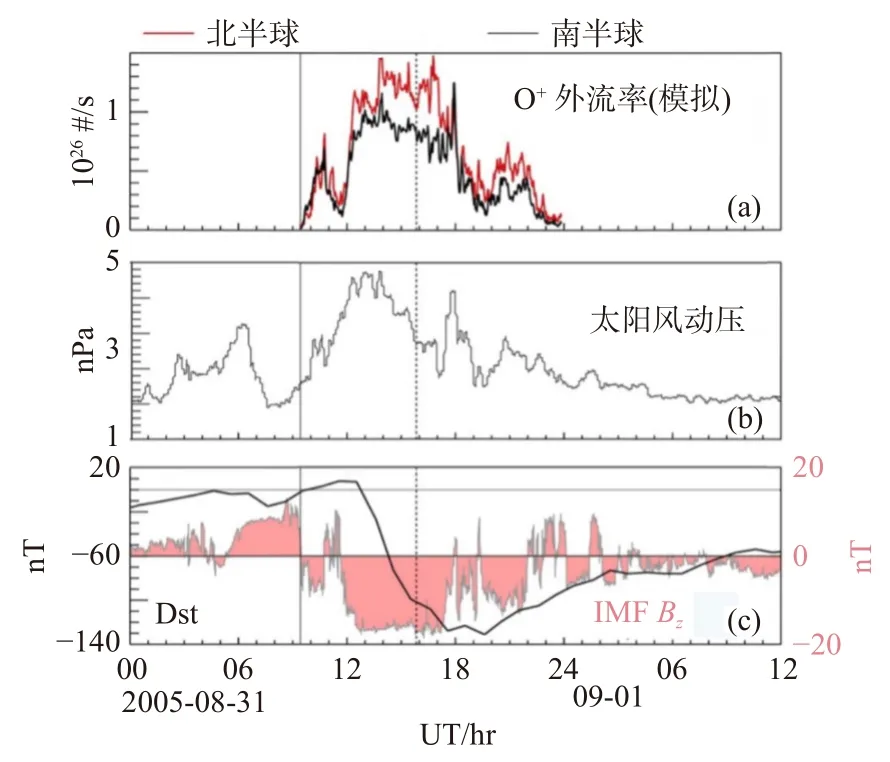
图5 2005 年8 月31 日磁暴特征.（a）模拟的北半球和南半球的电离层O+离子外流率；（b）上游边界的太阳风动压；（c）Dst 指数与作为模式上游边界行星际磁场 Bz（修改自Brambles et al.,2010）Fig.5 August 31,2005 storm characteristics.(a) Simulated O+outflow rate in the northern and southern ionospheres;(b) The solar wind dynamic pressure at upstream boundary,and (c) the IMF Bz at the global model's upstream boundary superimposed on the measured Dst index (modified from Brambles et al.,2010)

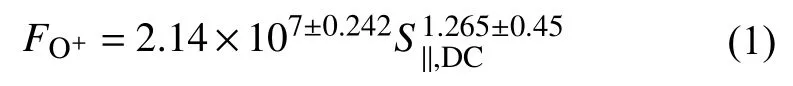
图5 展示了模拟中Case A 北半球和南半球电离层积分O+离子外流率、太阳风动压、Dst 指数和IMFBz.很明显，模拟中半球O+离子外流速率受行星际驱动参数如上游IMFBz和太阳风动压的控制.虽然这里的O+离子外流模型只是一个经验公式，即没有考虑横向加热的物理细节，但模拟结果仍显示了南向 IMF 增强确实增大了流入电离层的DC坡印亭通量，从而导致极尖区电离层O+离子外流通量增强，这一响应与原位探测的结果一致.太阳风动压的增强通过改变磁层—电离层发电机过程来增加日侧DC 坡印廷通量，从而如经验公式（1）所示提高了模拟中O+离子外流率（Newell et al.,2006; Damiano et al.,2010）.在该模拟中，北半球的积分O+离子流出率峰值为1.6×1026#/s−1，映射到电离层100 km 处单位面积外流峰值为1.7×1013#/(m2s).模拟得到的夏季半球的积分外流率高于冬季半球，这与Lennartsson 等（2004）的观测统计一致.模拟中出现南北不对称性是因为控制外流的DC 坡印廷通量在夏季半球比冬季半球要大.观测中电离层焦耳耗散与全球模拟中场向电势差驱动粒子加速下降所消耗的功率接近，因此可以假设模拟内边界的DC 坡印廷通量等于电离层焦耳耗散，因此DC 坡印亭通量可以表征磁层对流注入电离层的能量.

图6a、6b 展示了Case A 和Case B 于15 世界时（UT）在距离地心6RE处模拟的外流通量、电离层电势等值线（白线）和开放/闭合磁力线边界（黑线）.在这两种条件下，O+离子外流主要位于极尖区域附近的对流喉部，大多数磁层DC 波印廷通量在该区域流入电离层，纬度和地方时与Lennartsson 等（2004）的观测结果一致.外流位置也与所谓的极尖区加热壁（polar cusp heating wall）存在相关性（Knudsen et al.,1994），其中引发O+离子外流的横向加热开始于开放/闭合磁力线边界极向1°～2°的位置.

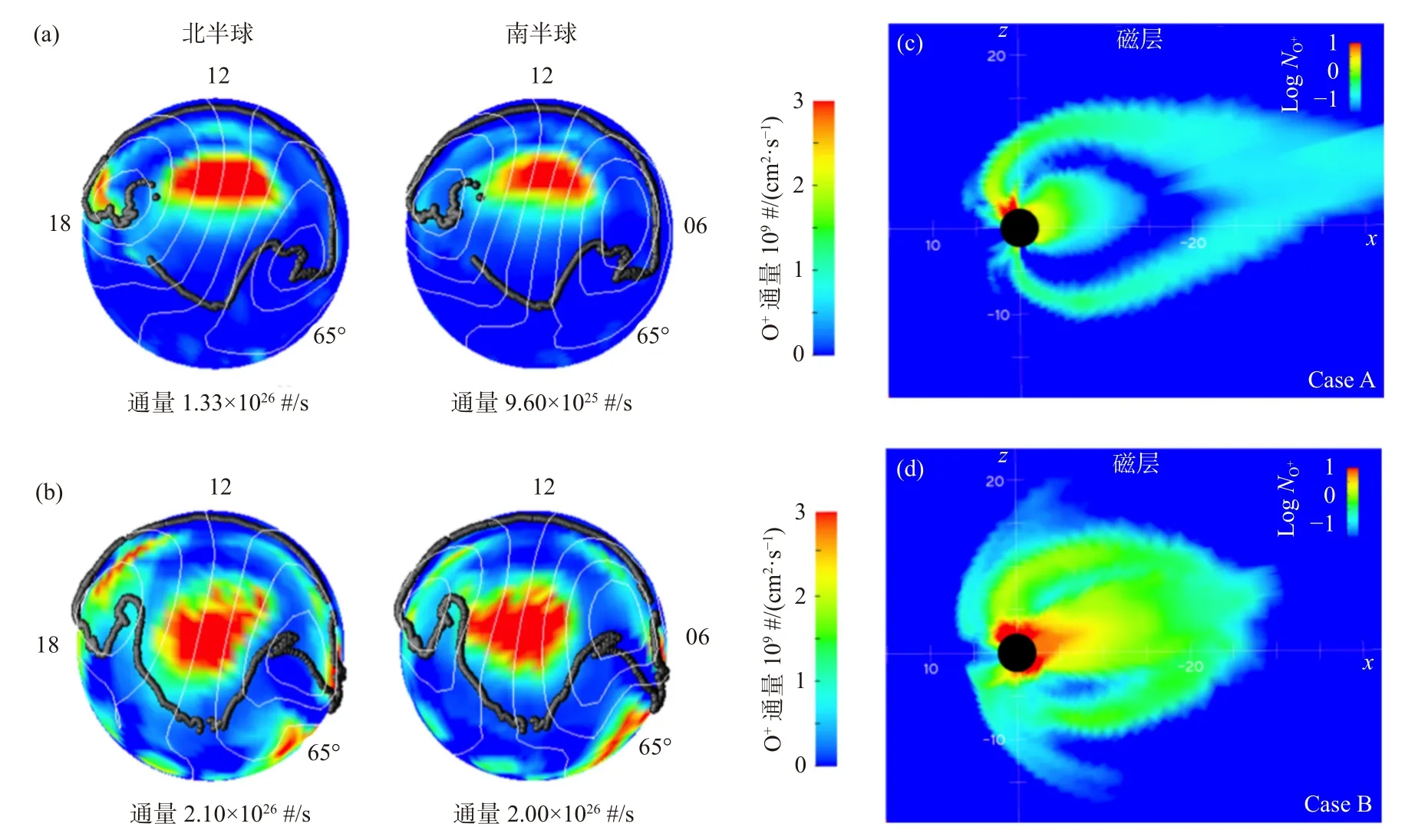
图6 （a）Case A 和（b）Case B 在距离地心6 RE 处的外流通量.在地心太阳磁层坐标中的 x-z 切面（c）Case A 和（d）Case B 的O+离子数密度的对数（修改自Brambles et al.,2010）Fig.6 Outflow fluxes for (a) Case A and (b) Case B at 6 RE geocentric.Logarithm O+ number density for (c) Case A and (d) Case B in x-z cut plane in the geocentric solar magnetospheric coordinates (modified from Brambles et al.,2010)

在比较Case A 和Case B 模拟中O+离子外流对磁层位型的影响前，要先分析两种条件下离子外流在磁层空间分布的差异，主要是O+离子外流在磁尾到达位置的区别.在Case B 中，由于离子场向速度较慢，O+离子外流羽状流相对Case A 会更加偏向极区.这些O+离子外流是通过使用DC 坡印廷通量的经验公式（1）在极尖区域产生后，被输运穿过极冠并进入磁瓣，在那里它要么进入等离子体片并通过对流进入内磁层，要么从磁尾流出.进入内磁层的结果与Kistler 等（2010）中的Cluster 观测结果一致.如图6c、6d 所示，Case A 的初始场向速度较快，因此外流的等离子体主要流向远磁尾；但Case B 场向速度较慢，更多的外流离子会填充等离子体片和内磁层.这些结果与粒子模拟一致，即温度为100 eV 和场向速度为50 km/s 的O+离子将主要流向远磁尾，而温度为1 eV 和场向速度为3 km/s 的离子将主要向下流动进入等离子体片，在那里它们被加热到高能粒子，并会影响环电流（Ebihara et al.,2006）.

磁尾重联位置的改变减少了太阳风H+离子进入内磁层的途径.在IMF 南向的间隔期间，太阳风通过极尖区进入内磁层，然后通过磁瓣和等离子体片进行对流运输（Pilipp and Morfill,1978; Siscoe et al.,2001），其中等离子体片是地球夜侧发生重联的高温、稠密的等离子区.在这个特殊的磁暴事件中，刚开始来自太阳风的等离子体主要沿着极尖区—等离子体幔—磁瓣这条路径充满了等离子体片.然而，从极尖区到等离子体片的外流路径也取决于夜侧重联X 线的位置.如图7 所示，当存在电离层O+离子外流时，X 线的位置会发生变化.如果沿着该路径上的离子平行速度和垂直速度之比（v‖/v⊥）仅微弱地依赖于磁尾重联的位置，那么当磁尾重联区域向地球靠近时，太阳风等离子体进入等离子体片的通道相应地减少了.这种减少降低了来自太阳风的H+离子对内磁层的等离子体密度和压力的贡献.Brambles 等（2010）还提到Case A 中的v‖/v⊥与标准模拟大致相同，但随着重联X 线位置向地球内移，Case A 在内磁层中的累积的H+等离子体密度和压力的累积比标准模拟低约50%（未展示）.

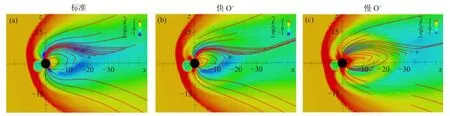
图7 （a）标准模拟；（b）Case A 和（c）Case B 以质子质量归一化后的流体密度.图中均是地心太阳磁层坐标系的 x-z 切面的结果，红线是磁力线，夜间重联X 线的大致位置用“+”符号标记（修改自Brambles et al.,2010）Fig.7 Logarithm density of the total fluid,normalized to proton mass for (a) baseline;(b) Case A and (c) Case B,in the x-z cut plane in the geocentric solar magnetospheric coordinates.Select magnetic field lines are superimposed on top of the mass density.Approximate location of nightside X-line is marked by a "+" symbol (modified from Brambles et al.,2010)

在Case B 中，对流输运到内磁层的O+离子抵消了由于H+离子数量减少而导致的等离子体压力降低.在距离地心大约6RE的内部磁层中，O+离子的数密度约为3 cm−3，而H+离子的数密度约为10 cm−3.模拟的“暴时”内磁层成分与Cluster 卫星的观测结果基本一致（Kistler,2016; Kistler and Mouikis,2016; Kistler et al.,2016）.内磁层中等离子体压力分布的变化改变了环电流，进而影响Dst 指数.图8a显示了真实Dst 指数与标准模拟、Case A 和Case B 模拟的虚拟Dst 对比.模拟的虚拟Dst 考虑了磁层所有电流的贡献，是基于Biot-Savart 定律用地球z 分量扰动计算的：

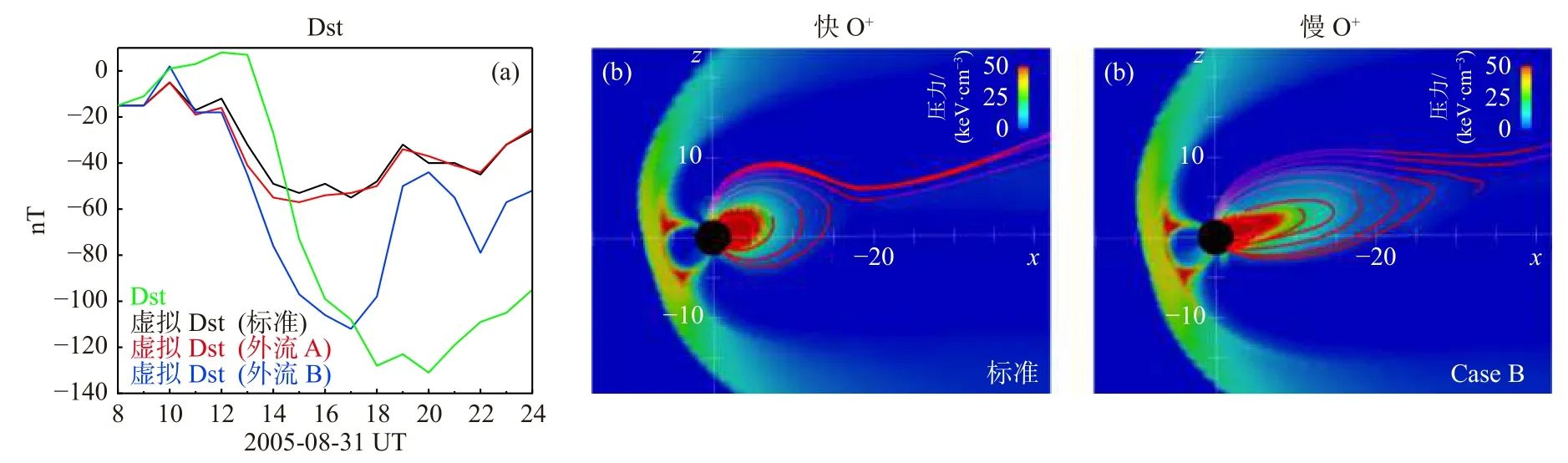
图8 （a）真实Dst 指数（绿线）与标准模拟（黑线）、Case A（红线）和Case B（蓝线）中的虚拟Dst 指数.（b）Case A 和（c）Case B 在 GSM x-z 平面中的总等离子体压力，红线为夜间磁力线（修改自Brambles et al.,2010）Fig.8 (a) Dst (green line) and pseudo Dst for baseline (black line),Case A (red line) and Case B (blue line).Total plasma pressure for (b) Case A and (c) Case B in the x-z plane in the geocentric solar magnetospheric coordinates with selected nightside magnetic field lines (modified from Brambles et al.,2010)

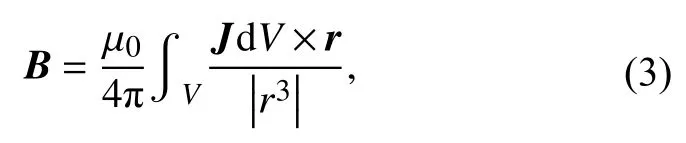
其中J是模拟的电流密度，dV是计算单元体积，r是指向计算单元中心的矢量.积分是通过对磁层域内所有计算单元的贡献求和来完成的.尽管内磁层中的H+离子减少了，由于内磁层中有电离层外流的O+离子，Case A 中的虚拟Dst 指数只比标准模拟略低10%.标准模拟和Case A 模拟的虚拟Dst 指数均与观测的真实Dst 指数存在较大差异.但是在只加了缓慢冷O+离子外流的模拟中（Case B），虚拟Dst 与观测Dst 有着相似的幅度.Case B 虚拟Dst 的强度超过标准模拟两倍，达到约−110 nT，接近−137 nT 的真实Dst.但是相比真实Dst，虚拟Dst 存在更多的动态结构，并且比恢复得更快.当南向的 IMF 短暂向北转时，虚拟Dst 在1700 UT 开始恢复.而真实Dst 持续下降直到2000 UT，并且衰减得更慢.

与标准模拟相比，Case B 的虚拟Dst 降低了，因为大部分从极尖区流出的O+离子聚集在内磁层中.当外流离子温度较低且速度较慢时（Case B），它会在对流环流中被加热并填充夜间闭合磁力线区域（图7c），从而导致更大的径向压力梯度.增加的压力梯度会产生更大的抗磁环电流，从而降低虚拟Dst.而当外流离子的温度较高且速度较快时（Case A），大部分外流O+离子会直接流向远磁尾损失掉，很少流入等离子片或内磁层改变抗磁环电流，因此对应的虚拟Dst 并没有显著降低.Case B 的压力梯度和环电流大约是与标准模拟或Case A 的两倍.

Case B 中增强的环电流也会影响磁尾磁场的拓扑结构，如图8c 所示.图8b、8c 是从电离层参考高度磁纬60°～90°相同位置追踪的磁力线.强抗磁环电流在环电流的尾部产生正的Bz，进而产生垂直于重联电流片的增强磁场.夜侧重联位置由于环电流和垂直分量增强而向磁尾移动.如磁暴模拟1500 UT 的瞬时结果所示，在标准模拟中，夜侧重联发生在大约21RE处；在Case B 中，它发生在大约36RE处.另一个可能的贡献因素是内磁层和等离子体片中压力的增加拉长了夜侧磁通量管并将重联X 线向后移动.在Case B 中，磁尾中 H+离子的v‖/v⊥增加了大约3 倍，这意味着尽管重联向后移动，但太阳风离子进入等离子片的通道却减少了.当南向的IMF 在1700 UT 时向北转向时，磁力线会重构位型.由于磁暴期间磁层对流过程的加剧，内磁层中约30%的O+离子密度在日侧边界处损失.O+离子损失导致压力梯度的降低和虚拟Dst 的早期恢复.亚暴过后，半球O+离子外流率降低到磁云层主序期间其值的25%左右.因此，此时O+离子外流对磁层的影响减弱，夜间磁力线恢复到与标准模拟相当的位型.

与Case A 和标准模拟相比，Case B 中内磁层中压力梯度的增强显著降低了虚拟Dst.在其他全球模拟中也可以看到这种效应（Glocer et al.,2009;Yu and Ridley,2013a,2013b）.然而，在MHD 模型中没有漂移动力学环电流的物理过程，即模拟中内磁层受对流过程而不是梯度曲率漂移动力学控制，这将导致环电流在全局MHD 模拟中衰减过快.将环形电流模型Rice 对流模式（Rice Convection Model,RCM）与全局模拟耦合可能会改进此处环电流的恢复相过程.该模式未考虑的共转效应也可以减少环电流的衰减.共转磁力线上的等离子体不应受到磁暴对流扰动的影响，因此内磁层的等离子体压强损失会更小.然而，我们预期，共转效应的影响相比梯度曲率漂移动力学的作用会很小.

2 对夜侧磁层对流模式的影响

当磁层顶重联期间太阳风等离子体和能量进入磁层后，部分物理和能量会储存在磁层磁瓣区域，并在之后释放到内磁层和电离层.根据驱动条件，磁层对流模式会有不同的响应，一般分为稳态磁层对流 （steady-state magnetospheric convection,SMC）、孤立亚暴（isolated substorm）和锯齿振荡（sawtooth oscillation）等三种类型（DeJong et al.,2009）.孤立亚暴的存储—释放过程只发生在局部且是一个孤立事件，各SM/IMF 驱动、极盖区开放磁通量（Fpc）和地磁AL 指数只有一次显著的振荡（图9c）.如果亚暴引起的能量存储—释放过程发生在全局且具有准周期性，那么这就被认为是一次锯齿振荡.如图9a 所示，锯齿振荡事件中，SM/IMF驱动尤其是IMFBz有周期性振荡，Fpc有长时间的持续响应而AL 指数也存在一定的周期性扰动.而SMC 期间，能量不被存储或释放，而是不断转移，磁层对流是准稳态的，其对应准稳态的SM/IMF 条件、Fpc和AL 指数.而电离层离子外流在磁层的分布决定了O+离子是否参与磁尾质量加载（mass loading）和重联过程，从而进一步改变磁层对流模式.

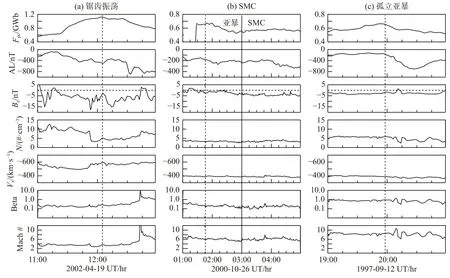
图9 三种对流模式中电离层和太阳风参数.（a）2002 年4 月19 日1205 UT（虚线）开始的锯齿振荡.Beta：太阳风等离子体Beta 值，热压比磁压；Mach：太阳风阿尔芬马赫数，太阳风速度比阿尔芬速.（b）2000 年10 月26 日的稳态磁层对流（SMC），开始于实线所示的0300 UT.SMC 之前的2 小时的虚线表示驱动SMC 的亚暴扩张的开始.（c）1997 年9 月12 日发生的孤立亚暴，开始时间为1158 UT（修改自DeJong et al.,2009）Fig.9 Stack plots of the ionospheric and solar wind parameters for each convection mode.(a) The sawtooth injection on 19 April 2002 with an onset at 1205 UT shown by the dotted line.(b) The steady-state magnetospheric convection (SMC) on 26 October 2000.The onset time of SMC is at 0300 UT shown by the solid line.Also plotted in the 2 h preceding the SMC the dotted line indicates the onset of the expansion of the substorm that initiates the SMC.(c) The isolated substorm that occurs on 12 September 1997 with an onset time of 1158 UT (modified from DeJong et al.,2009)

在本节中，我们关注O+离子外流对太阳风—磁层—电离层系统对流状态的影响.Wiltberger 等（2010）发现，当极尖区O+离子外流与夜间重联区相互作用时，它可以在稳态南向IMF 条件驱动的全球MHD 模拟中引发孤立亚暴.Wiltberger 等（2010）的模拟中，在产生第一次孤立亚暴之后，大部分O+离子落在新磁尾重联X 线的尾部，最终直接流出磁尾，基本不参与磁尾动力学，因此O+离子外流与太阳风—磁层—电离层系统的相互作用显著降低，磁层进入新的SMC 模式，类似于上一节中讨论的快速O+离子模拟（Case A）.在本节中，我们展示了电离层O+离子外流会导致卫星观测到的磁层对流锯齿振荡模式.这一条O+离子外流的反馈回路为研究影响磁层对流模式的产生机制提供了一个全新的重要概念.

在本节中，全球模拟中O+离子外流也是由一个经验公式确定.与上一节所介绍的模拟方法不同的是，该经验公式来自FAST 卫星观测的O+离子外流与向下阿尔芬交流（alternating current,AC）坡印亭通量之间的相关性，如Brambles（2012）中图2.3 所示.该O+离子外流数密度与向下流动的AC 坡印亭通量S‖之间的对应关系为：

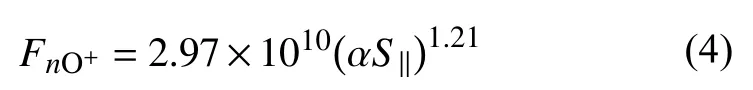
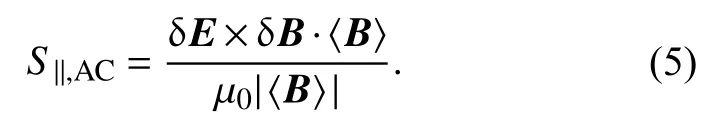
式中带通滤波电场 δE和磁场 δB是用全球MHD 模拟中的瞬时场E和B减去平均场〈E〉和〈B〉得到的.平均场则由5～180 s 带通平均的方法来计算，对应此层的Pc5 波动过程.有关计算AC 坡印廷通量的方法可参考Zhang 等（2012）.AC 坡印廷通量表征阿尔芬波能量，与引言中提及的影响O+离子横向加速的波粒相互作用有关.此处O+离子外流经验公式并不像上一节中使用的DC 坡印亭通量经验公式那样将外流限制在极尖区，主要分布在日侧极尖区.如图10 所示，AC 坡印廷通量调制的O+离子外流主要分布在模拟极光区，峰值在午夜前扇区.O+外流通量的这种晨昏不对称是由模拟AC 坡印廷通量的不对称分布引起的，这是因为电子沉降的不对称会导致电离层霍尔电导率的梯度从而产生对流模式的偏转（Zhang et al.,2012; Lotko et al.,2014）.这种不对称的夜侧外流结构类似于Polar 卫星观测的AC 坡印亭通量（Keiling et al.,2003）和FAST 卫星测到的O+离子外流通量（Chaston et al.,2007）的统计图.然而，这一系列的模拟没有重现卫星在日侧极尖区经常观测到的持续O+离子外流通量，这种差异可能是由于模拟中使用恒定的太阳风条件导致日侧磁场扰动过小.与DC 坡印廷通量模型不同，AC 坡印廷通量模型不会产生显著的日侧磁场时变扰动和流入电离层的阿尔芬波能量（Zhang et al.,2014）.

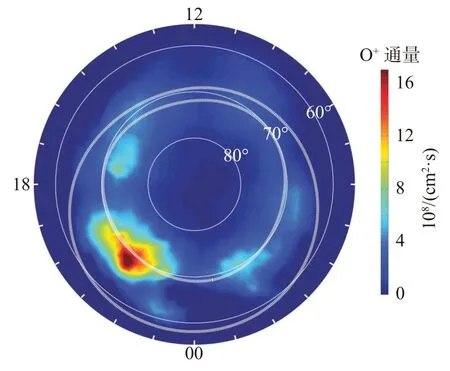
图10 Case C 的平均离子外流通量形态以及Feldstein 极光椭圆形（白色）（Feldstein and Starkov,1970）.作为参考，使用为常数的假设将外流通量沿磁力线映射到电离层高度（修改自Brambles et al.,2011）Fig.10 Morphology of average ion outflow from simulation C after the simulation start-up period,together with The Feldstein auroral oval (white) superposed (Feldstein and Starkov,1970).For reference,the flux has been mapped along field lines to the ionosphere using as constant along the dipole magnetic field of the Earth (modified from Brambles et al.,2011)

在该模拟中，O+离子外流场向速度和温度在磁层内边界处随空间和时间是恒定的，分别为45 km/s和100 eV.为了探究O+离子外流对全球磁层对流的影响，Brambles 等（2011）计算了对流模式对半球积分O+离子外流率（#/s）的依赖性.表1 中列出的所有模拟在使用表格中参数之前，都需要4 小时的磁层初始化，先2 小时北向IMF（Bz=5 nT），再2 小时南向IMF（Bz=−5 nT）.经验O+离子外流模型在这4 小时初始化结束以后再立即打开.

表1 不同α（不同半球流出率）的控制模拟列表.偶极倾角为零.太阳风数密度和温度恒定在5 cm−3 和10 eV.最后一列列出的外流率来自每次模拟的20 小时平均值（结果来自Brambles et al.,2011）Table1 List of controlled simulation with varying α (different hemispheric outflow rates).Dipole tilt angle is zero.The solar wind number density and temperature are constant at 5 cm−3 and 10 eV.The outflow rate listed in the last column is derived from a 20-hour average in each simulation (Results are from Brambles et al.,2011)

在α=1（无缩放）、VSW=400 km/s 和IMFBz=−10 nT 的条件下，经验外流模型计算出的球积分O+离子外流率为0.46×1026#/s.而基于卫星观测的统计研究中，强南向IMF 驱动条件下半球O+离子外流率约为1026#/s （Cully et al.,2003），这表明经验模型中的O+离子外流与观测统计结果基本一致.因此，表1 中列出的不同α条件下的模拟外流率均在统计观测结果的浮动范围内.

标准模拟中的磁层（无外流，α=0）处于SMC 状态.在这个没有O+离子外流的标准模拟中，在地心往磁尾约25RE的夜侧等离子体片区域发生了磁尾重联.在加入O+离子外流的模拟中，增加的磁层等离子体使磁尾膨胀并使磁重联位置进一步向后移动.在α=1 的模拟中，磁尾呈现更动态的结构，夜侧重联向后移动到30～45RE之间的位置.尽管磁尾结构变得更加动态，但整个系统仍处于活跃的SMC 状态，对流模式没有变化.随着半球O+离子外流率从1.18×1026#/s 增加到9.46×1026#/s，夜侧磁力线被拉伸得更长，并且夜侧重联进一步后移到50～65RE.这种磁尾拉伸源于外流的O+离子进入等离子片而额外产生的等离子体压强.该过程同时增强了压力梯度力和抗磁环电流，这会通过改变磁尾的受力平衡来影响磁场.这两种效应都会使磁通量管膨胀和受压.这与上一节Case B 模拟中的效应相似，因为大部分夜间O+离子外流物质进入等离子层和内磁层中.当O+离子外流率足够大时，夜间磁通量管被压缩，这种不平衡的磁场张力会激发等离子体喷射.这种储存能量的释放表现为亚暴，但与孤立亚暴事件完全不同.在这种由O+离子质量加载激发的磁层亚暴中，大部分O+离子于亚暴对流期间在直接流向等离子体层下游与远磁尾直接损失掉，或通过电场漂移输运到磁层顶位置因重联而损失（Zhang et al.,2017）.剩下一部分夜侧电离层外流的O+离子则在亚暴过后又回到夜侧重联区.随着外流O+离子重新充满了内部磁层，再次拉长了磁力线，并在几个小时内导致了另一场亚暴，从而产生周期性的磁层亚暴过程，这就是由电离层O+离子外流引起的磁层锯齿振荡模式的基本物理过程，如图11 所示（该图来自表1 中的Case C）.

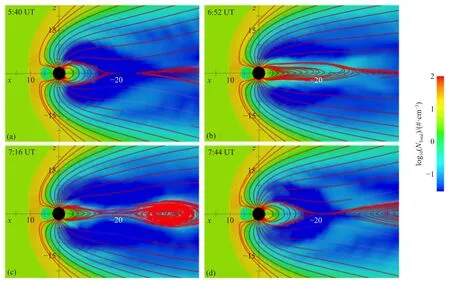
图11 Case C 中一次振荡的锯齿机制.背景颜色是总等离子体数密度的对数，叠加的红线是磁力线，结果是中午—午夜平面.不同子图表征了（a）初始状态、（b）离子外流引起磁力线拉伸、（c）等离子体释放和（d）恢复相的结果（修改自Zhang and Brambles,2021）Fig.11 Sequence showing the sawtooth mechanism for one oscillation from run C.Background color is logarithm of total plasma number density with magnetic field lines superimposed in red,taken in noon-midnight plane.Plots show (a) initial state,(b) stretched field lines caused by influence of ion outflow,(c) release of plasmoid and (d) return to the initial configuration(modified from Zhang and Brambles,2021)

对模拟结果的进一步分析显示，地球同步轨道附近的磁倾角呈现明显的周期性锯齿波变化.图12显示了用于估计亚暴周期性的磁倾角模拟时间序列，并将模拟结果与卫星数据中观察到的锯齿亚暴进行了比较.表1 中列出的标准模拟Case 0 和Case J 为SMC 状态，而其他三个模拟（Case C、H 和I）表现出随着磁倾角的周期减小和幅度增加的锯齿振荡.这些模拟表明，随着半球O+离子外流率的增加，在多流体全球MHD 模拟中磁层逐渐从SMC 转变到锯齿振荡的状态.观测到的SMC 和锯齿振荡状态都需要准稳定的太阳风来驱动，但发生锯齿振荡时对应的太阳风驱动比SMC 时幅度更大（DeJong et al.,2009），这与模拟一致.从表1 中列出的数值实验来看，超过1.1×1026#/s 的积分外流率是在强烈的稳态上游驱动条件下发生锯齿振荡的必要条件.请注意，用于激发锯齿模式的外流率下限仅适用于O+离子外流经验公式驱动的理想模拟.基于顶部电离层物理模型的O+离子外流模拟表明，除了半球外流率，O+离子源位置的空间分布在调节磁层对流模式方面也起着重要作用（Varney et al.,2016a,2016b）.

图12 模拟磁倾角 θ=随模拟时间的变化.结果取自2330 MLT、=6.6RE，z=0.5RE的位置.表1 中列出了模拟Case 0、C、G、H 和I 的比较.“0 小时”的基准开始时间为两小时南向IMF 初始化结果的时间（修改自Brambles et al.,2011）Fig.12 Simulated magnetic inclination angle θ=,as a function of simulation time at 2330 MLT,=6.6RE,z=0.5RE.Comparisons are shown for runs 0,C,G,H,and I listed in Table 1.The fiducial start time of "hour 0" begins at the end of a two hour southward-IMF pre-conditioning period (modified from Brambles et al.,2011)

真实的太阳风—磁层—电离层耦合系统远比模拟中要复杂，因此太阳风/IMF 驱动条件、O+离子外流率、锯齿振荡与SMC 状态之间的关系需要通过观测结果来检验.与孤立亚暴相比，磁层锯齿振荡模式的一个显著特点是发生磁力线拉伸和偶极化等特征的磁地方时（magnetic local time,MLT）范围更广.通过比较表1 中所示的所有模拟的锯齿磁暴事件磁倾角与观测锯齿事件的历元分析，可以研究锯齿亚暴的空间拓展（Cai et al.,2006）.图13 所示模拟的锯齿振荡和在地球静止卫星上观察到的锯齿亚暴磁倾角的对比.在模拟中的磁倾角在切面z=0.5RE和=6.6RE的圆上估算.对于每个观测的锯齿亚暴，偶极化开始时间（对应模拟基准时间“0 UT”）的选择用类似于 Cai 等（2006）使用的方法，即2330～0030 MLT 扇区磁倾角快速增加之前最后一个极小值的时间.

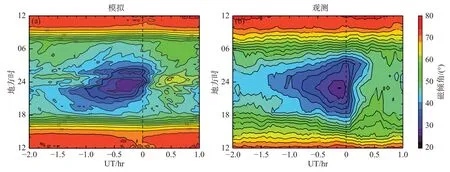
图13 （a）模拟和（b）观测锯齿磁暴期间地球静止轨道附近磁倾角的历元分析（修改自Brambles et al.,2011，观测来自Cai et al.,2006）Fig.13 Superposed epoch analysis of magnetic inclination angle near geostationary orbit for (a) simulated and (b) observed sawtooth(modified from Brambles et al.,2011,the observed results from Cai et al.,2006)

图13 表明，模拟结果和观察结果有很多的相似性：数值模拟中的平均最小倾角为27°，而观察到的锯齿事件中的最小倾角为26°，两者均低于地球静止轨道上观测到的孤立亚暴平均值的最小倾角43°（Cai et al.,2006）.观测和模拟的磁倾角锯齿波变化在地球静止轨道上比孤立亚暴有更剧烈的变化特征，详见Cai 等（2006）.并且两者都表现出晨昏不对称性，在午夜前的区域具有更明显的特征.模拟起始点的不对称性由图10 中所示的外流分布不对称性引起.虽然模拟得到的锯齿振荡的MLT范围略小于观测值；例如模拟锯齿中0 UT 处的44°轮廓跨越10 小时的MLT，而观察到的锯齿的MLT 为12 小时，但是模拟中的锯齿振荡MLT 范围仍然远大于Cai 等（2006）报道的孤立亚暴2 小时的平均MLT 范围.

在本节的后续部分中，Brambles 等（2013）使用一个基于真实事件（2002 年4 月18 日的磁暴）的模拟为例来论证在空间天气事件全球模拟中电离层O+离子外流的重要性，尤其是重现观测到的准周期亚暴事件.尽管2002 年4 月18 日的7 次连续锯齿注入已被广泛研究（如，Huang,2002; Lui et al.,2004; Henderson et al.,2006; Kitamura et al.,2011），但其产生与触发机制仍不清楚（Lee et al.,2004; Huang,2011）.因此该事件的全球模拟，是电离层O+离子外流对产生锯齿亚暴的重要性的一个很好的例证.

2002 年4 月18 日的磁暴事件是由磁云产生的，该磁云是4 月17 日至24 日期间影响地球的一系列行星际日冕物质抛射（coronal mass ejection,CME）.图14 显示了磁暴期间测量的SW/IMF 数据，其作为上游边界条件来驱动全球模拟.2002 年4 月18日0～4 UT，太阳风等离子体密度和动压突然增加，IMF 由北向转为南向.在0400 UT 之后SW/IMF 条件几乎没有变化，密度较低，具有相对稳定的超音速和南向的强IMFBz.该磁暴被归类为中等太阳风暴，最低Dst 指数为−130 nT.尽管有这些相对稳定的太阳风条件，但地球静止卫星的同步带状粒子分析仪仍然测到了7 次周期性粒子注入（Henderson et al.,2006）.

图14 2002 年4 月18 日磁暴在全球磁层模拟中用作上游边界条件的太阳风参数（修改自Zhang and Brambles,2021）Fig.14 Solar wind parameters for the 18 April,2002 storm used as upstream boundary condition in the global magnetosphere simulation (modified from Zhang and Brambles,2021)

通过比较未添加外流效应的标准模拟与添加了电离层O+离子外流效应的控制模拟，可以研究在真实空间天气事件中电离层O+离子外流对磁层的影响.使用本节讨论的由AC 坡印廷通量控制的O+离子外流经验模型对外流通量进行建模，等式（4）中的α值取3.8，该值是根据表1 中列出的理想化数值实验的结果选择的.在α=3.8 时，模拟得到的磁层在弱太阳风电场驱动下呈现准周期对流，在强太阳风电场驱动下呈现准周期亚暴.值得注意的是，2002 年4 月18 日磁暴产生了一序列7 次周期性亚暴，该亚暴在许多地球物理过程中都被观察到.观测数据和模拟结果之间的比较仅限于全球模拟中可用多流体MHD 方程描述的地球物理过程.

图15 显示了观测数据、标准模拟和外流模拟之间的（a）极盖区和（b）磁尾磁通量的比较.极盖区磁通量的观测结果是使用极地航天器上远紫外成像仪的数据得到，磁尾中开放磁通量的观测数据则是使用Geotail 的等离子体和磁场数据计算得到，具体计算详见Huang 和Cai（2009）.模拟的极冠区通量通过跟踪瞬时磁力线来计算，以区分开放和封闭磁场边界的分界线的位置，然后映射到电离层.最后使用对北半球数据面积分来计算通过封闭表面的磁通量.

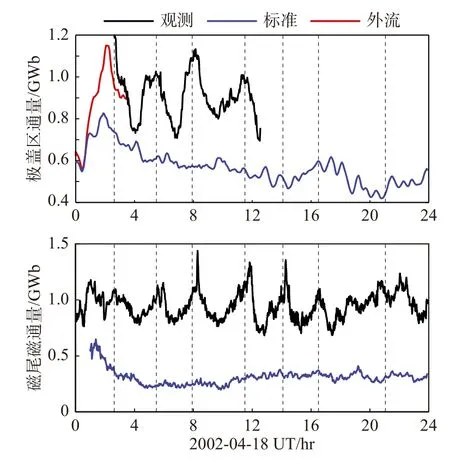
图15 观测（黑线）、无外流模拟（蓝线）和有外流模拟（红线）中的磁通量.（a，b）分别是电离层和磁尾的结果.垂直虚线显示外流模拟中的亚暴开始.观测结果来自Huang 和Cai（2009），图修改自Brambles 等（2013）Fig.15 Magnetic flux for observed (black) taken from Huang and Cai（2009）,the baseline simulation without outflow (blue) and the controlled simulation with outflow (red),calculated at the ionosphere (a) and magnetotail (b).Vertical dashed lines show substorm onsets in the outflow simulation.Figure from Brambles et al.(2013)

外流模拟中的开放磁通量表现出周期为2～3小时的锯齿振荡特征.尽管模拟中的开放磁通量与观测数据中的开放磁通量不同，但两者的加载/卸载周期是相似的.相比之下，标准模拟中的极冠区通量只有一个加载/卸载周期，然后从0200 UT 到1600 UT 保持相对稳定.标准模拟中磁通量只有约30～60 min 时间尺度上的变化，这可能是由不规则的磁尾重联产生的（Goodrich et al.,2007）.图中的垂直线对应于外流模拟开放磁通量大幅下降的开始时间.模拟结果表明产生第一个亚暴不需要电离层外流，因为标准模拟在0156 UT 的开始时间早于外流模拟的时间（0216 UT）.这一结果与Wiltberger等（2010）的一致.Wiltberger 等（2010）也发现等离子体片中大量源自电离层的O+离子会延迟亚暴开始时间.与标准模拟不同，O+离子外流模拟随着时间的推移会产生一系列锯齿振荡模式，从0652 UT、0920 UT、1302 UT 和1520 UT 四个时间点开始，都可以在极盖区和磁尾磁通量中看到，相应的标准模拟则没有出现明显的周期性亚暴特征.虽然外流模拟中每个亚暴的时间都比等效观测到的亚暴晚了大约 1 小时 20 分钟，但亚暴的后续周期（约2:45 小时）是相似的.在0000 UT 和1600 UT 之间，在极盖区和磁尾中计算的磁通量分布显示出相似的分布.

图16 对比了GOES 8 和GOES 10 卫星测量的磁场.与GOES 8 和GOES 10 的测量结果相比，外流模拟中计算的Bz分量比标准模拟有显著改进.在GOES 8 和GOSE 10 卫星结果中的Bx和Bz都可以看到周期性亚暴的特征.然而，在外流模拟中，只有Bz呈现出该周期性.注意这只是一个特定事件，虽然在全球模拟中需要O+离子外流来产生准周期性亚暴，但这并不一定意味着外流是锯齿数据库（Cai and Clauer,2009）中所有周期性亚暴事件的原因.许多此类事件的周期性亚暴很可能是由太阳风的周期性变化驱动的，而不是由电离层外流对夜间重新连接的影响所驱动.例如，数据库中的一些锯齿事件是在高速流与高速流交互作用区域发现的（Cai et al.,2011）而不是在CME 事件中，这超出了本文的讨论范围.

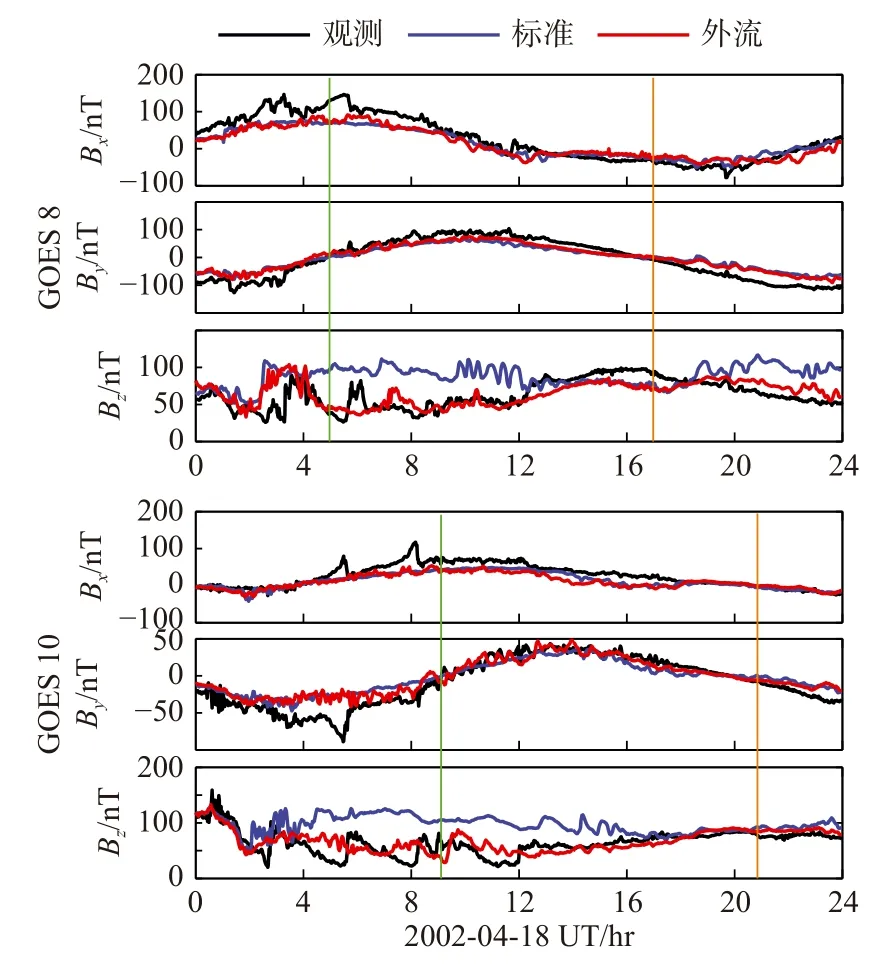
图16 GOES 8 和 GOES 10 探测的（黑）、标准模拟（蓝）和外流模拟（红）的磁场（修改自Brambles et al.,2013）Fig.16 Comparison of magnetic field taken at GOES 8 and 10(black) with simulated magnetic fields at GOES 8 and GOES 10 for the baseline (blue) and the outflow (red)simulations (modified from Brambles et al.,2013)

3 总结和展望

当太阳风驱动磁层产生强对流和粒子沉降时，电离层O+离子可能会被加热为超热离子而外流到磁层.该外流的超热O+离子会对太阳风—磁层—电离层耦合系统的动力学过程有显著影响.电离层外流入磁层的O+离子存在“速度过滤效应”，即外流离子的分布由离子外流速率决定.一般来说，场向速度较快（50 km/s 量级）的外流O+离子更倾向于直接流到远磁尾区域并损失掉，这部分外流离子对磁层动态结构的影响相对较弱.而场向速度较慢的（3 km/s 量级）的外流O+离子会主要落在等离子片区域内，这会显著影响环电流、质量加载和重联过程，从而改变磁层物质成分和磁场拓扑结构.电离层O+离子外流与夜侧重联区相互作用，除了可能引发磁层对流的孤立亚暴外，还可以引起周期为2～3 小时的锯齿振荡对流模式.整体上，目前研究对于电离层氧离子外流以及对磁层影响的认识还处在初步阶段，还有一系列问题亟需研究：

（1）厘清离子加速机制的物理过程.目前理论认为电离层O+离子进入磁层需要上行和外流两个步骤.O+离子上行由焦耳加热和软电子沉降导致，但是这两个过程只能使离子抵达顶部电离层，而没有足够能量使得O+离子逃逸或外流到磁层.因此还需要无碰撞的波粒相互作用来加热O+离子，使其横向加速获得外流的磁镜力.但目前无论是观测还是模拟缺乏对以上过程的定量分析.由于电离层—磁层系统中多物理过程的耦合，少量的观测数据很难分离驱动上行或外流的物理过程，需要更多的全球不同圈层的观测.而目前的模拟主要还是使用经验公式来模拟外流过程，缺乏基于电离层基本物理过程的数值计算，比如用基本物理公式来模拟离子横向加热过程，这需要提升目前的物理模式.

（2）探究上层热层对离子外流的作用.热层中性密度不是一成不变的.比如强磁暴期间极尖区的热层中性密度会显著增强（Lühr et al.,2004），或者太阳活动变化导致固定高度面的中性密度、温度和风场变化（如，Hagan and Oliver,1985; Hedin and Mayr,1987; Hedin et al.,1994; Drob et al.,2015）.而热层中性密度的变化可能会影响光化学或其他复杂的物理过程，进而影响离子外流过程.这些物理过程都需要用不断发展的磁层—电离层—热层耦合模型来进一步研究.

（3）研究离子外流过程的天气学效应.如图2所示，电离层离子外流通过多种途径影响太阳风—磁层—电离层—热层耦合系统的动态变化.另一方面，耦合系统的动态变化会反馈影响外流离子群的产生和传播.因此，这些电离层源离子群在空间天气建模中发挥着重要作用，特别是对于地磁暴事件.例如，要了解电离层外流对日侧重联的影响，需要使用不同外部驱动条件下离子外流的真实模型，详细分析局部和全局重联率对电离层离子存在的依赖性，以量化在日侧重联点，电离层离子的分布和进入路径，包括它们的时间变化.太阳风和磁层的相互作用作为电离层离子的空间分布浓度的函数是多物理场的，突出的问题包括相互作用如何受外流模型的影响，外流过程如何动态响应不断变化的重联率，环电流如何受这些外流离子群的调节，以及这如何受到外部驱动条件的影响.因此，需要多物理场、自洽模型来解决这些反馈机制，尤其是在不同类型的地磁暴期间.