1980—2017年漠河市降水量变化趋势及突变特征分析
2022-06-17张丽娜孙颖娜孔心雨
张丽娜,孙颖娜,孔心雨,陈 实
(1.黑龙江大学水利电力学院,黑龙江 哈尔滨 150080;2.黑龙江大学中俄寒区水文和水利工程联合实验室,黑龙江 哈尔滨 150080)
众所周知,我国淡水资源在时空分布上呈现东多西少、南多北少的特点,在季节上呈现春冬少、夏秋多的特点[1]。而降水作为水资源中举足轻重的元素,亦是水文循环中不可或缺的环节,对其变化趋势和突变情况的研究意义非常重大。在全球气候变化和城市化进程持续快速推进的影响下,短历时强降水造成的城市内涝灾害频繁发生,给人类社会造成了巨大的损失[2- 4]。如何高效管理和治理好水资源是人类长期面临的挑战和重要的任务。[5]
近年来,许多学者对漠河地区的水文变化特征进行了研究。桂翰林等[6]通过研究发现近几十年漠河市降水量呈现增大的趋势,张硕在前人的基础上,采用集合经验模分解(Ensemble Empirical Mode Decomposition,EEMD)和滑动t检验的方法[7],得出漠河市近60年年降雨量整体呈现上升的趋势,王春红等[8]则对漠河市的年、季气温做出了研究。上述研究有对该地区的年降水量变化趋势进行分析,也有季节性的气温变化研究,但对漠河市季节性的降水变化特征分析较少。因此,本文采用滑动平均法、Kendall秩次相关检验法、有序聚类分析法和游程检验法对漠河市1980—2017年的年降水量和冬季降水量的变化趋势和突变特征进行分析探讨,力求为漠河地区的水资源规划和利用提供理论依据。
1 研究区概况
漠河市位于黑龙江省西北部,大兴安岭山脉北麓[9],西与内蒙古自治区额尔古纳市为邻,南与内蒙古自治区根河市和大兴安岭地区所属呼中区交界,东与塔河县接壤,北隔黑龙江与俄罗斯外贝加尔边疆区(原赤塔州)和阿穆尔州相望,边境线长242km,总面积18427km2。漠河市是中国气温最低的县份,由于大陆及海洋季风交替影响,小气候变化多端,局部气候差异显著。冬季在极地大陆气团控制下,气候寒冷、干燥而漫长;夏季受副热带海洋气团的影响,降水集中,雨量充沛,气候湿热,日照时间长,适宜耐寒生作物生长,但易发生洪涝和低温冷害;春、秋两季,因冬夏季风交替,气候多变。春季多大风,降水偏少,物燥干旱,易发生森林火灾;秋季降温急剧,常有早霜和冻害发生。
漠河市年平均气温在-5.5℃,各月平均气温在0℃以下的月份长达8个月之久,气温年较差为49.3℃,平均无霜期为86.2d。年平均降水量为460.8mm,全年降水量70%以上集中在7月份,5—6月份为旱季,7—8月份为汛期。太阳辐射总量年平均为96~107kcal/cm2,日照时数为2377~2625h,≥10℃的积温1436~2062℃[10]。
2 数据来源与研究方法
2.1 气象数据
漠河气象站海拔433m,是我国纬度最高的气象站,始建于1957年[7]。本文所使用的气象数据由中国国家气象数据网下载,以漠河市1980—2017年的逐日降水量资料为研究数据。
2.2 研究方法
2.2.1趋势成分识别
(1)滑动平均法
滑动平均法又称移动平均法。滑动平均法通过削弱时间序列的滑动周期来体现时间序列的变化趋势[11]。用以下公式表达:
(1)
式中,k—滑动长度;yt—新序列值;xt—原序列值。
若xt序列本身具有一定的趋势,选取一个合适的k(不适宜偏大),此方法即可把趋势清晰地显示出来,故而该方法在业内被广泛地应用。
(2)Kendall秩次相关检验法
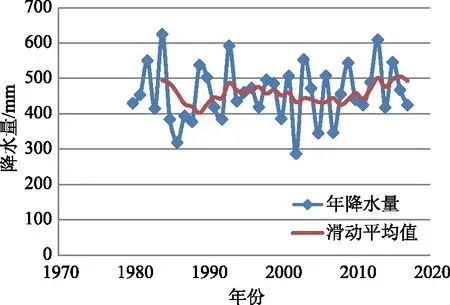
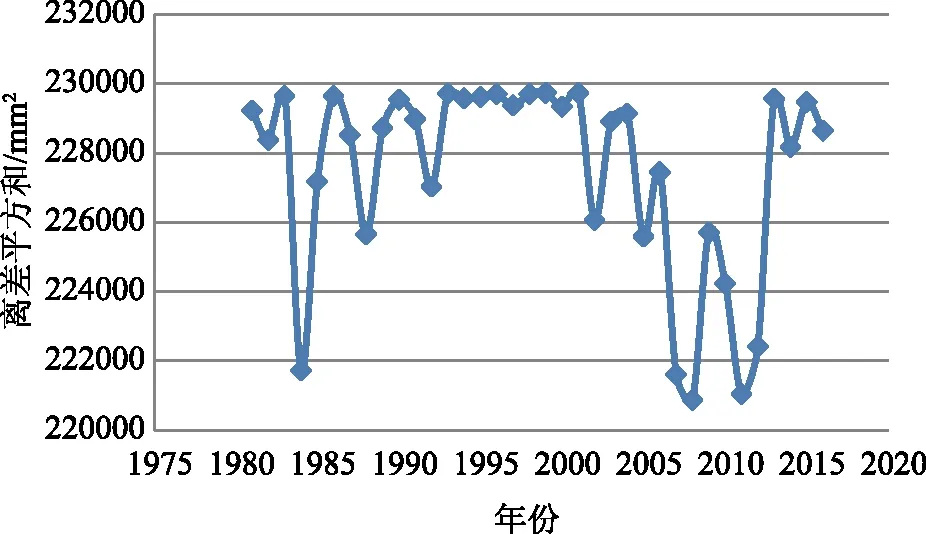
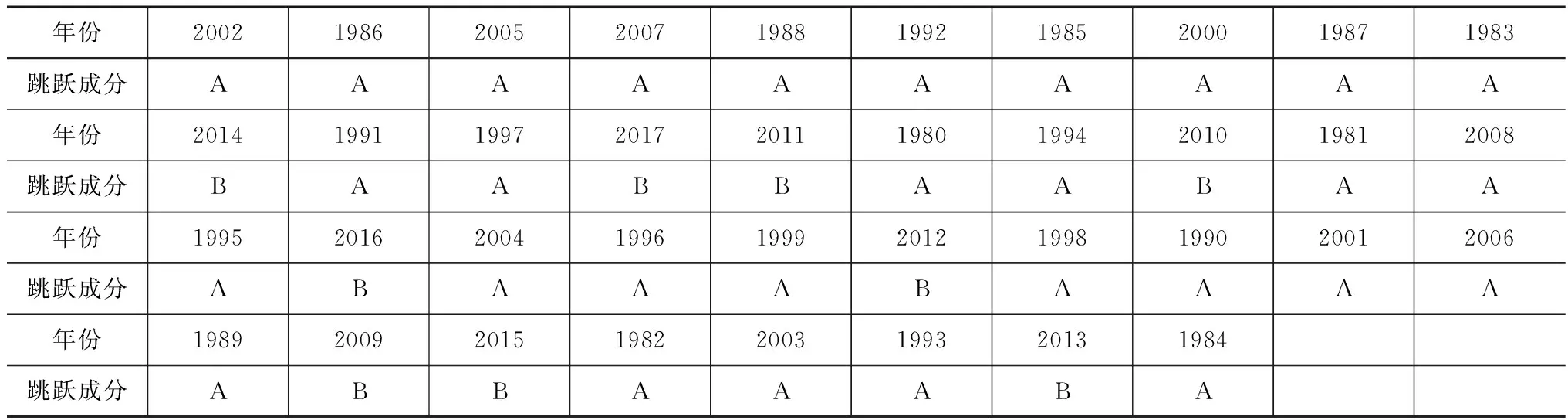
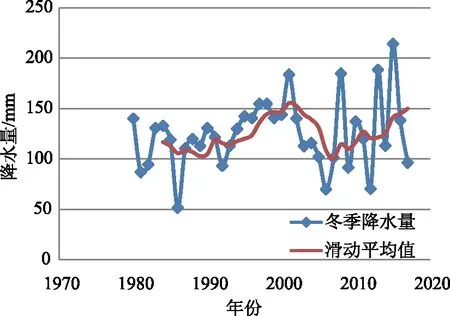
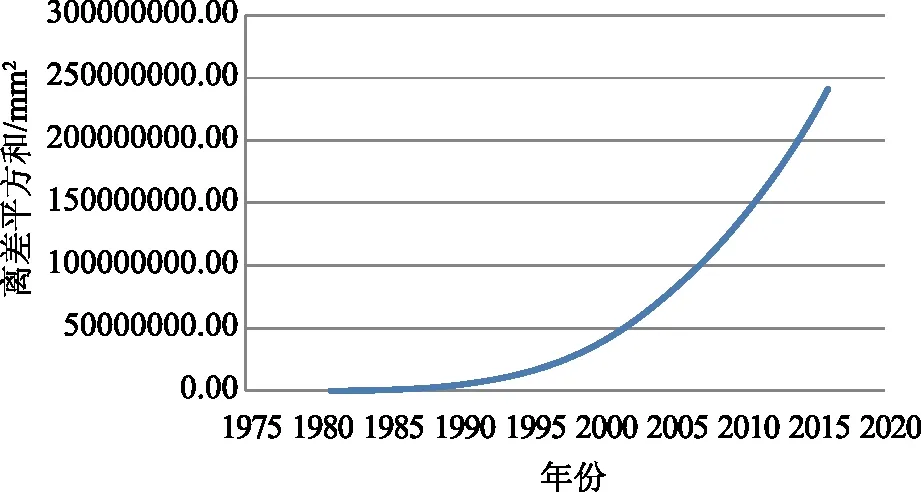
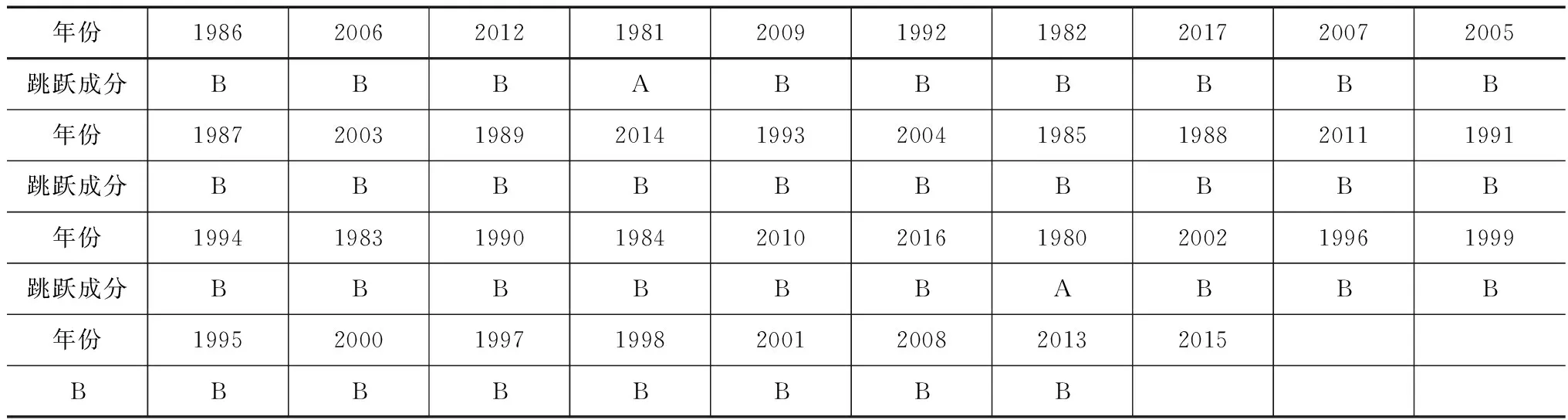
对于水文序列x1,x2,…,xn首先要找到每个数值的对偶值,即k。按照如下公式求得统计量,若|U| (2) 其中, (3) 式中,U—构造的统计量;k—序列中对偶观测值出现的个数;n—系列长度。 2.2.2跳跃成分识别和检验 2.2.2.1 突变点的识别和推断 目前确定突变点τ的方法主要有4种,一是从各种成因来确定的分析方法,二是时序累计值相关曲线法,三是有序聚类分析法,四是Mankendall法。本文详细讨论以下2种方法。 (1)时序累计值相关曲线法 时序累计值相关曲线法需要有合适的参证序列y1,y2,…,yn,研究序列则是列x1,x2,…,xn。将这2个序列的序累计值分别求出来: (4) (5) 式中,xt—研究序列;gi—xt的时序累计值;yt—参证序列;mj—yt的时序累计值。 点绘出mj与gj的关系图,如果研究序列Xt跳跃不显著,则mj-gj这个公式所对应的图像是一条直线,并且通过原点;反之这个图像就是一条折线,而那个转折点就是要求的突变点τ。 (2)有序聚类分析法 有序聚类分析方法是一种通过统计分析推估出水文时间序列最可能突变点的方法,然后结合实际情况进行具体分析。其主要的分割思想是使得同类之间的离差平方和最小,而类与类之间的离差平方和最大[12]。通过以下式子进行突变点计算: (6) (7) (8) 式中,S—定义的目标函数;τ—突变点。 当S取最小值时,与其所对应的τ为最优二分割点,可推断出突变点。 2.2.2.2 跳跃成分显著性检验 下述为游程检验法进行跳跃成分显著性检验的详细步骤。在水文序列中找出突变点,设突变点之前的个数是n1,突变点之后的个数为n2(n=n1+n2);把突变点之前的数值都标记为A,突变点之后都标为B,然后,把这水文序列的数值按从大到小排列,得出一串ABBA…的序列,记录A和B序列连续出现的次数之和,该值为称为游程数。 当n1、n2>20时,k趋于正态分布: (9) 式中,k—统计游程总个数;n1—突变点之前的个数;n2—突变点之后的个数;N—正态分布函数;U—构造的统计量。 由给定的显著性水平α后,得出Uα/2。当|U| 当n1、n2<20时,在显著性水平α条件下有临界值kα。当k≤kα时,拒绝接受原假设,即来自不同的总体,具有跳跃成分。 对漠河市该水文时间序列使用滑动平均法进行趋势拟合,采用滑动平均法得到结果如图1所示。1980—2017年漠河市降水量的最高值发生在1984年,为624.7mm,最低值发生在2002年,数值为286.8mm,多年平均降水量为457.0mm,整体的波动幅度比较大,流域降水年内分配不均[13]。五点滑动使得变化趋势更加明显:剧烈下降-剧烈上升-缓慢下降-缓慢上升。综合来看,该序列无明显的上升或下降趋势,而是基本持平的状态。 图1 漠河市1980—2017年年降水量趋势变化 利用坎德尔秩次相关检验法进行趋势变化显著性检验[14],对偶值求和得K=388,再将所得数值代入计算公式,即可得到结果:τ=0.1038;D(τ)=0.0128;U=0.917。 取显著性水平α=5%,查得Uα/2=1.96。由于|U| 为了精准确定漠河市年降水量序列发生显著变异的突变点,对该址水文降水序列采用有序聚类分析法,详细结果如图2所示。 图2 漠河市1980—2017年降水量离差平方和变化过程 由图2可知,该水文序列的有序聚类法函数值S除了在1993—2001年呈现出平稳的波动状态,其余年份的波动幅度都比较大,故可清晰地分析出S值的最小年份为2008年,即2008年为变异点。 现将该数据(2008年)进行跳跃成分检验,并将2008年以前记为A,2008年以后记为B,并对其进行升序排列,查出游程个数,见表1。 表1 游程检验法计算表 n1=29,n2=9,游程总数k=15,U=0.12。取显著性水平α=5%,查得Uα/2=1.96,|U| 对于漠河市1980—2017年的冬季降水量,其多年平均冬季降水量为124.8mm,最小值为51.5mm,最大值为214.2mm。采用滑动平均法对该水文序列进行变化趋势分析,如图3所示,呈现出明显的上升-下降-上升波动,但整体上并无上升或者下降趋势。 图3 漠河市1980—2017年冬季降水量趋势变化 对于漠河市冬季降水量的分析,可采用以上相同的方法来进行探讨,对水文序列资料的趋势变化显著性检验,将所有对偶值相加,得到K=388;τ=0.1038;D=0.0128;U=0.917。取显著性水平α=5%,查得Uα/2=1.96。由于|U| 对于漠河市冬季降水量序列采用有序聚类分析法来精准识别水文资料序列发生显著变异的年份。其变化趋势如图4所示,其清晰直观呈现出所求目标函数值S不断上升的过程,故1981年为突变点。 图4 漠河市冬季降水量离差平方和变化过程 游程计算结果见表2,n1=2,n2=36,游程总数k=5,U=0.39,取显著性水平α=5%,可得Uα/2=1.96,|U| 表2 游程检验法计算表 (1)1980—2017年漠河市年降水量多年平均值为457.0mm,整体上是一个升降交替的状态,其年降水量序列并没有明显的上升趋势或者下降趋势成分,也不存在跳跃成分。 (2)对于漠河市1980—2017年的冬季降水量,其多年平均冬季降水量为124.8mm,极差虽然比年际小,但整体上波动幅度较大,无显著趋势成分。以1981年为突变点,经过跳跃成分显著性检验后知该水文序列并无跳跃成分,故保持以上趋势分析结果。 (3)本文补充了漠河市的冬季降水量趋势及突变特征分析,填补了一部分该区域水文研究的空缺。在未来研究中,可适当延长水文序列、用多种方法来进行对比评估以及极端天气的研究。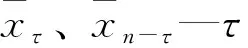
3 结果与分析
3.1 漠河市年降水量趋势分析与突变点特征分析
3.2 漠河市冬季降水量趋势与突变点分析
4 结语
