横向相关性及参数影响下的车道级交通预测

侯 越，崔菡珂，邓志远

(兰州交通大学 电子与信息工程学院，甘肃 兰州 730000)

0 引言

随着机动车保有量的持续增加，由拥堵引发的交通状况不仅随时间变化，更受制于空间复杂因素的影响，造成单维度下的短时交通预测准确率不高等问题。传统预测方法以整个路段为研究对象，未充分考虑不同车道在相同时间间隔内的参数分布情况及相关影响，使得预测模型无法精确估计交通运行状态。为提升预测模型的精度，通过横向车道间的空间相关性及宏观参数间的关系考量对交通流数据建模，使其能够准确刻画实际场景中的交通运行状态，具有非常重要的意义。

短时交通流预测的传统方法可分为两大类：统计学方法和机器学习方法。早期提出的ARIMA[1]主要用于模拟交通流时间序列的周期性变化，邱敦国等[2]提出SARIMA-RBF模型，相较于原有模型拥有较好的预测精度，但其缺陷在于处理随机事件时会发生易失效的问题。机器学习因其在非线性数据处理方面的优势被广泛采用，黄振盛等[3]建立支持向量机回归子模型，组合得到的模型相较于其他模型更为稳定。而深度学习具有提取复杂特征的能力且易实现分层建模，在交通大数据分析处理中较为常见，其方法有：循环神经网络(RNN)[4]、长短时记忆网络(LSTM)[5]、门控循环单元(GRU)[6]等。其中，LSTM和GRU凭借对历史数据保有记忆性，常用于解析交通流的时间特性。随着交通检测设备的多源化及数据驱动模型的长足进展，对交通大数据的治理提出了更高要求，李慧等[7]利用PCA主成分分析方法将交通流数据的主成分和随机噪声进行分离，降低噪声干扰；陆百川等[8]运用GA-WNN对微波、地磁、浮动车数据进行多源融合处理，提升了预测模型的精度，但由于未考虑空间特性，模型性能还有很大的提升空间。交通大数据处理分析中，时空规律及内在特征的挖掘，对于预测模型的优化至关重要，董春娇等[9]考虑了空间特性中车辆进出匝道时对交通流的影响；杜圣东等[10]通过LSTM与注意力机制的结合，考虑了区域空间相关性及时空依赖特征；Zhao等[11]提出ODC矩阵代表路网中路段间的相关性，将其作为LSTM的输入，实现对时空关系的分析；Gu等[12]通过LSTM和门控循环单元建立预测模型，以考虑车道间的相关性，在对车道级速度预测的过程中验证了模型的有效性。以上文献在空间特性方面着重于路段间的关系描述，而对车道间的横向相关性提及较少，Gu等[12]虽考虑了车道级的空间特性，但并未对宏观参数间的相互影响加以分析。本研究从横向车道级空间特性和宏观参数相关性出发，综合考虑交通流的时空变化特性，分析交叉口路段中多车道间的相互作用，并运用主成分分析法(Principal Components Analysis,PCA)提取多车道速度与流量特征，采用stacked-GRU对多车道特征参数进行验证。试验结果表明，考虑横向车道级空间相关性及宏观参数间影响的方案拥有更高的预测性能。

1 交通流时空特性与参数相关性分析

1.1 交通流时空变化特性

交通流的时间特性是指在某一断面上的交通流状态会随时间产生规律性的变化。在较长时间段上具有周期性(例如每月,每天)，而在较短的时间片内(如5 min)又具有时变性和随机性的特征。

交通流的空间特性是指在某一时刻交通流在城市道路网络上的分布情况。观测路段的交通流可知，其与周围可达路段间存在空间相关性，因此需考虑空间特性对该路段交通流的影响。在城市交通路网中，各个断面间存在空间相关性，现有研究已有较多文献对其进行分析[13]，而同一截面的车道间也存在相关性，如图1所示，不同车道间流量相互关联，同一空间中每一时间片的交通流都在变化，下一时间片与上一时间片也存在明显的关联，因此，综合考虑时空维度来分析交通流的变化，特别是横向相关性的影响，对预测模型的性能提升尤为重要。

图1 时空关系示意图Fig.1 Schematic diagram of spatio-temporal relationship

1.2 参数相关性分析

车流密度、行车速度和交通流量是反映交通流特征的基本参数，随着流量的增加，车道内的车流密度加大，车头间距减小，行车速度开始受到车流密度的约束，而当车流密度增加时，速度降低且流量增加缓慢，密度进一步增加时速度继续下降且流量也随之下降，因此在交通流预测模型中，考虑参数间相关性对预测模型精度的提高至关重要。

与交通流时空相关性结合分析，横向截面空间中，车道间流量速度相互影响，时间段中，1月内，每周间的流量和速度具有相似性；1周内，每日的流量和速度存在规律性变化，工作日(周一至周五)早高峰7：00—9：00和晚高峰18：00—20：00速度会出现下降，而流量会出现上升，没有重大特殊事件的情况下，休息日(周六、周日)不会出现明显的波峰波谷现象；1日内，不同时间段的交通流状态变化较大，与前后时间片存在明显相关性，会对后一时间片的交通流产生影响。

2 短时预测模型构建

2.1 PCA主成分分析融合

在交通流预测研究方面，由于场景较为复杂，对同一研究对象存在大量的不确定性影响因素。虽然丰富的信息所包含的信息量较大，但模型训练和计算时长会相应增加。PCA是一种数学方法，利用线性变换将一组具有一定相关性的变量，重组成一组相互无关的变量，在保留原始信息的同时滤除相似信息。该方法在模式识别领域广泛用于图像融合处理[14]，对复杂数据进行降维。在交通领域中，无论是参数相关性还是时空维度数据组织，均需要准确而低复杂度的数据描述，PCA通过对车道的速度和流量进行线性变换，筛选出参数间的主要特征，实现对提取特征的精确表达，由于其本身具有降维作用，可降低时空数据的复杂度。

假设有n条样本数据，将其组成矩阵A:

(1)

将A的每一行进行零均值化：

(2)

式中，μ，σ为所有样本数据在特征维度上的均值和方差；a*为零均值标准化后的样本数据。

当数据投影到新向量上的位置越分散越能保留更多的信息，因此基向量正交时耦合程度最小，在不同基向量上的投影线性相关度的标准为协方差：

(3)

式中，m为车道数量；A为式(1)的矩阵，AT为转置矩阵。

不同特征之间协方差越小越好，于是将协方差C进行对角化，求出其特征值与对应的特征向量，对特征值进行排序，通过选取所需第1个特征值，将其对应的特征向量组织成向量组P，最后求解：

(4)

本研究采用PCA融合手段，进行特征提取，提取特征最大程度的保留了原有数据特性，以同一截面车道级数据为研究对象，通过微波数据，对强相关性的车道宏观参数进行特征级融合，在较大程度保留数据原有特性的同时，为交通决策分析提供可靠的依据。

2.2 GRU门控循环单元预测模型

循环神经网络因其同时具备前向反馈和后向反馈链路，能够应用于分析序列数据的上下文文本信息[15-16]和语音识别[17-18]等领域，而由于RNN(循环神经网络)存在梯度衰减或爆炸的现象，在实际应用中较难取得时间间隔较长的依赖关系，在2015年由Tian等[19]首次将LSTM(长短期记忆网络)模型运用到交通流预测领域，该模型在一定程度上解决了梯度爆炸问题，但模型训练时间较长，效率不高，而门控循环神经网络(Gated Recurrent Neural Network)的提出正好能解决这一问题。

GRU模型合并内部自循环Cell与隐藏层hidden，合并遗忘门、输入门为更新门，新增重置门rt，删除输出门，从而修改了RNN隐藏状态的计算方式，能有效缩短模型预测的时间。

门控循环单元中更新门和重置门的输入，均为当前时间步输入xt与上一时间步隐藏状态ht-1，输出由激活函数sigmoid通过全连接层计算得到。Wz和Wr分别是权重参数。

它的工作流程如下：

(1)更新门zt：决定前一时刻的状态对当前状态的影响。

zt=σ(Wz·[ht-1,xt])。

(5)

(2)重置门rt：决定对前一时刻状态的忽略程度。

rt=σ(Wr·[ht-1,xt])。

(6)

(7)

(8)

当重置门中的元素值接近0则意味着丢弃上一时间步的隐藏状态，接近1则保留。通过候选隐藏状态函数可以看出，重置门控制了上一时间步的隐藏状态从而更新当前时间步的候选隐藏状态，因此可以用来丢弃与预测无关的历史信息。而更新门可以控制隐藏状态如何被当前的候选隐藏状态更新，可捕捉时间序列中较长时间依赖关系。

本研究提出PCA-stacked-GRU模型，利用PCA建立横向相关性时空维度数据表达，提取宏观参数间的相关性特征，通过stacked-GRU实现基于横向车道级空间相关性及宏观参数相关性的短时交通流预测。

图2选取全天相关性最强的两条车道作为研究对象，其中该路段车道的数据组织，行按照时间片，列按照横向车道级参数形成时空维度矩阵，通过PCA将其处理成特征级融合向量，将该向量与两类不同的宏观参数组合，形成两个低维度的子矩阵1和子矩阵2，把这两类子矩阵作为stacked-GRU的输入(即为xt)，以实现交通流的预测。

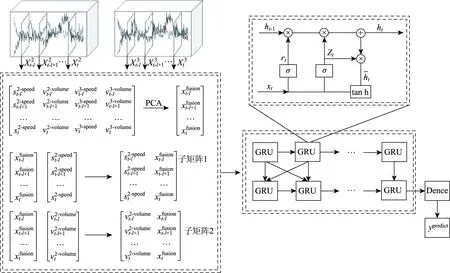
图2 PCA-stacked-GRU预测模型框架Fig.2 PCA-stacked-GRU prediction model frame

3 试验分析

本研究试验分析的道路结构，出于多方面考量和实际因素，选用合肥市天智路交叉口数据为研究对象，该数据集来源于微波检测器和视频检测器采集数据，因夜晚车流量较小，使数据离群值增大且影响模型性能，所以预处理阶段，需剔除夜晚22：00至清晨5:00的数据。

微波数据集采用2016年7月11日—7月17日，视频数据集采用6月22日—7月10日的交通流量数据和速度数据进行模型验证，为降低数据误差，将时间序列划成5 min为一个时间单位，按照时间片重新组织流量和速度，得到一天的数据量为192组，对缺失值采用同一天的上下时间片均值进行填充，形成模型可用数据集。

由于交通流量和速度具有时空相关性，对如图3所示天智路交叉口黄山路西进口的5个车道进行分析，通过相关性系数得到不同车道间交通流参数的相关性影响，试验可知，相关系数大于0.8的强相关车道为2号车道与3号车道。故本研究以横向空间为2号和3号的车道数据为研究对象。

图3 天智路-黄山路交叉口拓扑图Fig.3 Topology of Tianzhi Road and Huangshan Road intersection

将检测器DETECT_ID(检测设备编号)和ROAD_ID(车道编号)对应到相应的车道，并将速度整合为1个时间片内的平均速度，流量为1个时间片内的总流量，表1为预处理后2号，3号车道微波检测器断面数据集。

分别将表1，表2中的2号和3号车道的流量、速度采用PCA进行数据融合，通过线性变换提取速度-流量相关性特征，并将其表示为只有1列的融合向量组。

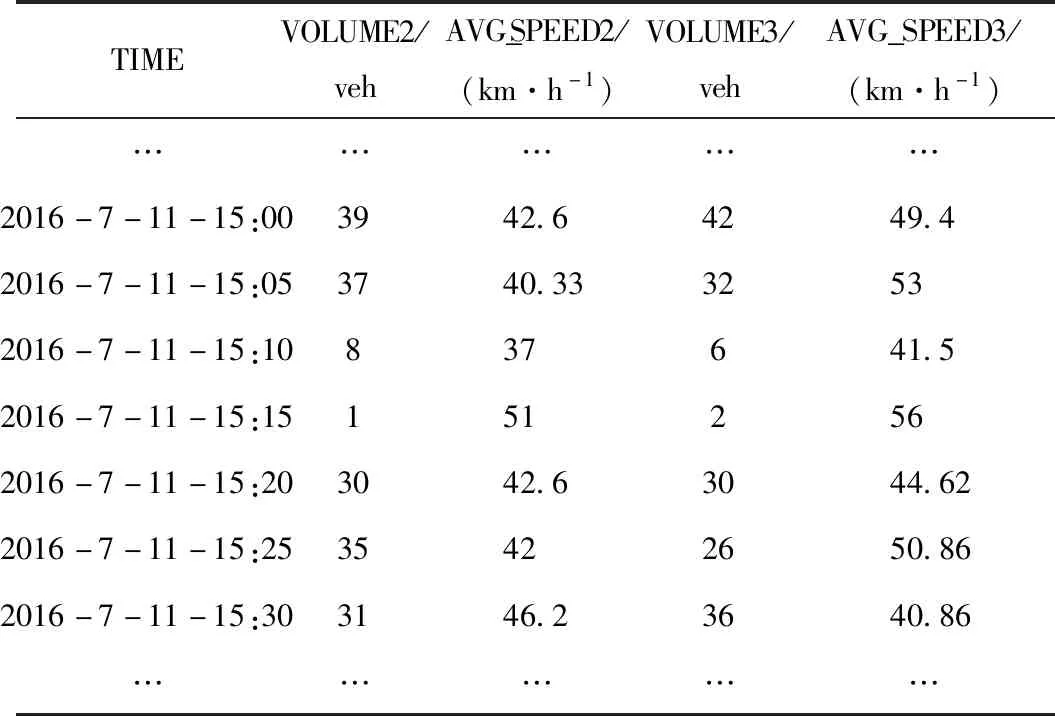
表1 微波检测器部分数据Tab.1 Partial data of microwave detector

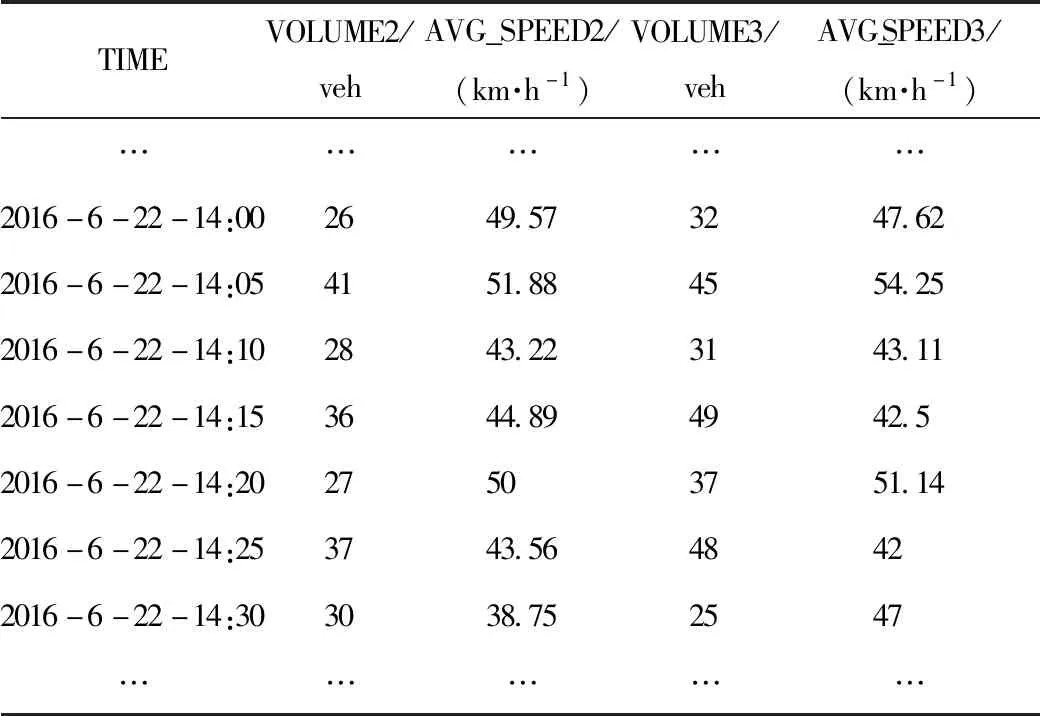
表2 视频检测器部分数据Tab.2 Partial data of video detector

本研究的预测目标为某一车道的流量和速度，历史数据均以连续12个时间片为样本，用以预测下一时段的流量和速度，预测目标可用式(9)～式(14)表示：

V1=

(9)

V2=

(10)

(11)

S1=

(12)

S2=

(13)

(14)

评价指标采用MAPE，MAE，MSE和RMSE来衡量预测精度。

(15)

(16)

(17)

(18)

3.1 微波数据集的流量与速度预测结果

基于对微波采集交通数据(2016-7-11—2016-7-20)进行的试验分析和评估，训练集为2016-7-11—2016-7-17，测试集为2016-7-18—2016-7-20，图4与图5为微波数据在不同模型中的单日预测结果图。

图4 2号车道微波流量预测图Fig.4 Curves of predicted microwave volume in Lane 2

图5 2号车道微波速度预测图Fig.5 Curves of predicted microwave speed in Lane 2

在微波数据集中可以看出，早高峰和晚高峰流量的显著上升，相应时间段速度的下降，满足交通流的时间特性，从空间特性来看，使用考虑参数相关性和横向车道级空间相关性的PCA-stacked-GRU模型对速度和流量进行预测，其预测值相较于其余模型的平均相对误差最小，考虑参数相关性的PCA单车道模型的预测精度优于未考虑参数相关性的单车道模型，证明考虑参数相关性和横向车道级相关性的预测方法能更加有效地估计未来交通运行状态。

通过表3和表4可知，单车道流量、速度预测最优的平均绝对误差分别为5.172 260和3.183 893，PCA单车道流量、速度预测误差均明显小于单车道，分别为5.116 309 1和3.133 064，而PCA双车道流量、速度预测误差优于PCA单车道，分别为4.946 960和3.109 925；通过其余指标对比同样可以看出PCA双车道预测精度高于PCA单车道预测高于单车道预测。

表3 微波数据集单双车道不同模型预测流量误差Tab.3 Predicted volume errors of single lane and double lanes in microwave data set by different models

表4 微波数据集单双车道不同模型预测速度误差Tab.4 Predicted speed errors of single lane and double lanes in microwave data set by different models

因此可以证明，考虑横向车道级空间相关性和速度-流量参数相关性的预测结果优于仅考虑单一参数的短时交通预测结果。

3.2 视频数据集的流量与速度预测结果

基于对视频采集交通数据(2016-6-22至2016-07- 10)进行的试验分析和评估，训练集为2016-06-22至2016-07-06，测试集为2016-07-07至2016-07-10，图6与图7为视频数据在不同模型中的单日预测结果图。

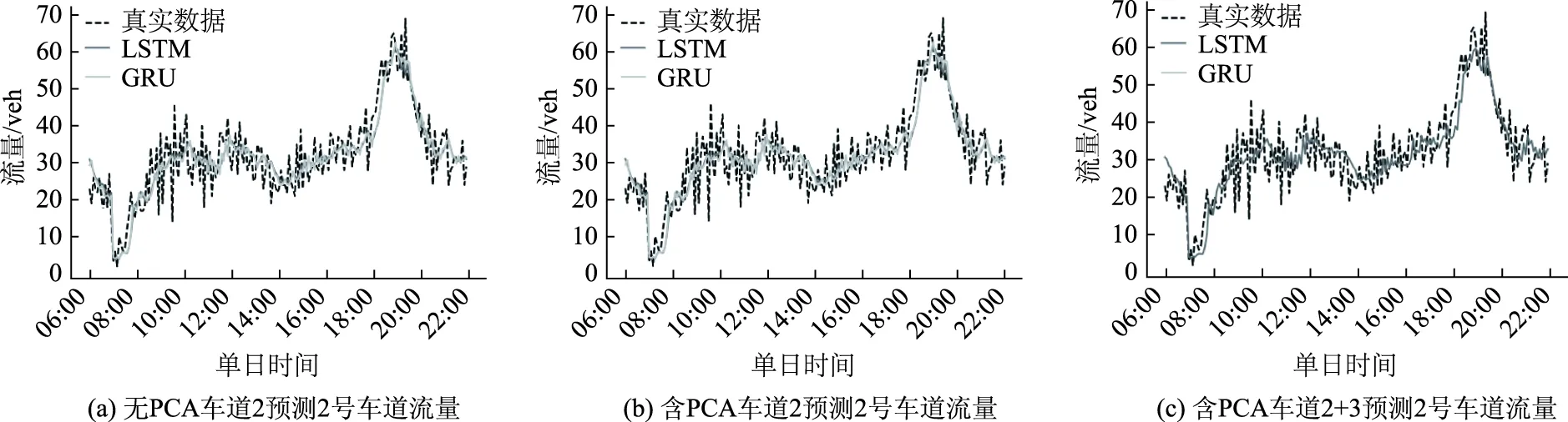
图6 2号车道视频流量预测图Fig.6 Curves of predicted video volume in Lane 2

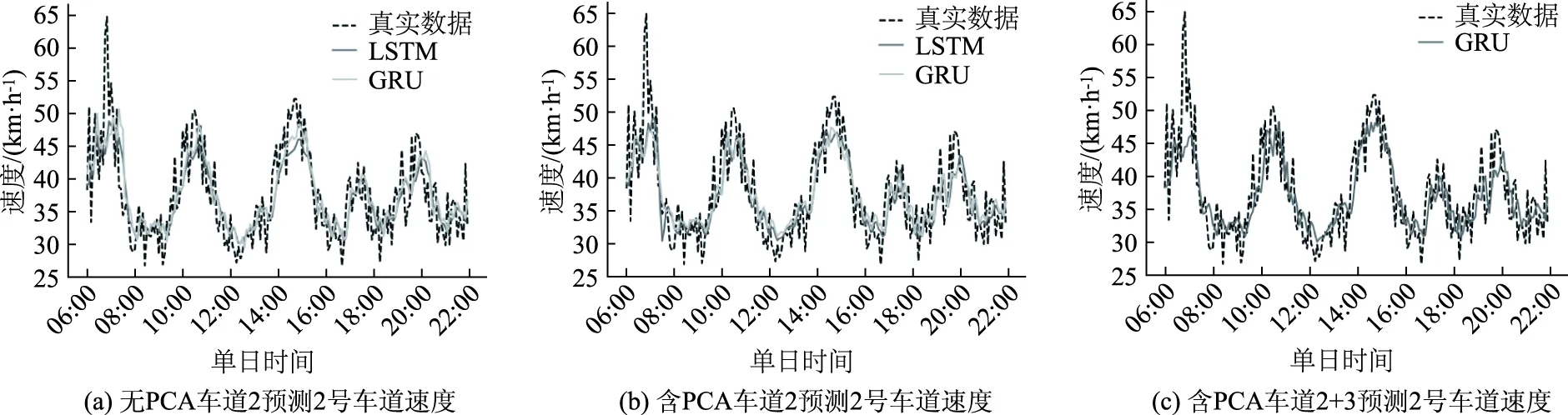
图7 2号车道视频速度预测图Fig.7 Curves of predicted video speed in Lane 2

通过表5和表6可知，单车道流量、速度预测的最优平均绝对误差分别为 4.503 461 和 3.863 718，而 PCA 单车道流量、速度预测误差均小于单车道，分别为 4.588 115 和 3.784 969；PCA 双车道流量、速度预测误差最小，分别为 4.489 486 和 3.712 197。通过其他几个指标对比也可以看出 PCA 双车道预测精度高于 PCA 单车道预测精度高于单车道预测精度。因此在视频数据集中同样可以证明，考虑横向车道级空间相关性和速度-流量相关性的预测结果优于仅考虑单一时间序列的短时交通预测序列。

表5 视频数据集单双车道不同模型预测流量误差Tab.5 Predicted volume errors of single lane and double lanes in video data set by different models

表6 视频数据集单双车道不同模型预测速度误差结果Tab.6 Predicted speed errors of single lane and double lanes in video data set by different models

由于充分考虑了空间相关性，综合运用了不同车道的参数信息，提高了预测样本的时空覆盖率，从而使预测结果相对于单一车道较好。同时，PCA-stacked-GRU模型在微波数据集和视频数据集中均表现优于其余模型，证明该模型具有鲁棒性。

综上所述，将本研究所提模型与其他常用基准线模型分析可知，本研究的PCA-stacked-GRU模型因其考虑了横向车道级空间相关性和速度-流量参数相关性，在预测精度上均优于其他未考虑相关影响因素的基准线模型，且具有鲁棒性。

4 结论

为提高预测模型的精度及在现实场景中的预测表现，本研究针对预测模型中横向相关性及宏观参数相关性考虑不足的问题，提出PCA-stacked-GRU组合预测模型，利用相关性系数选出强相关车道，对强相关车道的速度和流量进行特征级融合，得到考虑横向相关性及速度-流量相关性的数据表达；并通过stacked-GRU模型，在微波数据集和视频数据集上进行验证，与未考虑横向相关性及宏观参数相关性的常用基准线模型分析比较可知，本研究所提模型在MAPE，MAE，MSE和RMSE这4个误差指标上均优于其他模型。试验结果证明了考虑横向车道级空间相关性和速度-流量参数相关性的模型，在预测现实场景中的速度和流量时更加精确。未来研究中，可结合多源数据融合提高数据精度，通过对多位置传感器数据的运用，将空间因素对交通流预测的影响考虑的更为全面，从而进一步提高模型的预测性能。