基于并联管道的流量检测试验研究*

2022-06-17林祖根卿兆波

中国安全生产科学技术 2022年5期

林祖根，贾波，卿兆波，李青

(1.中国计量大学机电工程学院，浙江杭州 310018；2.浙江省应急管理科学研究院，浙江杭州 310020)

0 引言

在粉尘排放管道内流体及环境参数监测系统中，流量是反应管道状况最基本，也是最重要的指标。到目前为止，已经有多种技术被用于测量流量[1]。主要分为侵入式测量技术和非侵入式测量技术。文献[2]采用流体力学落差法并利用皮托管测量风道上2个断面的差压值，通过伯努利方程和连续方程计算得到通风机的排风量；文献[3]基于3D数值模型,并对巷道内平均风速的分布规律进行了数值分析，验证了单点测风法的可行性；文献[4-5]采用LDA激光多普勒测速仪反映巷道流场风流湍流脉动特性；文献[6]利用Fluent仿真技术对巷道流动进行仿真分析，并通过试验验证仿真结果和误差补偿方程令测量结果更加准确。

然而，传统的侵入式测量仪器局限性较大，当管道内部需要清理或者检修的时候，拆卸过程中容易造成传感位置的偏差，使测量准确度下降，而非侵入式的测量仪器对管道内部流体的流动状态要求较高，且价格相对昂贵，在工业生产中应用极少。

综上，本文基于现有的管道平台，自主搭建1套全新的风速检测结构，并且针对该结构研究出1种建模方法，提高对风量监测的精度和可靠性。

1 试验基本原理

系统通过添加分管的方法来实现对主管道内流量的测量。具体设计方法是通过改装现有管道平台的一段直管道，在主管上引出分管，变成并联管道的形式，如图1所示。

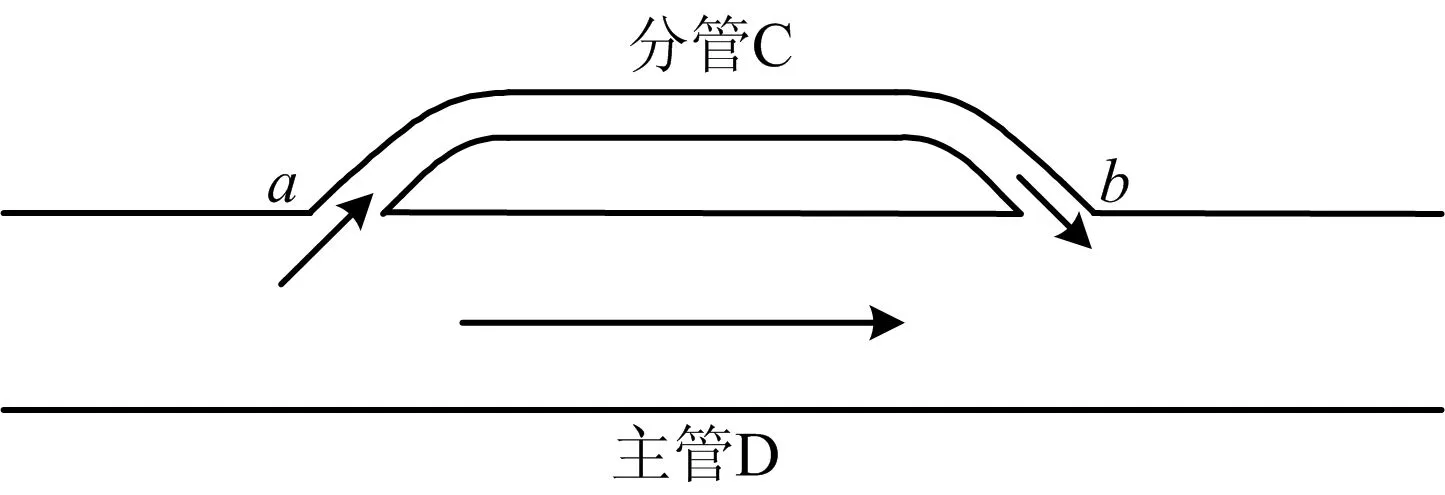
图1 并联管道内流体流动示意Fig.1 Schematic diagram of fluid flow in parallel pipeline

对于不可压缩流体，图1中的并联管道具有以下特点[7]：

1)总管流量是各支管流量之和，如式(1)所示：

Qi=QC+QD

(1)

式中：Qi表示管道内总流量，m3/s；QC为支管C的流量，m3/s；QD为支管D的流量，m3/s。

2)并联管路2节点间流动阻力损失相等，如式(2)所示：

hFi=hFC=hFD

(2)

式中：hFi为节点a,b间的流动阻力损失，J/kg；hFC为支管C内的流动阻力损失，J/kg；hFD为支管D内的流动阻力损失，J/kg。

对于并联管道的流量计算[8]，如式(3)所示：

(3)

式中：λ为管壁摩擦阻力系数；ζ为局部阻力损失系数；L为管道长度，m；d为管道直径，m；u为管道截面流速，m/s。g为重力加速度,m·s-2

又根据速度计算式，如式(4)所示：

(4)

得如式(5)所示：

(5)

因此，对于图1中各支管流量比则如式(6)所示：

(6)

式中，当管道的形状确定后，可认定dC、dD、LC、LD、ζC、ζD为恒定值。那么QC，QD的比值仅与λC，λD有关。由莫迪图可知，λ与管壁绝对粗糙度Δ、管道直径d、雷诺数Re值有关，又因为Δ与d在流体流动过程中保持不变，则λ仅随Re值而改变，而Re作为可以表征流体情况的无量纲数，在一定程度上可以反映管道内流体的平均流速，而静压值是指流体在静止或者匀速直线运动时表面所受的压强的大小，当分管内平均风速值发生变化时，静压值也会发生相应的变化，因此，由以上推理可知，静压值与管道内的流量具有一定相关性，那么利用分管内的静压值去反映主管内流量值是可行的。

2 试验结构设计与测量方法

2.1 试验装置

图2表示的为对管道进行改装并进行相关参数测量的试验装置原理图。图中D表示主管内径。

图2 试验装置原理Fig.2 Schematic diagram of experimental device

试验平台中用于被改装的直管道长为2 000 mm，直径300 mm，管壁厚10 mm，材料为有机玻璃。同时为使分管中的气流发展的更加平稳且数据更方便采集，选择在距离管道气流入口500 mm处，切割出改装分管的入风口，分管直管道和弯管的水平总长约为1 000 mm，其中分管直管部分长586 mm，直径71 mm，壁厚2 mm。考虑流动阻力损失，分管弯管部分采用45°弯管。其中，各部分之间的连接处均由聚合物粘合剂进行粘合处理。

对于主管中测量截面的选取，原则上应选择在气流平稳的直管段上。而当测量断面设在弯头、三通等异形部件时(相对气流流动方向)，距这些部件的距离应大于2倍管道直径。当测量断面设在上述部件后面时，距这些部件的距离应大于4～5倍直径。当测试现场难以满足要求时，为减少误差可适当增加测点。同时需确保测量断面位置距异形部件的最小距离至少是管道直径的1.5倍[9]。因此，根据改装好后的实际管道装置结构，选择在距离风流入口4.5倍直径处作为分管和主管数据测量截面。并利用皮托管和差压传感器采集静压值，其中皮托管利用粘合剂固定于分管上，并调节位置令静压感应口处于分管中心轴上且平行于来流方向。利用热膜风速传感器采集主管内的风速值，并利用法兰固定，最终由处理器将相关数据发送至上位机监测平台并对数据进一步处理。实际装置图如图3所示。

图3 试验装置实物Fig.3 Physical drawing of experimental device

2.2 测点布置

为准确测量断面风速分布，必需布置合理的风速测点。通常采用等环面积法模型将圆断面分成若干个等面积环。等面积环数越多，测点越多，则测试精度越高[10]。一般都按风筒直径大小确定等面积环数，可参考表1。

表1 圆形风管的分环数Table 1 Number of rings in circular wind pipeline

虽然试验所测管道通风直径为280 mm，但由于对管道进行了改装，使得无法从纵向上布置测点，且风流从入口处至测量截面处还处于未完全发展阶段，且从试验前期测得，风机电源供电频率(以下均简称频率)由5～35 Hz变化时，管道中心风速从2.35 m/s变化至11.05 m/s，且由雷诺数计算公式可知测风试验所处的流体运动状态恒为湍流流动，因此为了试验结果更加准确，试验中将圆形截面分成5个等面积环，布置20个测点，如图4所示。

图4 测点布置Fig.4 Layout of measuring points

各测点距离管道中心的距离Ri如式(7)所示：

(7)

各测点到管道壁的距离li如式(8)所示：

(8)

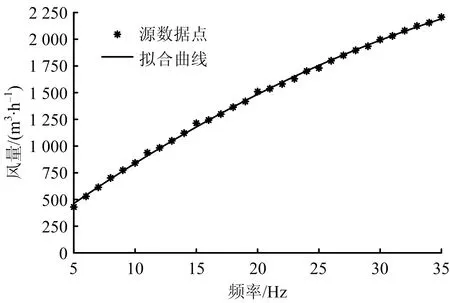
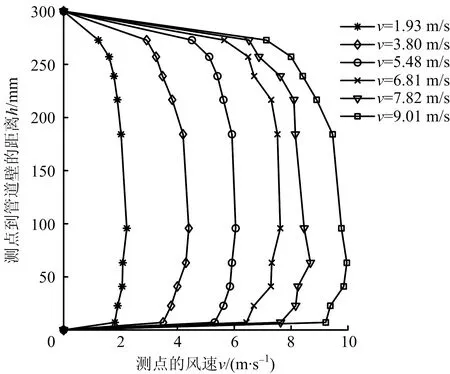
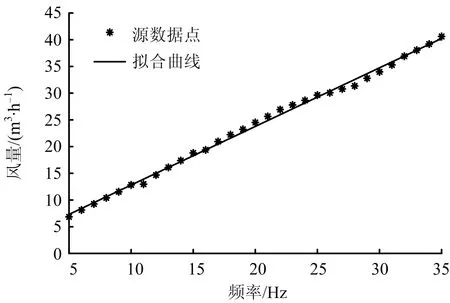
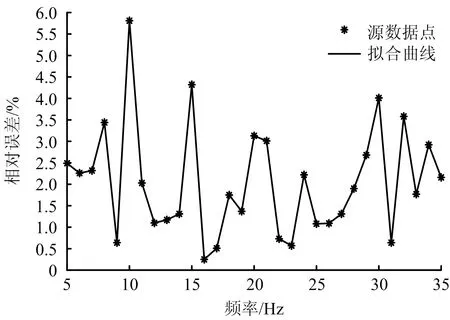
式中：i为从管道中心算起的等面积环编号数；n为等面积环数；D为管道断面直径，mm；R为管道断面半径，mm；li为i环中心至壁面的距离，mm(其中li>R时取“+”号，li

根据式(8)计算出各风速测点到管道壁的距离如表2。

表2 各风速测点到管道壁距离Table 2 Distance from each measuring point of wind speed to pipeline wall

因此，当布置好测点，并测得相应测点上的风速后，通过管道的截面积便可以计算得知流过管道截面的风量大小。在本文中风量大小按小时进行计算，单位为m3/h，风量计算公式如式(9)所示：

(9)

式中：qv为截面风量大小，m3/h；n为测点数量；vi为各测点局部流速，m/s；A为管道截面面积，m2。

3 数据采集与分析

3.1 数据采集

本文所使用的电机为离心风机，通过变频器改变风机电源供电频率来实现调速，因此当启动风机开始试验后，逐渐调节频率由5～35 Hz，并对每一频率下的截面上每个测点采集的样本速度进行平均化处理，即将试验中对某一测点在不同时刻测得的速度转化成测点的平均速度[11]。则式(9)中vi的转换式如式(10)所示：

(10)

式中：vi为测点局部流速，m/s；vk为截面上某一测点的样本例子速度，m/s。

在本文试验中m值取15，且选择每隔1秒采集1个数据。则每调节1次频率，需要测量主管圆形截面上，共计20个测点，300个测点风速的数据，那么在同时也采集了300个分管静压数据，静压值数据处理公式如式(11)所示：

(11)

式中：Pd为平均静压值，Pa；Pdj为分管中测得的某一时刻的样本例子静压值，Pa。

3.2 数据拟合与分析

利用Matlab软件对测量数据进行分析，得到各不同频率与主管内风量和分管内静压之间的关系，图5所示为频率与主管内风量曲线关系图，该曲线关系通过二次函数关系式进行拟合，拟合公式如式(12)所示：

图5 频率与主管风量曲线关系Fig.5 Curve relationship between frequency and air volume of main pipeline

y=-0.76x2+87.82x+32.25

(12)

式中：x表示频率值大小，Hz；y表示风量值大小，m3/h。

图6所示为频率与分管内静压曲线关系图，该曲线通过二次函数进行拟合，拟合公式如式(13)所示：

图6 频率与静压曲线关系Fig.6 Curve relationship between frequency and static pressure

y=0.063 04x2+0.228 4x+0.235

(13)

式中：x表示频率值大小，Hz；y表示静压值大小，Pa。

由图5可知，对于在改装后的管道平台进行测量时，频率由5～35 Hz变化过程中，随着频率升高，测量并处理得到的主管风量值也相应增加。同时，通过图6可知，分管内的静压值同样随着频率的上升而增加，这是由于随着频率的上升，分管内的平均风速值也随之升高，因此使得静压值也随之上升。同时，观察上述2条曲线可知，它们的上升符合基本规律，且上升趋势较为平缓，因此便可对风量值和静压值进行拟合，以此便可以通过分管内的静压值来反映主管内的风量，图7所示为分管静压值与主管内风量曲线关系图，二者利用幂函数关系式进行拟合，拟合公式如式(14)所示：

图7 静压与风量曲线关系Fig.7 Curve relationship between static pressure and air volume

y=932.4x0.264 6-813.8

(14)

式中：x表示静压值大小，Hz；y表示风量值大小，m3/h。

由拟合后的曲线所示，在圆管和湍流非充分发展情况下，风量值与静压值呈正相关分布。此外，不同的静压值下所对应的风量值的源数据点，与拟合曲线重合度高，说明了拟合效果较为良好。进一步地，根据曲线的整体变化趋势来看，在静压值偏小时，曲线切向斜率较大，风量随静压变化相对明显；随着静压值增大，曲线切向斜率逐渐减小，风量值随静压上升增加更缓慢。综上，根据分管内的静压值去得到主管内的风量值是完全可行的。

表3所示为试验中部分频率下测得的分管内静压和主管内风量的相关数据。

表3 分管内静压与主管内风量数据表Table 3 In charge of internal static pressure and in charge of internal air volume data table

3.3 截面风速分布趋势说明

同时，为了解改装好后主管内截面风速的分布趋势，并以此作为一个判断改装管道后风量计算的可靠性验证。对测试结果利用Matlab软件作进一步的数据分析处理，得到风机供电频率分别为5，10，15，20，25，30 Hz时测量截面上左、右45°线上各测点的速度分布趋势图，分别如图8和图9所示。在以上这些频率下，通过风量并计算得到的主管内平均风速为1.93，3.80，5.48，6.81，7.82，9.01 m/s，从左、右45°线上各测点速度分布的趋势图可知，在平均风速相对不大时，靠近上方管道壁处速度较小，中心区域速度较大，同时靠近下方管道壁处速度小于中心风速，但略大于靠近管道壁上方风速；而随着平均风速的增加，左、右45°线上风速呈现多样化分布的特征，整体上来看，管道中下部的风速相对大于中上部的平均风速。同时，与平均风速较小时相比，在左、右45°线上，越靠近管道壁风速分布曲线更加陡峭，对该现象进一步分析可知，当平均风速增加，管道内湍流运动将更加显著，同时加上加装分管对风速分布的影响，因此使得测量断面上风速分布不稳定性上升。

图8 左45°线上速度分布趋势Fig.8 Velocity distribution trend on left 45° line

图9 右45°线上速度分布趋势Fig.9 Velocity distribution trend on right 45° line

4 误差对比试验

为了解管道改装后和未改装前风量测量数值的相对误差，需要对改装前后同一频率下的管道内总风量进行测量对比，改装后管道的总风量由主管风量和分管风量组成，对于分管风量，采用手持式高精度UT362风速仪进行测量，安装位置与皮托管位置一致，如图10所示。同时利用式(10)进行风速的采集与处理，通过采集并处理后得到的平均风速值以及分管的截面积便可以得到分管的风量值。

图10 分管风量测量示意Fig.10 Schematic diagram of air volume measurement in branch pipeline

因此，通过试验测得相关数据，并利用Matlab处理得到改装后频率与分管风量的曲线关系图，如图11所示，该曲线利用线性函数进行拟合，拟合公式如式(15)所示：

图11 频率与分管风量曲线关系Fig.11 Curve relationship between frequency and air volume of branch pipeline

y=1.097x+1.831

(15)

式中：x表示频率值大小，Hz；y表示风量值大小，m3/h。

对于改装前主管风量的测量方法与改装后相同，并已于改装前测得。同样地，利用Matlab对所测数据进行处理得到改装前频率与主管风量的曲线关系图。如图12所示，该曲线利用二次函数进行拟合，拟合公式如式(16)所示：

图12 频率与改装前主管风量曲线关系Fig.12 Curve relationship between frequency and air volume of main pipeline before modification

y=-0.699 7x2+85.59x+52.47

(16)

式中：x表示频率值大小，Hz；y表示风量值大小，m3/h。

同时计算改装前后总风量相对误差，如式(17)所示：

(17)

式中：A为真实值，记为改装前的管内总风量，m3/h；a为测量值，记为改装后主管风量和分管风量之和，m3/h。便可以得到图13所示的改装前后管内总风量相对误差对比图。

图13 改装前后管内风量相对误差对比Fig.13 Comparison on relative error of air volume in pipeline before and after modification

根据误差对比试验来看，改装前后测量计算得到的总风量相对误差值最大为5.81%，最小为0.51%，平均相对误差为2.05%，以上数据说明改装管道会带来一定的测量误差，但这一误差对于本平台中管内流动为非充分发展的湍流来说，这个误差是在允许范围的。表4所示为试验中部分频率下测得的改装前后管道内总风量的相关数据对比。