一类线性差分方程的最优Ulam常数
2022-06-17侯牧林
侯牧林, 徐 冰
(四川大学数学学院, 成都 610064)
1 引 言
1940年,Ulam最早提出了函数方程的稳定性问题,即在方程近似解的附近是否存在真解. 1941年, Hyers关于Cauchy方程
f(x+y)=f(x)+f(y)
的稳定性研究给出了肯定回答[1]. 正因如此,后来的研究者们多将函数方程的此类稳定性称为Hyers-Ulam稳定性或Ulam稳定性. 当前,关于各类函数方程的Ulam稳定性,已有不少研究成果[1-7].
在函数方程的Ulam稳定性基础上,人们希望进一步刻画近似解与真解的接近程度,进而产生了最优Ulam常数的概念[6]. 例如,对于一类重要的函数方程
xn+p=a1xn+p-1+…+apxn
(1)
人们对其Ulam稳定性和最优Ulam常数展开了深入研究.我们有如下的定义:
定义1.1[5]若对于任意给定的ε>0和满足
‖yn+p-a1yn+p-1-…-apyn‖≤ε,n∈N
的序列{yn}n∈N,都存在常数K>0和满足方程(1)的序列{xn}n∈N,使得 ‖xn-yn‖≤Kε, 则称方程(1)为Ulam稳定的,并称常数K为方程的Ulam常数.
显然,若K0>K,则K0也是方程(1)的Ulam常数.记K为方程(1)的所有Ulam常数构成的集合.我们有如下的定义:
定义1.2[2]设K*=infK.若K*是方程(1)的Ulam常数,则称K*为方程(1)的最优Ulam常数.
Brzdek等证明:当且仅当方程(1)的所有特征根的模不等于1时,方程(1)具有Ulam稳定性[4]. 随后,针对所有特征根的模大于1的情形, Baias等首先给出了当p≤3时方程(1)的最优Ulam常数[3],之后又对一般的p给出了当所有特征根均为单根时方程(1)的最优Ulam常数[2].
本文对一般的p继续研究方程(1)的最优Ulam常数问题. 在方程(1)有且只有一个特征根r的条件下,我们首先使用常数变易法给出该方程的通解,进而在|r|>1的条件下构造了该方程的一个特别有界近似解,最终给出方程的最优Ulam常数.
2 预备知识
设N为非负整数集,K为数域R或C. (X,‖·‖)为数域上的Banach空间.本文考虑Banach空间X上的p阶线性差分方程
xn+p=a1xn+p-1+…+apxn
(2)
其中a1,…,ap∈,x0,…,xp-1∈X.下面的定理给出了方程(2)具有Ulam稳定性的充分条件.
定理2.1[4]设λk为方程(2)的特征方程
λp=a1λp-1+a2λp-2+…+ap
的特征根,k=1,2,...,p.若|λk|≠1,则对任意给定的ε>0及X中满足条件
‖yn+p-a1yn+p-1-…-apyn‖≤ε
的序列{yn}n∈N,均存在X中满足方程(2)的序列{xn}n∈N,使得
3 主要结果
为简便起见,本文补充定义
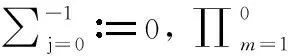
引理3.1设p≥2.定义

Wk(n+1)为行列式W(n+1)中第p行第k列的代数余子式,k=1,...,p.则有以下结论:

(iii)Wk(n+1)=
其中k=1,...,p.
证明 (i) 显然有W(n+1)为p阶范德蒙行列式,从而

由W1(n+1)的定义可知,
从而
故结论(i)成立.
(ii) 考虑辅助函数

(3)
式(3)右端的行列式也是范德蒙行列式,从而有
由Wk(n+1)定义可知,Wk(n+1)也为式(3)右端行列式中第p行第k列的代数余子式.因此,按式(3)右端行列式的最后一行展开得

(4)
(iii) 由式(4)可知,Wk(n+1)为多项式函数gn(x)中x的第k-1次项的系数.由多项式乘法原理易推知结论(iii)成立. 证毕.
引理3.2设p≥1,n∈N.若r为方程(2)的特征方程
λp=a1λp-1+a2λp-2+…+ap
的p重根,则方程
yn+p=a1yn+p-1+…+apyn+bn
(5)
的通解为
其中{bn}n∈N为X中的序列,C1,…,Cp为X中的任意常数.
证明 当K=C时,X为复Banach空间.此时我们有r∈K.当K=R时,X为实Banach空间.由实系数多项式方程的性质可知,此时一定有r∈R,从而有r∈K.
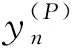
(6)
其中
(7)

(8)
其中C1(n),C2(n),...,Cp(n)为待定系数.令
ΔCk(n)=Ck(n+1)-Ck(n),k=1,...,p.

rn+1C1(n+1)=rn+1C1(n)+bn,
从而有

此时方程(5)的通解为
(9)
当p≥2,n∈N时,由于rn,nrn,…,np-1rn是齐次方程(2)的一个基本解组, 因此一定可以选出一组C1(n),C2(n),…,Cp(n),使得
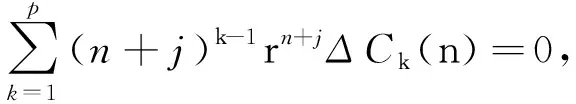
1≤j≤p-1
(10)
由式(8)和(10)可得
依此类推,易知
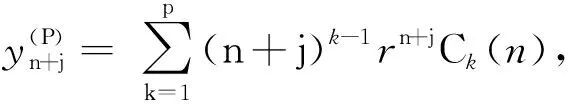
1≤j≤p-1
(11)
事实上,不妨假设当j=q时有
成立.则当j=q+1时, 有
由归纳法知式(11)成立.
特别地,在式(11)中,当j=p-1时有
因此
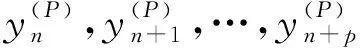
整理得
由于rn,nrn,…,np-1rn是齐次方程(2)的一个基本解组, 故对每个k=1,...,p都有
(12)
因此, 将式(12)代入上述等式化简可得
(13)
由式(10)和(13)可知, 待定系数C1(n),…,Cp(n)满足Casorati矩阵方程[7],即对每个n∈N都有
(14)
由克拉默法则可知, 对每个k=1,...,p,n∈N, 方程(14)存在唯一解
因此, 方程(5)的一个特解为
由引理3.1中的结论(i)和(ii)可得
(15)
由式(6)和(15)可知, 此时方程(5)的通解为
(16)

证毕.
定理3.3设p≥1,n∈N,r为方程(2)的特征方程
λp=a1λp-1+a2λp-2+…+ap
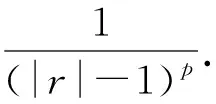
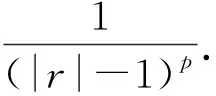

(17)
可知bn∈X,‖bn‖=ε.
当p=1时,由于|r|>1且‖bn‖=ε,可以定义X中的序列
其中
(18)
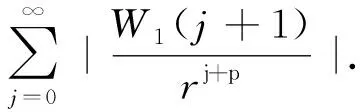
(p-1)k-1|W1(j+1)|.
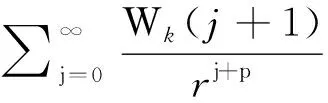
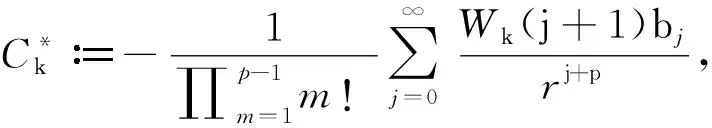
k=1,...,p.
定义X中的序列

(19)

为方程(5)的一个特解. 记s=j-n.则有
(20)
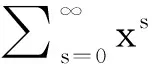
在(20)式两端同时关于x求p-1次导得
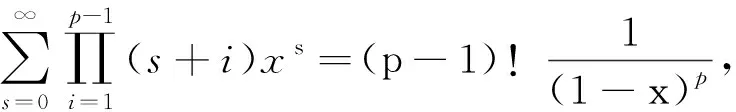
|x|<1.
由|r|>1有
(21)
再由式(20)和(21)得


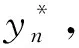
使得
(22)
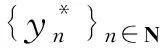
从而有

