对称式基坑渗流涌水量的计算方法

曹净++张丙军++刘海明

摘要：随着地铁、越江隧道等地下工程的日益增多，涌现出了大量的对称式基坑。基于共形映射理论，推导了对称式基坑涌水量计算表达式，并对其计算参数进行分析。研究表明，对称式基坑的单宽涌水量与渗透系数、基坑内外水头差成正比，与（相对）隔水层层顶到坑底的距离和基坑两侧止水帷幕间距的比值、止水帷幕嵌固深度和（相对）隔水层层顶到坑底距离的比值、基坑内外水头差和（相对）隔水层层顶到坑底距离的比值成反相关。

关键词：对称式基坑；共形映射；渗流；涌水量

中图分类号：TU46.3文献标志码：A文章编号：16744764（2017）01010606

收稿日期：20160712

基金项目：国家自然科学基金（51304088）

作者简介：曹净（1966），男，博士，教授，主要从事岩土工程研究，（Email） cjlb117@sina.com。

Received：20160712

Foundation item：National Natural Science Foundation of China （ No.51304088）

Author brief：Cao Jing （1966），PhD， Professor， main research interest： environmental geotechnical engineering，（Email） cjlb117@sina.com.Calculation Method of seepage discharge for symmetric foundation pits

Cao Jing1，Zhang Bingjun1，2 ，Liu Haiming1

（1. Faculty of Civil Engineering and Mechanics， Kunming University of Science and Technology， Kunming 650500，

P. R. China； 2.Weifang Architectural Design & Research Institute Co.， LTD. Weifang 261041， Shandong， P. R. China）

Abstract：In recent years， with the development of crossingriver tunnels and subways， there are more and more symmetric foundation pits. Based on conformal mapping， the mathematical modeling is built and the expression of seepage discharge in pensile curtain foundation pit is deduced， then calculation parameters of seepage discharge are analyzed. The results showed that the seepage discharge of symmetric foundation pit has direct ratio with permeability coefficient and the water head between the outside and inside of foundation pit. And the seepage discharge of symmetric foundation pit is in inverse correlation to the ratio of the distance between the top of relative impermeable layer to the bottom of foundation pit and the distance between pensile curtains， to the ratio of the embedded depth of pensile curtain and the distance between the top of relative impermeable layer to the bottom of foundation pit， and to the ratio of water head between the outside and inside of foundation pit and the distance between the top of relative impermeable layer to the bottom of foundation pit.

Keywords：symmetric foundation pit； conformal mapping； seepage； discharge

随着中国城市基础建设的快速发展，地下空间的开发利用正成为各大城市的新热点，随之涌现出大量的深基坑。在基坑施工过程中常常因地下水的存在会引起一系列的问题，其中基坑的涌水量成为基坑降水设计和施工过程中所要重点考虑的问题。当基坑工程地质条件、水文地质条件变化不大或宽度较小时，可近似地认为基坑两侧采取的止水帷幕、基坑内外地下水位、基坑渗流区土层厚度及渗透系数成纵向对称，本文针对此类对稱式基坑进行涌水量计算和渗流分析。

共形映射又称保角映射，是复变函数的一个重要分支，广泛应用于流体力学[15]、复合材料断裂[68]、隧道围岩应力变形[911]、电磁场理论[1214]。本文利用共形映射将有止水帷幕的对称式基坑渗流平面转化为带状区域，推导其单宽涌水量的计算表达式，并对对称式基坑渗流单宽涌水量计算参数进行分析。

1解析解推导

在城市基坑降水施工过程中，为保证基坑周边已有建构筑物、设施、管线的正常使用，《建筑基坑工程检测技术规范》要求基坑坑外地下水位变化累计值不超过1 000 mm，变化速率不超过500 mm/d。故假定基坑坑外地下水位保持不变，如图1所示。

图1对称式基坑渗流示意图

Fig.1 schematic diagram of seepage field

in symmetric foundation pits图1为对称式基坑示意图，为了简化计算，假定渗流区土层为均质、各向同性，地下水运动符合达西定律，基坑开挖深度为H，基坑坑外地下水位与地面齐平，坑内水位降到坑底，即H也为基坑内外水头差，图中边agfg′a′为隔水边界或相对隔水边界，止水帷幕嵌固深度为h，渗流区土层厚度为T，基坑两侧止水帷幕间距为2S，则S为基坑两侧止水帷幕间距的一半。

止水帷幕厚度相对于基坑开挖深度、嵌固深度等可以忽略不计，含水层为双连通区域，可沿虚线nn′将基坑渗流区划分为两对称区域，且虚线为一条流线，因而可利用图1中的左边平面进行基坑渗流求解。

对图1的左侧平面的单连通区域（如图2所示）进行分析。对称式基坑渗流问题的解析解可以表达为w（z）=φ（x，y）+iψ（x，y），（z=x+iy）（1）式中：w为复势平面；φ为势函数；ψ为流函数；z为复数变量。

图2z平面渗流区示意图

Fig.2z plane schematic diagram of

seepage field in symmetric foundation pits 在ab边界上，φ=-kH；

沿agfe邊界上，ψ=q；

沿bcd边界上，ψ=0；

在de边界上，φ=0。

为了将图2中的z平面映射到图3中的t平面，由施瓦兹克里斯托费尔映射公式可得z=S-iP∫t0x-βx+αdxx（x-ε）（x-1）（2）式中：α>0；0<ε<1<β；P>0。

图3t平面中的渗流区

Fig.3seepage field in t planef→e：T-HP=∫κ20β-tt+αdtt（ε-t）（1-t）（3a）e→d：SP=∫1κ2β-tt+αdtt（t-ε）（1-t）（3b）d→c：hP=∫β1β-tt+αdtt（t-ε）（t-1）（3c）c→b：H+hP=∫∞βt-βt+αdtt（t-ε）（t-1）（3d）令：ε=κ2，得： κ′=1-κ2（4）式中：κ为模数；κ′为补模数。

根据文[15]可得T-H2P=1+βα∏0-κ2α，κ-K（κ）（5a）

S2P=α+β1+αΠ0κ′2α+1，κ′-K（κ′） （5b）

h2P=β-κ2α+κ2Fβ-1β-κ2，κ-

κ′2（α+β）（α+κ2）（α+1）Πβ-1β-κ2，α+κ21+α，κ（5c）

H+h2P=1+βαΠ1β，-α，κ-

βαF1β，κ（5d）式中：F（z，κ）=∫z0dx（1-x2）（1-κ2x2）为第一类非完全椭圆积分；K（κ）=F（1，κ）为第一类完全椭圆积分；κ为模数；Π（z，n，κ）=∫z0dx（1+nx2）（1-x2）（1-κ2x2）为第三类非完全椭圆积分；Π0（n，κ）=Π0（1，n，κ）为第三类完全椭圆积分。简化式（5），可得T-HS=1+βαΠ0-κ2α，κ-Kκα+β1+αΠ0κ′2α+1，κ′-K（κ′）（6a）

hT-H=β-κ2α+κ2Fβ-1β-κ2，κ1+βαΠ0-κ2α，κ-K（κ）

-κ′2（α+β）（α+κ2）（α+1）Πβ-1β-κ2，α+κ21+α，κ1+βαΠ0-κ2α，κ-K（κ）（6b）

H+hT-H=1+βαΠ1β，-α，κ1+βαΠ0-κ2α，κ-K（κ）-

βαF1β，κ1+βαΠ0-κ2α，κ-K（κ）（6c）求解等式（6），可求得参数α、κ、β的值。

为了使上方程组简化，令T1=T-H（7）式中：T1即为基坑（相对）隔水层层顶到坑底的距离。

下面将图2中的渗流区域映射到图4中，在ω平面中，ω=φ+iψ，参数ψc、ψf、ψg、q为未知变量，为了方便计算，用式（8）（辅助函数）进行变化。ω=ωqK（m′）-K（m）（8）式中：m为模数；0

K（m）=∫10dx（1-m2x2）（1-x2）（10）通过式（8）可将图4中的渗流区域映射到图5中。

图4ω平面中的渗流区

Fig.4seepage field in w plane图5ω平面中的渗流区

Fig.5seepage field in ω plane由图4和图5中b点对应关系可得K（m）=kHqK（m′）-K（m）（11）整理得q=12kHK（m′）K（m）（12）为了计算方便，将图5平面渗流区域共形映射到图6的上半平面。

图6ξ平面中的渗流区

Fig.6seepage field in ξ plane最终，可将问题简化为图3和图6之间共形映射关系的求解，由文[16]知，tξ之间的关系可通过a、b、d三点的对应关系进行确定，故关系式可以表达为t=A+B1-ξ（13）由点a、点d的对应关系得A+B1-1m=-α

A+B1-（-1）=1 （14）

t=2m+α（m-1）1+m+2（m-1）（α+1）（m+1）（ξ-1） （15）由点e在图3和图6中的对应关系，代入式（15）可得κ2=ε=2m+α（m-1）1+m+2（m-1）（α+1）（m+1）-1m-1（16）整理式（16）得（α+ε）m2+2（ε-α-2）m+ε+α=0（17）求解式（17）得m=α-ε+2-2（1-ε）（1+α）α+ε（18）通过m值，可用式（12）求解对称式基坑渗流的单宽涌水量。

前面公式推导过程知，计算对称式基坑渗流单宽涌水量的步骤为

1）先联立等式（6）三式，求得参数α、κ、β的值；

2）再利用式（18），求得m的值；

3）最后利用式（12）求得基坑的单宽涌水量。

通过式（6）、式（18）知，m值与T1S、hT1、HT1有关。

2影响参数分析

在上述模型中，影响对称式基坑单宽涌水量q计算的参数有：基坑内外水头差H、基坑（相对）隔水层层顶到坑底的距离与基坑两侧止水帷幕间距一半的比值T1S、止水帷幕嵌固深度与（相对）隔水层层顶到坑底距离的比值hT1 、基坑内外水头差H与（相对）隔水层层顶到坑底距离的比值HT1 以及渗流区土体的渗透系数k，本文仅对上述参数的影响进行分析。

图7对称式基坑示意图

Fig.7schematic diagram of seepage field2.1H的影响

当T1S、hT1 、HT1 、k一定时，由式（12）知：对称式基坑的单宽涌水量q与基坑内外水头差H成正比。

2.2T1S的影响

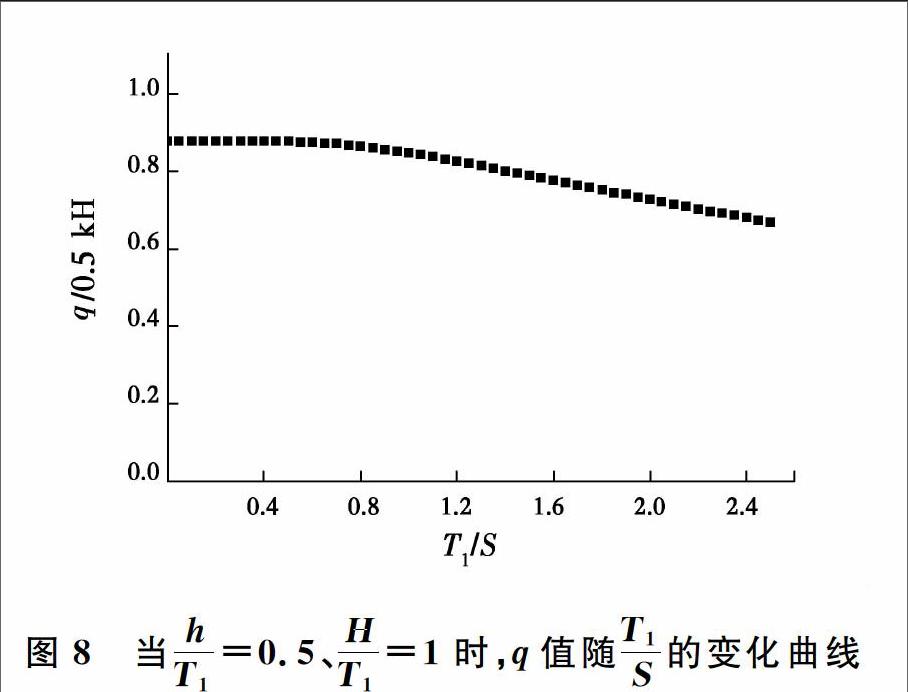
当hT1 、HT1 、k、H一定时，随T1S的增大，q先保持不变后减小，如图8所示。当T1S≤0.5时，q基本保持不变，T1S>0.5时，q大体呈线性降低。

图8当hT1=0.5、HT1=1时，q值随T1S的变化曲线

Fig.8The variation curve of q value with the change

of T1S when hT1=0.5 and HT1=12.3hT1 的影响

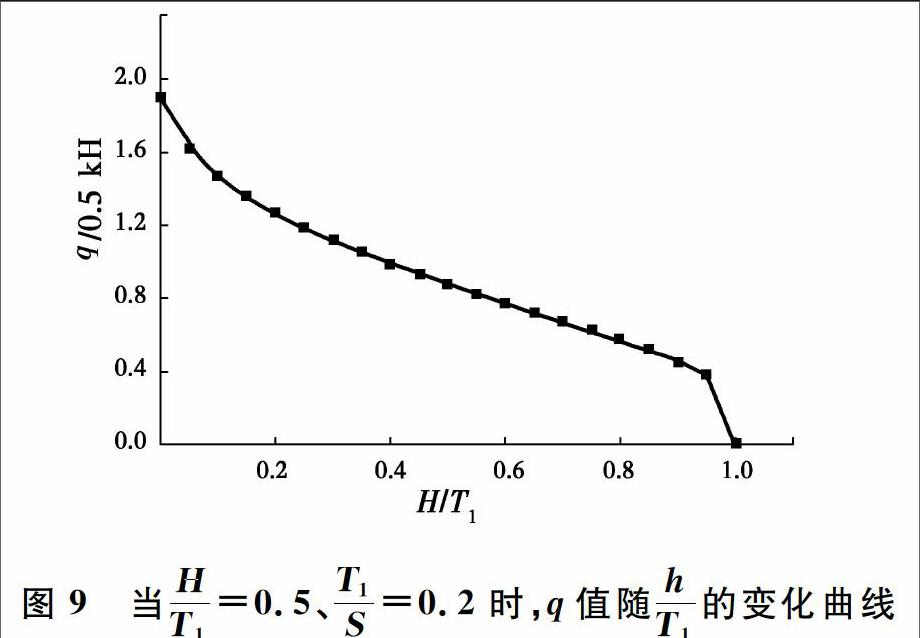
从图9可以看出，當T1S、HT1 、k、H一定时，随着hT1的不断增大，q逐渐减小，整体趋势呈先快后慢再快。值得注意的是，当hT1 = 1，即止水帷幕嵌固到（相对）隔水层中，对称式基坑的单宽涌水量q为零。

图9当HT1=0.5、T1S=0.2时，q值随hT1的变化曲线

Fig.9The variation curve of q value with the change

of hT1 when HT1=0.5 and T1S=0.22.4HT1 的影响

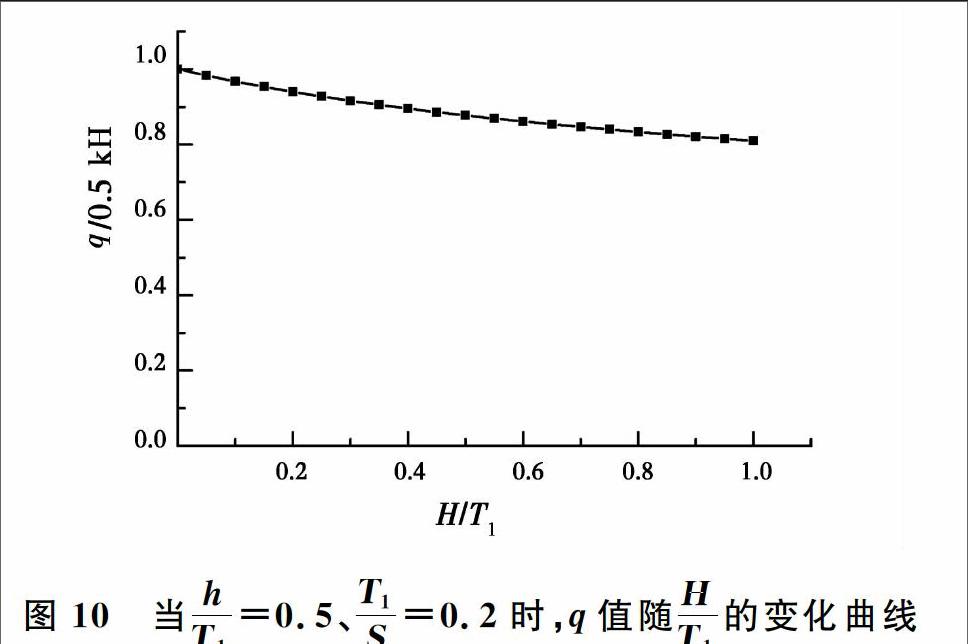
如图10所示，当hT1、T1S、k、H一定时，随着HT1 的不断增大，q逐渐减小，整体趋势呈先快后慢。

图10当hT1=0.5、T1S=0.2时，q值随HT1的变化曲线

Fig.10The variation curve of q value with the change

of HT1 when hT1=0.5 and T1S=0.22.5k的影响

由式（12）可知，对称式基坑的单宽涌水量q与基坑土体的渗透系数k成正比，不受H、T1S、hT1、HT1 的影响。

3结论

假定渗流区土层为均质、各向同性，且地下水运动符合达西定律，基于共形映射理论，推导了对称式基坑单宽涌水量的计算表达式，通过对其参数进行分析，可以得到以下结论：

1）当T1S、hT1 、HT1 、k一定时，对称式基坑的单宽涌水量q与基坑内外水头差H成正比。

2）当hT1 、HT1 、k、H一定时，随着T1S的增大，对称式基坑的单宽涌水量q先保持不变后减小。

3）当T1S、HT1 、k、H一定时，随着hT1的不断增大，对称式基坑的单宽涌水量q逐渐减小，整体趋势呈先快后慢再快。当hT1 = 1，即止水帷幕嵌固到（相对）隔水层中，对称式基坑的单宽涌水量q为零。

4）当T1S、hT1、k、H一定时，随着HT1 的不断增大，对称式基坑的单宽涌水量q逐渐减小，整体趋势呈先快后慢。对称式基坑的单宽涌水量q与基坑土体的渗透系数k成正比，不受H、T1S、hT1、HT1 的影响。

参考文献：

[1] 童磊，谢康和，卢萌盟，等. 半无限含水层中带衬砌隧洞渗流解析研究[J]. 岩土力学， 2011， 32（1）： 304308.

TONG L， XIE K H， LU M M， et al. Analytical study of seepage flow into a lined tunnel in a semiinfinite aquifer [J]. Rock and Soil Mechanics， 2011， 32（1）： 304308. （in Chinese）

[2] 毛海涛，侍克斌，李玉建.无限深透水地基上土石坝坝基垂直防渗的保角变换渗流计算[J].水利水运工程学报， 2008（4）： 7177.

Mao H T， SHI K B， LI Y J. Seepage calculation of earthrockfill dam swith vertical cutoffwall on infinite deep pervious foundation by using transformation method [J]. Hydroscience and Engineering， 2008（4）： 7177. （in Chinese）

[3] CHOUDHARY M， CHAHAR B R. Recharge/seepage from an array of rectangular channels[J]. Journal of Hydrology， 2007， 343（1）： 7179.

[4] KOLYMBAS D， WAGNER P. Groundwater ingress to tunnelsthe exact analytical solution [J]. Tunnelling and Underground Space Technology， 2007， 22（1）： 2327.

[5] 曹净， 张丙军， 刘海明. 基坑悬挂式止水帷幕渗流的共形映射[J]. 工程勘察，2014（11）： 3438.

CAO J， ZHANG B J， LIU H M. Conformal mapping of unclosed cutoff curtain seepage in the foundation pit[J]. Geotechnical Investigation & Surveying， 2014（11）： 3438. （in Chinese）

[6] 陈永刚，张少琴.保角映射方法在复合材料断裂分析中的应用[J].太原科技大学学报， 2001， 22（2）： 97101.

CHEN Y G ， ZHANG S Q. Fracture analysis of orthotropic composite plate by conformal mapping method [J]. Journal of Taiyuan University of Science and Technology， 2001， 22（2）： 97101. （in Chinese）

[7] 程海霞， 李俊林.含曲線裂纹的各向异性板断裂问题[J].中北大学学报（自然科学版），2012（5）：503508， 529.

CHENG H X， LI J L. Fracture problem in anisotropic composite plate including curve crack[J]. Journal of North University of China（Natural Science Edition）， 2012（5）：503508，529. （in Chinese）

[8] 吴华.L（o）wner理论对动态断裂问题的应用初探[J]. 重庆电子工程职业学院学报，2010，19（5）：140143， 165.

WU H. Preliminary exploration on the application of L（o）wner theory in developmental fracture [J]. Journal of Chongqing Vocational & Technical Institute. 2010， 19（5）： 140143，165. （in Chinese）

[9] 王志良，申林方，姚激，高成杰.浅埋隧道围岩应力场的计算复变函数求解法[J].岩土力学，2010，31（Sup1）： 8690.

WANG Z L， SHEN L F， YAO J， et al. Calculation of stress field in surrounding rocks of shallow tunnel using computational function of complex variable method [J]. Rock and Soil Mechanics， 2010， 31（Sup1）： 8690. （in Chinese）

[10] 王立忠，吕学金.复变函数分析盾构隧道施工引起的地基变形[J].岩土工程学报，2007， 29（3）：319327.

Wang L Z， LV X J. A complex variable solution for different kinds of oval deformation around circular tunnel in an elastic half plane [J]. Chinese Journal of Geotechnical Engineering， 2007， 29（3）： 319327. （in Chinese）

[11] 蔚立元，陈晓鹏，韩立军，等.基于复变函数方法的水下隧道围岩弹性分析[J].岩土力学，2012（Sup2）： 345351.

YU L Y， CHEN X P， HAN L J， et al. Elastic analysis of surrounding rock for underwater tunnels based on functions of complex variables method [J]. Rock and Soil Mechanics， 2012（Sup2）： 345351. （in Chinese）

[12] 任保文.对称平板传输线分布电容的计算[J].物理通报， 2013（1）： 2426.

REN B W. Calculation on distributed capacitance of symmetrical slab transmission line[J]. Bulletin of Physics. 2013（1）： 2426. （in Chinese）

[13] COSTAMAGN E， FANNI A. Needle electrode fields with spacecharge effects[J]. Microwave and Optical Technology Letters， 2000， 26（5）： 321325.

[14] HSU J M， WU M L， LEE C T. Hybrid approach for quasistatic analysis of shielded strip lines[J]. Microwave and Optical Technology Letters， 1997， 14（2）： 111115.

[15] FRIEDLANDER S， SERRE D. Handbook of elliptic integrals for engineers and scientists [M]. Berlin： Springer， 2004.

[16] ELGANAINY M A. Flow underneath a pair of structures with intermediate filters on a drained stratum[J]. Applied Mathematical Modelling， 1986， 10（6）： 394400.