满足静态电压稳定增强要求的发电机最佳调整方法

徐兴东，王 蕾，邓晓帆，王 聪，孙建超

满足静态电压稳定增强要求的发电机最佳调整方法

徐兴东，王 蕾，邓晓帆，王 聪，孙建超

(山东理工大学电气与电子工程学院，山东 淄博 255000)

为增强电力系统的静态电压稳定性，同时最大限度地减小运行人员的操作工作量，提出了一种综合经济性和静态电压稳定性的发电机最佳调整模型。该模型以发电机参与调整台数最少和发电成本最小为目标，约束条件包括系统负荷裕度满足设定提升要求和电力系统安全运行要求。该问题的数学本质是一个多目标非线性混合整数规划问题。为实现上述问题的求解，首先以线性灵敏度方法快速估算所需调整出力的发电机，求解控制数量最少的整数规划问题。然后以发电成本最小为目标，利用线性规划法求解各台发电机的调整出力值。最后在IEEE39节点算例和IEEE118节点算例进行仿真验证，结果表明所提模型与求解方法能很好地解决系统的静态电压稳定性增强控制问题。

优化调度；负荷裕度；灵敏度方法；发电成本；线性规划

0 引言

近年来我国电力系统在电源结构[1-2]和电网结构[3]方面发生了重大变化，电力系统运行的不安全因素增加，系统经常运行在稳定边界附近。世界范围内也发生了多起因电压稳定问题导致的大面积停电事件[4-5]，造成了巨大的经济损失和严重的社会影响。因此，采取有效的增强控制措施提高电力系统的静态电压稳定性具有重要的意义。

学者们针对多种提高电压稳定性控制措施进行了研究，其中发电机有功出力优化具有较好的可控性，并且无需增添额外的设备，具有一定的实用性和经济性。关于对发电机有功出力调整提高电力系统负荷裕度的研究，现有处理方式分为两种[6]：第一种是将系统对负荷裕度的要求作为目标函数处理；例如文献[7-8]提出以最大化系统负荷裕度为目标，基于改进的粒子群算法[7]、交替优化算法[8]优化发电机有功出力，解决了以负荷裕度最大为目标的有功出力调度问题。这种处理方式所得的优化结果通常会以牺牲其他目标为代价，计算得到的结果不能满足实际系统运行的需要。第二种是将负荷裕度作为约束条件处理[9]；例如文献[10-12]以发电成本最小为目标，将负荷裕度作为约束条件建立优化模型，分别通过蚁群算法[10]、鲸鱼优化算法[11]和粒子群算法[12]对发电机有功出力进行优化。

在对发电机有功出力进行优化计算时亦可建立多目标或者多约束优化模型[13]。文献[14]建立了考虑电力系统发电成本和负荷裕度的多目标优化模型，在保证系统发电运行成本最优的同时得到理想的负荷裕度。文中在处理多目标问题时引入权重系数，但权重系数取值不理想时不易得到最优解。文献[15]提出一种以碳排放量和静态电压稳定性为约束条件，以网损最小为目标函数的发电权交易优化模型，将网损和有功出力转换成煤耗，直观体现节能减排的目的。上述文献综合考虑了电力系统的静态电压稳定性、环境和经济等因素，都取得了较好的优化效果，但所得结果包含参与调整的发电机数量较多，在线应用困难，因此在考虑经济性的同时，还应减少运行人员的工作量。关于减少控制数量的问题，文献[16]提出一种基于灵敏度快速筛选的电压稳定性预防控制选择方法，通过对灵敏度数值进行排序，快速筛选出优化效果较好的变量。文献[17]采用预选参与控制集的策略，使得优化问题的规模大为下降，间接实现了系统运行人员要求的最小控制数量的目标。

针对上述研究，本文提出采用最少数量的发电机、最低的发电成本进行有功出力调整，以提高电力系统的静态电压稳定性，本文主要贡献包括：

1) 建立了以发电机调整数量最少、发电成本最低为目标的发电机最佳调度多目标优化数学模型，通过采取最少的控制量实现电力系统经济性和静态电压稳定性的综合取优；

2) 提出了基于灵敏度方法和线性规划的分解求解方法，将最少的发电机调整台数和最低发电成本的多目标非线性混合整数规划问题转化成两个子问题求解，降低了原问题的求解难度；

3) 提出了不同调整台数的负荷裕度提升区间算法，通过负荷裕度提升需求可直接选择需要调整的发电机。

通过仿真算例结果与已有方法进行对比，验证了所提模型和算法能够实现在满足电力系统静态电压稳定性的同时，使得参与调整的发电机台数最少和发电成本最低。

1 发电机最佳调整模型

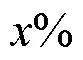
1.1 目标函数

1) 参与出力调整的发电机台数最少

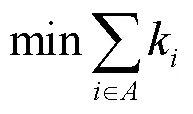
2) 发电成本最低

1.2 约束条件

1) 负荷裕度约束

目标函数(式(1)和式(2))需在负荷裕度满足指定条件下进行，即

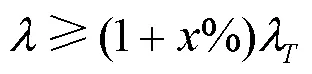
2) 连续潮流平衡约束

3) 发电机出力调整约束

调整过程中，忽略网络功率损耗，则参与调节的发电机有功功率调整量总和为零[19]，即

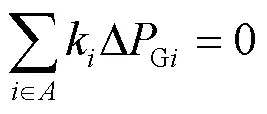
同时，调整过程应满足有功出力上下限约束，即

4) 静态安全运行约束

各节点电压幅值应满足约束：

电网企业数据中心通常和办公大楼共用部分基础设施，难以将非数据中心区域消耗的能源单独分离出来统计，本文提出了一种易于操作的计算方法，较为准确地估算出共用设施中与数据中心关联的部分能效，可简单有效地计算出数据中心的整体能效水平。同时，本文的统计方法易于在数据中心综合管理系统中实现，并给出了可行的测量标准与计算方法。

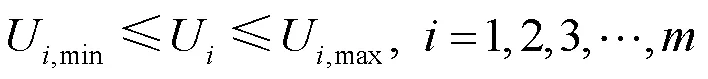
输电线路上视在功率的取值范围为

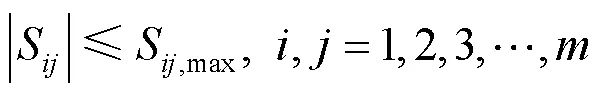
1.3 模型转化

本文所提模型中发电机是否参与出力调整可表示为0-1整数变量，发电机有功功率调整量有界且连续，因此该问题是一个多目标非线性混合整数规划问题。为降低该问题的计算复杂性，本文将多目标规划问题转化成两个子问题进行求解，算法步骤如图1所示。

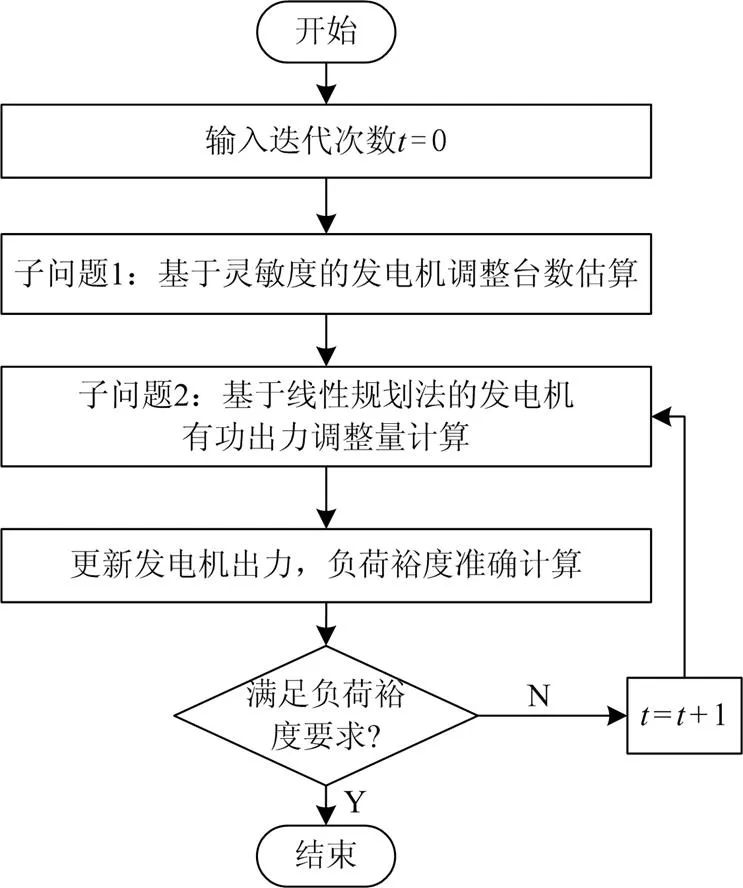
图1 满足负荷裕度要求的发电机调整流程图

margin requirements

子问题1：采用灵敏度方法快速估算不同发电机调整台数的负荷裕度提升区间，求解所提问题的整数变量；

子问题2：应用灵敏度法将原问题的非线性等式约束进行线性化处理，转化成线性规划问题来计算最优解。

2 灵敏度计算

电力系统的负荷裕度可定义为当负荷按照某种增长方式逼近电压崩溃点时，系统当前运行点到电压崩溃点的距离[20]。通过连续潮流法[21]可得到电压随负荷的变化趋势P-V曲线(如图2所示)，从而计算出负荷裕度。

图2 P-V曲线示意图

式(4)、式(5)可以简化成参数化潮流方程，如式(10)所示[22]。

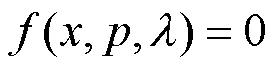
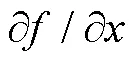
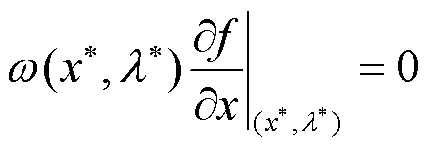
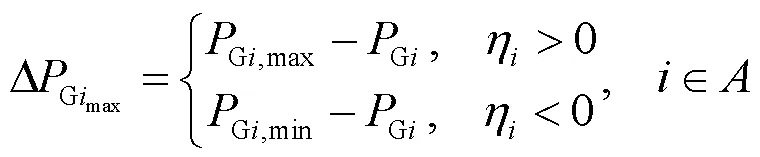
尽管部分发电机灵敏度数值较大，但其可调有功区间较小，因此本文采用式(14)来估算负荷裕度的最大变化量，并以此为依据将发电机进行排序。

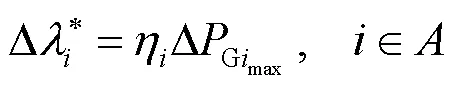
3 发电机最佳调整问题的求解

3.1 子问题1(发电机调整台数计算)

该子问题采用基于灵敏度的方法估算发电机调整台数，前文已经介绍了灵敏度方法及裕度估算，因此，为实现参与调整发电机台数的计算，本文构造了一个基于灵敏度的发电机调整台数估算子问题的数学模型，根据负荷裕度提升需求确定需要调整的发电机集合。

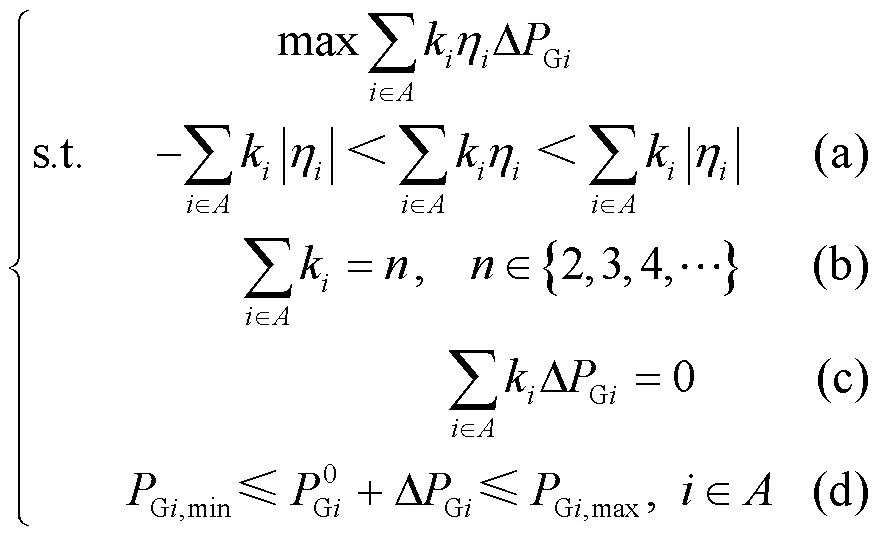
式中：为参与调整的发电机台数；式(a)保证了在选取发电机增强负荷裕度时其灵敏度数值要有正有负；式(c)保证了参与调整的发电机台数最少为2。

根据上述子问题的解可以得到不同台数发电机调整与负荷裕度提升范围的对应关系，以此作为依据，运行人员可根据提升需求选择对应的发电机，求解出所提问题的整数变量，将对应的发电机节点集合传送至下一阶段进行具体调节量的计算。

3.2 子问题2(发电机调节量计算)

该子问题以子问题1的解作为给定值，求解发电机有功出力的具体调节量。本文采用灵敏度方法，将负荷裕度约束线性化处理[23-24]，针对所提问题构造如下数学模型：

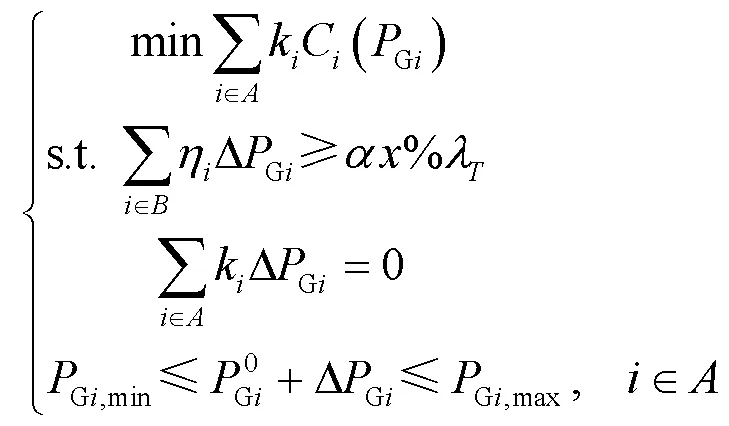
在本文中由于负荷裕度的计算是非线性的，因此需要检查电力系统在新的出力下是否满足系统负荷裕度的要求，若满足(式(3))，则计算结束，输出结果；否则，根据式(17)更新发电机有功出力，继续进行迭代计算。

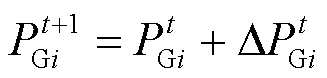
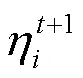
3.3 总体流程

本文所提发电机最佳调整模型具体流程如图3所示。

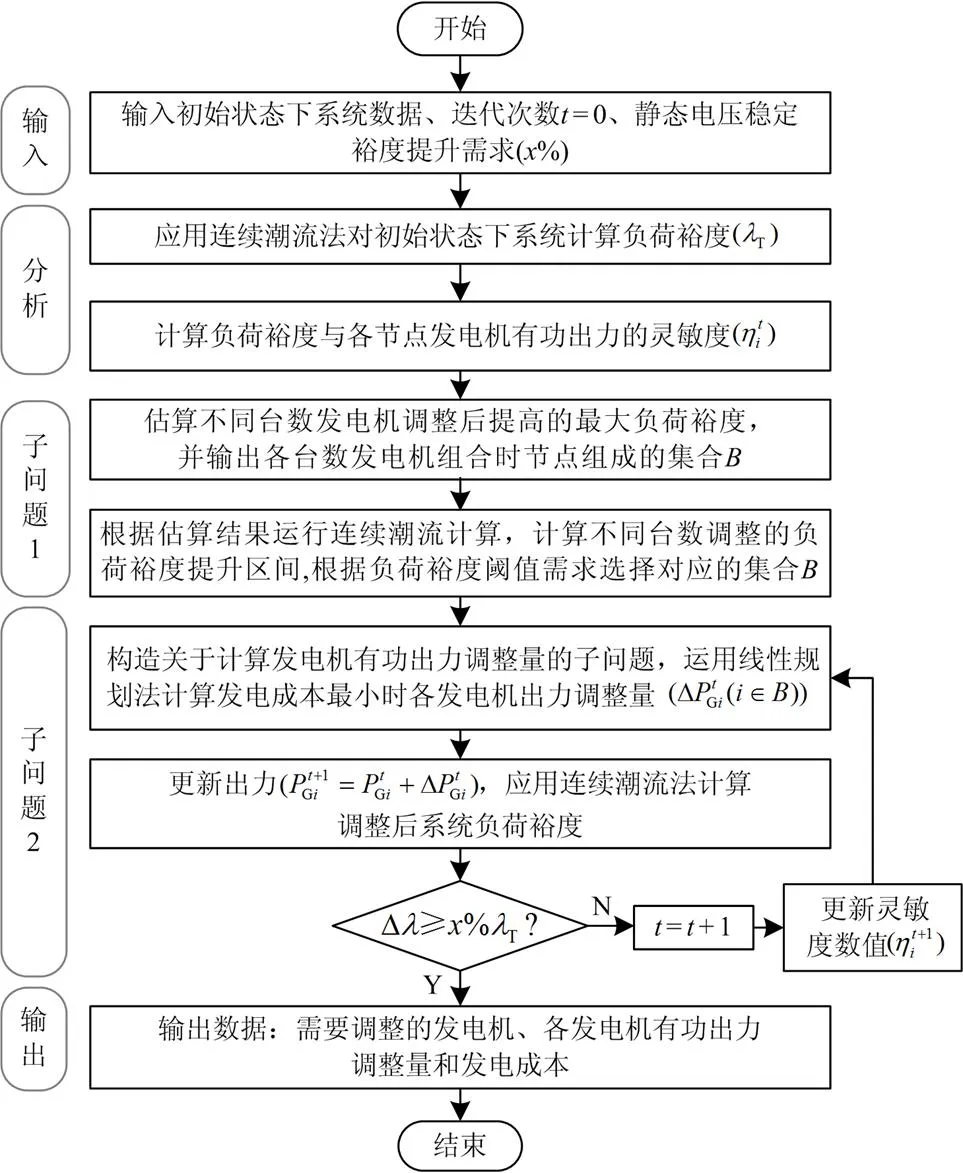
图3 发电机最佳调整流程图

4 算例分析

本文采用IEEE39节点算例和IEEE118节点算例验证本文方法的效果，仿真过程中发电机出力成本采用二次成本函数，成本系数见文献[25]。

4.1 IEEE39节点算例

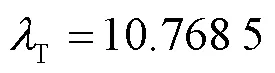
表1 负荷裕度提升比例与发电机调整台数的关系

在确定发电机台数的基础上考虑其成本问题，初始系统运行时发电成本为45 079.12美元。根据负荷裕度要求只需要采用两台发电机调整出力，对该问题应用子问题2所提模型计算，结果如表2所示。最终负荷裕度较初始系统提升了6.08%，初始状态电力系统和发电机调整后电力系统的P-V曲线对比如图4所示。

文献[10]同样采用灵敏度方法进行发电机有功出力调整，将负荷裕度提高一定的百分比作为约束条件，以最低发电成本作为目标函数，计算各发电机有功出力的调整量。按照文献[10]提出的方法对本算例进行优化，其结果与本文所提方法对比如表3所示。在满足负荷裕度提升比例的前提下，本文所采取参与调整的发电机数目最少，证明所提最少发电机数量参与调整的有效性。文献[10]计算中将全部发电机进行参与，在计算发电成本最小时做到了全局最优，而本文方法在确定最少发电机台数参与调整的前提下使发电成本最低，虽然较文献[10]方法来说发电成本较高，但所得结果较初始系统来说使发电成本降低了1.66%。因此，本文所提方法在满足负荷裕度要求的同时，保证了最少台数的选择和最低发电成本的综合取优。

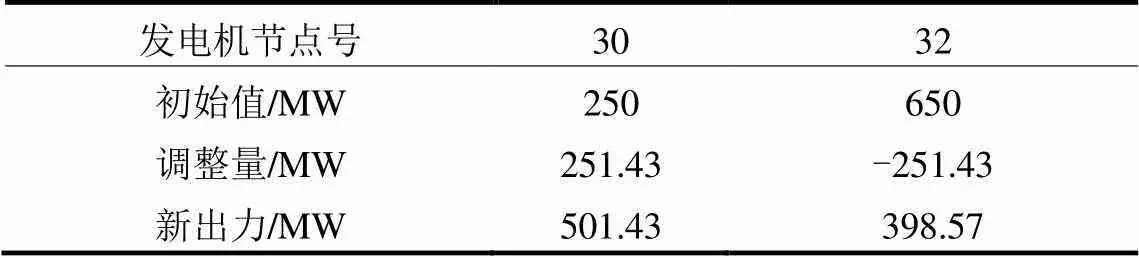
表2 发电机有功出力调整

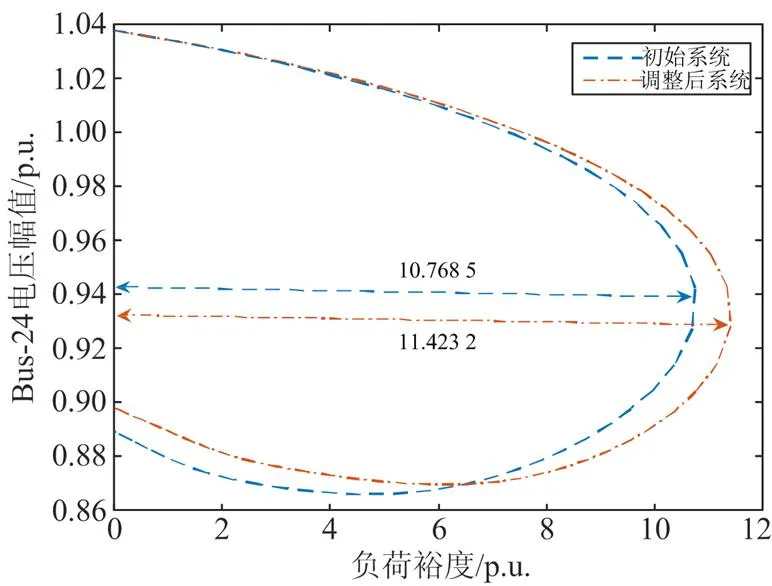
图4 初始电力系统和调整后电力系统的P-V曲线

表3 不同方法下的优化结果对比

4.2 IEEE118节点算例

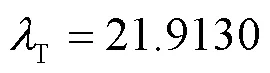
对各发电机中负荷裕度变化量进行计算，通过排序筛选出前6台发电机如表4所示。

表4 负荷裕度变化量排序

首先求解子问题1的模型，采取不同数量发电机进行调整时，可计算各发电机组合可提升的最大负荷裕度，计算结果如表5所示。

表5 不同发电机台数调整提升的最大负荷裕度

通过表5可以看出，当参与调整的发电机台数分别为2、3、4和5时，系统负荷裕度最小可提升5.9%、11.8%、14.2%和16.6%。

负荷裕度变化范围与最少发电机调整台数的对应关系如表6所示，调度人员可根据对负荷裕度的需求选择对应的发电机节点集合。

表6 负荷裕度提升比例与发电机调整台数的关系

若将负荷裕度提高12%，根据表6可采用4台发电机进行有功出力调整，即= {56,54,55,66}。根据子问题2所提方法对该问题进行计算结果，如表7、图5和图6所示。

表7 四台发电机有功调节量计算结果

图5为迭代过程中各发电机有功出力与对应的负荷裕度的变化，随着迭代计算的进行，负荷裕度逐渐增大，最终满足系统对负荷裕度的要求。图6为每次迭代计算时各发电机有功出力的调整量变化，迭代中调整量逐渐接近于零。

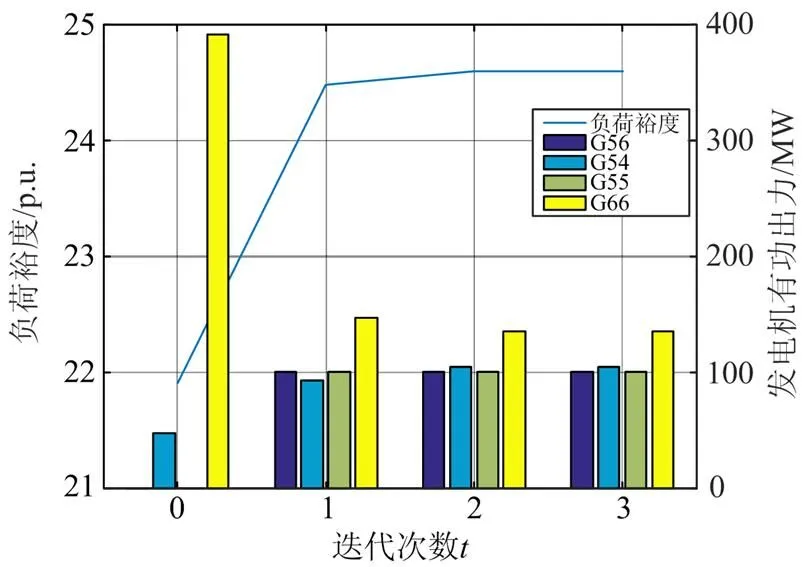
图5 迭代中各发电机有功出力变化

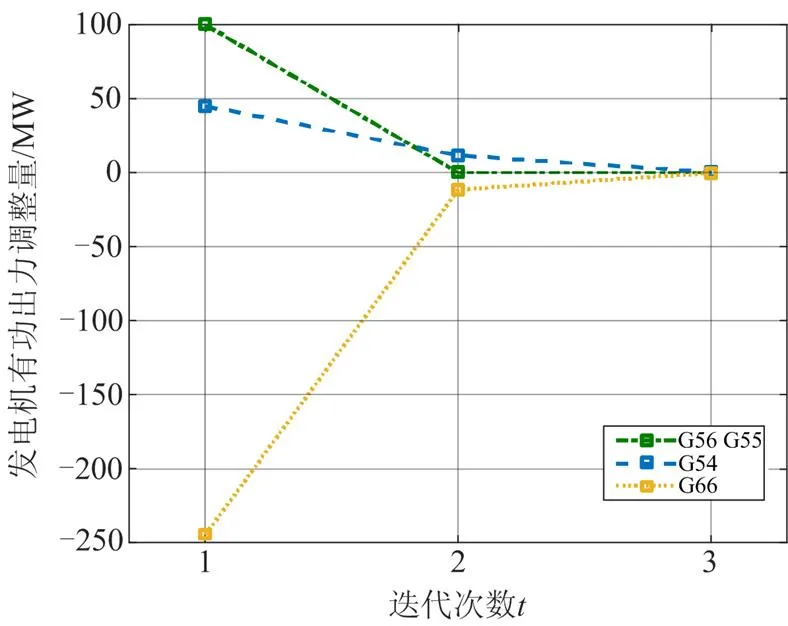
图6 迭代中发电机有功出力调整量变化

从图5和图6中可以看出，所提算法在很少的迭代次数内即可收敛，由于负荷裕度计算的非线性特点，在第1次迭代后得到的结果并不能满足系统对负荷裕度的要求，但第1次迭代后可大幅度地接近目标值。随着迭代次数增加，各发电机出力变化在小范围内波动可近似线性化，因此本文所提出的基于线性规划技术可有效地在控制范围内找到目标解。

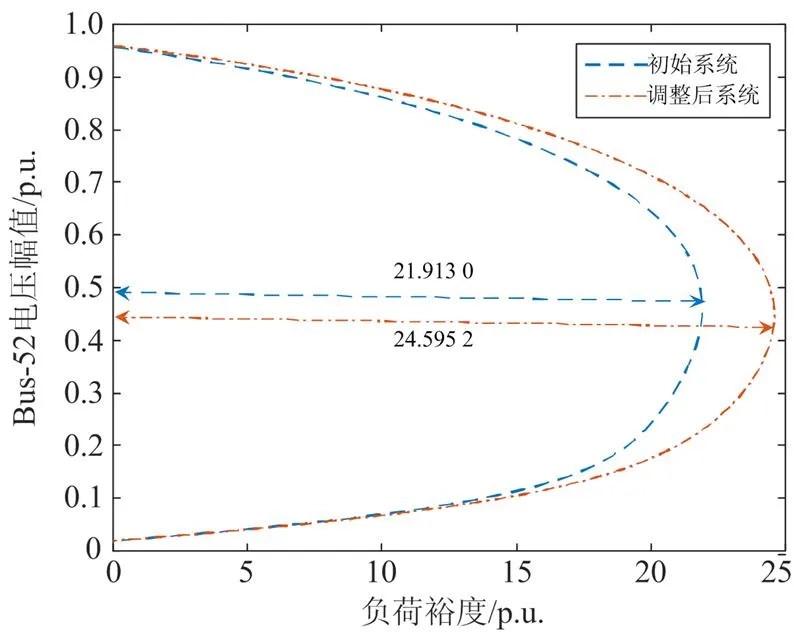
图7 初始电力系统和调整后电力系统的P-V曲线

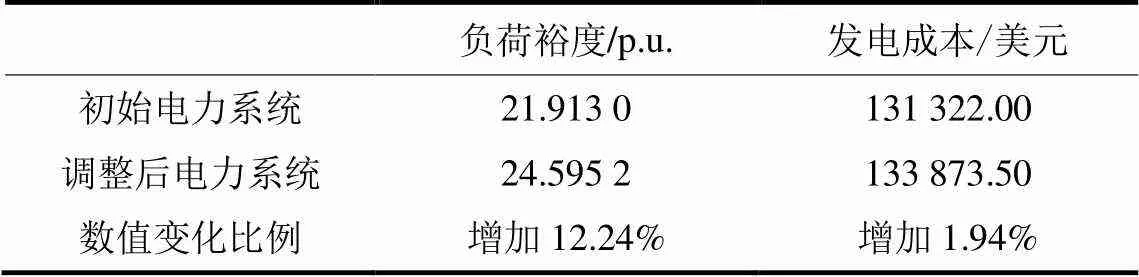
表8 调整前后负荷裕度和发电成本对比

与初始电力系统相比，优化后的电力系统负荷裕度提升了12.24%，发电成本增加了1.94%，满足系统对负荷裕度的要求。

为说明所得结果在满足负荷裕度要求的前提下发电成本最低，本文分别根据式(12)、式(18)计算了在调整后系统负荷裕度和发电成本对各台发电机有功出力的灵敏度，计算结果如表9所示，发电成本变化量如式(19)所示。

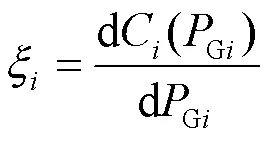
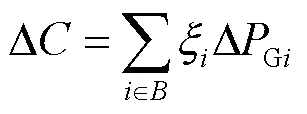
表9 基于灵敏度方法的最小成本验证

因此本文所提方法计算结果在满足负荷裕度要求的前提下，使得参与调整的发电机台数少，且优化调度结果具有较好的经济性。

5 结论

为提升电力系统静态电压稳定裕度，提出了一种基于最少台数发电机参与调整和最小发电成本的优化方法。运用负荷裕度对发电机有功出力的灵敏度法对各发电机进行筛选，确定最小发电机台数及其节点集合，运用线性规划法计算各发电机有功出力调整量。仿真结果表明，本文所提模型与求解方法能很好地解决系统满足静态电压稳定性增强要求的问题，所得结果使参与调整的发电机台数少，减少了运行人员的工作量，且优化调度结果具有较好的经济性。

本文对于静态电压稳定性的提高只考虑了发电机有功出力调整，而通过调整小数量的发电机来增加负荷裕度的程度是有限的，对于整个电力系统来说要综合应用各种预防控制措施，比如将变压器分接头调整、电网拓扑优化和电容器投切相结合来提高电力系统的负荷裕度，这也是今后值得研究的方向。

[1] 那广宇, 魏俊红, 王亮, 等. 基于Gram-Charlier级数的含风电电力系统静态电压稳定概率评估[J]. 电力系统保护与控制, 2021, 49(3): 115-122.

NA Guangyu, WEI Junhong, WANG Liang, et al. Probabilistic evaluation of power system static voltage stability with wind power uncertainty based on the Gram-Charlier expansion[J]. Power System Protection and Control, 2021, 49(3): 115-122.

[2] 郑宽, 徐志成, 鲁刚, 等. 高比例新能源电力系统演化进程中核电与新能源协调发展策略[J]. 中国电力, 2021, 54(7): 27-35.

ZHENG Kuan, XU Zhicheng, LU Gang, et al. Coordinated development strategy for nuclear power and new energy in the evolution process of power system with high penetration of new energy[J]. Electric Power, 2021, 54(7): 27-35.

[3] 赵红阳, 叶荣, 王秀丽, 等. 计及风电汇集系统静态电压稳定性的网储联合规划[J]. 智慧电力, 2021, 49(5): 15-20, 34.

ZHAO Hongyang, YE Rong, WANG Xiuli, et al. Coordinated planning of transmission network and energy storage systems considering static voltage stability of wind integration system[J]. Smart Power, 2021, 49(5): 15-20, 34.

[4] 刘伟. 电网严重故障下的电压稳定应对措施分析[J]. 电力系统保护与控制, 2020, 48(16): 163-170.

LIU Wei. Analysis of voltage stability countermeasures under a severe fault in a power grid[J]. Power System Protection and Control, 2020, 48(16): 163-170.

[5] ZENG Bo, OUYANG Shaojie, ZHANG Jianhua, et al. An analysis of previous blackouts in the world: lessons for China׳s power industry[J]. Renewable and Sustainable Energy Reviews, 2015, 42:1151-1163.

[6] 苏寅生, 鲍颜红, 阮晶晶, 等. 静态电压稳定预防控制的在线并行计算方法[J]. 电力系统及其自动化学报, 2017, 29(11): 87-91, 104.

SU Yinsheng, BAO Yanhong, RUAN Jingjing, et al. Online parallel calculation method for the prevention control of static voltage stability[J]. Proceedings of the CSU-EPSA, 2017, 29(11): 87-91, 104.

[7] 伍利, 陈少芳, 南海鹏. 基于IPSO优化发电调度的静态电压稳定分析[J]. 电力系统及其自动化学报, 2015, 27(4): 92-97.

WU Li, CHEN Shaofang, NAN Haipeng. Analysis of static voltage stability based on improved particle swarm

optimization to optimize generation dispatch[J]. Proceedings of the CSU-EPSA, 2015, 27(4): 92-97.

[8] 熊宁, 程浩忠, 马则良, 等. 基于负荷裕度最大化的发电出力优化(二)模型求解[J]. 电力系统自动化, 2009, 33(20): 43-46, 115.

XIONG Ning, CHENG Haozhong, MA Zeliang, et al. Generation dispatch optimization for maximizing loading margin part two model determination[J]. Automation of Electric Power Systems, 2009, 33(20): 43-46, 115.

[9] FENG Zhihong, AJJARAPU V, MARATUKULAM D J. A comprehensive approach for preventive and corrective control to mitigate voltage collapse[J]. IEEE Transactions on Power Systems, 2000, 15(2): 791-797.

[10] CHAKRABARTI S, JEYASURYA B. Generation rescheduling using ANN-based computation of parameter sensitivities of the voltage stability margin[J]. Engineering Applications of Artificial Intelligence, 2008(21): 1164-1169.

[11] AMROUNE M, BOUKTIR T, MUSIRIN I, et al. Power system voltage instability risk mitigation via emergency demand response-based whale optimization algorithm[J]. Protection and Control of Modern Power Systems, 2019, 4(4): 269-282.

[12] WU G Y, CHUNG C Y, WONG K P, et al. Voltage stability constrained optimal dispatch in deregulated power systems[J]. IET Generation, Transmission, and Distribution, 2007, 1(5): 761-768.

[13] YANG Yuerong, LIN Shunjiang, WANG Qiong, et al. Multi-objective optimal control approach for static voltage stability of power system considering interval uncertainty of the wind farm output[J]. IEEE Access, 2020, 8: 119221-119235.

[14] 陈政琦, 艾欣. 考虑电力系统发电成本和负荷裕度的多目标最优潮流方法研究[J]. 华北电力大学学报, 2019, 46(3): 26-32.

CHEN Zhengqi, AI Xin. Multi-objective optimal power flow algorithm for power generation cost and load margin[J]. Journal of North China Electric Power University, 2019, 46(3): 26-32.

[15] 杨胡萍, 严飞飞, 张力, 等. 考虑静态电压稳定约束的低网损发电权交易优化[J]. 电力系统保护与控制, 2017, 45(4): 45-49.

YANG Huping, YAN Feifei, ZHANG Li, et al. Optimization of low network loss generation right transaction considering steady state voltage stability constraint[J]. Power System Protection and Control, 2017, 45(4): 45-49.

[16] LI Shuaihu, TAN Yi, LI Canbing, et al. A fast sensitivity-based preventive control selection method for online voltage stability assessment[J]. IEEE Transactions on Power Systems, 2018, 33(4): 4189-4196.

[17] 赵晋泉, 江晓东, 张伯明. 一种在线电力系统静态稳定增强控制算法[J]. 中国电机工程学报, 2005, 25(8): 7-12.

ZHAO Jinquan, JIANG Xiaodong, ZHANG Boming. An on-line enhancement control algorithm for static stability in power system[J]. Proceedings of the CSEE, 2005, 25(8): 7-12.

[18] 鲍海波, 郭小璇. 考虑新能源发电不确定性的静态电压稳定故障筛选与排序方法[J]. 电力自动化设备, 2019, 39(7): 57-63.

BAO Haibo, GUO Xiaoxuan. Fault screening and ranking method of static voltage stability considering uncertainty of renewable energy power generation[J]. Electric Power Automation Equipment, 2019, 39(7): 57-63.

[19] 刘雨濛, 顾雪平, 王涛. 考虑静态安全距离的含风电电网安全优化调度[J]. 电力系统保护与控制, 2021, 49(15): 93-99.

LIU Yumeng, GU Xueping, WANG Tao. Optimal dispatching model for a wind farm integrated grid considering steady-state security distance[J]. Power System Protection and Control, 2021, 49(15): 93-99.

[20] 赵鹏辉. 考虑静态电压稳定的电力系统无功优化方法研究[D]. 济南: 山东大学, 2019.

ZHAO Penghui. Research on reactive power optimization method considering static voltage stability in power system[D]. Jinan: Shandong University, 2019.

[21] 王振浩, 由作宇, 黄亚磊, 等. 基于连续潮流法的含双端VSC-HVDC交直流系统负荷裕度分析[J]. 电力系统保护与控制, 2018, 46(6): 9-15.

WANG Zhenhao, YOU Zuoyu, HUANG Yalei, et al. Load margin analysis of hybrid AC/DC system with two terminal VSC-HVDC using continuous power flow method[J]. Power System Protection and Control, 2018, 46(6): 9-15.

[22] 王蕾. 大规模电力系统静态稳定增强的在线电网拓扑优化[D]. 天津: 天津大学, 2015.

WANG Lei. On-line network topology optimization for increasing static stability limit of large-scale power systems[D]. Tianjin: Tianjin University, 2015.

[23] 王涛, 胡丽, 刘子菡, 等.考虑灵活性需求与风电相关性的电力系统实时调度模型[J]. 全球能源互联网, 2021, 4(6): 585-594.

WANG Tao, HU Li, LIU Zihan, et al. Distributionally robust real-time dispatch model considering flexibility requirement and correlations of wind powers[J]. Journal of Global Energy Interconnection, 2021, 4(6): 585-594.

[24] YUN Zhihao, CUI Xinhui. Online preventive control method for static voltage stability of large power grids[J]. IEEE Transactions on Power Systems, 2020, 35(6): 4689-4698.

[25] ZIMMERMAN R D, MURILLO-SÁNCHEZ C E, THOMAS R J, et al. MATPOWER: steady-state operations, planning and analysis tools for power systems research and education[J]. IEEE Transactions on Power Systems, 2011, 26(1): 12-19.

Optimal generators re-dispatch method to meet the enhancement requirements of static voltage stability

XU Xingdong, WANG Lei, DENG Xiaofan, WANG Cong, SUN Jianchao

(School of Electrical and Electronic Engineering, Shandong University of Technology, Zibo 255000, China)

To enhance the static voltage stability of power systems and minimize the workload of the operators,an optimal generator re-dispatch model is proposed that takes into account economy and static voltage stability of power systems. The model aims to minimize the number of generators to be adjusted and the generation cost, and the constraints include the demand improvement load margin and a secure operating requirement for power systems.By nature, the problem is a multi-objective nonlinear mixed integer programming problem. To solve the problem, first, the generators to be adjusted are quickly estimated by a linear sensitivity method to solve the integer programming problem with the minimum number of controls.Then, the adjusted output value of each generator is determined by an available linear programming method with the objective of minimizing the generation cost.Finally, simulation analysis is carried out on the IEEE 39-bus and IEEE 118-bus power system. The results show that the proposed model and method can solve the enhancement control problem of static voltage stability.

optimal scheduling; load margin; sensitivity method; generation cost; linear programming

10.19783/j.cnki.pspc.211137

2021-08-19；

2021-09-24

徐兴东(1996—)，男，硕士研究生，研究方向为电力系统电压稳定与控制；E-mail: xxdong5445@163.com

王 蕾(1978—)，女，通信作者，博士，副教授，研究方向为非线性理论与计算、电力系统稳定性分析与控制。E-mail: wanglei@sdut.edu.cn

国家自然科学基金项目资助(51707109)；国家重点研发计划项目资助(2017YFB0902800)

This work is supported by the National Natural Science Foundation of China (No. 51707109).

(编辑 魏小丽)