考虑储热改造与最优弃能的风光火储低碳经济调度

臧紫坤，杨晓辉，李昭辉，袁志鑫，许 超，陈苏豪

考虑储热改造与最优弃能的风光火储低碳经济调度

臧紫坤，杨晓辉，李昭辉，袁志鑫，许 超，陈苏豪

(南昌大学信息工程学院，江西 南昌 330031)

大规模可再生能源消纳以及电力系统的低碳发展对减少火电机组调峰调频时的碳排放提出了更高要求。为提高系统风光消纳的经济性与火电机调峰的低碳性，提出一种考虑火电机组储热改造与风光最优弃能的风光火储分层优化调度方法。考虑风光反调峰特性，建立最优弃能约束模型，构建以电网净负荷方差最小为目标的上层模型，对净负荷曲线进行一次“削峰填谷”。为扩大火电机组调峰深度，考虑储热机组改造，建立碳交易成本模型。基于此，建立以系统总成本和碳交易成本最小为目标的下层模型，对净负荷曲线二次“削峰填谷”的同时，实现对系统经济与低碳的协同优化。基于算例分析，验证了所提出模型的合理性与有效性。

火电机组储热改造；最优弃能率；碳交易；削峰填谷；分层优化

0 引言

自2020年国家正式提出双碳目标以来，风电与光伏由于成本低、技术成熟且开发潜力巨大等因素发展迅猛，同时，由于风光的不确定性，系统的峰谷差大幅增加，严重限制着新能源的消纳能力[1-3]。为了提高新能源消纳水平，开展火电机组深度调峰灵活改造是重要手段，但火电机组调峰促进风光消纳会大幅增加机组碳排放[4]。因此，如何平衡风光消纳与机组调峰成本、碳排放之间的矛盾，对现代电力系统实现经济性与低碳性具有重要意义。

目前，有大量研究从提升电源侧灵活性的角度出发来提高风光消纳的效率。利用抽水蓄能、光热发电以及储热系统来平抑风光发电曲线，具有良好的电能时移特性，取得了较好的整体经济效益[5-7]。基于适当的弃风弃光可以提升系统经济效益的现实，有许多文献考虑了弃风弃光。文献[8-9]考虑弃风惩罚成本、火电机组运行成本等5个成本，构建了含多种抽蓄方式的系统调度模型。文献[10-11]基于弃能约束模型，提出一种考虑最优弃能率的风光火储双层优化调度方法。文献[12]建立了计及合理弃能的系统经济性最优模型。以上研究基于储能系统提升电源侧灵活性，考虑最优弃能时，仅以系统经济性最优为目标函数，并未考虑火电机组调峰时碳排放问题。

针对提升火电机组调峰深度问题，国内外学者做了大量工作。文献[13]通过抽汽储热改造技术提高锅炉低负荷稳燃效果，降低机组最小出力，从而进行深度调峰。文献[14-15]从优化控制系统、水冷壁安全防护的角度减少机组启停时间，利用改造煤粉供给系统、温度控制系统等措施提高机组爬坡速率，提高了系统应对可再生能源出力变化的能力。文献[16]通过经济成本分析指出，锅炉稳燃改造比快速启停和快速爬坡技术更具效益优势。文献[17-20]对火电机组储热系统的动力学模型进行了建模。目前已有文献分析了火电机组储热改造后参与系统发电的经济性[21]，鲜有文章深入探讨火电机组储热改造参与风光火储系统发电的低碳性及其原因。

鉴于此，本文提出一种考虑最优弃能率与火电机组储热改造的风光火储低碳经济调度方法。以电网净负荷方差最小为上层目标，以系统总成本和碳交易成本最小为下层目标构建分层优化模型，对负荷进行二次“削峰填谷”，改变弃能约束上限，结合算例，探索储热改造效益范围。

1 储热改造及合理弃能对机组调峰的影响分析

1.1 火电机组储热改造原理及运行模型

1.1.1改造原理

燃煤火电机组内部能量传递主要有三个过程：1) 通过锅炉燃烧煤产生的热量给水加热形成高温高压蒸汽，随后蒸汽流入蒸汽轮机高压缸做功；2) 高压缸做功完成后的蒸汽流入锅炉再形成热蒸汽，之后导入蒸汽轮机中的中压缸与低压缸做功；3) 冷凝塔将低压缸做功完成后的气体冷却为液态水，期间，液态水通过缸中抽取的部分蒸汽加热为高温给水。

传统火电机组的锅炉、蒸汽轮机、发电机等各个环节通过热能流动紧密耦合，锅炉稳燃条件及机械边界承载能力等因素极大制约火电机组出力调整范围，从而限制机组深度调峰能力。因此，本文基于热循环原理，在蒸汽动力循环中加入高低温双循环储热装置对热能进行存储与释放，在保证稳燃条件的情况下，对机组各环节之间的热能解耦，实现火电机组的出力灵活性改造，改造后的火电机组能量流图见附图1。

1.1.2运行模型

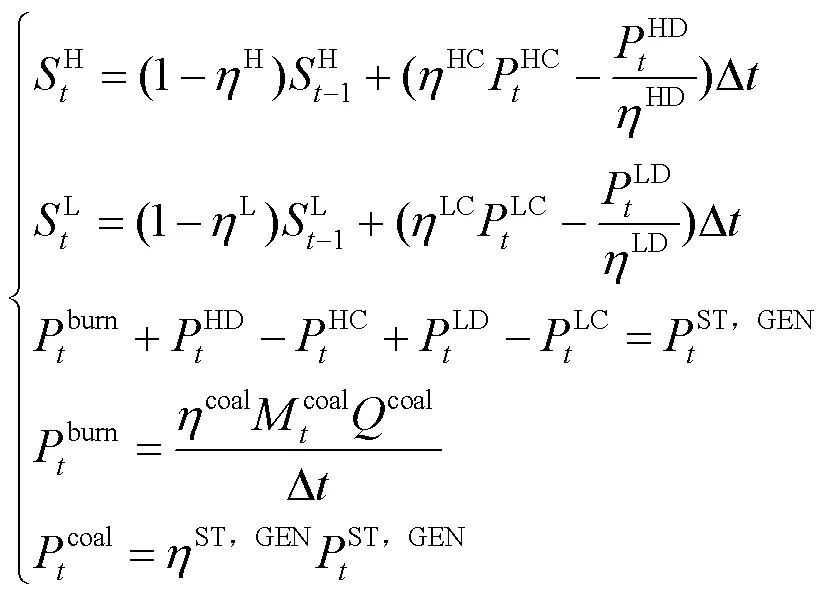
1.2 储热改造与合理弃能对机组调峰的影响分析

随着“碳达峰、碳中和”被提上日程，新能源发电规模在急剧扩大，其中，风光发电由于技术成熟、政策支持、市场环境优越等因素发展最快。但其发电的随机性、间歇性、反调峰性导致并网消纳时可能会增大受端电网的峰谷差，有时为了消纳更多的风光发电需要火电机组进行深度调峰，从而造成机组调峰成本大幅增加，同时，传统深度调峰方式会大幅提高机组的单位碳排放和发电能耗[4]。因此，本文从风光出力特性与火电机组深度调峰特性入手，分析合理弃能与储热改造对机组调峰的影响。本文引入净负荷定义，将并入受端电网的风光出力等效为外部电源，相当于负的电荷，受端电网的净负荷等于初始负荷与并网的风光出力之差[22-23]。

传统的火电机组调峰一般分为基本调峰、不抽油深度调峰、抽油深度调峰。传统火电机组在深度调峰时，由于锅炉稳燃接近最小工况，导致单位碳排放大幅增加。因此，本文结合火电机组储热改造技术，在保证机组稳燃的前提下，通过高、低温储热装置稳定机组出力。如图1，在1时段，高、低温储热装置储存热功率，等效于增加负荷，吸收机组多余出力，在2与3时段，储热装置释放热功率，等效于减小负荷，降低机组出力，有效提高单位煤量的发电量。

图1 净负荷峰谷分析图

本文一方面在确保风光并网效益的前提下，考虑合理弃能，平抑净负荷出力波动；另一方面考虑机组储能改造，稳定机组出力，减少火电机组深度调峰，从而使系统运行经济低碳。

2  考虑机组改造调峰与最优弃能的低碳经济调度模型

本文以减少碳排放量和运行调度成本为目标，利用储能系统与储热改造技术平衡风光消纳与火电机组调峰增加碳排放之间的矛盾，建立考虑火电机组储热改造与风光消纳协同促进碳减排的风光火储分层优化调度模型，模型流程如图2所示。

图2 分层优化调度流程图

上层模型在满足抽蓄储能系统运行约束、风光弃能约束等条件的基础上，以受端电网净负荷方差最小为目标，对各个时段的弃风弃光进行优化，得到各个时段的最优弃能率以及综合弃能率，同时将各储能系统充放电功率与净负荷曲线输入到下层模型。

下层模型以电网调度成本以及碳排放成本为目标函数，基于上层模型传递的净负荷曲线以及储能系统充放电功率，在满足火电机组系统运行约束、储热改造系统运行约束等条件时，对储热系统储放量、火电机组燃煤量以及出力进行优化，使碳排放成本、燃料成本、机组启停成本、旋转备用成本、环境保护税等成本最小。

2.1 碳交易机制

碳交易机制通过市场化交易碳排放权来限制温室气体的排放，是实现“双碳”目标的有效措施之一。目前，碳排放权交易主要分为项目型交易与配额型交易。项目型交易主要指开展绿色发展项目来实现碳减排；配额型碳交易是政府有关部门为碳排放源分配碳排放额度。当排放源实际碳排放高于分配额度时，碳交易为正，即碳排放源需要支付高额罚款来购买碳排放权；而当排放源实际碳排放低于分配额度时，碳交易为负，即碳排放源可出售碳排放权[24]。本文考虑配额型碳交易。

碳排放源在满足碳排放控制总量的前提下，自主购买或售出碳排放权，可有效鼓励各发电企业降低碳排放量。本文根据我国试运行的碳排放交易机制，采用基准法来计算初始配额。依据《全国碳排放交易额度分配方案(讨论稿)》中我国主要调峰机组的容量级别、压力参数以及燃料类别，划分11个基准[25]为不同机组分配碳排放额度，具体计算公式为

火电机组实际碳排放量计算公式为

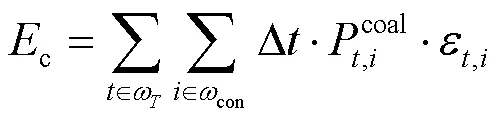
2.2 上层优化模型

2.2.1目标函数

上层目标主要是使受端电网的净负荷方差最小，即：

2.2.2约束条件

考虑上层模型的约束条件时，除了风光预测出力的约束之外，还需考虑以下约束。

1) 弃风弃光约束

2) 储能系统充放电约束

由于储能系统工况限制，不仅充放功率有最大最小约束，且充放不能同时进行，因此要满足式(7)。

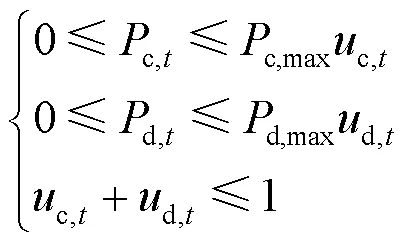
3) 储能系统荷电约束

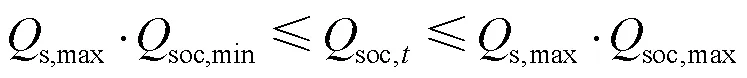
2.3 下层优化模型

2.3.1目标函数

为了兼顾调度系统的低碳性与经济性，下层目标函数主要考虑火电机组燃料成本、碳交易成本、机组启停成本、旋转备用成本、环境保护税、风光储系统运行成本以及风光消纳带来的环境收益。

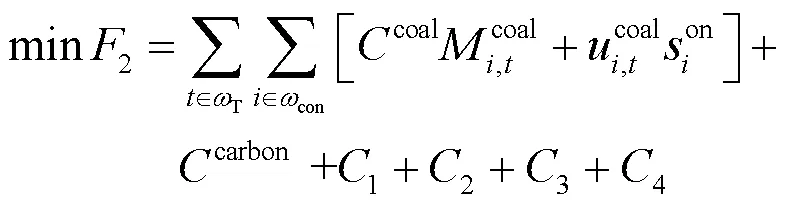
1) 旋转备用成本

由于风光出力随机性带来一定的预测误差，系统必须考虑一定容量的旋转备用。火电机组的旋转备用成本计算公式为

2) 环境保护税

3) 风光储系统运行成本

风光储系统的运行成本主要由风光发电站的维护成本以及储能系统装置的折旧成本构成，可由式(13)计算而得。

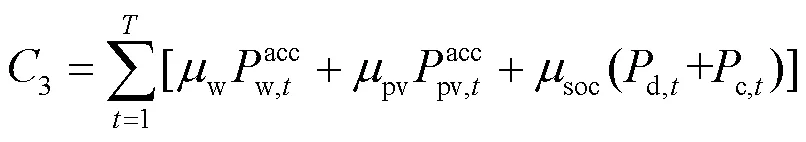
4) 风光消纳收益

考虑风光等清洁能源的并网消纳能有效降低硝硫等污染气体的排放量，并且储能系统的投运也会减小污染气体的排放，从而带来环境收益。其计算公式为

2.3.2约束条件

针对下层模型不仅需要火电机组运行时的常规约束，还需满足储热改造系统有关约束以及输电线路功率约束。

1) 电功率平衡约束

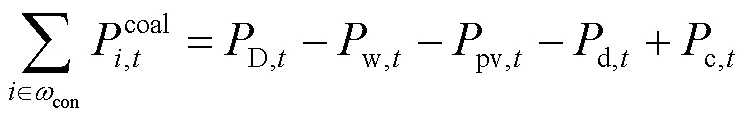
2) 火电机组运行约束

火电机组出力约束表示为

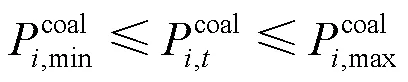
火电机组出力爬坡约束可表示为

火电机组最小启停时间约束为

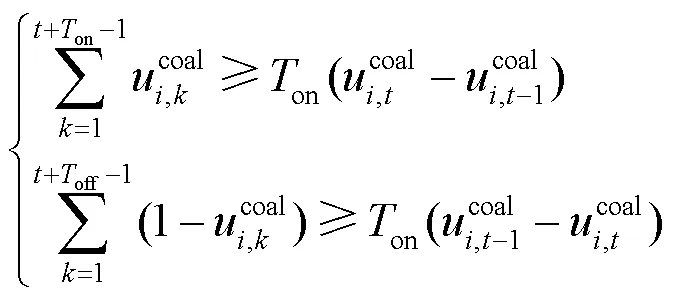
3) 系统旋转备用约束

4) 储热系统约束

高低温储热系统容量约束如式(20)所示。

5) 锅炉煤燃烧质量约束

高/低温储热系统储放约束以及状态约束可用式(22)表示。

在本文构建的下层模型中，除了满足以上模型之外，还需满足蒸汽轮机做功发电功率约束[21]、储热机组出力约束以及线路传输功率约束[8]。

2.4 模型求解算法

本文所建上下层模型均为混合整数线性规划模型，故可在Matlab环境下基于yalmip平台，调用gurobi求解器计算。具体求解流程见图3。

1) 输出入风光出力、负荷、弃能约束上限及改造机组系统相关基础数据；

2) 求解上层模型，输出储能系统各时段充放电功率、风光各时段最优弃能率及优化后净负荷曲线；

3) 结合上层模型输出的净负荷及储能系统充放电功率，输入考虑储热改造后机组调峰的下层调度模型；

4) 利用gurobi求解器计算下层模型得到系统运行总成本以及机组调峰时的碳排放量；

5) 改变风光弃能约束上限，重新计算上层优化负荷模型与下层经济低碳调度模型，如此反复，当风光弃能约束上限大于1时，输出结果。

3 算例分析

3.1 算例参数设置

本文采用改进的30机系统[10]进行算例分析，该系统包括4台火电储热改造机组、1个风电场、一个光伏电站和1个储能电站，总容量分别为1 400 MW、400 MW、200 MW、450 MW。负荷与风光出力预测如附图3所示。

图3 本文模型求解流程图

碳交易价格为140元/t,储热改造机组相关参数：热损失率为0.031%/h；储放热效率为98.5%；煤燃烧效率为89%；煤燃烧热值为29.3 MJ/kg；热转换效率为40%；煤价格500元/t。下层模型其他主要参数见表1与附表1，火电机组其余参数引用文献[10]。

3.2 最优风电消纳结果分析

通过对上层模型的优化求解，得到风电、光伏的最优弃能率分别为6.93%和7.07%，总最优弃能率为7%。同时，优化前后的净负荷曲线以及储能系统各时段储放电量见图4，各时段风光弃能与并网功率见图5。

从图4可知，当不考虑储能系统仅考虑最优弃能时，在一定程度上降低负荷的峰谷差。而在考虑储能系统之后，储能系统在00：00—04：00及15：00—18：00时段充电对系统起到填谷的作用，在09：00—13：00及19：00—22：00时段对系统起到削峰的作用。优化前后净负荷最大峰谷差从850 MW降至461 MW，有助于系统稳定运行，同时降低系统调峰成本。

表1 下层模型其他主要参数

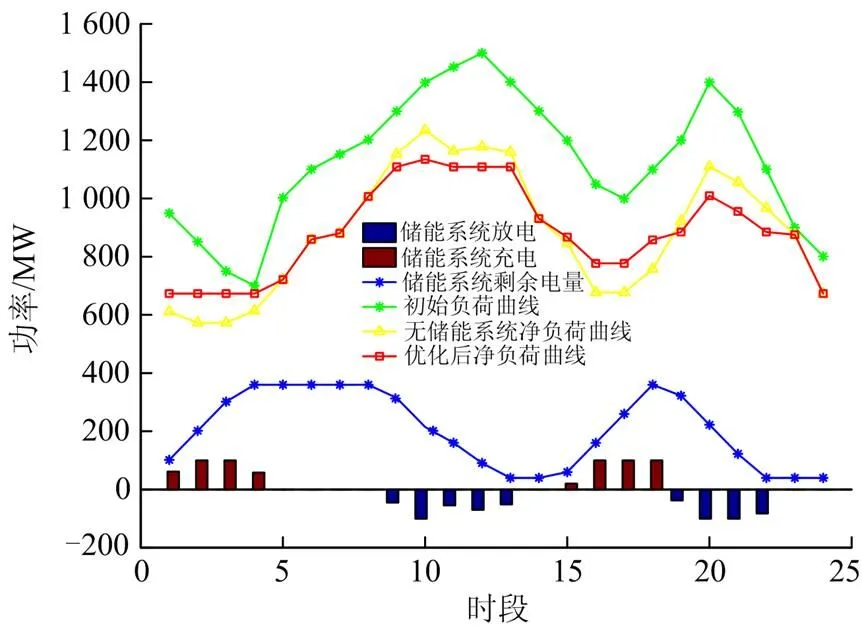
图4 储能系统运行及优化前后负荷对比

图5 各时段风光并网与弃能情况

从图5可知，弃风主要发生在00：00—04：00及23：00—24：00时段，这主要是因为风电的反调峰特性所致，晚间负荷急剧减少，若风电全额消纳导致负荷曲线波动更大，进一步说明考虑风光最优弃能的必要性。而弃光时段仅在16：00—18：00时段，这与日间光伏出力有助于平抑负荷出力曲线有关。

3.3 机组储热系统分析

为分析机组储热系统对一次调整后净负荷的平抑效果，得到高、低温系统在各时刻的储放热曲线，如图6所示，其中一次调整后净负荷为上层模型输入到下层模型的净负荷。

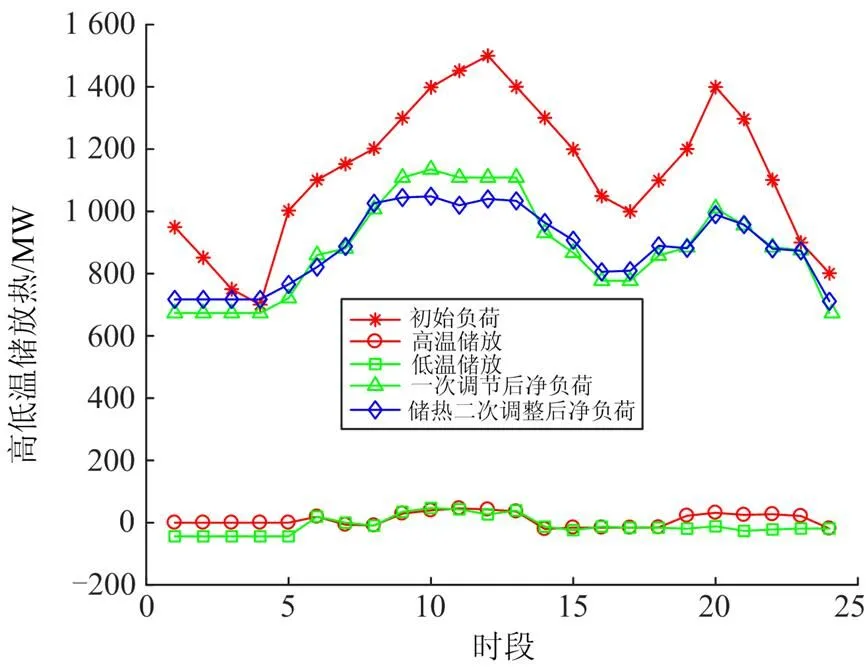
图6 储热系统储放热过程

由图6可知：在00：00—05：00及16：00—17：00时段负荷低谷时段，低温系统对锅炉产生的热量进行储存，减少汽轮机的进汽量，降低机组出力，从而系统对负荷曲线进行“填谷”；而在08：00—13：00时段，高低温系统则释放之前存储的热量，增加汽轮机的进汽量，提高机组出力，从而系统对负荷曲线进行“削峰”。经过储热系统二次“削峰填谷”，负荷曲线较一次调整后的净负荷曲线更为平缓。

3.4 不同模型低碳性对比分析

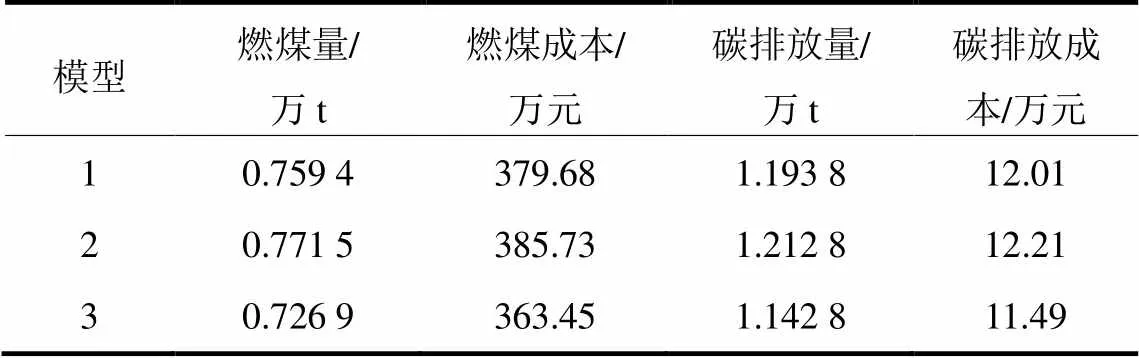
从图7及附表1可知，模型3比模型1、模型2碳排放降低510 t和700 t，煤燃量也有所下降。模型3与模型2比较说明储热机组改造能使锅炉产生的热量得到充分利用，减少耗煤，从而减少碳排放。模型1与模型2相比燃煤量与碳排放均有小幅下降，说明仅考虑最优风光弃能的减排效益略大于仅考虑储热机组改造带来的减排效益。

为了分析模型3中火电机组减少碳排放的机制，得到3种模型火电机组各时段的碳排放量，见图8所示。对比模型1与模型3可知，由于未考虑弃风导致净负荷峰谷差增大，使得火电机组调峰程度增加，而由于储热装置的容量限制，火电机组的出力波动并不能有效缓解。对比模型2与模型3，在00：00—08：00时段，模型2的碳排放较低，这是因为储热装置吸收锅炉热量时略微增加了火电机组的燃煤量，但在08：00—24：00时段，储热装置对火电机组锅炉系统热量有效增放调节，减少机组燃煤量，从而减少碳排放。

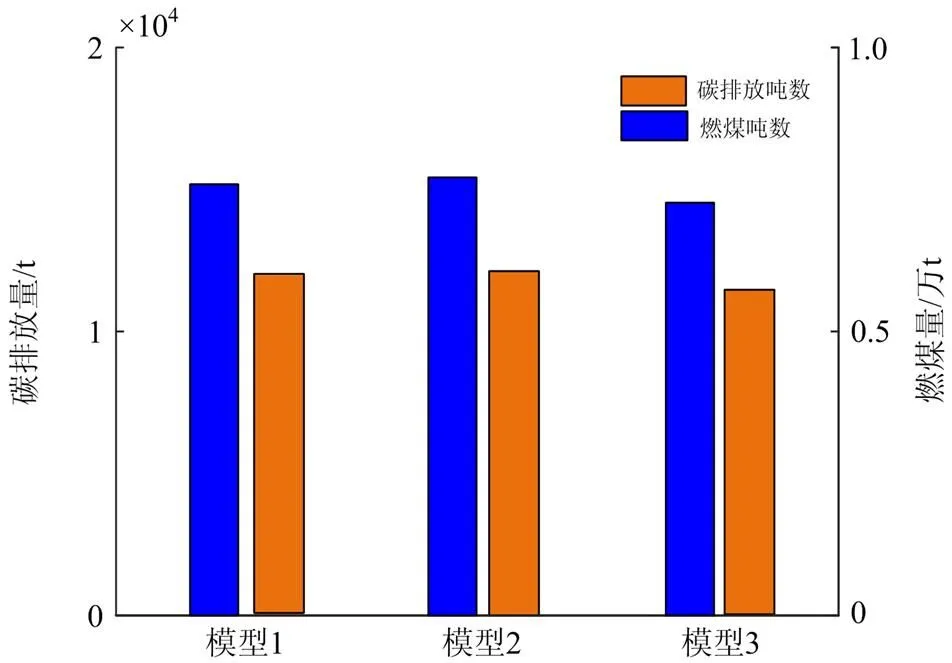
图7 3种模型燃煤及碳排放对比

图8 3种模型各时段碳排放对比

3.5 不同模型经济性对比分析

为了检验本文所提分层模型的经济、环保的合理性，下文选择3种模型对比分析：1) 低碳交易机制下，考虑风光全网消纳和机组储热改造的低碳经济调度模型；2) 低碳交易机制下，仅考虑风光最优弃能的低碳经济调度模型；3) 低碳交易机制下，考虑风光最优弃能和机组储热改造的低碳经济调度模型(本文模型)。3种模型运行的经济结果如表2所示。

从表2可知，模型3的总成本最小，比模型1与模型2分别降低了17.59万元、26.32万元，降幅分别为4.29%与6.29%，这主要是因为考虑最优弃能时既充分利用风光发电，又平抑了负荷波动，机组启停成本与模型1与模型2比较分别降低了2.5万元、4.2万元。此外，储热机组改造对负荷进行二次调节使负荷曲线更平缓，锅炉燃烧稳定性提高，单位发电耗煤量减少，降低火电机组煤耗，碳排放成本也略有降低。

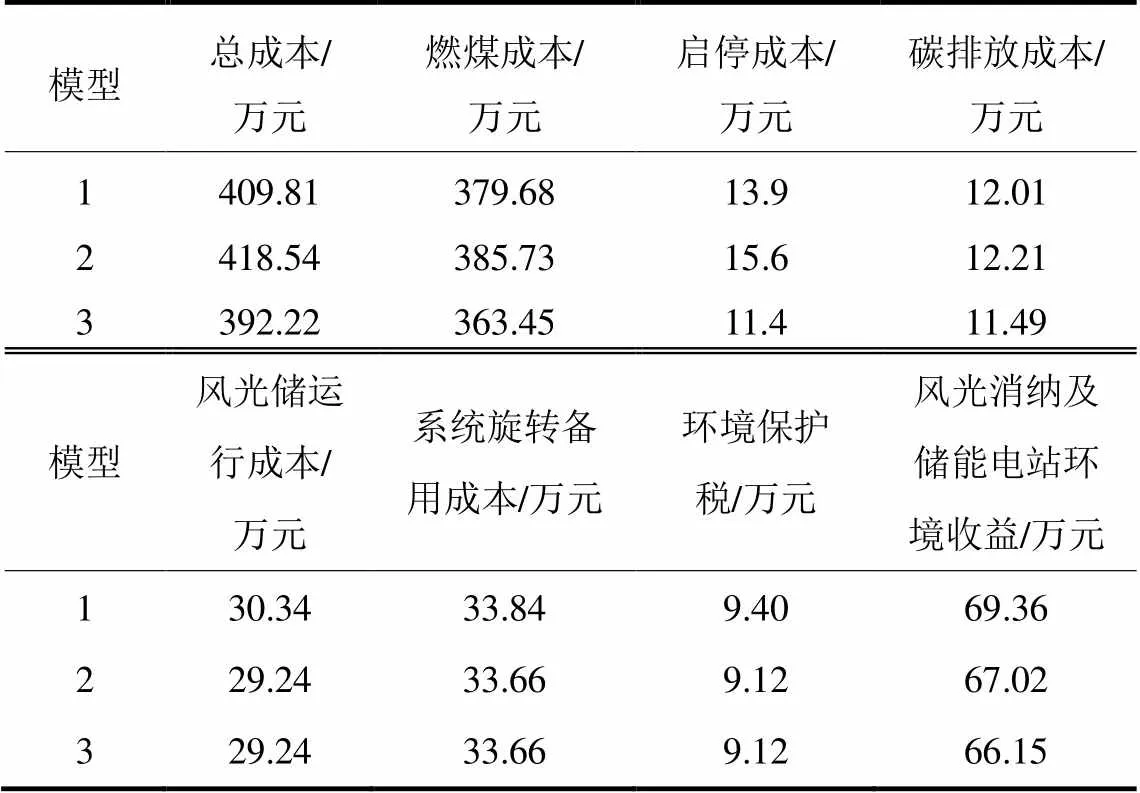
表2 3种模型的调度结果对比

3.6 弃能上限约束对系统运行的影响分析

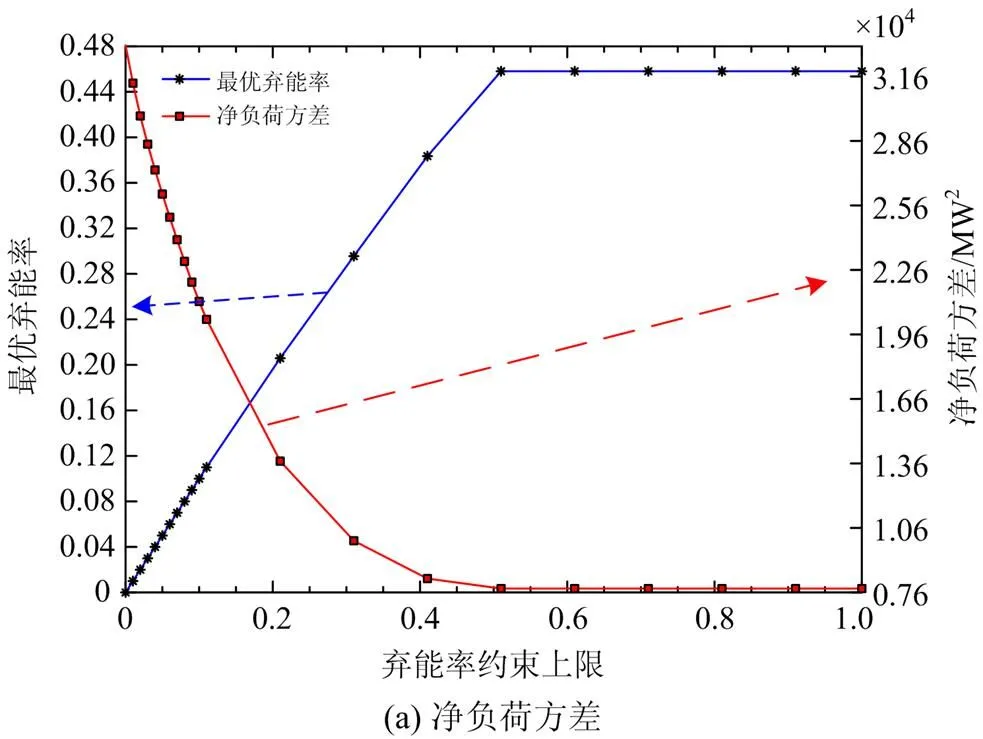
为分析弃能率约束对模型3中碳排放及系统总运行成本的影响，说明储热改造后的经济、环境效益，本文改变弃能率上限，得到模型3净负荷方差、模型2与模型3碳排放成本及系统总成本变化曲线，如图9所示。

1) 由图9(a)可知，随着弃能约束上限的增大，净负荷方差先逐步减小后趋于不变，净负荷曲线波动性先越来越小后趋于不变，而风光总弃能率却不断上升后趋于不变。这是由于模型3中的上层模型以净负荷方差最小为目标函数，在弃能率为0.5之前，以舍弃更多的风光发电为代价保证净负荷方差逐步减小，从而使净负荷曲线越平缓，而在弃能率为0.5之后，由于弃能约束已经达到调节净负荷方差的最大限度，故净负荷方差以及弃能率均趋于定值。

2) 对于弃能率约束对模型3中碳排放及总运行成本的影响，由图9(b)可知：在弃能率为0.07之前，随着弃能率上升，模型3系统总成本与碳排放成本均下降；弃能率为0.07～1，随着弃能率上升，模型3系统总成本与碳排放成本均先上升后趋于不变。结合图9分析其原因：弃能率为0～0.1，舍弃的风光发电量较少，净负荷方差显著下降，负荷曲线波动变缓速率偏大，锅炉燃烧稳定性越高，系统稳定运行程度越来越高，从而使得单位发电耗煤量减少，碳排放量减少，且系统稳定运行时的收益增量大于风光损耗增量；而弃能率为0.07～0.5，舍弃的风光发电量较多，虽然净负荷方差仍在下降，锅炉燃烧稳定性不断提高，单位发电耗煤量减少，但舍弃的风光发电使发电总量大幅提高，总碳排放量增加，系统总运行成本也不断提高；在弃能率为0.5之后，弃能率不变，净负荷方差不变，净负荷曲线不变，使得碳排放与总成本也不变。

3) 对于储热改造后的经济、环境效益分析。针对图9(b)，对比模型2与模型3的曲线变化可知，在同一弃能约束条件下，模型2的碳排放成本与系统总成本在弃能率为0.22之前均略高于模型3，在0.22之后与模型3重合。这主要是因为弃能率在0.22之前，净负荷方差较大，净负荷曲线波动较大，锅炉燃烧稳定性不高，机组储热改造对负荷进行二次“削峰填谷”，提高单位煤燃烧的发电量，减少碳排放及总成本。而弃能率在0.22之后，由于净负荷方差较小，净负荷曲线波动较平缓，储热改造装置对净负荷无二次“削峰填谷”的作用，故碳排放及总成本不减小。

4 结论

为消纳更多风光发电，同时减少火电机组调峰的碳排放和系统运行成本，本文提出了一种考虑火电机组储热改造与最优弃能的风光火储低碳经济调度方法，主要内容如下：

1) 以净负荷方差为上层模型目标函数，构建弃能约束模型，通过合理弃能以及储能充放电优化对负荷曲线进行一次“削峰填谷”优化。下层模型引入碳交易机制，以总成本为目标函数，对机组出力、碳排放进行优化，储热系统通过合理储放锅炉热量，实现火电机组调峰时的低碳性，间接对净负荷曲线进行二次“削峰填谷”平抑。

2) 根据仿真结果，本文模型相比仅考虑最优弃能、考虑储热改造全网消纳的总成本及碳排放成本分别降低26.32万元、4.2万元和17.59万元和2.5万元，兼顾了电能生产的经济性与低碳性。其次，得到本文实例的最优弃能率为0.07，同时对比模型2与模型3，得到本实例中机组储热改造可获益的弃能率为0～0.22。

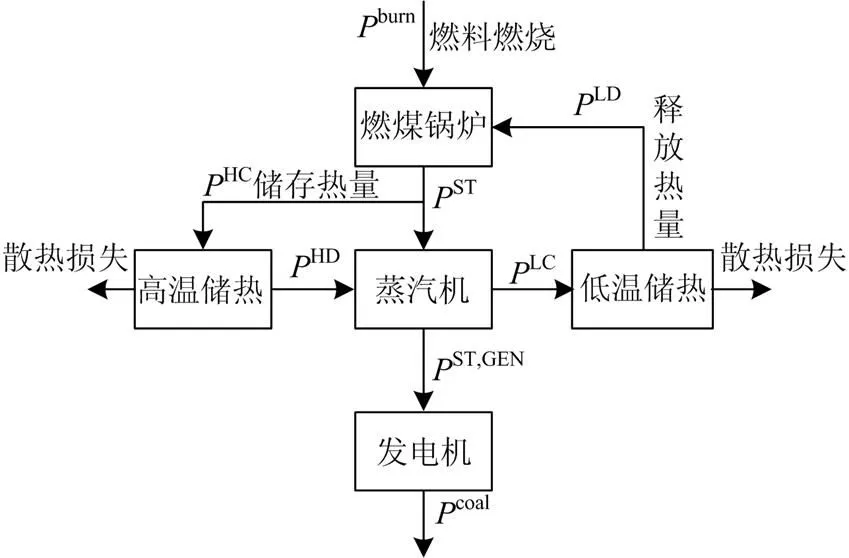
附图1 火电机组储热改造能流示意图

Attached Fig. 1 Technical parameters of heat storage transformation

附图2 多场景净负荷曲线图

Attached Fig. 2 Net load curves in multiple scenarios

附图3 负荷与风电出力预测曲线

Attached Fig. 3 Load and wind power output prediction curve

附表1 3种模型的碳排放结果对比

Attached Table 1 Comparison of carbon emission results of three models

模型燃煤量/万t燃煤成本/万元碳排放量/万t碳排放成本/万元 10.759 4379.681.193 812.01 20.771 5385.731.212 812.21 30.726 9363.451.142 811.49

附表2 机组储热改造技术参数

Attached Table 2 Technical parameters of heat storage transformation

机组序号机组最大出力/MW最大燃煤量/t最小燃煤量/t蒸汽轮机最大进汽量/MW蒸汽轮机最小进汽量/MW储热系统最大容量/MWh/(t/MWh)/(t/MWh) 1600190951 5002581 5000.8270.86 2～330094457501297500.8750.94 42006934500865001.0181.03

[1] 应益强, 王正风, 吴旭, 等. 计及新能源随机特性的电网深度调峰多目标策略[J]. 电力系统保护与控制, 2020, 48(6): 34-42.

YING Yiqiang, WANG Zhengfeng, WU Xu, et al. Multi-objective strategy for deep peak shaving of power grid considering uncertainty of new energy[J]. Power System Protection and Control, 2020, 48(6): 34-42.

[2] 邓杰, 姜飞, 涂春鸣. 美国NIST互操作性智能电网框架分析与启示[J]. 电力系统保护与控制2020, 48(3): 9-21.

DENG Jie, JIANG Fei, TU Chunming. Study of NIST’s interoperable smart grid technology architecture[J]. Power System Protection and Control, 2020, 48(3): 9-21.

[3] YARAMASU V, WU B, SEN P C, et al. High-power wind energy conversion systems: state-of-the-art and emerging technologies[J]. Proceedings of the IEEE, 2015, 103(5): 740-788.

[4] 王淑云, 娄素华, 刘文霞, 等. 考虑火电深度调峰的电力系统低碳发电优化研究[J]. 全球能源互联网, 2019, 2(3): 226-231.

WANG Shuyun, LOU Suhua, LIU Wenxia, et al. Research on optimization of low carbon generation in power system considering thermal power depth peak-modulation[J].Journal of Global Energy Interconnection, 2019, 2(3): 226-231.

[5] 苏康博, 杨洪明, 余千, 等. 考虑多类型水电协调的风光电站容量优化配置方法[J]. 电力系统保护与制, 2020, 48(4): 80-88.

SU Kangbo, YANG Hongming, YU Qian, et al. Optimal capacity configuration method of wind-solar power station considering the coordination of multi-type hydropower[J]. Power System Protection and Control, 2020, 48(4): 80-88.

[6] LI J, WANG S, YE L, et al. A coordinated dispatch method with pumped-storage and battery-storage for compensating the variation of wind power[J]. Protection and Control of Modern Power Systems, 2018, 3(1): 21-34.

[7] 崔杨, 杨志文, 严干贵, 等. 降低火电机组调峰成本的光热电站储热容量配置方法[J]. 中国电机工程学报, 2018, 38(6): 1605-1611, 1896.

CUI Yang, YANG Zhiwen, YAN Gangui, et al. Capacity configuration of thermal energy storage within CSP to reduce the cost of peak load regulation[J]. Proceedings of the CSEE, 2018, 38(6): 1605-1611, 1896.

[8] 林俐, 岳晓宇, 许冰倩, 等. 计及抽水蓄能和火电深度调峰效益的抽蓄–火电联合调峰调用顺序及策略[J]. 电网技术, 2021, 45(1): 20-32.

LIN Li, YUE Xiaoyu, XU Bingqian, et al. Call sequence and strategy of combined peaking of pumped storage and thermal power considering the benefit of pumped storage and thermal power depth peaking[J]. Power System Technology, 2021, 45(1): 20-32.

[9] 李星梅, 钟志鸣, 阎洁. 大规模风电接入下的火电机灵活性改造规划[J]. 电力系统自动化, 2019, 43(3): 51-57.

LI Xingmei, ZHONG Zhiming, YAN Jie. Flexibility reformation planning of thermal power units with large-scale integration of wind power[J]. Automation of Electric Power Systems, 2019, 43(3): 51-57.

[10] 叶泽, 李湘旗, 姜飞, 等. 考虑最优弃能率的风光火储联合系统分层优化经济调度[J]. 电网技术, 2021, 45(6): 2270-2280.

YE Ze, LI Xiangqi, JIANG Fei, et al. Hierarchical optimization economic dispatching of combined wind-PV-thermal-energy storage system considering the optimal energy abandonment rate[J]. Power System Technology, 2021, 45(6): 2270-2280.

[11] 帅挽澜, 朱自伟, 李雪萌, 等. 考虑风电消纳的综合能源系统“源-网-荷-储”协同优化运行[J]. 电力系统保护与控制, 2021, 49(19): 18-26.

SHUAI Wanlan, ZHU Ziwei, LI Xuemeng, et al. “Source-network-load-storage” coordinated optimization operation for an integrated energy system considering wind power consumption[J]. Power System Protection and Control, 2021, 49(19): 18-26.

[12] 王耀华, 栗楠, 元博, 等. 含大比例新能源的电力系统规划中“合理弃能”问题探讨[J]. 中国电力, 2017, 50(11): 8-14.

WANG Yaohua, LI Nan, YUAN Bo, et al. Discussion on the reasonable curtailment problems in highly renewable power system planning[J]. Electric Power, 2017, 50(11): 8-14.

[13] KUBIK M L, COKER P J, BARLOW J F. Increasing thermal plant flexibility in a high renewables power system[J]. Applied Energy, 2015, 154: 102-111.

[14] ENERGIEWENDE A. Flexibility in thermal power plants-with a focus on existing coal-fired power plants[R]. Berlin, Germany: Energiewende A, 2017.

[15] 王金星, 卓建坤, 李菁, 等. 适应燃煤电厂灵活调峰的安全改造技术探讨[C] // 2018火电灵活性改造及深度调峰技术交流研讨会论文集, 2018年3月28日, 中国, 沈阳: 24-30.

WANG Jinxing, ZHUO Jiankun, LI Jing, et al. Discussion on safety retrofit technology for flexible peak regulation of coal-fired power plants[C] // 2018 Workshop on Flexible Retrofit and Deep Peak Regulation Technology of Thermal Power Plants, March 28, 2018, Shenyang, China: 24-30.

[16] VENKATARAMAN S, JORDAN G, O’CONNOR M. Cost-benefit analysis of flexibility retrofits for coal and gas-fueled power plants[R]. NREL, U.S. Department of Energy, 2013.

[17] GARBRECHT O, BIEBER M, KNEER R. Increasing fossil power plant flexibility by integrating molten-salt thermal storage[J]. Energy, 2017, 118(1): 876-883.

[18] DESCUES T, RUER J, MARTY P, et al. A thermal energy storage process for large scale electric applications[J]. Applied Thermal Engineering, 2010, 30(5): 425-432.

[19] ZHAO Y L, WANG C Y, LIU M, et al. Improving operational flexibility by regulating extraction steam of high-pressure heaters on a 660 MW supercritical coal-fired power plant: a dynamic simulation[J]. Applied Energy, 2018, 212: 1295-1309.

[20] 杨寅平, 曾沅, 秦超, 等. 面向深度调峰的火电机组灵活性改造规划模型[J]. 电力系统自动化, 2021, 45(17): 79-88.

YANG Yinping, ZENG Yuan, QIN Chao, et al. Flexible transformation planning model of thermal power unit for deep peaking[J]. Automation of Electric Power Systems, 2021, 45(17): 79-88.

[21] 彭元, 娄素华, 范越, 等. 考虑火电机组储热改造的电力系统低碳经济调度[J]. 电网技术, 2020, 44(9): 3339-3345.

PENG Yuan, LOU Suhua, FAN Yue, et al. Low-carbon economical dispatch of power system onsidering thermal energy storage in thermal power units[J]. Power System Technology, 2020, 44(9): 3339-3345.

[22] 何洋, 胡军峰, 闫志涛, 等. 大规模风电入网辅助服务成本补偿机制研究[J]. 电网技术, 2013, 37(12): 3552-3557.

HE Yang, HU Junfeng, YAN Zhitao, et al. Compensation mechanism for ancillary service cost of grid-integration of large-scale wind farms[J]. Power System Technology, 2013, 37(12): 3552-3557.

[23] 向红吉, 戴朝华, 明杰, 等. 考虑低谷时刻负调峰能力及风电预测区间的多目标机组组合优化研究[J]. 电网技术, 2017, 41(6): 1912-1918.

XIANG Hongji, DAI Chaohua, MING Jie, et al. Research on multi-objective optimization of unit commitment considering negative peak load regulation ability in valley load period and wind power prediction interval[J]. Power System Technology, 2017, 41(6): 1912-1918.

[24] 秦婷, 刘怀东, 王锦桥, 等. 基于碳交易的电-热-气综合能源系统低碳经济调度[J]. 电力系统自动化, 2018, 42(14): 8-13.

QIN Ting, LIU Huaidong, WANG Jinqiao, et al. Carbon trading based low-carbon economic dispatch for integrated electricity-heat-gas energy system[J]. Automation of Electric Power Systems, 2018, 42(14): 8-13.

[25] 国家发改委. 全国碳交易市场的配额分配方案(讨论稿)[EB/OL].[2017-06-02].http://www.cnenergynews.cn/hb/tpf/201706/t20170602_444547.html

[26] 中华人民共和国环境保护税法实施条例[N]. 中国环境报, 2018-01-01(002).

[27] 国家发展改革委. 国家能源局网站.《清洁能源消纳行动计划(2018-2020 年)》[EB/OL]. [2018-10-30].https://www.ndrc.gov.cn/xxgk/zcfb/ghxwj/201812/W020190905495739358481.pdf.

Low-carbon economic scheduling of solar thermal storage considering heat storage transformation and optimal energy abandonment

ZANG Zikun, YANG Xiaohui, LI Zhaohui, YUAN Zhixin, XU Chao, CHEN Suhao

(School of Information Engineering, Nanchang University, Nanchang 330031, China)

Large-scale renewable energy consumption and low carbon development of power systems have a higher need to reduce carbon emissions in the peak frequency modulation of thermal power units. To improve the economical efficiency of the system and the low carbon of the thermal motor peak adjustment, this paper proposes a hierarchical optimal scheduling method of the thermal storage considering the thermal power unit's heat storage transformation and optimal solar energy abandonment. Considering the reverse peak adjustment characteristics of wind, an optimal energy-discarding constraint model is established, and an upper model is constructed to minimize the net load variance of the power grid. The net load curve is "peak-clipping". To expand the peak-shaving depth of thermal power units, a carbon transaction cost model is established considering the transformation of heat storage units. From this, the lower layer model is established with the goal of minimizing the total system cost and carbon transaction cost. A collaborative optimization of system economy and low carbon is realized while the net load curve is "peak-cutting and valley filling" twice. The rationality and validity of the proposed model are verified by an example.

thermal power unit heat storage transformation; optimal energy abandonment rate; carbon trading; peak cutting and valley filling; layered optimization

10.19783/j.cnki.pspc.211405

2021-10-19；

2022-03-24

臧紫坤(1997—),男，硕士研究生，主要研究方向为电力系统运行优化、新能源消纳等；E-mail: 2767140767@ qq.com

杨晓辉(1978—)，男，通信作者，博士、教授、博导，研究方向为新能源并网优化、电力电子在新能源中的应用。E-mail: yangxiaohui@ncu.edu.cn

国家自然科学基金项目资助(51765042, 61773051，61963026)；江西省研究生创新专项项目资助(YC2021-S153)

This work is supported by the National Natural Science Foundation of China (No. 51765042, No. 61773051, and No. 61963026).

(编辑 葛艳娜)