基于电流一致性的直流微网自适应下垂控制

曾 浩，赵恩盛，周思宇，韩 杨，杨 平，王丛岭

基于电流一致性的直流微网自适应下垂控制

曾 浩，赵恩盛，周思宇，韩 杨，杨 平，王丛岭

(电子科技大学机械与电气工程学院，四川 成都 611731)

在直流微电网中，传统下垂控制存在功率均分和母线电压控制不能同时兼顾的矛盾。针对这一问题，研究了带阻性负载直流微网系统，提出基于电流一致性的直流微网自适应下垂控制策略。该策略包括一次、二次和电流一致性控制。引入输出电容电压反馈构成一次控制，参考电压补偿和下垂系数修正构成二次控制。各分布式电源间仅相邻变换器交换电流信息，通过电流一致性迭代控制和一次、二次控制结合，在保障输出功率均分的同时，消除了直流母线电压偏差。为验证该策略的控制有效性，对系统进行小信号建模理论分析，分析控制参数变化对系统稳定性的影响，最后进行了仿真验证。理论分析与仿真结果表明，该控制策略在微网结构改变时，也能保证系统稳定，自适应完成直流微网功率均分和母线电压控制目标。

直流微网；电流一致性；自适应下垂控制；母线电压控制；功率均分

0 引言

近年来，直流微电网因其可靠性、可扩展性和高效性等特点而受到广泛关注。相比交流微电网，直流微电网具有诸多优点，能够有效地接入光伏、储能和燃料电池等本质上具有直流特性的分布式电源，且不需要考虑相位、频率和无功等问题，控制相对简单，具有广泛的应用前景[1-7]。

在直流微电网的控制中，传统下垂控制存在母线电压稳态误差[8]，可以采用补偿法进行改进[9]。文献[10]在传统下垂控制的基础上，设计了具有下垂系数自适应调节补偿的控制器，在一定程度上改善了下垂控制的固有矛盾。文献[11]提出一种带母线电压多级前馈补偿的直流微网分段线性下垂控制策略，通过设置下垂系数和进行母线电压多级前馈补偿，解决了均流与母线电压跌落问题。文献[12]针对传统下垂控制存在的随着电荷状态(State of Charge, SOC)减小，母线电压跌落的问题，提出一种基于SOC的改进下垂控制策略。文献[13]提出一种限流下垂控制方法，改善了功率均分效果。这些研究针对下垂控制的固有矛盾从不同方面提出了改进策略，在一定程度上改善了母线电压控制和功率均分控制。但是，这些控制方法多以集中式控制器为主，对通信依赖度高，系统稳定性难以保证。

除了采用补偿法改进下垂控制外，一致性控制因具有高效率、高容错性、内在的并行性[14-17]和降低通信成本[18]等优点，已受到较多学者关注，一致性控制在通信结构变化的情况下仍能实现相应控制目的[19]。文献[20]提出一种基于一致性算法的改进下垂控制策略，该策略利用相邻变换器信息，减少了通信量，实现了无功功率的精确分配，但是该方法适用于交流系统，并且未考虑控制参数对系统稳定性的影响。文献[21]提出一种基于多代理一致性的能量动态协调与功率精确控制策略，可以有效地协调功率的精确控制与底层的自治运行。文献[22]在混合多端直流每个端子设置一个代理构成多代理系统，用一致性算法实现自律分散控制，进行系统的损耗优化，显著降低了混合多端直流损耗。文献[23]提出一种受通信故障和通信延迟影响较小的分布式多光伏功率协调控制策略，保证功率均衡，且均衡了光伏间负荷分配。文献[24]提出一种基于离散一致性的自适应下垂控制策略，实现了变虚拟电阻的自适应下垂控制，增加了控制的鲁棒性及灵活性。这些有关直流微网系统控制策略的研究，虽然采用了以分布式控制器为主的一致性算法，但是缺乏控制参数对系统稳定性影响的讨论。

本文在现有下垂控制和一致性控制研究的基础上，提出了基于电流一致性的直流微网自适应下垂控制。所提出的控制策略适用于低压直流微电网，比如某些数据和电信设备直流系统[25]。控制策略包含一次控制、二次控制和电流一致性控制，利用输出电容电压和电感电流反馈得到的参考电压补偿和下垂系数修正构成二次控制，二次控制的输出作为一次控制的输入。各变换器仅交换相邻电流信息，通过电流一致性迭代控制和一次、二次控制结合，在保障功率均分的前提下，消除了直流母线电压偏差。此外，当微网结构改变时，系统还能保持稳定，自适应地维持母线电压和均分输出功率。最后，通过理论分析和PLECS仿真验证了所提控制策略的有效性。

1 传统下垂控制

图1 双BOOST变换器并联等效电路

由图1的等效电路，根据回路电压方程得到直流微电网等效电路的电压电流下垂特性表达式为

由式(3)可以看出，增大下垂系数K，变换器输出电流差值会减小，功率均分效果改善，但是母线电压偏差更大。由此说明，传统下垂控制可以在一定程度上提高功率均分效果，但是也会降低母线电压控制精度，这种控制并不能同时兼顾母线电压控制和功率均分控制。

2 基于电流一致性自适应下垂控制

2.1 电流一致性迭代

传统离散一致性控制公式描述为[26]

本文采用的电流一致性迭代算法在上述式(4)的基础上进行改进，确保了在动态环境改变下的一致性收敛[27]。

2.2 电流一致性自适应下垂控制

在传统下垂控制的基础上改进，把双变换器推广到多变换器控制结构，在一次控制和二次控制的基础上，引入电流一致性算法，构成基于电流一致性的直流微网自适应下垂控制策略。

此时微网下垂特性表达式为

图4 直流微网电流一致性自适应控制结构

此时参考电压补偿量的大小满足：

图5 自适应下垂特性曲线

由此说明，相比传统下垂控制，所提出的控制方法经过一次控制、二次控制和一致性算法结合得到下垂系数修正量和参考电压补偿量后，能在保障功率均分的同时保障母线电压控制，恢复母线电压。

3 稳定性分析

为了研究所提出控制策略对系统稳定性的影响及其参数选择依据，对图4所示的直流系统在稳态工作点附近进行局部线性化小信号建模分析。

由图4的控制结构可知，一致性算法提供各变换器参考电流值，然后经过二次控制得到下垂系数修正量和参考电压补偿量，最后经过一次控制得以实现控制目标。图4的控制结构可以表示为图6所示传递函数框图。

图6 电流一致性自适应控制框图

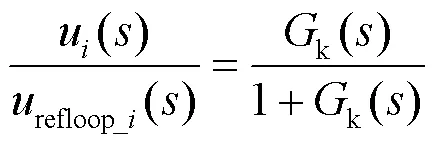
在图1的电路结构中，有如下关系：

对系统进行小信号分析，加入小扰动，求解母线电压扰动与电压参考值小扰动之间的关系。大写字母表示稳态值，上小三角标表示小扰动，得到：

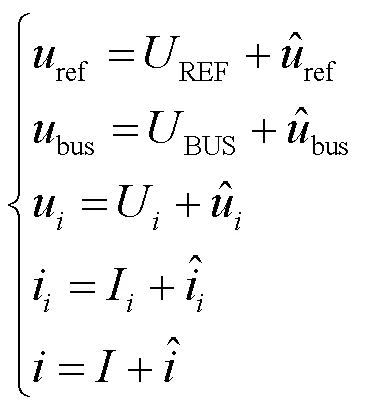
其中，稳态关系有

由式(16)、式(17)得到小信号表示：

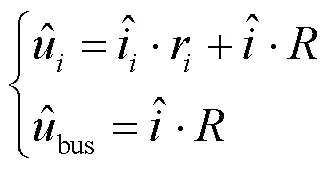
令式(11)满足下式：

由式(6)、式(10)—式(20)可得到：

其中：

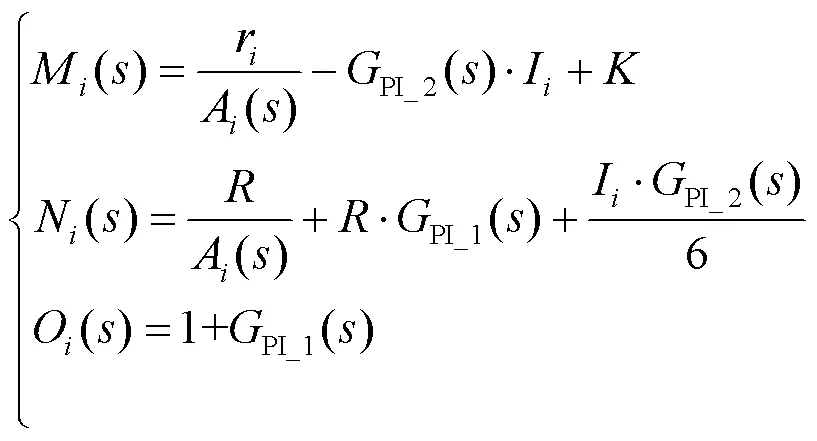
由式(10)—式(22)得到：

式(23)表示了母线电压扰动与电压参考值小扰动的传递函数关系。根据式(23)，按照表1系统参数设置传递函数，得到的系统闭环传递函数零极点分布，如图7所示。

图7中，系统的零极点分布划分为两部分，第一部分对系统性能的影响较小，离原点较远。第二部分靠近原点，对系统性能影响较大，称为主导极点。图7表示系统所有零极点分布于S平面左半平面，所以系统稳定。由此说明所提出的控制策略能保证系统稳定。

图7表明系统在表1所选取的参数下具有稳定性，但是各PI控制器参数变化对系统的影响还不能明确。在表1的基础上，选择合适的参数范围，分析三个PI控制器参数和系统负载参数对系统稳定性的影响。

表1 系统参数

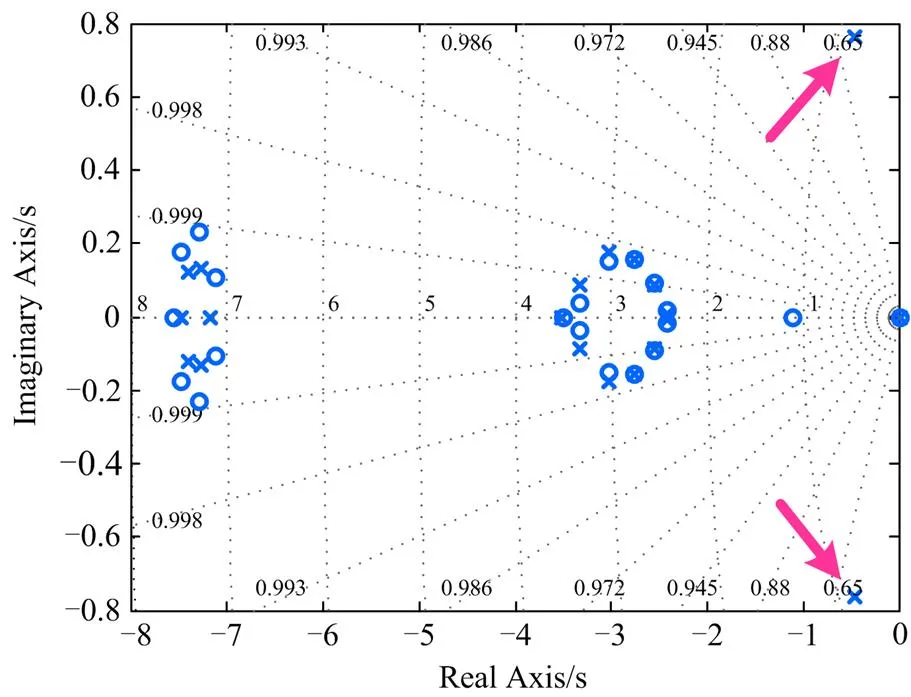
图7 系统零极点分布

图8表示系统在保持其余参数不变的情况下，只改变1号PI控制器的比例、积分项参数时的主导极点分布变化趋势图。图8(a)中，当比例系数从0增大到1.8，每次递增0.1时，主导极点向实轴靠近，系统阻尼逐渐增大，调节时间变小，超调量也逐渐减小。

图8 第一 PI控制器参数变化主导极点变化趋势

Fig. 8 The first PI controller parameter changes dominate the pole change trend

图8(b)中，积分系数从0增大到4.2，每次递增0.3，一对共轭主导极点逐渐远离实轴，系统阻尼逐渐减小，调节时间变大，超调量逐渐增大。第一PI控制器比例积分系数变化过程中，极点分布始终保持在S平面左半平面，系统保持稳定。

图9为系统在保持其余参数不变的情况下，改变2号PI控制器比例系数和积分系数的主导极点分布变化趋势图。图9(a)中，比例系数从0增大到0.24，每次递增0.01，图中一对靠近虚轴的共轭主导极点位置基本保持不变，原先分布于实轴的极点缓慢向原点靠近。在比例系数的增加过程中，系统传递函数零极点始终保持在S平面左半平面，系统保持稳定。图9(b)中，积分系数从0增大到1，每次递增0.1，一对共轭主导极点位置基本保持不变，原先分布于实轴的零极点向原点靠近，随着第二PI控制器积分系数的增加，系统极点分布扩散到S平面右半平面，并且向着远离虚轴的方向移动，系统变得不稳定。

图9 第二 PI控制器参数变化主导极点变化趋势

Fig. 9 The second PI controller parameter changes dominate the pole change trend

对于整个系统，2号PI控制器在比例系数的变化下能保持稳定，但积分系数的增大会导致系统稳定性下降。

图10为系统在保持其余参数不变的情况下，改变3号PI控制器比例系数和积分系数的主导极点分布变化趋势图。图10(a)中，比例系数从0增大到0.06，每次递增0.005，图中靠近虚轴的一对主导极点逐渐下移靠近实轴，原先分布于实轴的零极点逐渐靠近原点，系统阻尼逐渐增大，调节时间变小，超调量也逐渐减小。

图10 第三PI控制器参数变化主导极点变化趋势

Fig. 10 The third PI controller parameter changes dominate the pole change trend

图10(b)中，积分系数从0增大到0.44，每次递增0.044。图中一对主导极点逐渐远离实轴，原先分布于实轴附近的零极点逐渐远离原点，系统阻尼减小，调节时间变大，超调量也逐渐增大。在第三PI参数变化的整个过程中，零极点始终保持在S平面左半平面，系统保持稳定。

图11为系统在保持其余参数不变的情况下，改变阻性负载的大小时的极点分布变化趋势图。阻性负载逐渐加重，阻值从10 Ω减小到5 Ω，每次递减1 Ω，负载功率由16 kW逐渐加重到32 kW。图11中一对共轭主导极点逐渐靠近实轴，系统阻尼逐渐增大，调节时间变小，超调量也逐渐减小，系统极点分布始终保持在S平面左半平面，系统保持稳定。

图11 阻性负载变化主导极点变化趋势

4 仿真分析

为了验证所提出控制策略有效性，在PLECS软件仿真平台搭建图4所示结构的直流微网进行多工况仿真测试。仿真模型中的通信拓扑采用图3所示交叉通信拓扑。

在PLECS仿真中，6个BOOST直流变换器的电路参数选取与表1系统参数一致，常数权重取2/9，得到仿真结果：

考虑负载跳变情况，如图12所示。直流母线上阻性负载在10 Ω和5 Ω之间跳变，负载功率由16 kW变为32 kW，最后变回16 kW。图4中开关SwitchR闭合负载加重时，母线电压电压降约7.5%，超调量2.5%，经过约0.4 s调整回参考电压值400 V，稳态误差为0。负载减轻时，母线电压电压上升8.25%，经过约0.4 s调节时间，稳态误差为0。如图13所示，负载跳变后，输出电流变得不一致，经过约0.36 s调整后，各变换器输出电流重新收敛。

图12 负载跳变母线电压波形

图13 负载跳变输出电流波形

图14表示在图12和图13的负载工况下，6个变换器各自的参考电压补偿量及下垂系数修正量波形。图14证明了公式(9)的正确性，以负载加重后#1变换器为例。从图14中得到数据，下垂系数修正量-0.73，表1中#1变换器输出线路阻抗取1 Ω、下垂系数取15，输出电流从图13得到约为13.6 A，按照公式(9)计算得到参考电压补偿量207.67。在排除读数误差后，仿真结果符合理论分析。

图14 负载跳变时电压补偿量及下垂系数修正量波形

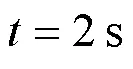
图17表示在#4变换器脱机工况下，6个变换器各自的参考电压补偿量及下垂系数修正量波形。与图14分析同理，在排除读数误差后，仿真结果符合理论分析，满足公式(9)。

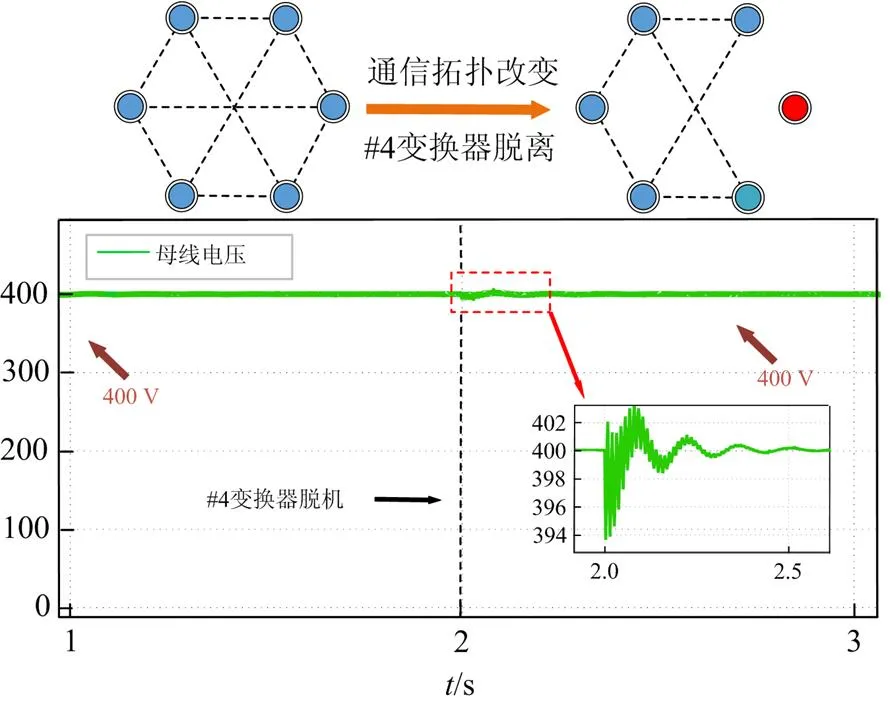
图15 #4变换器脱离母线电压波形

图16 #4变换器脱离时输出电流波形

图17 #4变换器脱离时电压补偿及下垂系数修正波形

仿真结果表明所提出的控制策略能够很好地适应负载突变和变换器脱机复杂工况。当微网结构改变时，控制策略无需改变，母线电压经过一定的调节时间能很快达到零稳态误差。各变换器输出电流也能很快重新达到一致，实现功率均分。

5 结论

本文针对传统下垂控制和集中式控制局限性，提出了基于电流一致性的直流微电网自适应下垂控制策略。

1) 分析了传统下垂控制的局限性，传统下垂控制能在一定程度上提高功率均分效果，但这种控制并不能同时兼顾母线电压控制和功率均分控制。

2) 通过提出的自适应控制策略进行参考电压补偿、下垂系数修正，在微网结构改变等工况下也能达到准确的功率均分和母线电压控制。

3) 分析了各控制参数变化对系统的影响。最后通过仿真证明所提控制策略具有良好控制效果，系统能保持稳定，适应复杂工况，经过一定的调节时间，母线电压能达到稳态误差为零且功率重新均衡。

[1] 孟欣, 王丹, 张子阳, 等. 面向电能交易的用户级直流微网母线电压分层控制策略研究[J]. 电力系统保护与控制, 2021, 49(4): 54-63.

MENG Xin, WANG Dan, ZHANG Ziyang, et al. Research on hierarchical control strategy of a user level DC microgrid bus voltage for electricity trading[J]. Power System Protection and Control, 2021, 49(4): 54-63.

[2] 温家良, 吴锐, 彭畅, 等. 直流电网在中国的应用前景分析[J]. 中国电机工程学报, 2012, 32(13): 7-12.

WEN Jialiang, WU Rui, PENG Chang, et al. Analysis of DC grid prospects in China[J]. Proceedings of the CSEE, 2012, 32(13): 7-12.

[3] 李霞林, 郭力, 王成山, 等. 直流微电网关键技术研究综述[J]. 中国电机工程学报, 2016, 36(1): 2-17.

LI Xialin, GUO Li, WANG Chengshan, et al. Key technologies of DC microgrids: an overview[J]. Proceedings of the CSEE, 2016, 36(1): 2-17.

[4] 杜祥伟, 沈艳霞, 李静. 基于模型预测控制的直流微网混合储能能量管理策略[J]. 电力系统保护与控制, 2020, 48(16): 69-75.

DU Xiangwei, SHEN Yanxia, LI Jing. Energy management strategy of DC microgrid hybrid energy storage based on model predictive control[J]. Power System Protection and Control, 2020, 48(16): 69-75.

[5] MENG Xin, ZHU Yanbin, LIU Lei, et al. Research on power control strategy of household-level electric power router based on hybrid energy storage droop control[J]. Protection and Control of Modern Power Systems, 2021, 6(2): 178-190.

[6] 张天翼, 郑凯元, 王海风. 聚合相同分布式电源对直流微电网高频振荡稳定性的影响[J]. 中国电力, 2021, 54(8): 103-108.

ZHANG Tianyi, ZHENG Kaiyuan, WANG Haifeng. Impact of large number of same aggregated distributed generators on the high-frequency oscillatory stability of a DC microgrids[J]. Electric Power, 2021, 54(8): 103-108.

[7] 余雪莹, 李华强, 杨龙杰, 等. 兼顾企业综合成本与用户用电体验的微电网双层优化配置[J]. 电力科学与技术学报, 2020, 35(2): 38-45.

YU Xueying, LI Huaqiang, YANG Longjie, et al. Bi-level programming method for optimal sizing of grid-connected DC microgrid system based on economic efficiency of enterprises and customer electricity experience[J]. Journal of Electric Power Science and Technology, 2020, 35(2): 38-45.

[8] 孙石涛, 王久和. 直流微网混合无源控制及系统分层控制策略[J]. 电力系统及其自动化学报, 2021, 33(6): 35-41.

SUN Shitao, WANG Jiuhe. Hybrid passivity-based control of DC microgrid and hierarchical control strategy for system[J]. Proceedings of the CSU-EPSA, 2021, 33(6): 35-41.

[9] 朱珊珊, 汪飞, 郭慧, 等. 直流微电网下垂控制技术研究综述[J]. 中国电机工程学报, 2018, 38(1): 72-84, 344.

ZHU Shanshan, WANG Fei, GUO Hui, et al. Overview of droop control in DC microgrid[J]. Proceedings of the CSEE, 2018, 38(1): 72-84, 344.

[10] 郑永伟, 陈民铀, 李闯, 等. 自适应调节下垂系数的微电网控制策略[J]. 电力系统自动化, 2013, 37(7): 6-11.

ZHENG Yongwei, CHEN Minyou, LI Chuang, et al. A microgrid control strategy based on adaptive drooping coefficient adjustment[J]. Automation of Electric Power Systems, 2013, 37(7): 6-11.

[11] 刘宿城, 吴亚伟, 李中鹏, 等. 带母线电压多级补偿的直流微网下垂控制策略[J]. 电子科技大学学报, 2020, 49(2): 248-254.

LIU Sucheng, WU Yawei, LI Zhongpeng, et al. Droop control strategy with bus multi-level compensation for DC microgrid[J]. Journal of University of Electronic Science and Technology of China, 2020, 49(2): 248-254.

[12] 袁娜娜, 王允建, 张君, 等. 直流微网中基于SOC的改进下垂控制[J]. 电力系统保护与控制, 2019, 47(15): 17-23.

YUAN Nana, WANG Yunjian, ZHANG Jun, et al. Improved droop control based on SOC in DC microgrid[J]. Power System Protection and Control, 2019, 47(15): 17-23.

[13] BRAITOR A C, KONSTANTOPOULOS G C, KADIRKAMANATHAN V. Current-limiting droop control design and stability analysis for paralleled boost converters in DC microgrids[J]. IEEE Transactions on Control Systems Technology, 2021, 29(1): 385-394.

[14] 周烨, 汪可友, 李国杰, 等. 基于多智能体一致性算法的微电网分布式分层控制策略[J]. 电力系统自动化, 2017, 41(11): 142-149.

ZHOU Ye, WANG Keyou, LI Guojie, et al. Distributed hierarchical control for microgrid based on multi-agent consensus algorithm[J]. Automation of Electric Power Systems, 2017, 41(11): 142-149.

[15] 王岳, 杨国华, 董晓宁, 等. 基于多智能体一致性的微电网无功功率分配方法研究[J]. 电力系统保护与控制, 2019, 47(17): 54-60.

WANG Yue, YANG Guohua, DONG Xiaoning, et al. Study on reactive power distribution method of microgrid based on multi-agent consistency[J]. Power System Protection and Control, 2019, 47(17): 54-60.

[16] 梁海峰, 丁锦睿, 边吉. 考虑通信延时的直流微网分组一致性控制策略研究[J]. 华北电力大学学报(自然科学版), 2021, 48(2): 20-29, 39.

LIANG Haifeng, DING Jinrui, BIAN Ji. Research on control strategy of DC microgrids based on group consensus algorithm considering communication delay[J]. Journal of North China Electric Power University (Natural Science Edition), 2021, 48(2): 20-29, 39.

[17] SAMENDE C, BHAGAVATHY S M, MCCULLOCH M. Power loss minimisation of off-grid solar DC nano-grids—part II: a quasi-consensus-based distributed control algorithm[J]. IEEE Transactions on Smart Grid, 2022, 13(1): 38-46.

[18] CHEN Z, YU X, XU W, et al. Modeling and control of islanded DC microgrid clusters with hierarchical event-triggered consensus algorithm[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2021, 68(1): 376-386.

[19] 李一琳, 董萍, 刘明波, 等. 基于有限时间一致性的直流微电网分布式协调控制[J]. 电力系统自动化, 2018, 42(16): 96-103.

LI Yilin, DONG Ping, LIU Mingbo, et al. Distributed coordinated control of DC microgrid based on finite-time consensus algorithm[J]. Automation of Electric Power Systems, 2018, 42(16): 96-103.

[20] 张莹, 孟润泉, 王子昂, 等. 一种基于一致性算法的改进下垂控制策略[J]. 电力系统保护与控制, 2021, 49(14): 104-111.

ZHANG Ying, MENG Runquan, WANG Ziang, et al. An improved droop control strategy based on a consensus algorithm[J]. Power System Protection and Control, 2021, 49(14): 104-111.

[21] 郝然, 艾芊, 朱宇超. 基于多智能体一致性的能源互联网协同优化控制[J]. 电力系统自动化, 2017, 41(15): 10-17, 57.

HAO Ran, AI Qian, ZHU Yuchao. Cooperation optimal control of energy internet based on multi-agent consistency[J]. Automation of Electric Power Systems, 2017, 41(15): 10-17, 57.

[22] 韩民晓, 许冬, 万磊. 基于一致性算法的混合多端直流自律分散控制[J]. 电力系统自动化, 2016, 40(12): 130-136.

HAN Minxiao, XU Dong, WAN Lei. Consensus algorithm based decentralized autonomous control of hybrid multi-terminal direct current system[J]. Automation of Electric Power Systems, 2016, 40(12): 130-136.

[23] 汤茂东, 曲小慧, 姚若玉, 等. 基于离散一致性算法的直流配电网多光伏协调控制策略[J]. 电力系统自动化, 2020, 44(24): 89-95.

TANG Maodong, QU Xiaohui, YAO Ruoyu, et al. Multi-photovoltaic coordinated control strategy in DC distribution network based on discrete consensus algorithm[J]. Automation of Electric Power Systems, 2020, 44(24): 89-95.

[24] 吕振宇, 吴在军, 窦晓波, 等. 基于离散一致性的孤立直流微网自适应下垂控制[J]. 中国电机工程学报, 2015, 35(17): 4397-4407.

LÜ Zhenyu, WU Zaijun, DOU Xiaobo, et al. An adaptive droop control for the islanded DC microgrid based on discrete consensus algorithm[J]. Proceedings of the CSEE, 2015, 35(17): 4397-4407.

[25] 刘彦呈, 庄绪州, 张勤进, 等. 基于虚拟频率的直流微电网下垂控制策略[J]. 电工技术学报, 2021, 36(8): 1693-1702.

LIU Yancheng, ZHUANG Xuzhou, ZHANG Qinjin, et al. A virtual current-frequency droop control in DC microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1693-1702.

[26] OLFATI-SABER R, FAX J A, MURRAY R M. Consensus and cooperation in networked multi-agent systems[J]. Proceedings of the IEEE, 2007, 95(1): 215-233.

[27] MENG L, DRAGICEVIC T, ROLDAN-PEREZ J, et al. Modeling and sensitivity study of consensus algorithm-based distributed hierarchical control for DC microgrids[J]. IEEE Transactions on Smart Grid, 2016, 7(3): 1504-1515.

[28] 林成嘉. 直流微电网协调控制策略及实验研究[D]. 成都: 电子科技大学, 2018.

LIN Chengjia. Coordinated control strategy and experimental research of DC micro grid[D]. Chengdu: University of Electronic Science and Technology of China, 2018.

Adaptive droop control of a DC microgrid based on current consistency

ZENG Hao, ZHAO Ensheng, ZHOU Siyu, HAN Yang, YANG Ping, WANG Congling

(School of Mechanical and Electrical Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China)

In a DC microgrid, conventional droop control has the contradiction that power sharing and bus voltage control cannot be considered at the same time. To solve this problem, a system with resistive load is studied, and adaptive droop control of the DC microgrid based on current consistency strategy is proposed. The strategy includes primary, secondary and current consistency control. The introduction of output capacitor voltage feedback constitutes the primary control, and reference voltage compensation and droop coefficient correction constitute the secondary control. Each distributed power supply only exchanges current information between adjacent converters. Through the iterative control of current consistency and the combination of primary and secondary control, the bus voltage deviation is eliminated while ensuring the output power is evenly divided. In order to verify the control effectiveness of the strategy, small-signal modeling theory of the system is analyzed, and the influence of the change of control parameters on the stability of the system is analyzed. Finally, simulation verification is carried out. Theoretical analysis and simulation results show that the proposed control strategy can also ensure the stability of the system when the structure of DC microgrid changes, and achieve the goal of power sharing and bus voltage control adaptively.

DC microgrid; current consistency; adaptive droop control; bus voltage control; power sharing

10.19783/j.cnki.pspc.211404

2021-10-19；

2022-02-07

曾 浩(1998—)，男，硕士研究生，研究方向为直流微电网控制稳定性、电能质量；E-mail:HaoZeng2020@163.com

赵恩盛(1990—)，男，博士研究生，研究方向为微电网稳定性分析及其协调控制技术；E-mail:zhaoens@163.com

韩 杨(1982—)，男，通信作者，博士，教授，研究方向为电力系统运行与控制、电能质量。E-mail: hanyang@ uestc.edu.cn

国家自然科学基金项目资助(51977026)；四川省科技计划资助(2021YFG0255)

This work is supported by the National Natural Science Foundation of China (No. 51977026).

(编辑 葛艳娜)