基于秃鹰算法的PID参数自整定*
2022-06-16任宇希丁振伟莫愁覃柄涪肖浩彬
任宇希,丁振伟,莫愁,覃柄涪,肖浩彬
(1.桂林电子科技大学 541004;2.桂林智工科技有限责任公司 541001)
随着计算机技术的发展,PID控制因其简单、方便的优势,被广泛应用于电子、自动控制、航天等领域[1-2],在工程控制领域有着十分重要的地位,在实际系统中所占比例超过90%[3]。对于PID控制,最为关键的就是PID的参数整定,常规的参数整定方法,比较复杂难以实现,而且多存在震荡的情况。使用智能算法能有效快速地实现PID参数整定。文献[4]提出了蝙蝠算法的PID参数整定,分别使用Ziegler-Nichols方法、粒子群算法和蝙蝠算法获得PID参数,对比了三种方法的系统闭环性能和运行效率。
1 秃鹰算法
秃鹰搜索(bald eagle search,BES)优化是马来西亚学者Alsattar于2020年提出的一种新型元启发式算法,该算法具有较强的全局搜索能力,能够有效地解决各类复杂数值优化问题的优点[5]。其算法原理如下:
秃鹰是一种遍布于北美洲地区的猛禽,飞行中视力敏锐,观察能力优秀.以其捕食鲑鱼为例,首先秃鹰会基于个体和种群到鲑鱼的浓度来选择搜索空间,朝一个特定区域飞行;其次在选定搜索空间内搜索水面,直到发现合适的猎物;最后秃鹰会逐渐改变飞行高度,快速向下俯冲,从水中成功捕获鲑鱼等猎物。BES算法以秃鹰捕食猎物的行为进行模拟,将其分为选择搜索空间、搜索空间猎物和俯冲捕获猎物三个阶段。
2 秃鹰算法的PID参数整定
2.1 PID控制原理
在控制系统中,PID控制的应用十分广泛,传统的PID控制一般是由控制器和受控对象所组成,是一种线性的控制系统。
PID 参数优化的目的在于寻找一组 Kp、Ki、Kd,使系统的指标达到最优。
r(t)为系统的输入,y(t)为系统的输出,e(t)为系统的偏差,u(t)为PID控制器的输出,故存在以下表达式:

PID控制的标准函数公式如下:
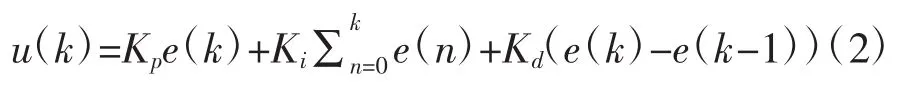
经过标准简化的传递函数模型如下:

K为控制器增益,Ti为积分时间常数,Td为微分时间常数。


2.2 目标函数
影响系统性能的指标有很多,单位阶跃信号和稳态误差分别用来衡量闭环系统的动态性能和稳态性能,我们所指的动态性能一般包括上升时间tr、峰值时间 tp、超调量 σ、调节时间 ts、震荡次数N。使用秃鹰算法进行PID参数优化,每只秃鹰都可以分别作为Kp(比例)、Ki(积分)、Kd(微分)三个参数,在搜索空间内,令 Kp∈[kpmin,kpmax],Ki∈[kimin,kimax],Kd∈[kdmin,kdmax],对种群进行初始化、适应度计算、迭代计算,搜索出一组(kp、ki、kd)使得全局解最优。将全局最优解对应的参数赋值给 Kp、Ki、Kd,画出单位阶跃曲线和适应度曲线。秃鹰算法整定PID参数系统框图如图1所示。

图1 秃鹰算法整定PID参数
根据被控对象模型,经过算法迭代寻找到全局最优解,然后将对应的最优参数代入PID控制器,在每个迭代周期开始时,首先需要确定秃鹰的搜索空间,再来更新秃鹰的位置、更新运动状态进行捕获行动,接着更新捕获行动中的位置,局部寻优的速度和准确性有所提高。
在算法优化参数的过程中,利用误差绝对值时间指标作为参数选择的最小目标函数,在目标函数中加入平方项,可以有效预防控制能量溢出,目标函数的公式如下:

同时为了避免超调,设置惩罚函数功能,即如果产生超调,将超调量作为最优指标其中的一项[6]。目标函数如下所示:

式中,ω1取值为 0.999,ω2取值为 0.01,(t)为误差,u(t)为控制器输出。
3 仿真实验与分析
3.1 实验仿真
实验基于Matlab平台,算法参数设置维度为3,种群数量为50,最大迭代次数为100,控制螺旋参数 a=10,R=1.5。在控制领域,典型的系统一般为一阶系统、二阶系统,为了验证秃鹰算法整定PID算法的性能,选用文献[7]中一个经典的控制系统模型进行测试,并且与PSO-PID进行比较,系统的开环传递函数如下:

基于该传递函数的适应度曲线如图2所示:

图2 最优适应度曲线
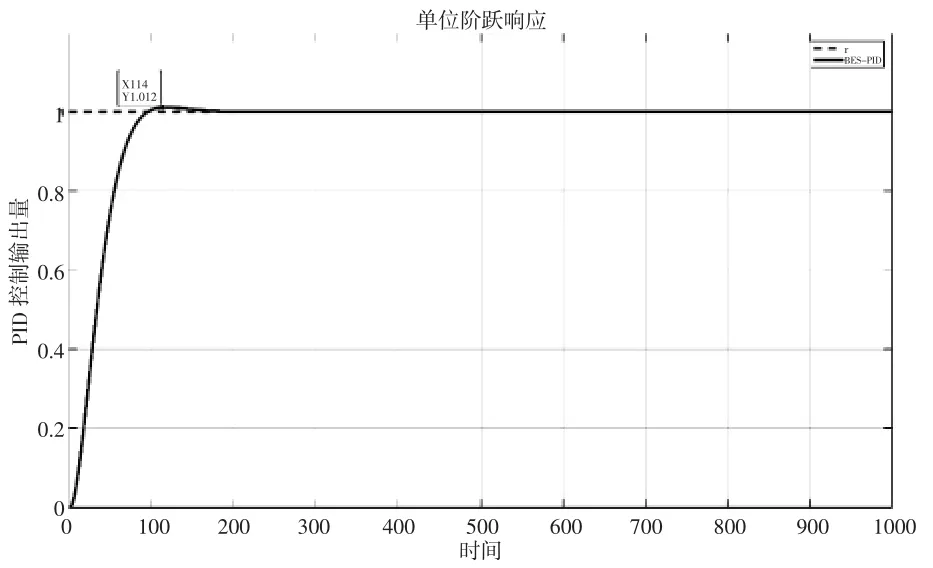
图3 BES-PID单位阶跃曲线

图4 PSO-PID单位阶跃曲线
3.2 实验结果分析
由实验的图像可以看出,基于秃鹰算法的PID参数整定下的适应度曲线相比PSO算法,通过较少的迭代之后达到稳定。单位阶跃曲线来看,BESPID的超调量峰值为1.012,小于PSO-PID的超调量峰值1.016。所以,BES算法的优化PID参数在最优适应度曲线的迭代次数和优化超调量方面皆优于PSO算法。
4 结论
本文引入了秃鹰算法进行PID参数整定,该算法具有较强的全局搜索能力,能有效解决比较复杂的寻优问题。输入信号为单位阶跃信号,以一种常见的开环控制模型为传递函数,并且与PSO粒子群算法进行了比较,通过对实验仿真结果的分析,得到了秃鹰算法在最优适应度曲线稳定所需时长以及超调量方面均优于PSO粒子群算法。
