大倾斜度弹簧刚度表达式的推导及有限元验证
2022-06-16钱宁伟李峥彬肖奉英沈逸舟黄模佳
钱宁伟,李峥彬,肖奉英,沈逸舟,黄模佳
(南昌大学工程力学系,江西 南昌 330031)
弹簧在机械系统中是一种较为常见的零件,且种类很多,其中圆柱弹簧在工程中的应用最为广泛[1-2]。圆柱弹簧一般受纵向荷载作用,利用自身的弹性和变形进行工作[3-4]。刚度作为弹簧性能的重要指标之一,对整体结构的安全性能起着重要作用,熊志远等[5]以弹簧材料为出发点对弹簧刚度进行分析,发现弹簧刚度与纤维弹性模量、簧丝外直径、纤维体积分数三者相关,刚度大小随三者增大而剧增,随三者的下降而骤减。金达锋等[6]基于层合板理论,利用纤维复合材料平板的剪切模量及各向同性材料弹簧刚度公式,理论推导了该类复合材料弹簧的刚度表达式。
目前圆柱弹簧的常用研究方法为采用有限元仿真计算。朱勋等[7]运用ABAQUS软件对圆柱弹簧进行分析,将有限元结果与已有的弹簧刚度公式[8-10]进行比较,结果表明文献[8]的公式更为通用。田树涛等[11]通过Solidworks软件对弹簧进行建模分析,基于不同加载方式获得弹簧刚度,研究表明该方式得到的弹簧刚度精度较高。周凯林等[12]利用ANSYS软件对弹簧进行建模,对弹簧刚度进行有限元仿真计算,并重点分析了弹簧簧丝间的接触问题。钟文彬[13]等通过ANSYS软件对弹簧各方向的刚度进行了仿真计算,研究表明有限元方法能为弹簧的精确设计和计算提供较为可靠的理论依据。
聂维等[14]通过编制 Matlab 程序对变参数圆柱弹簧的参数进行解析计算,给出基本的运算思路,结果表明变参数圆柱弹簧具有良好的非线性刚度特性。曹坤等[15-16]则是利用Matlab对圆柱螺旋弹簧进行优化设计,为工程中的弹簧设计提供一定的参考。
目前国内外对圆柱弹簧的研究虽然较多,且部分文献考虑螺旋角对弹簧刚度的影响,但计算分析的模型一般为密圈弹簧,对于螺旋角较大的弹簧没有进行分析,且关于密圈弹簧的计算结果的精度不高。基于上述情况,本文利用圆柱弹簧几何参数的关系,考虑螺旋角对弹簧刚度的影响,通过能量法给出精度较高的弹簧刚度理论解,并利用有限元软件进行仿真验证,基于解析解和有限元结果对工程中的弹簧设计提出一些建议和参考。
1 弹簧的倾斜度与弹簧尺寸的关系
圆柱弹簧是工程中较为常用的弹簧,目前工程中对于圆柱弹簧刚度K0的经典理论公式为:
(1)
式中:n为弹簧圈数;R为弹簧半径;G为弹簧材料的剪切模量;d为弹簧线径。式(1)表明弹簧刚度的大小主要由该4个几何参数决定,该式未考虑螺旋角对弹簧刚度的影响,实际上弹簧螺旋角对弹簧刚度的大小具有一定的影响。现假设圆柱弹簧的高为h,长度为L,螺旋角为α,将其进行展开,展开的模型参数如图1所示。
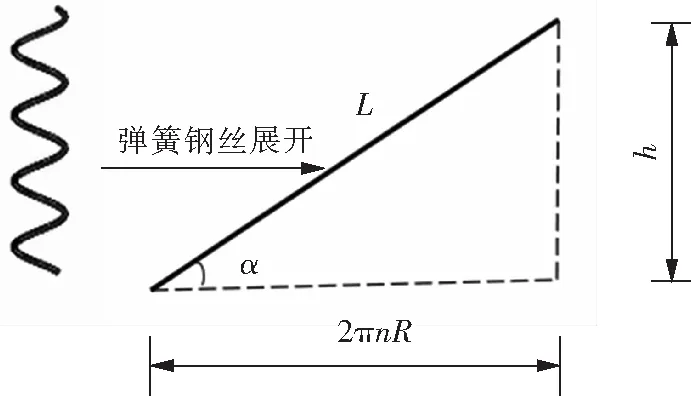
图1 圆柱弹簧模型
在圆柱弹簧变形过程中,提出与弹簧变形相符的两个基本假定:
(1) 弹簧的变形主要来自于钢丝的扭转和弯曲变形,在圆柱弹簧变形过程中钢丝弹簧局部轴向力很小,钢丝弹簧受力后钢丝的长度不变。
(2) 弹性变形过程中整个弹簧的形态不变,即圈数n不发生变化。这里n为弹簧变形前弹簧的圈数(注:n可以不是整数)。
为了将α与L和h之间关系较为简单地表示出来,引入参数κ表示弹簧变形前的α与L和h之间的关系,参数κ1表示受力弹簧变形后的α1与L1和h1之间的关系,κ可视为弹簧钢丝的倾斜度,根据两个基本假定值L1=L,n1=n,以及图1可得:
(2)
根据式(2)弹簧变形量Δh可表示为
Δh=L(κ1-κ)=Lχ,χ=(κ1-κ)
(3)
利用式(3)以及荷载P与弹簧变形量Δh之间为线性关系可得
P=K(κ)Δh=K(κ)Lχ
(4)
这里K(κ)是该弹簧刚度。
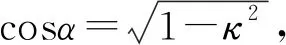
(5)
2 基于能量法推导弹簧刚度的解析表达式
将作用于弹簧中心的荷载P平移到弹簧钢丝上简化成主矩M0=PR、主矢P;其中主矩M0可分解成弹簧钢丝与弹簧垂直轴线的截面平行的弯矩M和与弹簧垂直轴线的截面垂直的扭矩T,主矢P可分解成弹簧钢丝与弹簧垂直轴线的截面平行的剪力Q和与弹簧垂直轴线的截面垂直的轴力N。力矩关系示意图见图2。
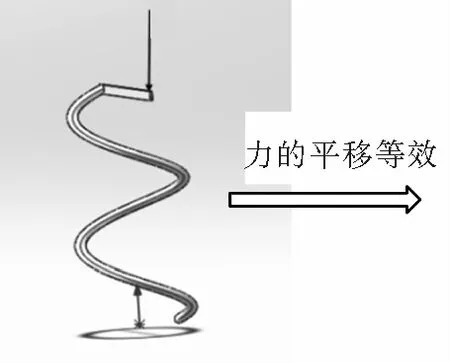
(a)
根据式(3)、式(4)可得弹簧刚度K(κ)为
(6)
荷载P对圆柱弹簧作用产生的力矩为M0,根据式
(4)和式(5)式可得
(7)
根据图2(c)所示的力、力矩分解的几何关系以及式(2)、式(4)、式(5),可得到扭矩T和弯矩M:
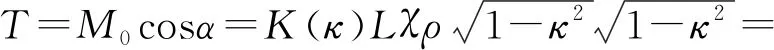
(8)
(9)
外力对弹簧做功对于小倾斜角弹簧而言主要转化为扭转变形能,仅考虑扭转变形能的弹簧刚度表达式为式(1),外力对弹簧做功对于大倾斜角弹簧而言弯曲变形能则是不可忽略的,对于大倾斜角弹簧主要考虑扭转变形能和弯曲变形能的共同作用。圆柱弹簧一端固定,另一端受到的外力荷载P作用在弹簧圈的正中心,外力做功WP转变成弹簧钢丝扭转变形能UT和弯曲变形能UM,即
WP=UT+UM
(10)
这里外力荷载P作用下弹簧钢丝截面上轴力N很小引起的变形能可以忽略不计,对于弹簧钢丝较细时外力荷载P作用下弹簧钢丝截面上剪力Q引起的变形能也可以忽略不计。
为了便于计算弹簧钢丝的扭转变形能UT和弯曲变形能UM,将弹簧钢丝看成为展开状态(如图1所示),根据材料力学公式以及式(8)、式(9)可知在扭矩T和弯矩M的作用下产生的扭转变形能UT和弯曲变形能UM为
(11)
(12)
这里Ip为弹簧钢丝横截面的极惯性矩,E为弹簧钢丝的弹性模量,Iz为弹簧钢丝横截面的惯性矩。
根据式(3)、式(4),可得外力P对弹簧做的总功WP为
(13)
弹性模量E和剪切模量G满足
E=2G(1+ν),其中ν为弹簧材料的泊松比,将式(11)~式(13)代入式(10)得到
(14)
根据式(14)等式左右两边约去χ2,即可求得K(κ)
(15)
根据式(1)、式(15)整理后得到的弹簧刚度解析解为
(16)
式(16)表明弹簧刚度与弹簧的螺旋升角、泊松比相关,式(16)中的η为刚度影响系数。式(1)主要考虑扭矩T作用推导出的弹簧刚度表达式K0,而式(16)考虑扭矩T和弯矩M共同作用推导出精确的弹簧刚度表达式K(κ),比较式(1)和式(16)可知K0η为考虑弯矩作用下对弹簧刚度的影响量。当κ=0时,η=0,即K(κ)=K0,这时弹簧仅受扭矩T的作用;当κ≠0时,影响刚度系数η则会随初始螺旋升角的大小发生变化,为了更加直观地看到螺旋升角对弹簧刚度的影响,考虑泊松比ν=0.2,0.3,0.4时η随着倾斜度κ的变化,结果如表1所示。
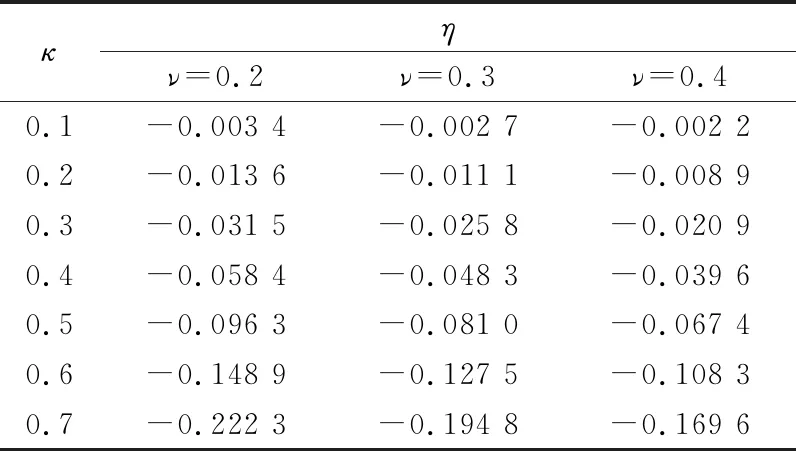
表1 影响刚度系数
可知,当倾斜度κ较小时,η对弹簧刚度影响值较小,此时按式(1)或式(16)计算弹簧刚度均可;当倾斜度κ较大时,η对弹簧刚度影响值很大,此时计算弹簧刚度应按照式(16)中的K(κ)=K0(1+η)计算;对于给定倾斜度κ泊松比ν越小,η对弹簧刚度影响值越大;泊松比ν越大,η对弹簧刚度影响值越小,因此对于泊松比ν较小且倾斜度κ较大的情况,更宜用式(16)来计算弹簧的刚度以保证弹簧刚度的准确性。
3 含倾斜度的弹簧刚度的有限元仿真验证
为了验证能量法求解得到的弹簧刚度表达式的准确性,利用ABAQUS有限元软件对弹簧进行有限元仿真验证。式(16)主要应用于计算螺旋升角较大的弹簧的刚度,故有限元计算模型选用螺旋升角不同的模型进行对比分析,为了更好地展示螺旋升角对弹簧刚度的影响,所有弹簧有限元模型中的弹簧圈的半径R、弹簧钢丝的弹性模量E、泊松比ν、弹簧钢丝的直径d、弹簧的圈数n均相同,仅改变弹簧的倾斜度κ的值。
3.1 弹簧有限元模型的建立与网格划分
弹簧有限元计算选用三维梁元进行分析计算,首先通过ABAQUS软件建模功能输入相应的参数形成弹簧,给定弹簧圈的半径R=0.015 m,弹簧的圈数n=5,以及弹簧钢丝的直径d=0.002 m,并给弹簧赋予材料属性,材料的弹性模量E=206 GPa,泊松比ν=0.3,将已经赋予材料属性的弹簧进行装配,装配完成后,在分析步功能栏增加荷载分析步,选用线性分析计算。
为了证明式(16)不仅适用于螺旋升角较小的圆柱弹簧,对于螺旋角较大的弹簧也同样适用,且精度较高,本文将选用一组弹簧模型进行有限元仿真计算,该组弹簧模型取κ为变量,弹簧的高度h、弹簧钢丝的长度L随变量κ的变化规律如表2所示。
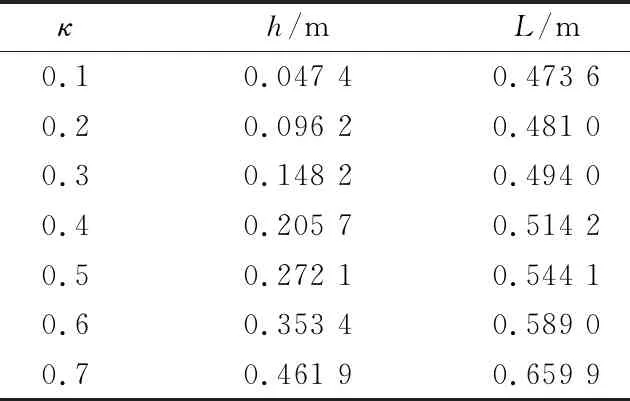
表2 弹簧尺寸的选取
当弹簧模型建立完成后,对其进行加载以及设置约束。在弹簧的顶部施加荷载P,荷载P位于弹簧的正中心,荷载P的大小为0.02 kN,荷载方向朝Z的负方向。在弹簧的底部设置完全固定约束,最后对弹簧模型进行网格划分,网格划分选用B31(两节点空间线性梁单元)单元。
3.2 有限元结果与解析解的比较情况
对弹簧有限元模型进行仿真计算,提取弹簧κ=0.1、弹簧κ=0.2的位移云图进行分析,如图3所示。
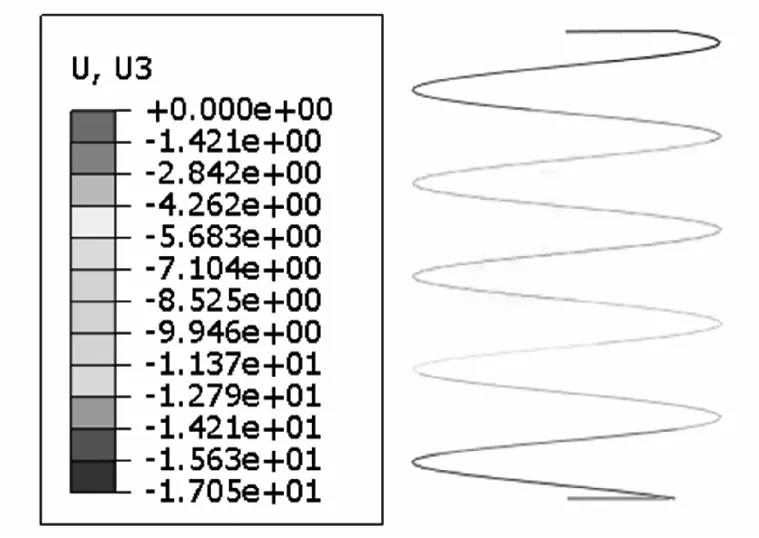
(a) κ=0.1位移云图
可得,弹簧其他参数相同、荷载相同、初始螺旋升角大小不同的情况下,弹簧产生的位移不同,即刚度大小不一样,可见初始螺旋升角对弹簧刚度的大小会产生一定的影响。现提取7种模型的有限元计算结果,由设置的弹簧模型参数可知,7种弹簧模型中,根据弹簧的倾斜度κ的变化,以及弹簧受力后的变形量Δh,计算出有限元仿真的弹簧刚度结果K1=P/Δh,根据式(16)可得不含倾斜度效应的弹簧刚度K0=1 173.789 N·m-1,以及荷载作用下考虑扭转和弯矩共同作用的弹簧刚度表达式K(κ)=K0(1+η),不含倾斜度效应的弹簧刚度与有限元仿真计算的弹簧刚度误差ξ1=(K1-K0)/K1,考虑倾斜度效应的弹簧刚度理论解与有限元仿真计算的弹簧刚度误差ξ2=(K1-K0(1+η))/K1,结果如表3所示。
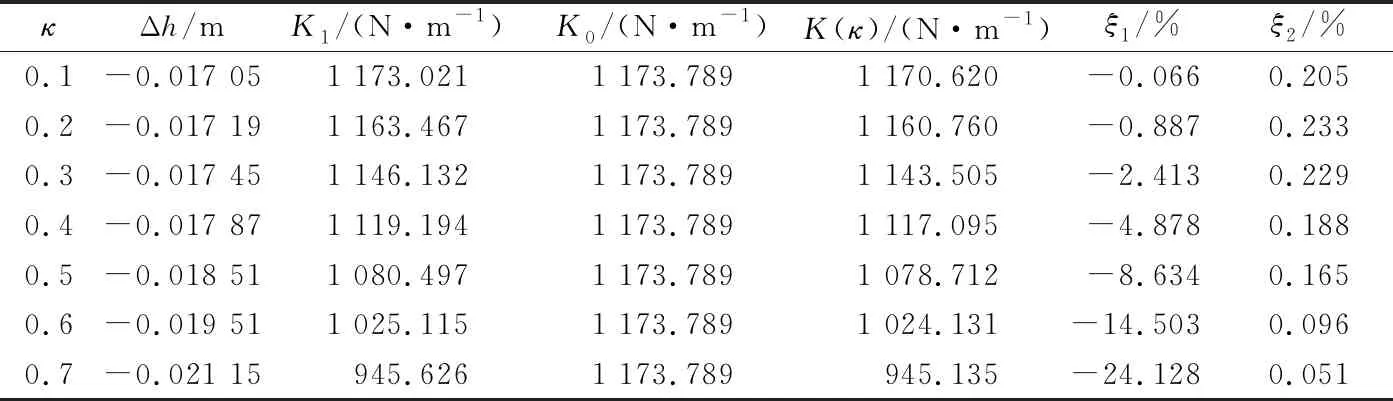
表3 弹簧刚度的变化及相对误差
由表3的有限元结果可得,倾斜度κ的值越大,弹簧刚度越小;从整体分析可得,当倾斜度κ的值较小时,式(1)、式(16)的值与有限元值均比较吻合,此时式(1)、式(16)中的表达式均可用于工程中的弹簧设计;当初始倾斜度κ的值较大时,式(1)与有限元值的差值越来越大,当κ≥0.2时,式(16)的精确度高于式(1)的精确度,且式(16)随着κ值增加误差变小而式(1)随着κ值增加误差变大,此时必须考虑弹簧倾钢丝斜度的影响,并且应当选取式(16)计算弹簧刚度。
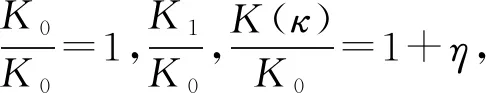
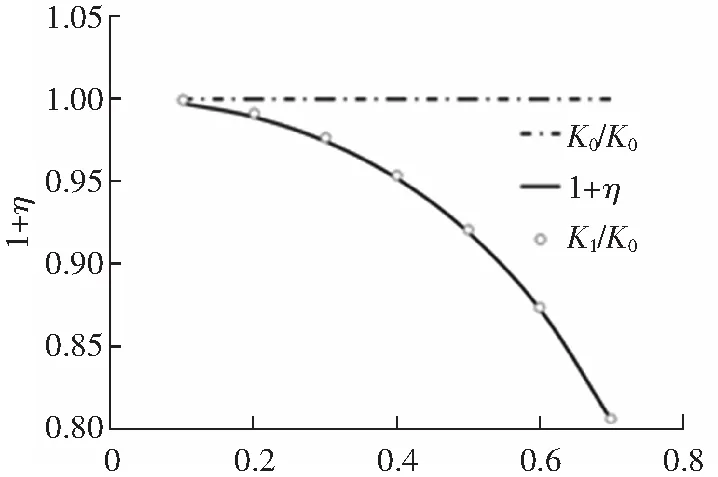
κ
可知,有限元无量纲化的结果与本文中考虑倾斜度弹簧刚度表达式式(16)无量纲化后的结果曲线十分吻合,曲率变化也接近。当弹簧倾斜度κ逐渐增大,有限元结果K1与K(κ)结果越来越接近,两者之间差值幅度也越来越小,而有限元结果K1与不含有倾斜度的弹簧刚度表达式K0差值的幅度越来越大,由此可见,式(16)的适用性更高。
4 结论
本文利用弹簧自身的参数及变化特性,考虑倾斜度即螺旋角对弹簧刚度的影响,基于能量法对其刚度进行求解,并借助有限元仿真软件进行验证,将所得结果与经典理论公式和本文推导得到的解析解进行比较,结论如下:
(1)由有限元结果可证明螺旋角对弹簧刚度的大小会产生影响,且同等条件下,倾斜度较大的,刚度值反而更小。
(2)由能量法推导得到的解析解与有限元计算结果基本吻合,不仅验证了解析解的正确性,同时由差值结果可证明该解析解的精度较高。
(3)经典理论公式仅适用于倾斜度较小的弹簧,本文的公式不仅适用于密圈弹簧,对于倾斜度较大的圆柱弹簧同样适用,且误差均小于0.21%,可为工程中的弹簧刚度设计提供较为可靠的理论解。
