碳优化

碳减排过程涉及很多需要优化的问题，数学在这一方面大有可为，但在实际中，问题要复杂得多，优化要应用更复杂的数学工具，如数学规划、泛函分析和最优控制中的哈密顿—雅可比—贝尔曼方程（HJB方程）。碳优化几乎在双碳行动的所有领域都很活跃。

碳减排肯定是要花钱的，而且花了钱也没有立竿见影。这也从某种程度抑制了人们的减排动力。政府就要有所作为，一方面发放一定的排放许可，一方面对排放超标的企业进行处罚。所以对于国家或者一个企业，这里就有一个减排的最优控制问题，如何花最少的钱达到减排达标的效果。数学最拿手的就是处理这类最优控制问题。数学中有很多方法，要做的事就是建立数学模型，搞清楚优化目标和控制变量，然后应用数学方法控制变量，求到最优的效果，以达到目的。

假设一个国家通过签订国际公约的方式，或者一个企业接受减排要求约定在给定期限内降低其碳排放量到一定限额以内，否则到期需要为超过限额的碳排放量支付罚款。那么在此期间，他们就需要采取一定措施降低国内或企业的碳排放量。考虑到碳减排的成本，该国或企业需要选取适当的碳减排策略，使得减排过程中的总费用和到期由于超额碳排放产生的罚款总和最小。能采取的措施有很多选择，数学可以帮助决策者做出最优的决策。

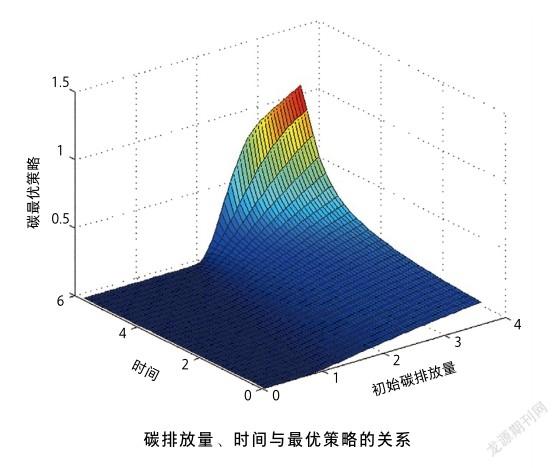
对政府和企业来说，最优投资的含义就更复杂些，但可以认为是在有限资金下最优分配资金进行碳投资。如政府有一笔定量投资减碳，是投在绿色能源？植树造林？减排技术革新？还是培养教育低碳人才？亦或分配这笔资金使之取得的减排效果最好。即便是投在绿色能源，那么是风能还是水能，在什么地方，用什么技术和设备才能使投资最小而效果最好都是优化问题。

在这些优化控制中，数学的优化方法大有可为。主要有：线性规划、微积分最值、泛函分析、微分方程等。

具体到一个企业，生产是企业活动的基础。但要生产就有碳排，碳排有限制，为减排就要投资，这又会影响企业利润，如何平衡？下面通过一个例子来说明如何应用数学来解决这个问题。

例1 一个企业生产某产品，收益与生产量成正比，比例系数为α。同时，生产过程产生碳排放，排放的多少与生产量成正比，比例系数β。如果碳排放超过许可Q，企业将面临高额罚款。为了解决碳排放问题，企业有两个选择：或者缩小生产规模以控制碳排放在许可范围内，或者投资减排。投资费用与减排量的平方成正比，其比例系数为γ。制定最优的减排方案使得碳排放在许可范围内，并且收益最大，开销最小。

我们来分析一下这个问题。出于企业盈利考虑，当然生产越多越好，但生产多，带来的碳排放就越大。碳排放的许可限制了企业的生产量。但如果企业花些钱投资减排，可以扩大生产量，但投资将增加成本，那么投资多少才可达到最优？

下图可以更直观地表述问题。参数取为α=β=γ=1，Q=c=0。图中实线即企业收益P，虚线即企业减排成本B。则对于给定生产量x（横坐标），实线超过虚线的部分即企业净收益。则最优解即使得两条线“距离最远”的点。

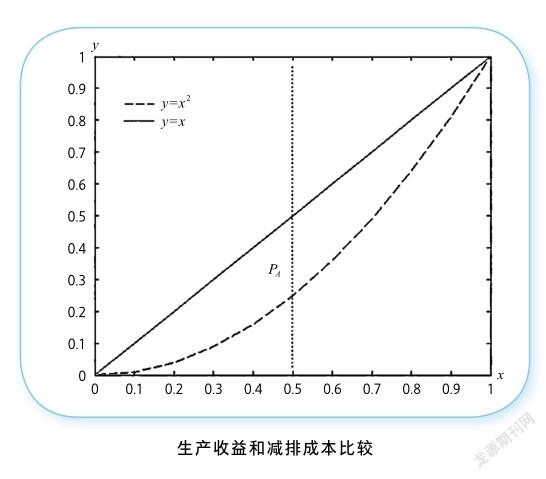
得到的最优解有若干参数。根据结果和参数分析，可以得到如下结果：

首先最优生产量x*比Q/β来得大，这意味着，碳排投资是必要的，扣除碳排费用，在碳排上限的限制下，企业可以获得更大的收益。

最优生产量x*随β增大而减小，这意味着企业增进生产技术，减少生产中碳排率可以有进一步扩大生产的空间，使得企业获益更大。

最优生产量x*随γ增大而减小，这提示企业增进碳排技术，减少减排消耗率可以有进一步扩大生产的空间，使得企业获益更大。

最优生产量x*随α增大而增加，这表明生产收益率始终是重要的。

如果考虑更多的因素，如碳排放量是随机的，企业可以购买碳排权，而市场价也是随机的等等，那么数学模型会更复杂。

对政府或其他投资者来说，除了低碳行动，还可以对一些碳项目进行投资。如果可以投资的一些项目风险和收益都清楚的话，投资者可以选择在风险一定的情况下，使组合投资项目达到收益最高的结果，或者在收益水平一定的情况下，调整投资组合使得自己的投资风险最低。也可以结合这两个优化目标或加上其他投资目标构造投资组合以达目标。同样来看个例子。

例2 某市要评估5个碳减排项目，初始投资资金是有限的5000万，以后每年的维护资金是800万。项目只有选择完全投资或者完全不投资，收益预期和产生的减碳排效益及初始资金即维护资金如下表所示。考虑如何安排投资项目使得在可运行资金范围内使得产生的碳排放效果最好。

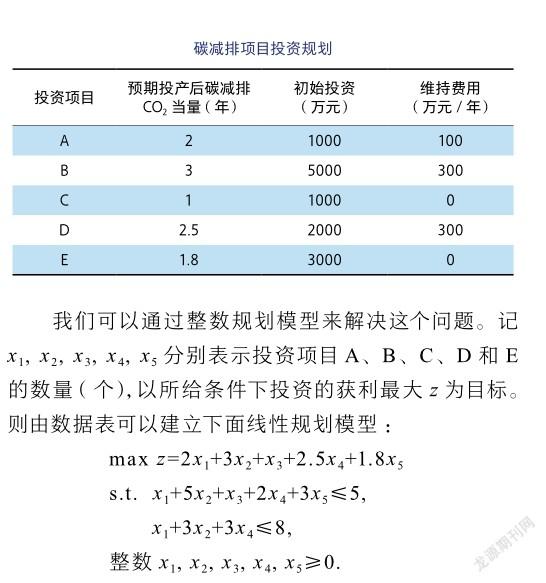
然后通过直接计算或计算机计算，可以算出最佳的方案是所有的資金都投A项目，即投5个A项目，每年可碳减10个单位。但如果有限制条件，每个项目最多投一个，则问题可归为0-1规划，计算结果为投A、C、D项目，每年可碳减5.5个单位。

碳减排不是说减就可以减的。一家企业要减排，就要引进和它生产方式有关的技术，购买相应的设备。一般来说，减排越早越好，但也不尽然。减排技术在不断发展，引进技术的费用可能越来越低，在引进的时间，企业要付出沉没成本，即一旦钱花出去了就不能收回，同时也失去了等待的机会。所以，如何选择最优的引进技术时间，是一个数学的优化问题。金融数学中处理实物期权的方法可以借鉴。

例如，一家企业拟引进一项技术，引进前后描述碳排放的随机过程发生了变化。可以假定碳排率下降了，但是引进时企业要付出沉没成本，引进后还要支出管理费用。沉没成本也是一个随机过程，可能随着时间而变化。那么从今天来看，从最经济的角度，什么时候引入这项技术有可能是最好的。这个问题可以建一个数学模型，并转化成数学中所谓的HJB方程或者自由边界问题来讨论。

双碳运动，人人有责。对于个人来说，不是喊喊口号就是支持双碳，要身体力行实施减碳。然而，现代生活讲究效率，减碳并不是要降低生活质量，而是要在这之间找到平衡，安排自己在能完成工作和正常生活的前提下选择最减排的方案。这也是普通人可以做到的。再看一个例子。

例3 某人公干，希望低碳出行。下表显示使用各种交通工具的碳排放数据，以及出行速度和旅费。如果目的地与出发地相距400千米，要求两天来回，路上时间每天只能花2小时，飞机可飞行350千米，火车可行驶380千米，飞机和火车中途不可以下车，也不可以同时乘，单程旅费限制200元。如何选择交通工具，使得完成任务的同时碳排放最少？

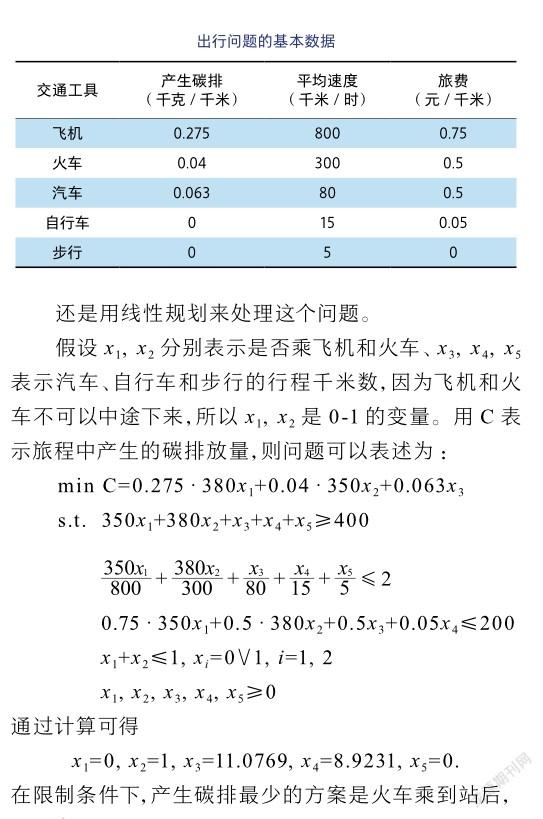
数学在碳优化方面的应用远不止这几个方面，方法也不止所提及的几种，但我们已可以从中理解数学在碳优化方面的强大优势。

上述事例只是数学应用的几个方面，总之，随着双碳运动的进行，数学将越来越显示出她的强大力量，并在双碳这个领域长袖善舞，发挥着至关重要又不可取代的作用。

2020年筆者总结了近十年关于碳减排方面的数学研究工作，包括笔者两位博士生的博士论文的内容，出版了一本科普书《碳减排数学模型与应用》，其中详细而具体地阐述了本文提到的碳减排方方面面的数学应用。

最后，希望数学可以为减排、为优化控制、为科学管理、为地球减负……为人类做出更大的贡献。也更热切地希望碳减排的议题受到各行各业、从政府到百姓更加强烈的重视，身体力行，同心合力减排。

因为地球只有一个，我们只能同舟共济！

[1]梁进，杨晓丽，郭华英. 碳减排数学模型与应用. 北京：化学工业出版社，2020.

关键词：碳优化 碳减排 数学模型 ■