考虑改造升级风险的复杂产品模块智能聚类方法

张 芹,潘金龙,洪兆溪

(1.湖州职业技术学院机电与汽车工程学院，浙江 湖州 313000)

(2.上海航天动力技术研究所，上海 201109)

(3.浙江大学流体动力与机电系统国家重点实验室，浙江 杭州 310027)

为提高生产效率、降低设备维护成本以及响应国家号召，节能降耗，常常要对在役产品进行改造升级，以提升企业竞争力。由于复杂机电产品零部件间存在较强的耦合关系，在产品改造升级过程中面临的问题有：部分零部件改造升级会对其他零部件结构、功能产生影响，增加升级风险，待升级零部件拆卸困难，甚至需要破坏其他零部件结构才能进行拆卸，增加升级难度，因此在设计初期若能考虑影响产品改造升级的因素，对促进产品快速响应外部需求具有重要意义。模块化设计技术在产品设计研发过程中的应用逐渐得到普及，合理的模块化设计可以实现功能模块的重用和互换，对提升产品改造升级性能具有重要影响。

对相关性强的零部件进行聚类即可实现产品的模块划分。模块划分是实现模块化设计制造的基础[1]，也是近年来国内外学者研究的热点。李婷婷等[2]在综合考虑产品零部件间的功能、维修等相关属性的基础上，利用动态模糊聚类实现了产品的模块划分；Yan等[3]从可持续发展角度的出发，通过对零部件聚类实现了产品模块划分；Sakundarini等[4]分析了零部件间的功能、结构、寿命、材料以及回收等相关属性，面向产品生命周期实现了模块划分；Stone等[5]综合分析了产品零部件间能量流、物料流、信号流，对产品进行模块划分；潘双夏等[6]综合考虑客户需求、产品装配、成本等因素，运用模糊聚类实现了产品的模块划分；康博凯等[7]针对报废产品资源回收和利用问题，以提高产品再制造升级性能为目标，对产品进行模块划分；王奇瑞等[8]通过量化零部件间直接和间接连接关系，实现模块精确划分；翁力炜等[9]分析了产品的功能、行为及制造可行性，在此基础上应用模糊聚类实现模块划分；吕健等[10]为提升产品的生产、装配以及后期维护效率，利用凝聚层次聚类算法对零部件进行聚类，获得模块划分方案。以上关于模块划分的研究主要从产品维修、装配、再制造、回收等角度出发，缺乏对产品服役阶段改造升级风险的考虑，导致产生的模块化结构不能有效支持产品改造升级，从而增加了产品升级的难度和成本。

针对上述问题，本文提出了考虑改造升级风险的复杂产品模块智能聚类方法。综合考虑影响产品改造升级风险的因素，从功能、结构、关联更改概率、拆卸等4个方面定义零部件相关属性，构建零部件间综合关联矩阵，采用改进人工蜂群(im-proved artificial bee colony，IABC)算法和密度峰值聚类( density peaks clustering，DPC) 算法相结合的智能聚类方法求解，以模块划分质量为优化目标，优选截断距离，获得最优模块划分方案，以降低产品改造升级的难度。

1 产品改造升级相关性分析

1.1 功能相关性

为满足生产需求，通常需要为在役产品增加新功能或进行功能升级。由于产品的某一种功能通常由多个零部件组合关联实现，即零部件间具有功能相关性，因此为便于在产品改造过程中增加或者升级功能，且不对其他功能产生影响，需要将功能相关性强的零部件聚类至相同模块，以保证产品各功能的相互独立性。定义零部件i和零部件j间的功能关联度为Rij，其功能关联描述与对应的关联度值见表1。

表1 零部件功能相关性评价标准

1.2 结构相关性

产品功能的实现与其结构密切相关。产品零部件间不仅具有一定的连接关系，其结构特征间也存在一定的约束关系。由于一个零部件通常具有多种结构特征，且结构特征间存在一定的约束关系，产品改造升级过程中对部分零部件结构特征进行改造时，为保证其他相关零部件与改造后的零部件进行正确安装、连接、配合等，需要对与其具有密切关系的零部件进行改造，因此需要将结构特征密切相关的零部件聚类至相同模块，减少模块间的耦合度，尽可能对同一模块内零部件结构进行改造，减少该模块对其他模块零部件结构和功能的影响，降低产品改造升级的风险和难度。零部件i和j间的结构关联度值Gij见表2。

表2 零部件结构相关评价标准

1.3 关联更改概率

复杂产品零部件间具有复杂的关联关系，当一个零件发生改变时，其他相关零部件也会受到不同程度的影响从而发生连锁变更，本文将其定义为零部件关联更改概率。为提升产品改造升级能力，减少连锁变更强度，需要将关联更改概率大的零部件聚类在同一模块，以减少模块间关联变更风险。

图1所示为传统零部件关联网络模型，有向箭头表示一个零件的改变对另一个零件具有影响，虽然广泛应用于表征零部件间的关系，但是没有表达零部件间的某些逻辑关系。而零部件间存在多种逻辑关系，产品改造升级可能导致零部件尺寸特征间的关联更改，因此有必要描述零部件间的逻辑关系。

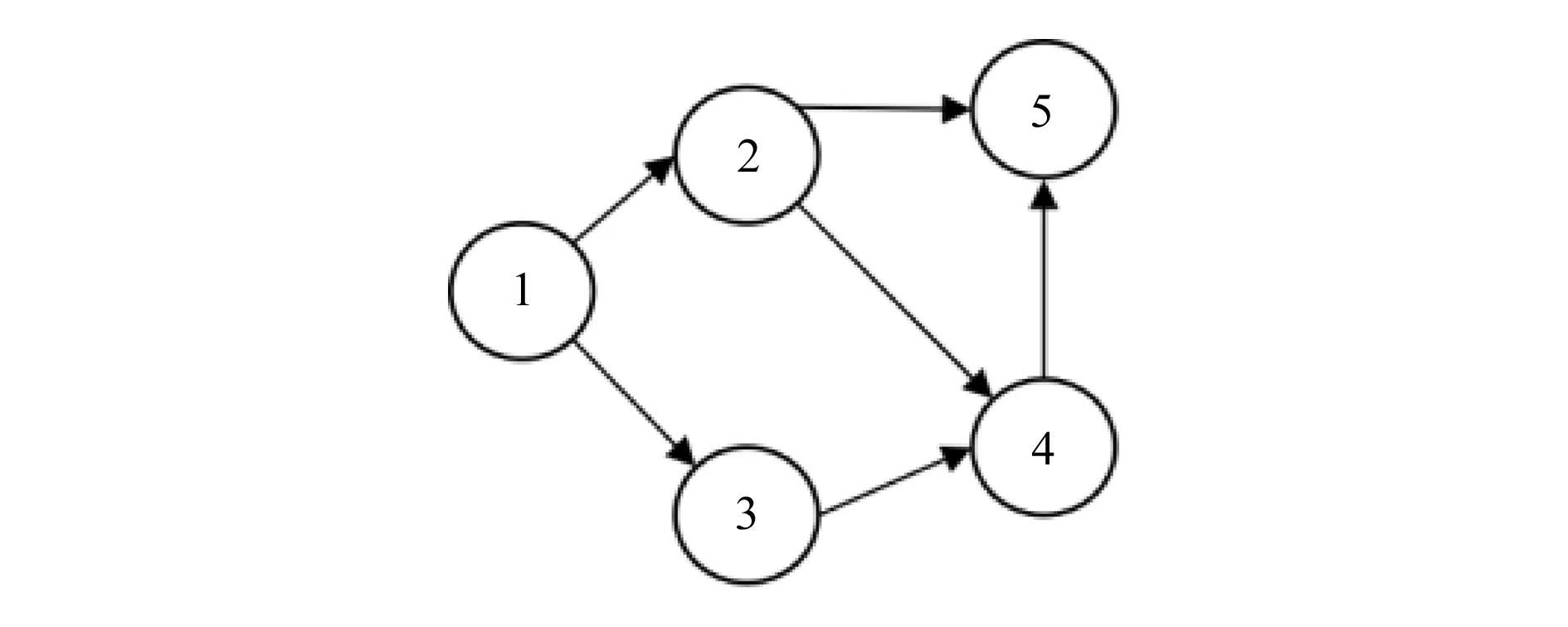
图1 传统网络图模型

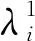
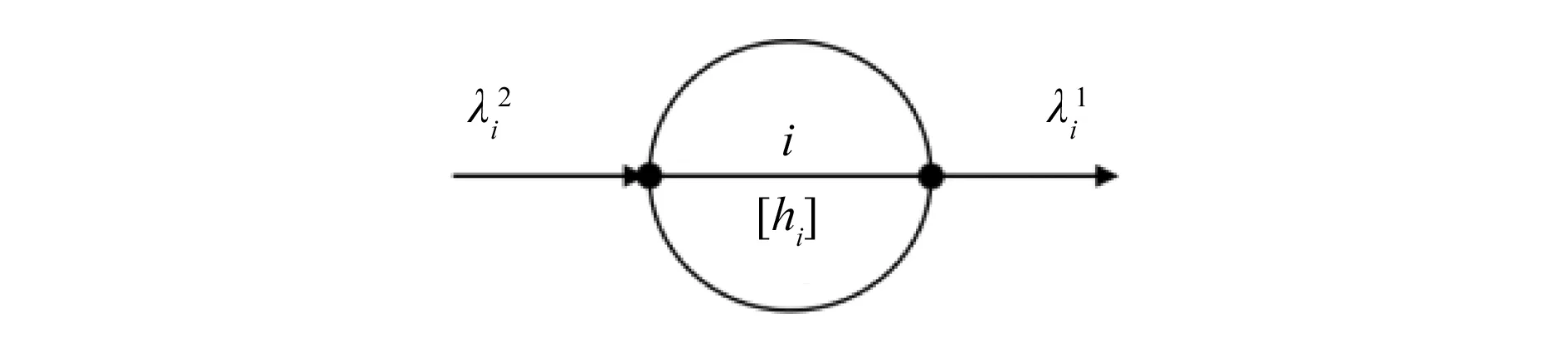
图2 特征逻辑元模型

(1)

1.4 拆卸相关性

拆卸是产品改造升级的基础，将关联性强的零部件聚类至同一模块，可以有效减少模块间的接口数量和降低模块间的拆卸复杂度，并且可减少拆卸引起的零部件损坏。零部件间拆卸相关性强弱由连接接口类型以及数量决定，定义零部件i和零部件j之间的拆卸相关性Fij为零部件间的连接接口交互系数之和，如式(2)，P(i,j)为零部件i和零部件j间连接接口的数量，Xh为零部件i和零部件j间第h个连接接口的交互系数。零部件连接交互系数的计算参考文献[11]。

(2)

1.5 零部件间综合关联矩阵

综合考虑影响产品改造升级的因素，参考文献[12]，利用层次分析法(AHP)计算零部件间相关性指标的权重系数ω1，ω2,ω3,ω4，通过加权求和获得零部件i和零部件j间综合关联系数Sij，构建零部件间综合关联矩阵S。

(3)

(4)

式中：n为零部件个数。

2 基于DPC算法的零部件聚类

通过将密切关联的零部件聚类至相同模块即可实现模块划分，因此零部件间综合关联系数Sij对模块划分具有重要影响，Sij越大表明零部件间相关性越强，Sij越小表明零部件间相关性越弱。依据密度峰值聚类算法原理，用零部件i和零部件j间的距离d(i,j)表示零部件间的关联强度，定义距离公式为：

d(i,j)=1-Sij

(5)

距离d(i,j)越小，表明零部件i和零部件j间的相关性越大。对于离散数据而言，零部件i的局部密度ρi为：

(6)

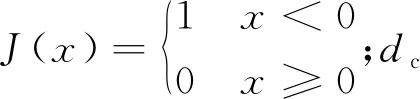
dc=d(j)×2%

(7)

式中：d(j)为任意零部件间距离的升序排列。将零部件i的局部密度ρi按照从大到小的顺序排列，满足ρindex1≥ρindex2≥…≥ρindexn，其中ρindexi为零件indexi的局部密度。定义相对距离γ(indexi)为零件与最近高密度零件间的距离d(indexi,j)，如式(8)所示：

(8)

聚类中心衡量指数Ii为：

(9)

利用以上方法自动获得聚类中心，并依据公式确定截断距离，即可完成零部件的聚类。

3 结合改进人工蜂群算法的密度峰值聚类

3.1 改进人工蜂群算法

人工蜂群算法主要包括引领、跟随和侦察3个阶段[14]，实现过程如下。

引领阶段：引领蜂根据式(10)搜索附近的食物源，生成候选方案，通过比较候选方案的适应度值大小，保留适应度值最高的食物源[15]。

Vij=Xkj+φij(Xij-Xkj)

(10)

式中：Vij为在蜂蜜源Xij附近生成的新蜂蜜源的位置；φij为随机数，且φij∈(-1,1)；k=1,2,…,n且k≠i。完成搜索后，引领蜂采用摇摆舞形式给跟随蜂传递蜂蜜源信息[16-17]。

跟随阶段：跟随蜂根据式(11)计算跟随引领蜂的概率Pi：

(11)

式中：fiti为对应蜜源的适应度值。fiti计算公式为：

(12)

式中：f(Xi)为目标函数值。

侦察阶段：如果在有限的周期后蜂蜜源Xi没有得到明显改善，则放弃蜂蜜源Xi。根据式(10)更新蜂蜜源，依附在蜂蜜源Xi的引领蜂转变为侦察蜂。

经过分析可知，在跟随阶段，跟随蜂通过比较适应度值选择并更新蜂蜜源位置。由于受参数φij约束，跟随蜂只能缓慢逼近局部最优解，而不能快速精细搜索，影响了算法收敛速度和精度，因此参考文献[18]、[19]，在跟随阶段引入动态混沌权重因子作为收敛因子，表示如下：

ω(t+1)=4ω(t)·(1-ω(t))

(13)

式中：ω(t)为随机数，且ω(t)∈(0,1)，t为当前迭代次数。跟随阶段蜂蜜源位置按照式(14)更新：

Vij=ω(t)·λ·Xij+φij(Xij-Xkj)

λ=(tmax-t)/tmax

(14)

式中：tmax为最大迭代次数。

3.2 DPC算法截断距离优选策略

利用密度峰值聚类算法对零部件聚类可获得产品模块划分方案，截断距离不同，模块划分方案也不同。由于截断距离dc受人为因素影响较大，敏感度高，因此本文利用改进人工蜂群算法对截断距离dc进行优选，以获取最优模块划分方案。将关联度大的零部件聚类至相同模块，实现产品的模块划分。模块内零部件间关联度越大，模块间零部件关联度越小，则模块划分质量就越高[20]。基于此，本文利用模块间耦合度和模块内零部件聚合度的比值JU来衡量模块划分的质量。模块内零部件聚合关系以及模块间的耦合关系如图3所示。

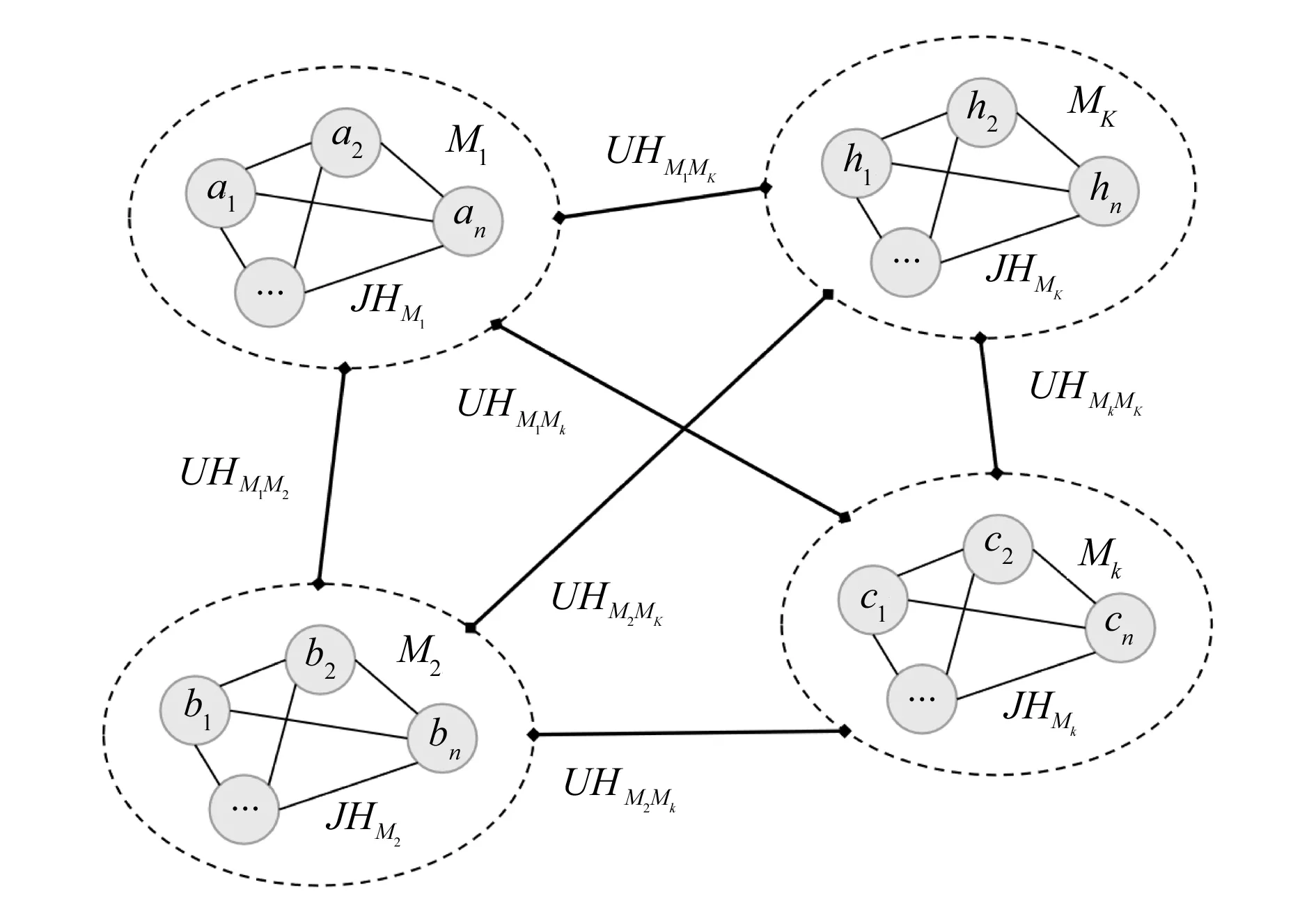
图3 模块内聚合度与模块间耦合度示意图

图中JHMk为模块Mk的聚合度，UHMkMK为模块Mk和MK间耦合度，K为模块总数。

模块内聚合度JH和模块间耦合度UH的计算式为：

(15)

(16)

式中：max(Sij)为对应的零部件综合关联系数最大值；Mik为零部件i与模块Mk的隶属关系，Mik=1时，表示零部件i属于模块Mk，Mik=0时，表示零部件i不属于模块Mk。Miλ和Mjη的含义与Mik同理。

JU的计算式如下：

(17)

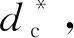
3.3 基于IABC-DPC零件聚类流程

本文提出的IABC-DPC算法首先根据式(8)、(9)确定零件聚类中心，然后将改进人工蜂群算法和密度峰值聚类算法相结合，以模块划分质量为优化目标，对截断距离dc实现优选。图4所示为IABC-DPC算法流程。

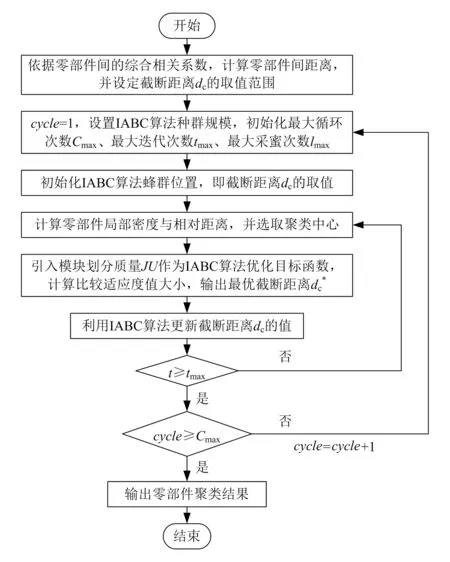
图4 IABC-DPC算法流程

4 案例验证

本文以某升降电梯的模块划分为例，分别采用DPC算法和IABC-DPC算法对电梯零部件进行聚类，对比模块划分结果，验证本文提出的模块聚类算法的有效性和可行性。图5为电梯零部件三维模型示意图，表3为电梯主要零部件清单。通过对电梯零部件进行改造升级的相关性分析，确定各零部件间的关联系数，参考文献[12]计算零部件间相关性指标权重，分别为ω1=0.353，ω2=0.241，ω3=0.225，ω4=0.181，分析计算零部件间功能关联度、结构关联度、关联更改概率、拆卸关联度，依据式(3)加权求和获得零部件i和零部件j间综合关联系数Sij，构建零部件间综合关联矩阵，见表4。利用本文提出的IABC-DPC聚类算法求解最优电梯模块划分方案，算法参数设置见表5。最终将零部件聚类为5个模块，分别为K1{1，2，3，4，5，6，7，16，21，22，23，24，43，44，45}、K2{8，9，10，11，12，13，14，15}、K3{17，18，19，20，36，37，38，39}、K4{25，26，27，28，29,30,31，32，33，34，35}、K5{40，41，42，47，48，49，46}，模块间耦合度和模块内零部件聚合度的比值JU为0.039 1。

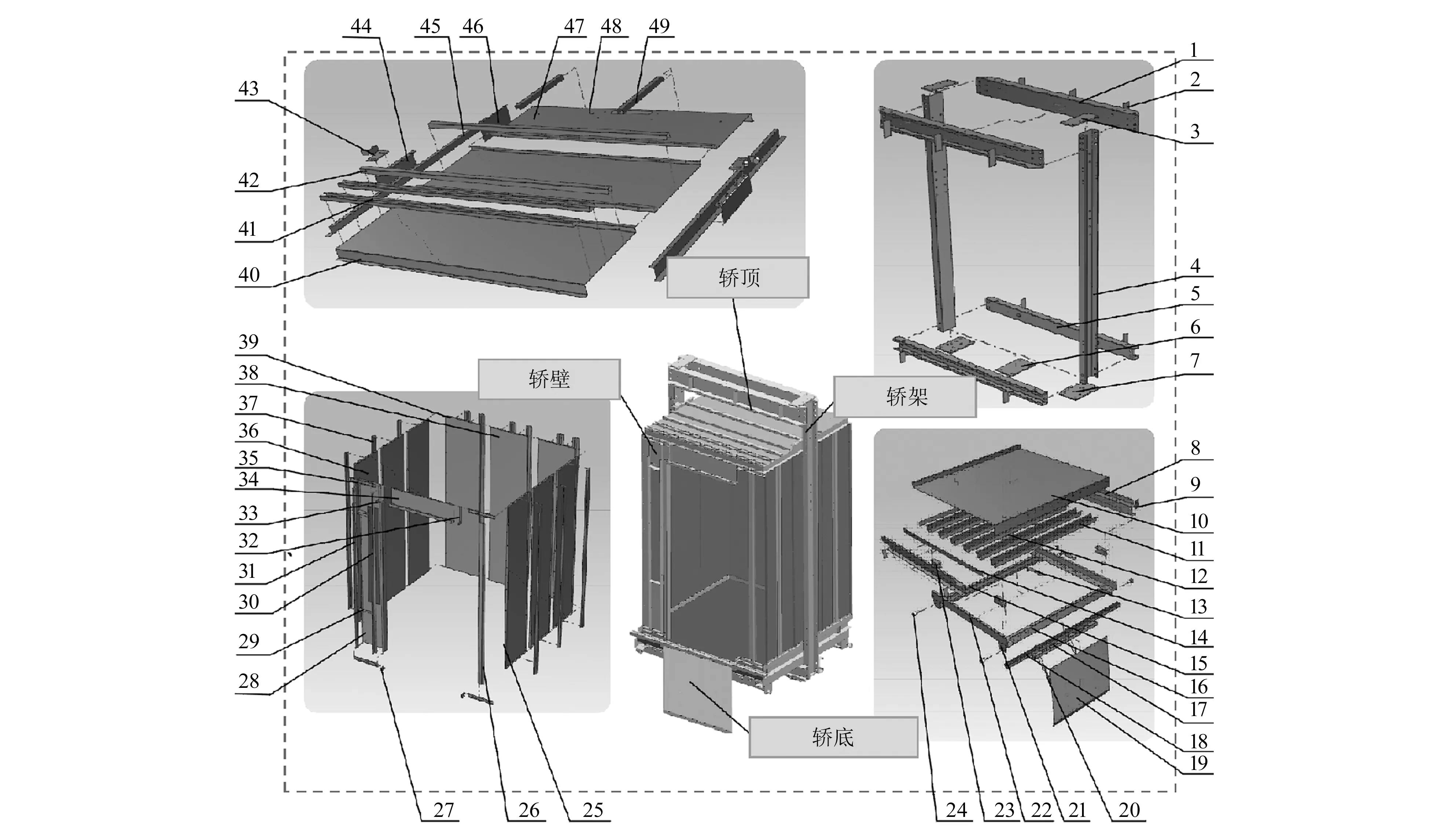
图5 电梯零部件三维模型

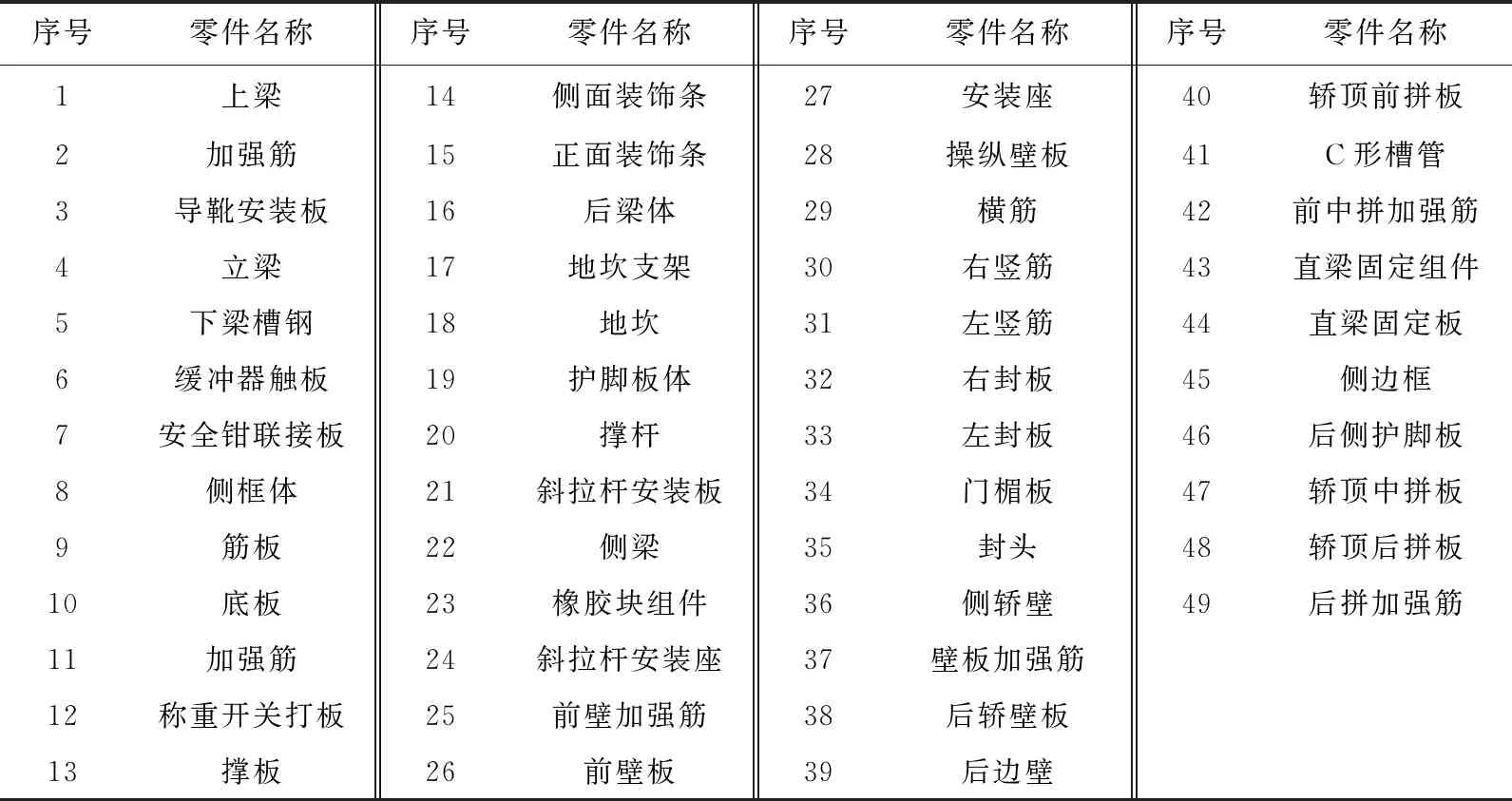
表3 零部件列表

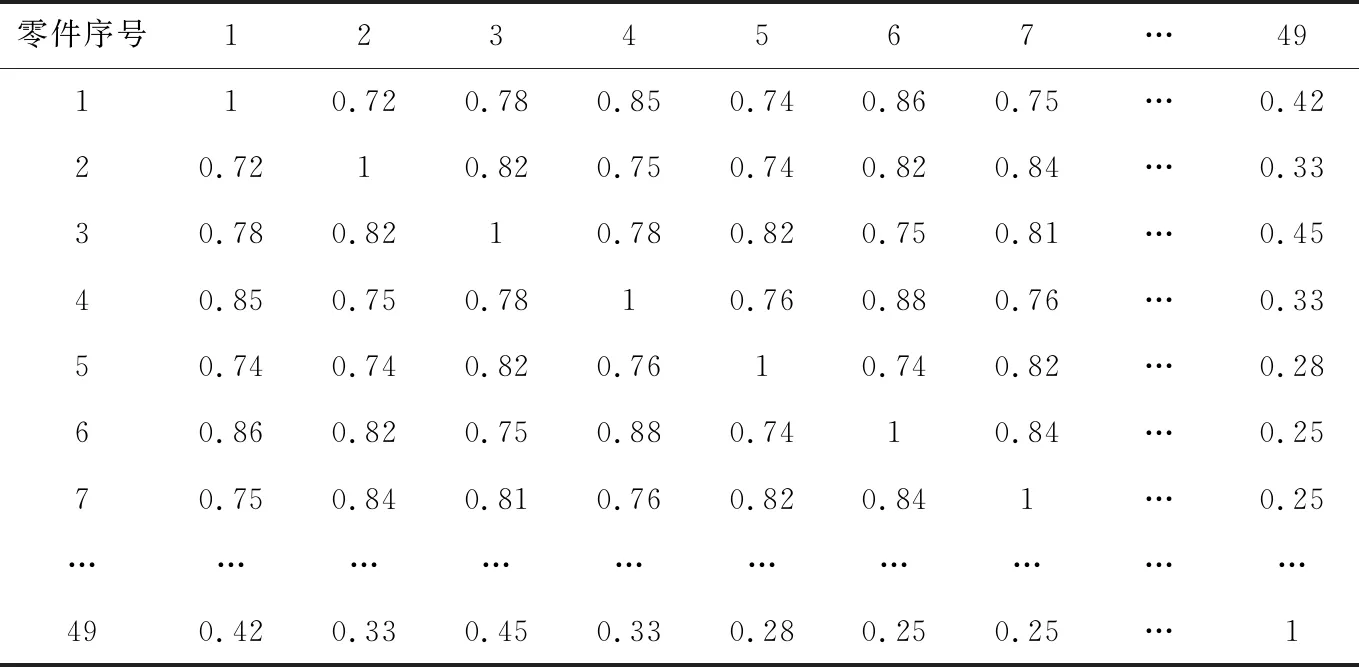
表4 零部件综合关联矩阵

表5 IABC-DPC算法参数设置

为验证改进人工蜂群算法对求解电梯零部件模块划分目标优化问题的有效性，将IABC-DPC算法与人工蜂群(artificial bee colony，ABC)-DPC算法进行比较，记录优化目标函数值和迭代次数，实验结果如图6所示，由图6可以看出，IABC-DPC算法收敛速度明显优于ABC-DPC算法。

图6 算法对比

5 结束语

本文针对产品模块化设计过程中缺乏考虑影响产品改造升级因素，提出了一种考虑改造升级风险的复杂产品模块智能聚类方法，以提高产品改造升级性能。以某升降电梯为例，获得其最优模块划分方案。通过考虑改造升级对产品模块化设计的影响，可使获得的模块划分方案能快速响应外部需求，降低产品改造升级的复杂度。本文为产品改造升级提供了可行的模块化设计思路与方法。