饮用水水质检测中检出限和测定下限的评价方法与合理性判定
2022-06-15邬晶晶宋陆阳朱良琪
邬晶晶,宋陆阳,朱良琪
(中国城市规划设计研究院,北京 100037)
检出限(detection limit,DL)和测定下限(mini-mum quantitation limit,MQL)是水质检测方法中重要的特性指标,其对检测结果的准确度和可靠性有直接影响,进而与环境保护、污染治理、供水安全等依靠水质检测结果判断任务落实质量的工作密切相关。在饮用水检测中,样品中目标物的含量通常较低,检测结果经常处于检出限或测定下限附近,因此,在使用检测方法前,获取适用且合理的检出限和测定下限尤为重要。近年来,诸多研究人员对检出限和测定下限的概念以及评价方法进行了大量的探讨[1-6],但在评价方法的选择上仍存在一定争议。很多检测人员在方法建立或确认时对计算得到的检出限和测定下限通常直接使用,没有进行合理性判定,甚至直接采用标准中给出的检出限和测定下限,容易导致检出限和测定下限与检测工作不适用、不匹配,使检测结果的准确性存在风险。
饮用水检测对检测人员和检测方法的要求较高。为降低检测风险,科学检测水质,保障供水安全,要求检测人员对检测方法的检出限、测定下限等方法特性指标的概念、评价方法及合理性判定有全面清晰的了解。本文将探讨各种检出限评价方法的适用性,提出在饮用水检测方法建立或确认过程中便于确定方法检出限和测定下限的评价方法,并对已获取的方法检出限和测定下限的合理性判定进行详尽的探讨。
1 检出限与测定下限的定义
1.1 检出限
1947年,德国学者Kaiser提出“检出限”这一概念,其强调应将检出限视为分析化学中的一项重要指标,是一种定性概念。《生活饮用水标准检验方法 水质分析质量控制》(GB/T 5750.3—2006)[7]、《环境监测分析方法标准制订技术导则》(HJ 168—2020)[8]、《环境水质监测质量保证手册》[9]、美国环保局(USEPA)[10]等均对检出限具有类似的描述,即在一定置信水平下可从样品中检出待测物质的最小浓度。
检出限还可分为仪器检出限、方法检出限2种类型。其中,仪器检出限即分析化学中仪器设备检测某一待测物浓度的最低限值,方法检出限则是在具体分析方法下目标物以指定置信水平可被测定出的浓度的最低限值。方法检出限的值不是一成不变的,会随着试验环境条件、仪器设备状态、样品处理技术、分析人员操作水平的变化而变化。所以,方法检出限具备可变性特点,需要根据分析化学的试验条件进行适应性确定,在饮用水检测领域一般会使用方法检出限。
1.2 测定下限
测定下限也称为定量限或最低检测质量浓度,是指被测组分的浓度能产生比空白足够大的信号[通常为信噪比(S/N)≥10],这个信号能够被实验室以指定的置信水平在常规操作下定量检出,强调了定量的概念。我国《环境监测分析方法标准制订技术导则》(HJ 168—2020)和USEPA规定,测定下限为方法检出限的4倍。饮用水检测一般使用测定下限(定量限)作为判定标准来出具报告。
2 检出限的评价方法及适用性
2.1 全程序空白标准差法

该方法仅用空白测定结果评估计算检出限,与检测方法中的目标物无关,且只能计算出一个检出限。因此,该方法仅适用于单指标检测方法,对于多指标检测方法并不适用。且在饮用水检测过程中,空白样品中很多情况下都不含有目标物或其浓度极低,多次测定空白时无法计算标准差或只能得到极小的标准差,很难确定合适的检出限。
2.2 净吸光度法
当没有前处理时,分光光度法可以用吸光度(扣除空白)为0.01相对应的浓度为检出限。
2.3 S/N法
S/N为3时对应的浓度为检出限,S/N为10时对应的浓度为测定下限[11-12]。
实际工作中,某些方法如质谱法在检测低浓度样品时,平行测定多次的S/N差别非常大,要获得S/N为3和S/N为10左右的浓度作为检出限和测定下限较为困难,需要进行多次平行测定并结合实际情况综合考虑,以确定适用于检测方法和标准限值的检出限和测定下限。
2.4 统计学方法
统计学方法是基于t分布获得方法检出限的评价方法,是目前饮用水检测领域中一种较为通用的获取方法检出限的评价方法,参照《环境监测分析方法标准制订技术导则》(HJ 168—2020)[8]一般分为空白样品中检出和未检出目标物两种情况。
2.4.1 空白样品中检出目标物
当空白样品中检出目标物时,方法检出限按式(1)计算。
MDL=t(n-1,0.99)×S
(1)
其中:MDL——方法检出限;
n——样品的平行测定次数;
t(n-1,0.99)——自由度为n-1,置信度为99%时的t分布值(单侧);
S——n次平行测定的标准偏差。
本方法计算检出限的前提条件是:测定值之间可允许的差异范围为“空白试验测定值的均值±估计方法检出限的1/2”。
空白试样中检出目标物质时,检出浓度通常不是合适的浓度,使用该方法计算检出限的前提条件大多数情况下都不满足,且在饮用水检测方法建立过程中,空白试验中检出目标物的概率极低,该计算检出限的方法不适用。
2.4.2 空白样品中未检出目标物
对配制浓度为估计方法检出限3~5倍的样品进行n(n≥7)次平行测定,计算标准偏差,按式(1)计算方法检出限。
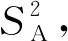
(2)
MDL=t(vA+vB,0.99)×Sp
(3)
其中:vA——方差较大批次的自由度,nA-1;
vB——方差较小批次的自由度,nB-1;
Sp——综合标准偏差;
t(vA+vB,0.99)——自由度为vA+vB,置信度为99%时的t分布值(单侧)。
在饮用水检测方法建立或方法确认过程中,通常使用空白加标的多次平行测定来确定方法检出限,该评价方法的关键在于通过加标获得浓度为估计方法检出限值3~5倍的样品。估计的方法检出限首先通过S/N=3左右来确定,但实际检测过程中低浓度时的S/N存在较大的波动,可能导致加标样品的浓度不是计算出的检出限的3~5倍,需要调整加标浓度重新计算,直到获得正确的检出限。
目标物为多组分的分析方法可以认为是多个单一组分分析方法的组合,需要获得每个单独组分的检出限。与单一组分分析方法的检出限评价方法相同,需要对各个组分进行不同浓度的加标试验、计算、判定等一系列过程,最终确定分析方法中所有组分的检出限,过程极为繁琐。
3 便于确定方法检出限的评价方法
在饮用水检测领域,除比色法、滴定法、称重法、微生物检测等方法以外,绝大部分检测方法都是通过建立各已知浓度与仪器响应值之间的线性关系方程,再代入未知样品的仪器响应值来计算其浓度。常用检出限的评价方法需要通过多次测定其估计值3~5倍浓度的样品,再通过计算获得,即先行估计测定下限附近浓度,但在检测如此低浓度时,仪器响应值的信号波动较大,测定同一浓度的S/N波动也较大。如图1和表1所示,质量浓度均为0.5 μg/L的久效磷测定8次,响应值差别不大,但其S/N波动很大,为12.098~214.251,很难通过S/N=3的方法估计目标物的方法检出限,从而也很难获得所需的加标浓度计算得到目标物的真实方法检出限。随着质谱的普及,高通量的检测方法在饮用水检测领域中也越来越普遍,采用2.4.2小节中的方式评价检出限也将会越来越复杂。
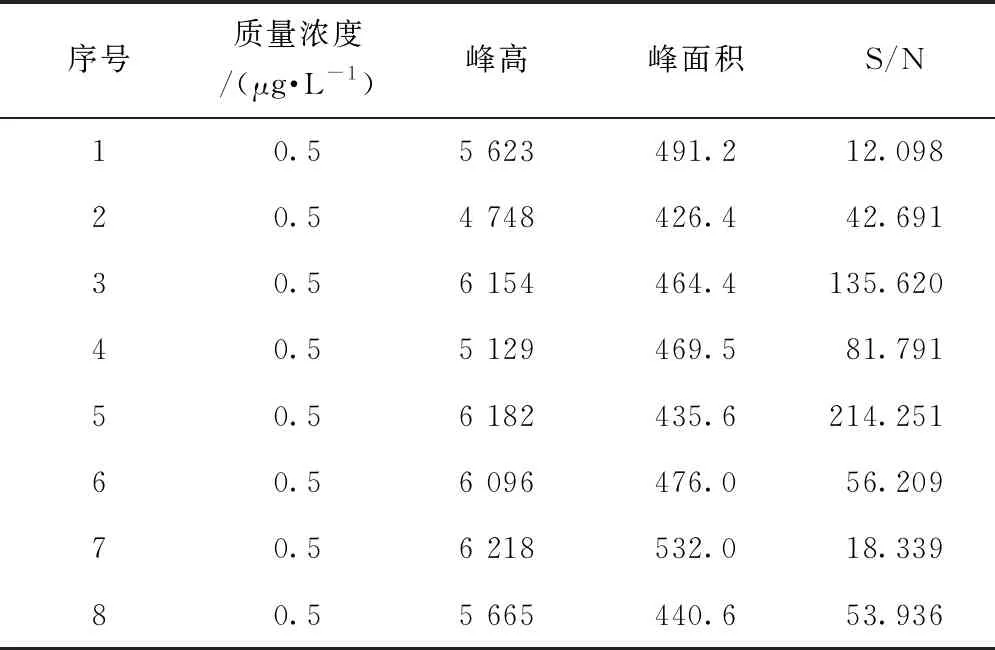
表1 质量浓度为0.5 μg/L的久效磷测定8次的S/N情况

注:223.80>127.00表示定量离子对
统计学方法评价方法检出限的关键在于获得浓度为估计检出限3~5倍的样品,该样品经n次(n≥7)平行测定后通过式(1)计算方法检出限。一般取测定下限为4倍方法检出限,因此,需要的3~5倍检出限浓度即为测定下限附近浓度。理论上校准曲线的最低点浓度应为测定下限浓度,这是检测方法所能准确测定的最小浓度,但测定下限通常不是整数,为了工作方便,制作标准曲线时,最低点通常为略大于测定下限的整数浓度点。因为只有在标准曲线范围内的检测结果才能被认为是准确定量,所以标准曲线最低点的浓度不能超过测定下限太多,否则很容易出现某一目标物浓度大于测定下限,但又在标准曲线之外,造成有检出但不能准确定量的尴尬局面。如某一目标物的测定下限为0.97 μg/L,其标准曲线的最低点一般选为1.00 μg/L。因此,方法检出限和测定下限的确定与标准曲线最低点的确定密不可分,在建立饮用水检测方法时,可将这三者结合考虑。
以《城镇供水水质标准检验方法》(CJ/T 141—2018)[13]中的7.1节液相色谱-串联质谱法检测12种农药为例,便于确定方法检出限、测定下限和标准曲线最低点的操作步骤如下。
①配制相同浓度的12种农药混标,进样优化仪器参数,优化完成后可大致确定各农药的响应情况,可配制一个较低浓度进样观察色谱峰形和响应情况。若混标中各农药响应差别不大,可按照相同浓度配制,若发现溴氰菊酯等农药的响应与其他农药差别很大,可以在配制混合标准样品时适当加大浓度。
②使用步骤①确定后的混标配制多个低质量浓度的样品(0.05、0.10、0.20、0.50、1.00、2.00 μg/L),可根据自身仪器灵敏度进行浓度调整。以农药乐果为例,如图2所示,当配制质量浓度为2.00 μg/L时,其定量离子对的色谱峰形较好,响应较强,进一步配制更低质量浓度,如1.00、0.50、0.20、0.10、0.05 μg/L,可发现浓度越低,响应越低,同时峰形越差。当配制质量浓度为0.05 μg/L时,色谱峰形难以维持,可停止降低浓度。
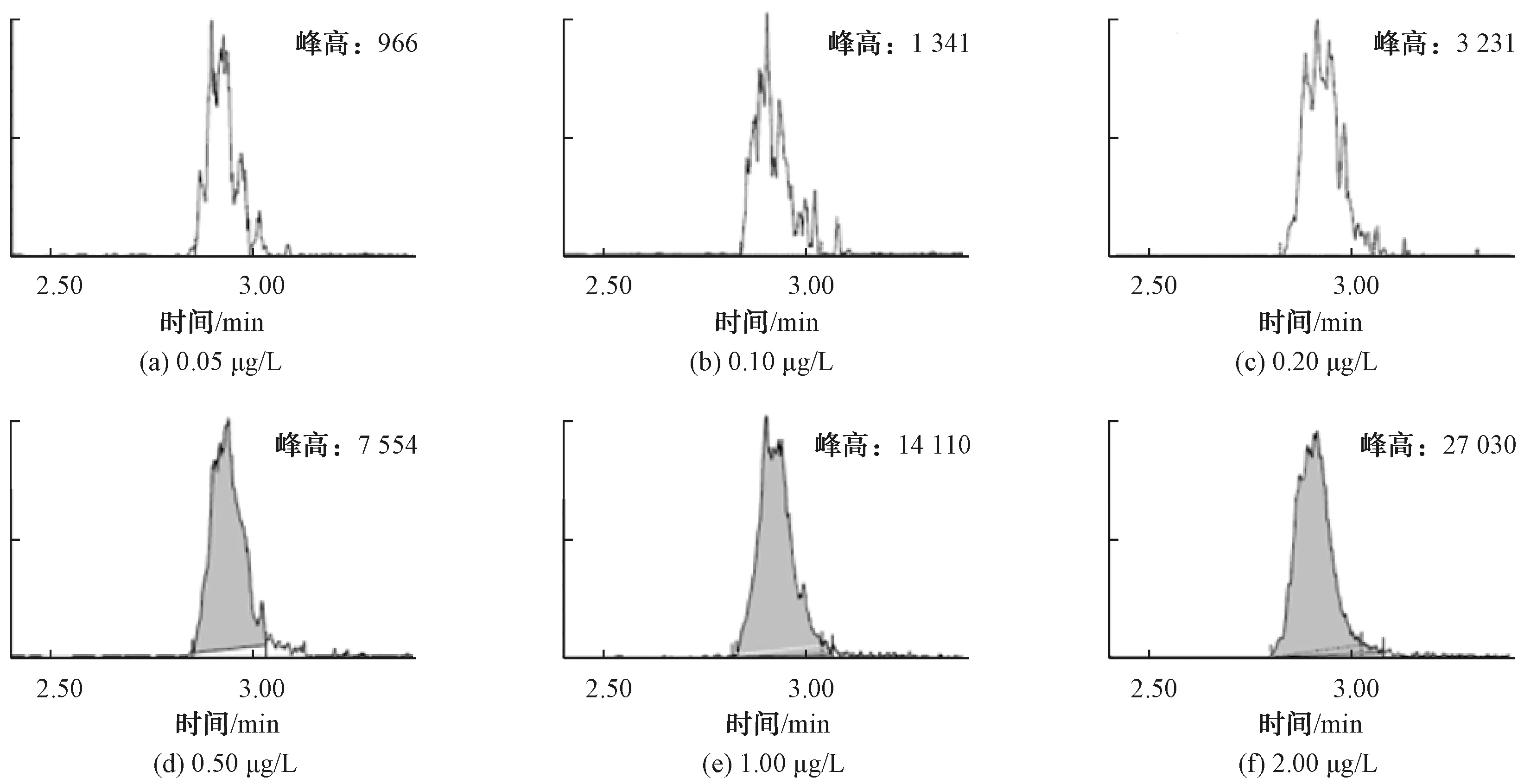
注:230.10>199.04表示定量离子对
③以步骤②中的低浓度点作为标准曲线的低浓度点,同时配制标准曲线中高质量浓度点(5.00、10.00、20.00、50.00、100.00、200.00 μg/L)进样测定,对每种农药进行线性拟合,按照响应情况初步确定各农药标准曲线的最低点和最高点。最低点和最高点由数据处理时的线性拟合情况确定,将无响应信号、S/N低的低浓度点和偏差太大导致线性不良的高浓度点删去,保留中段作为初定标准曲线。
④对配制的所有低浓度点进行7次平行测定,按照浓度从低到高的顺序依次进样,不同浓度之间插入空白,避免干扰。
⑤以步骤③中初步确定的各农药的标准曲线为基准,对步骤④中各农药的低浓度点进行定量,同时观察色谱图,S/N太低时舍弃该浓度点。
⑥对定量后的结果进行数据分析,计算各农药不同浓度点标准偏差S,方法检出限按式(1)计算。方法检出限=3.14×S(置信度为99%时,测定7次的单侧t分布值为3.14),测定下限为4倍方法检出限。此时各农药有响应值的每个浓度点均能计算出对应的方法检出限和测定下限。
⑦对计算出的方法检出限和测定下限进行判定,确定合理的方法检出限和测定下限,判定依据见第4章节。根据确定后的测定下限来确定标准曲线的最低点和线性范围。
本方法以直接进样的高通量液相色谱-串联质谱法作为实际案例展开研究,多个不同低浓度点的样品可直接通过空白基质配制获得。当检测方法存在液液萃取、固相萃取等前处理过程时,若前处理过程影响不大(回收率稳定在80%~120%),可利用空白基质配制多个不同低浓度的平行样,按照本方法确定检出限,再除以浓缩倍数得到最终的方法检出限。若影响较大,应按照样品全程序获得多个不同低浓度的平行样上机测定,再按照本方法确定检出限。
4 方法检出限和测定下限的合理性判定依据
方法检出限和测定下限不是独立的方法特性指标,它们与分析方法的线性范围及标准曲线的绘制紧密相关。如图3所示,理论上分析方法的线性范围应为测定下限到浓度b,为了工作方便,通常取略大于测定下限的浓度a作为线性范围的起点,即标准曲线的最低点。计算得出方法检出限和测定下限必须经过判定,合理的方法检出限和测定下限才能作为方法特性指标使用,否则将大大提高检测风险。
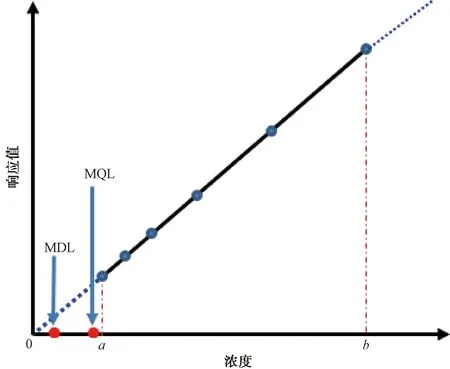
图3 方法检出限、测定下限与线性范围和标准曲线的关系
4.1 依据1:测定下限≤浓度a且尽量接近
浓度a为用于计算方法检出限和测定下限的配制浓度,也是标准曲线的最低点,当测定下限略小于浓度a时,说明浓度a为方法检出限的4倍左右,符合t分布的基本条件。当多次平行测定浓度a后,用式(1)计算出的测定下限>a时,表明浓度a在线性范围之外,即浓度a是不能准确定量的浓度,此时存在一个矛盾,即利用不能准确定量的浓度a,估算出能准确定量的测定下限;当多次平行测定浓度a后,用式(1)计算出的测定下限远小于a时,此时得到的测定下限也不合理,一个原因是此时很容易造成某一浓度大于测定下限有检出,但它在标准曲线之外而不能准确定量的情况,显示数据存在风险,另一个原因是不能保证此时计算出的测定下限具有可准确定量的响应信号(S/N≥10),也不能保证计算出的方法检出限具有稳定可识别信号(S/N≥3)。
例如配制1.00 μg/L的某目标物平行测定7次,计算得到的方法检出限为0.08 μg/L,测定下限为0.32 μg/L,此时测定下限比浓度a小很多,说明平行测定的标准偏差较小,响应稳定,可选择其他浓度点的数据结果。如质量浓度为0.80 μg/L的样品计算得到的方法检出限为0.19 μg/L,测定下限为0.76 μg/L,此时MQL略小于浓度a,观察色谱图,若方法检出限附近浓度具有稳定可识别信号,那么此时的方法检出限和测定下限较为合理。
4.2 依据2:方法检出限附近浓度具有稳定可识别信号
“检出”是指定性检出,即判定样品中存有浓度高于空白的待测物质。因此,方法检出限附近浓度应具有稳定可识别的信号(S/N≥3),若某一浓度条件下计算得到的测定下限满足4.1小节中的判定依据,但其方法检出限附近无稳定可识别信号,那么此时获得的测定下限依然不合理。例如配制0.40 μg/L的某目标物平行测定7次,计算得到的方法检出限为0.09 μg/L,测定下限为0.36 μg/L,测定下限略小于浓度a,但观察色谱图发现方法检出限附近浓度无任何响应,说明计算得到的方法检出限和测定下限不合理,检测时存在假阳性风险。此时需选择更高的浓度点计算后重新判定,直到找到合理的方法检出限和测定下限,进而确定标准曲线的最低点。
若多个浓度点计算出的方法检出限和测定下限均符合4.1、4.2小节中的判定依据,考虑到不确定度的原因,可根据标准限值要求情况,选择稍大的方法检出限和测定下限作为最终的方法特性指标。
5 结论
(1)本文在研究各种检出限和测定下限评价方法适用性的基础上,提出了适用于饮用水检测领域的方法检出限和测定下限的评价方法,该评价方法以实际检测方法的测定范围为导向,将标准曲线最低点与方法的检出限和测定下限相关联,进而得出适用于饮用水检测领域中基于最小二乘法拟合曲线进行目标物分析时合理的检出限和测定下限。同时,本文还提出了判定方法检出限和测定下限合理性的两条依据,即通过测定下限与标准曲线最低质量浓度的关系判定测定下限是否合理,通过检出限附近浓度的响应信号判定检出限是否合理。
(2)对于饮用水中待测物的含量通常较低,特别是有机物项目通常处于痕量分析范围的工况,使用本文提出的检出限和测定下限评价方法,并对其结果进行合理性判定,能够有效降低饮用水检测中有机物项目等痕量分析检测结果的风险,从而达到降低检测风险、科学检测水质、保障饮用水安全的目标。
(3)该评价方法的应用符合我国饮用水水质标准和相关的检测技术不断更新、未来持续更新的新兴污染物的痕量检测要求更高的行业发展趋势,同时随着质谱技术的应用普及,该评价方法也符合高通量检测方法成为主流的检测技术的发展趋势,具有广泛的应用前景。
