变压器寄生参数对LLC 谐振变换器的影响
2022-06-15张平,丁洁,孙莉
张 平,丁 洁,孙 莉
(1. 海军装备部驻上海地区军事代表室,上海 200031;2. 上海船舶设备研究所,上海 200031)
0 引言
随着电力电子变换技术的发展,市场对高开关频率、高效率、高功率密度的电力电子变换器需求越来越广。其中,LLC谐振变换器通过合理的参数设计,能够实现初级侧MOSFET的零电压开通和次级侧整流二极管的零电流关断,从而降低变换器的开关损耗,提高其效率和功率密度,因而得到越来越广泛的应用[1]。
LLC谐振变换器在进行稳态特性分析时,通常对理想变压器进行分析,忽略其寄生参数的影响。而实际应用中,随着开关频率的提高,寄生参数的影响难以忽略[2-3]。
本文对半桥LLC谐振变换器中变压器寄生参数的影响进行了理论分析和试验验证,对半桥LLC谐振变换器的实际应用具有参考意义。
1 半桥LLC 谐振变换器寄生参数
图1为半桥LLC谐振变换器的电路拓扑,包括初级侧开关网络、谐振网络和次级侧整流滤波网络。图1中,Vin为半桥LLC谐振变换器的输入电压,V0为输出电压。开关网络包括两只开关管Q1、Q2及其反并二极管D1、D2;谐振网络包括串联谐振电感Lr、串联谐振电容Cr和并联谐振电感Lm,其中Lr可以用变压器的漏感来实现,Lm可以用变压器的励磁电感来实现;次级侧整流滤波网络包括整流二极管DR1、DR2和输出滤波电容Co,RLd为负载电阻。
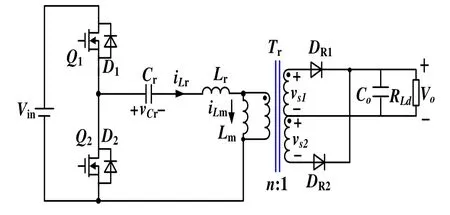
图1 理想半桥LLC 谐振变换器电路拓扑
基波分析法在对谐振变换器进行稳态分析时被广泛应用。故对理想半桥LLC谐振变换器进行稳态分析,得出其稳态模型见图2[4]。图中,Req为等效电阻。
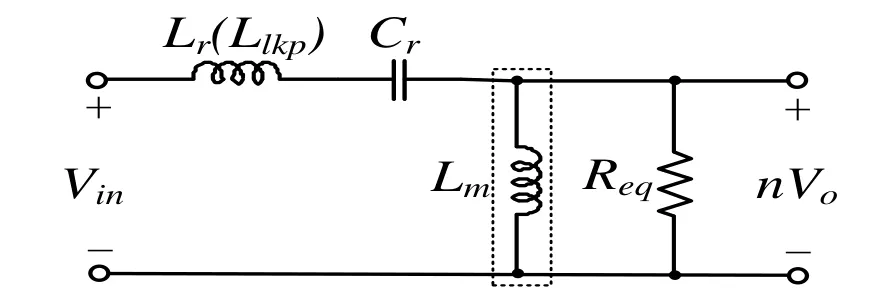
图2 理想半桥LLC 谐振变换器等效模型

此时变换器在不同负载下的增益曲线见图3,其中,fr为变换器谐振频率。当变换器的负载较轻时,最大增益超过1[5]。
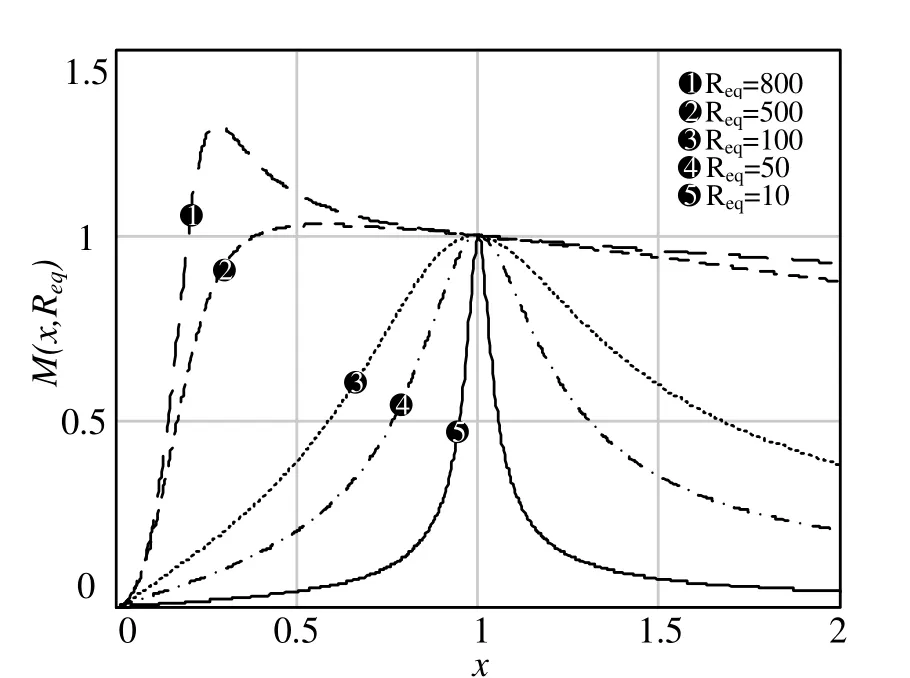
图3 理想半桥变换器的增益曲线
实际上半桥LLC谐振变换器的寄生参数还包括初级侧MOSFET的结电容Coss、次级侧整流二极管结电容Cos、变压器分布电容CTR、变压器初级侧漏感Llkp(可作为谐振电感Lr)以及次级侧漏感Llks1、Llks2,见图4[6]。
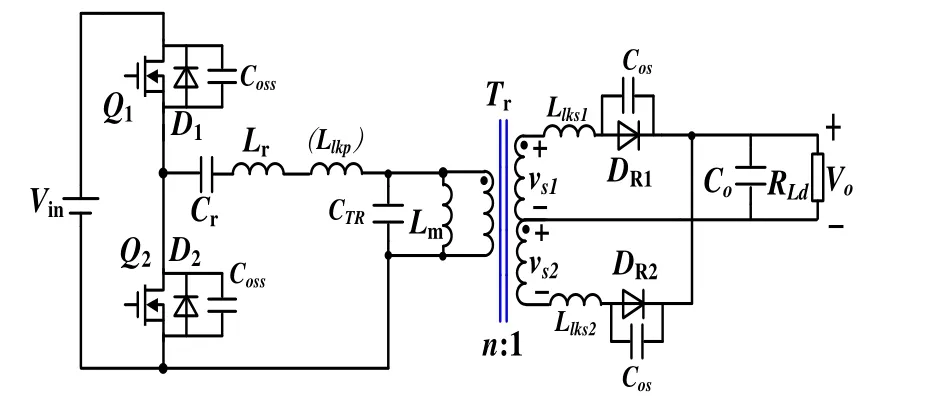
图4 考虑寄生参数的半桥LLC 谐振变换器拓扑
开关器件结电容在器件选型后可确定,本文主要讨论变压器寄生参数对半桥LLC谐振变换器造成的影响。
2 变压器漏感的影响
变压器实际绕制时,初、次级侧均存在漏感,初级侧的漏感可作为谐振电感的一部分,因此,主要考虑变压器的次级侧漏感Ls对变换器特性的影响。
2.1 原理分析
若考虑变压器的次级侧漏感,则变换器的等效模型见图5[7-8]。

图5 考虑次级侧漏感等效模型

式中:Ls为次级侧漏感,μH,折合至原边值为n2Llks。
两个人聊得很少。似乎没有可聊的话题,又似乎话题太多,却总是寻不到进入的切点。只好聊莫高,聊阿芳,静秋说,她现在和阿芳仍然有联系。
作出变换器的增益曲线见图6,可知在考虑变压器的次级侧漏感之后,增益曲线表现为谐振频率点左移,尤其是当负载较重时,曲线的左移更加明显。

图6 考虑变压器漏感的增益曲线
由于本文中分析的半桥LLC谐振变换器采用全波整流方式,变压器次级侧有2个绕组,故对变压器次级侧漏感的影响作进一步分析。
当开关管Q1开通时,其工作模态见图7,谐振电感电流开始以近似正弦规律增大,次级侧二极管DR1导通。此时除谐振电感Lr、谐振电容Cr和励磁电感Lm外,次级侧漏感Llks1也参与谐振。

图7 变换器上管开通时工作模态
而当励磁电感电流线性下降至0之前,开关管Q2开通,其工作模态见图8,谐振电感电流开始以近似正弦规律减小,次级侧二极管DR2导通。此时除谐振电感Lr、谐振电容Cr和励磁电感Lm外,次级侧漏感Llks2也参与谐振。
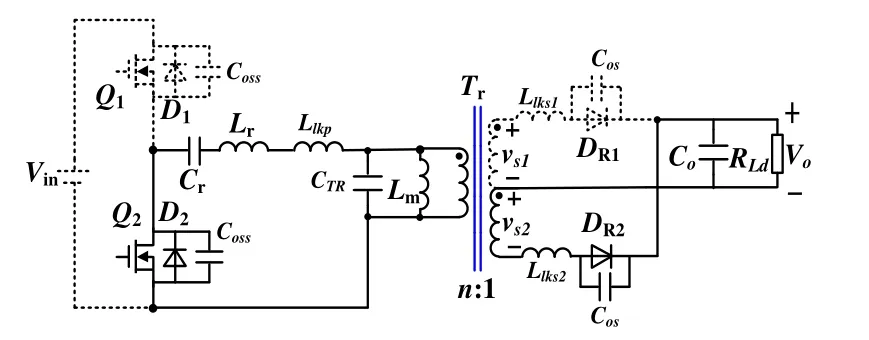
图8 变换器下管开通时工作模态
通过以上分析,可知LLC谐振变换器的变压器次级侧漏感会对变换器的增益和工作模态造成影响,特别是次级侧采用全波整流时,2个绕组存在2个漏感,会在变换器不同工作模态时分别造成影响。
2.2 试验验证
为了验证理论分析的正确性,对半桥LLC谐振变换器进行了开环试验验证。试验条件为:输入电压Vin为680 V,输出电压Vo为150 V,输出功率Po为2kW,工作频率fs为110 kHz,谐振电容200 nF,变压器的励磁电感Lm为406 μH,谐振电感Lr用变压器的漏感来实现[9]。
变压器1采用逐层间绕法,见图9(a),是将初、次级线圈分别绕制在奇数层和偶数层,可在层间加垫绝缘纸,优点是绕制相对简单,且两线圈间耐压较高,缺点是初、次级的耦合相对较差。

图9 变压器绕制方式
变压器1的初级侧漏感为4.975 μH,次级侧漏感分别为3.53 μH、1.44 μH。
采用变压器1时,谐振电感电流波形如图10所示。由图10可知,变压器次级侧2个绕组漏感不一致时,会导致不同工作模态时谐振频率不同,谐振电感电流波形正负半周不对称。
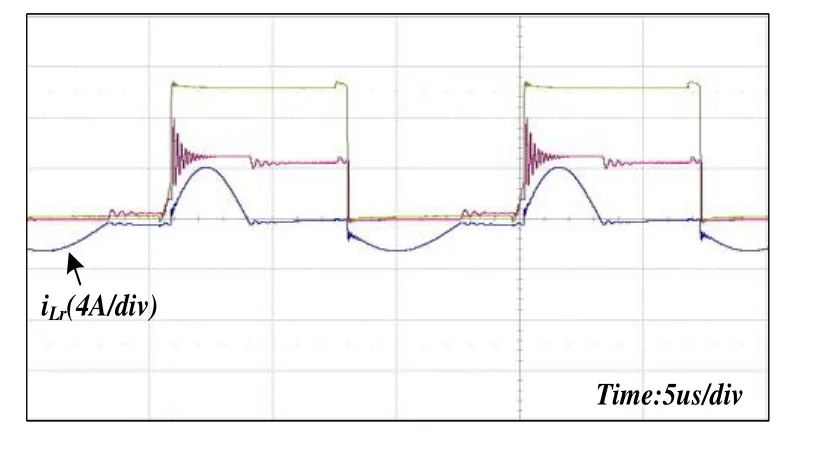
图10 采用变压器1 时的波形
变压器2采用夹层式绕法,如图9(b)所示,即三明治绕法,是指将初级绕组分成2部分,先绕制一半,接着绕制次级线圈,最后再绕制初级线圈的另一半。这种方法增大了初级与次级的有效耦合面积,减小了变压器漏感,同时由于在初级绕组间加入次级绕组,也减小了初级绕组的层间分布电容,且只在初级绕组中多一个接头,工艺简单,便于批量生产。
变压器2的初级侧漏感为6.81 μH,次级侧漏感分别为0.83 μH、0.83 μH。采用变压器2时,谐振电感电流波形见图11。由图11可知:变压器次级侧2个绕组漏感基本一致,谐振频率基本一致,谐振电感电流波形正负半周对称。
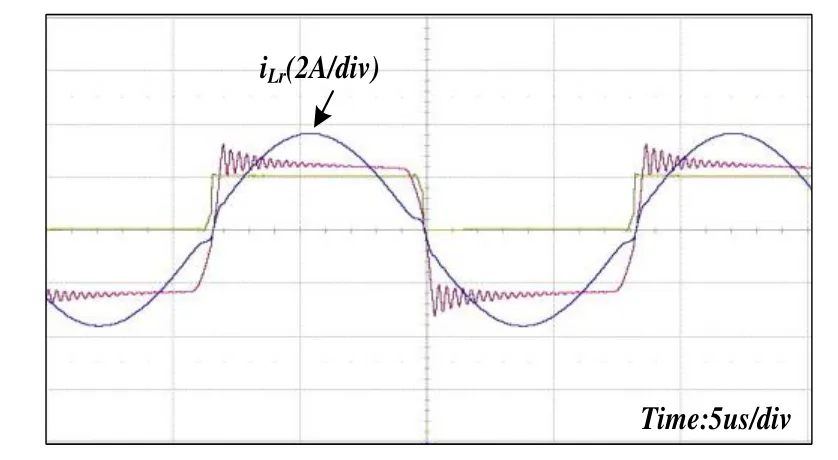
图11 采用变压器2 时的波形
故半桥LLC谐振变换器采用全波整流方式时,需特别注意变压器的绕制方式,保持次级侧2个漏感一致。
3 变压器分布电容的影响
变压器的分布电容在实际绕制中也不可避免,主要分为绕组匝间电容、层间电容、绕组电容和杂散电容等。
3.1 原理分析
考虑变换器的分布电容,变换器的等效电路见图12。

图12 考虑分布电容等效模型

式中:CTr为变压器分布电容,pF。
根据式(3)作出增益曲线见图13。一般情况下,变压器的分布电容为pF级。根据增益曲线可以看出,变压器的分布电容会造成变换器在低频段的增益下降以及高频段的增益曲线上抬。特别是在负载较轻时,分布电容的影响会更严重。

图13 考虑变压器寄生电感、分布电容增益曲线
3.2 试验验证
为了验证变压器分布电容的影响,在空载情况下,对半桥LLC谐振变换器试验验证。试验条件为:输入电压Vin为680 V,输出电压Vo为150 V,输出功率Po为2 kW,工作频率fs为110 kHz,谐振电容200 nF,变压器的励磁电感Lm为406 μH,谐振电感Lr即初级侧漏感为6.81 μH,次级侧漏感均为0.83 μH。
当变压器分布电容较大时,由于分布电容参与谐振,空载时谐振电感电流、次级侧二极管电压波形见图14,振荡严重。

图14 分布电容较大时空载波形
虽然变压器分布电容不可避免,但可通过以下途径减小其大小:
1)通过选择介电常数较低的漆包线、增大绕组匝间的距离、多槽骨架分段绕制减小绕组匝间电容。
2)通过增大绕组层间距离(如:采用三重绝缘线)、选择绕线面积较宽的骨架、采用交叉堆叠绕法来减小层间电容。
3)通过增加绝缘厚度、增加法拉第屏蔽层来减小绕组电容。
根据以上途径将变压器分布电容减小后,空载时谐振电感电流、次级侧二极管电压波形见图15,其造成的谐振明显减小。
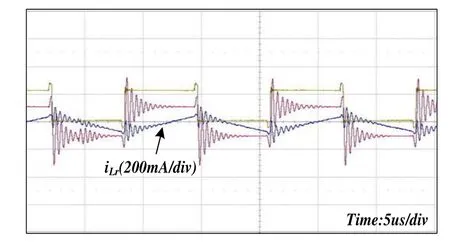
图15 分布电容较小时空载波形
4 结论
针对LLC谐振变换器在进行稳态特性分析时,通常对理想变压器进行分析,忽略其寄生参数的影响的问题,本文对LLC谐振变换器中的变压器寄生参数造成的影响进行了理论分析和试验验证,对LLC谐振变换器的实际应用具有参考意义。
