船用脱硫系统导流装置流场和阻力特性

卞修涛，蔡乾亚，陈 乐，罗亚萍，缪文杰

（江南造船（集团）有限责任公司，上海 201913）

0 引言

船舶海运占国际贸易总量的90%，其巨大的货物运输量也带来了严重的环境污染问题，数据表明船舶行业NOX排放量占全球总量的10%，SOX排放量占总量的3%[1]；随着国际贸易量的逐年增长，船舶行业对气候的影响将愈加明显。关于海洋船舶酸性气体排放问题，已有多种脱硫方法[2-3]，其中一种有效且广泛使用的方法是在船舶排气系统中加装脱硫装置[4-5]，将原排放至大气的酸性气体进行洗涤后部分或全部排入海中。针对该部分酸性洗涤水，考虑到近海环境污染问题，多国已出台规定并限制船舶排放洗涤水的pH值，因此，在船用脱硫系统出口处加装导流装置十分必要，能够降低洗涤水排出后的流速和压力，增强酸性洗涤水与弱碱性海水掺混，确保酸性洗涤水排放达标。

当前，多种船用脱硫系统已加装各类导流装置，但不同流动工况下的装置压损特性尚不明确，因此，多数脱硫系统管路布置仍使用能量富裕的方式，以弥补导流装置对流动的阻滞作用，而这必将导致船舶管路系统额外的能量损耗，且管路流体能量富裕不利于洗涤水与海水掺混。相比于试验方法，数值求解方法能够快速获取高精度计算结果，但采用三维计算流体力学（Computational Fluid Dynamics，CFD）方法获取脱硫系统管路阻力受到计算资源限制，其中，脱硫系统整体管路全三维CFD计算需要巨大的网格量支撑，且不同流动工况下的大量CFD计算将耗费巨大的计算资源。此外，脱硫系统一维管网计算虽然对计算资源要求较低，但缺少不同流动条件下导流装置的压力损失或损失系数而无法进行。因此，为合理设置脱硫系统管路流量和压力等参数，有必要对导流装置流场和阻力特性进行分析。

基于上述问题，本文结合一维管网分析方法计算资源需求量低和三维数值模拟方法计算结果精度高的优势，对照阀门等管路部件损失系数变化特性，研究导流装置流场和阻力特性，获取装置局部总压损失系数，为脱硫系统压力-流量关系匹配提供基础，为脱硫系统管路布置提供指导。

1 数值方法

1.1 几何模型和边界条件

导流装置几何模型见图1。已有多艘船舶安装该导流装置，为详细分析其内部流场特性，本文计算域忽略真实管路中弯头等装置影响。为能够获取稳定、可靠的计算结果，以出口管径作为特征长度，入口截面位于导流装置上游1倍管径处，出口截面位于装置下游3倍管径处。

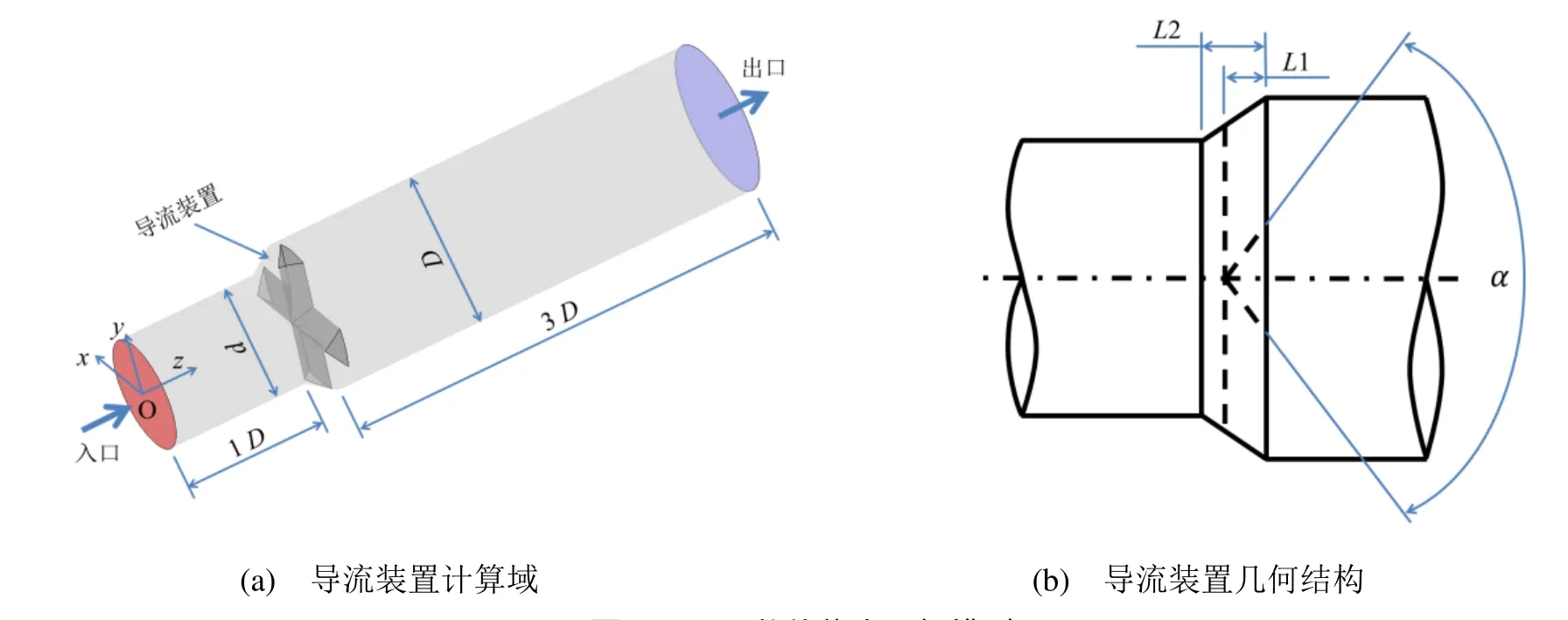
图1 CFD 数值仿真几何模型

对于管内流动仿真，使用图1(a)所示坐标系，其中z为流动方向，x为导流器侧视图方向，y为竖直方向，同时，x和y坐标方向与导流装置几何结构存在平行关系。导流装置具体几何结构在图1(b)中给出，导流装置位于管路扩张段，由截面为等腰三角形的2个三棱柱相交构成，等腰三角形夹角α为106°，其他几何参数见表1。

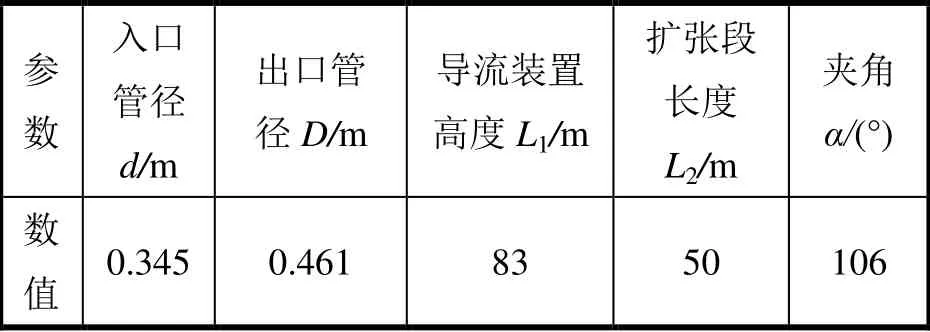
表1 几何参数

在实船设计中，导流装置靠近脱硫系统管路出口，其具体位置如图2(a)所示，设计工况下，每个出口所通过平均质量流量为125 kg/s，船舶运行时管路出口位于水下2 m处，因而图1(a)计算域CFD仿真中出口设置为压力边界条件，给定相对压力为1.95×104Pa。

图2 边界条件求解方案

由于受到脱硫系统整体管路流动影响，图1(a)计算域入口处总压参数难以获取，CFD计算入口处需给定质量流量边界。

脱硫系统管路整体通流能力采用一维管网计算方法进行求解，计算软件选取为Applied Flow Technology公司的Fathom 9模块，其管网阻力分析模型在图2(b)中给出，图中P1～P8为各段管道结构，J1表征流动入口，该系统中管路入口与脱硫塔出口相连，J8和J9表征流动出口，位于水下2 m处，J2、J4和J5为变径段，J3为连接三通，J6和J7为管路阀件。

在图1(b)所示的扩张段处，导流装置的存在使流动通流面积变为圆管面积的1/3，且装置交叉点位于管道主流区，假定导流装置节流效应明显，局部总压损失设置为10 kPa。

管网计算结果表明，图2(a)中脱硫系统管路极限质量流量可设置为209 kg/s，为研究不同流动工况下导流装置的局部阻力系数，入口边界条件设置如表2所示。图1(a)中导流装置计算域所有壁面均采用无滑移边界条件。

1.2 湍流模型及网格设置

求解器采用商用软件Simcenter STAR-CCM+12.02，数值求解在并行计算集群中实现，表2中结果表明管路入口雷诺数均在105量级，参考管路阀门流场与阻力特性计算方法[6-7]并结合软件功能，湍流求解选用雷诺平均方法中可实现的k-ε湍流模型。

表2 局部阻力系数工况入口边界设置

为保证计算结果具有较高准确度，全局采用多面体网格，考虑网格布局展示的清晰度，以10万网格为例进行展示，结果见图3，固体壁面使用棱柱层网格生成方法以形成边界层网格，网格加密过程中，边界层网格和全局网格同时进行均匀加密。在图1(a)所示计算域中，沿坐标轴z方向选用距离出口0.5D位置处截面作为特征截面，以该截面质量流量平均后的总压结果作为特征参数，分析网格无关性，质量流量平均过程在式（1）中给出。

图3 网格划分（10 万网格单元）

式中：w为坐标z方向速度；ρ为流体密度；dξ为面微元或线微元；ϕ为物理量ϕ的质量流量平均结果。网格无关性验证结果见图4，当全局网格加密至73万时，出口特征截面处总压参数已基本保持不变，后续计算将采用73万网格进行。

图4 网格无关性验证

2 导流装置流场与阻力分析

2.1 流场分析

图5为设计工况下流场流线分布结果，导流装置对流场产生剧烈扰动，流体流经导流装置后形成多个的漩涡，漩涡影响区域较大，对流动产生阻滞作用。由于设计工况下流场整体流动速度相对较低，导流装置节流作用对速度幅值影响有限。

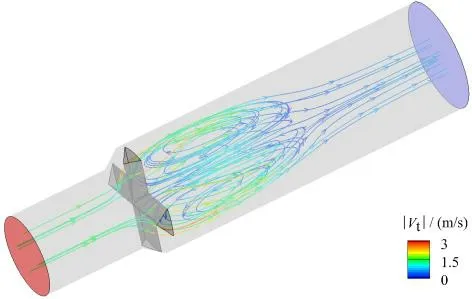
图5 设计工况流场流线分布

图6为中截面处流场总压分布。由图6可知：导流装置的节流效果对流场总压影响十分明显，在节流装置后形成一个双峰低压区，相比于入口位置，出口截面处总压参数相对较低，出口处流体总压参数降低有利于缩小酸性洗涤水的影响区域，降低酸性洗涤水对航行海域的影响，确保脱硫系统洗涤水排放达标。

图7为x=0.3D处流场总压分布结果，相比于图6中的结果，靠近流场出口处总压较低，主要由于受到管壁边界层影响，总压损失较高；同时，流场下游低压区的双峰现象减弱，主要由于流动远离导流装置几何交叉点，远离涡结构核心区，受到竖直方向导流装置的影响减弱，在后续流动研究中可对导流装置进行优化，进一步增大导流装置处的压降。

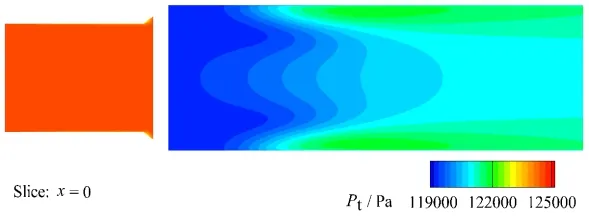
图6 总压分布，x=0

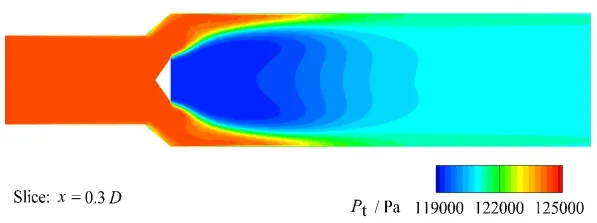
图7 总压分布，x=0.3D

2.2 阻力分析

在图1(a)的计算域中沿坐标轴z方向，以距离入口和出口0.5D位置作特征截面，应用总压损失系数ζ表征导流装置局部阻力特性，其计算过程在式（2）中给出，其中：ΔPt为入口特征截面和出口特征截面总压差；另外，以入口特征截面处面质量流量平均后的密度及速度幅值作为特征参数，对总压损失进行无量纲化。

做出不同质量流量入口条件下导流装置阻力特性结果见图8，图8(a)为导流装置总压损失随质量流量变化结果，对于本文特定几何模型的不可压缩流动而言，图8中的总压损失随质量流量呈指数关系变化，符合损失和流速的平方关系理论，也表明了计算结果的可靠性。

图8(b)为导流装置总压损失系数ζ随无量纲雷诺数变化特性曲线，总体而言，导流装置总压损失系数随雷诺数变化较小。在选取工况条件下，装置总压损失系数变化区间为[3.64, 3.70]，若以3.64为基准，其相对变化幅度为1.6%，在后续管网分析中可调用导流装置总压损失系数3.64用于管路阻力计算。此外，导流装置损失系数随雷诺数增大的变化关系为先降低后逐渐趋向平稳，若将导流装置和阀门归于管路通用元件，其局部损失系数随雷诺数变化曲线与电磁阀基本一致[8]，也相应表明计算结果的合理性。

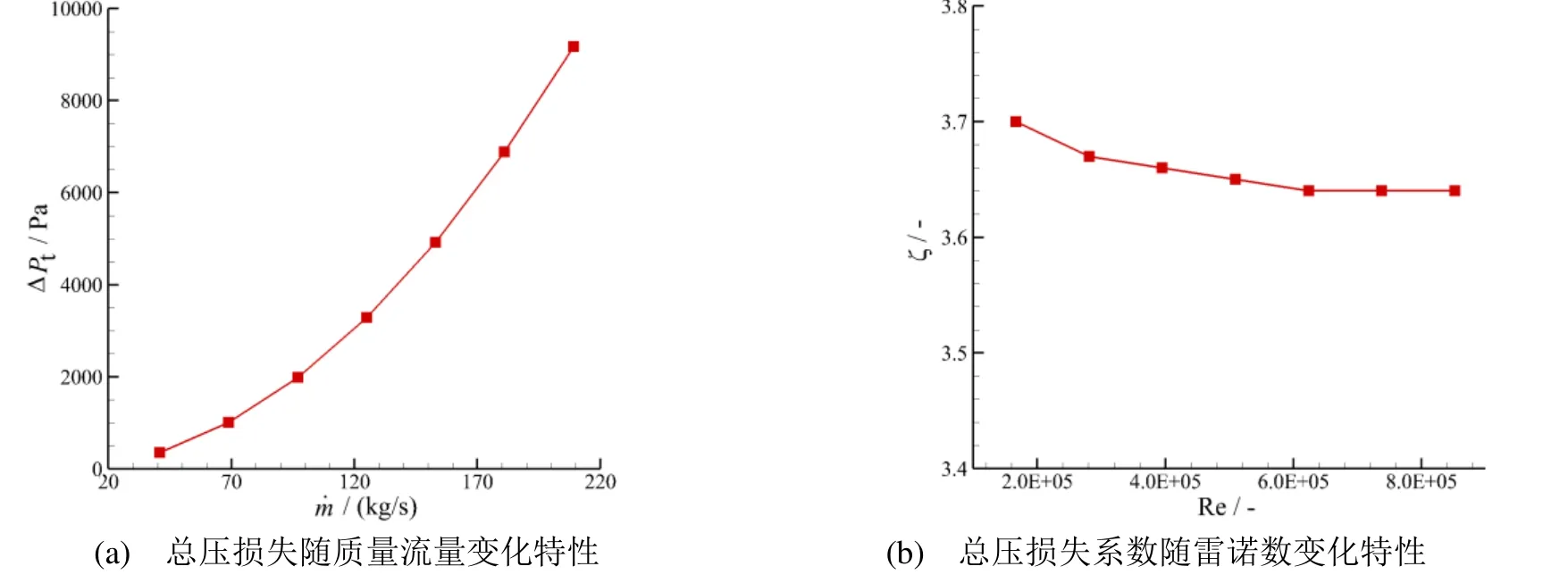
图8 流动损失随来流参数变化特性

3 结论

本文结合一维管网分析方法和三维数值模拟方法计算优势，研究典型导流装置流场与阻力特性，结果表明导流装置节流效应明显，可显著降低管路流场总压；在选取的流量范围内，装置总压损失系数幅值随雷诺数变化幅度较小；管网计算分析中可将该导流装置总压损失系数设置为3.64。针对导流装置结构模型及本文计算结果的可靠性，后续可相应优化并采用PIV等试验方法进一步验证计算结果。