有关里卡蒂方程的系统研究

张玮玮

（安庆师范大学 数理学院，安徽 安庆 246133）

反映客观世界运动过程中量与量之间的关系可以用常微分方程关系式进行描述，因此，需要通过求解常微分方程来了解未知函数的关系。常微分方程属于数学分析的一支，是数学与应用密切相关的基础学科。关于常微分方程的求解，希望能用初等函数或超越函数表示其解，即求通解。莱布尼兹（Leibniz）曾专门研究利用变量变换解决一阶微分方程的求解问题，欧拉（Euler）则试图用积分因子统一处理，其中，伯努利（Bernoulli）、里卡蒂（Riccati）微分方程就是在研究初等积分时被提出、后人以他们的名字命名的方程[1]。然而，能用初等解法解决的微分方程是有限的，绝大部分微分方程是没有解析解的，或者还没有有效的方法求其解析解，譬如形式简单的里卡蒂方程。除了少数情况外，里卡蒂方程没有初等解法，这一事实在1841年被法国数学家刘维尔（Liouville）证明。于是，人们寻求别的方法来研究微分方程问题[2]。

里卡蒂方程是一类特殊的微分方程，在流体力学和弹性振动等领域有着重要应用。1724年，数学家里卡蒂首次给出了该方程的特殊形式，并受到学者关注[3]。由于里卡蒂方程在理论和实际中都有着一定的重要性，对此类方程通解的求法一直被广大学者重视[4-9]。例如，王明建等利用初等方法研究一类特型Riccati微分方程有解的充要条件，并得到了Riccati方程的通解[7]；倪华等讨论了通过变量变换来求几类里卡蒂方程的通解[8]；戴伟等介绍了含有指数函数的Riccati微分方程通解的求法[9]。以上讨论的都是当方程满足一定条件下的里卡蒂方程的特解及通解的求法。但除了这些特殊情况外，现有文献还未见其他特殊类型的里卡蒂方程的求解方法。为弥足这一不足，本文研究三种特殊形式的里卡蒂方程特解求法（这一方程的系数函数之间有特殊内在关系），并借助初等变换得到此方程的通解，从而在不给出特解的情形下求其通解，丰富了里卡蒂方程的通解理论。

1 预备知识

里卡蒂方程的一般形式为

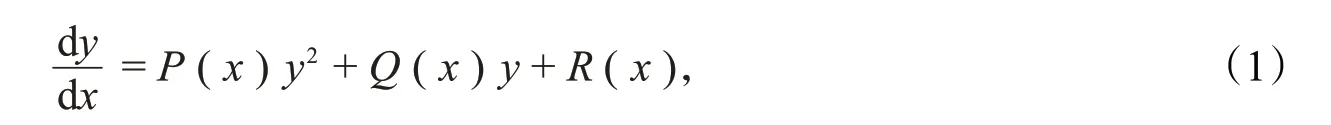
其中，P(x),Q(x),R(x)为x的连续函数。

虽然方程（1）的形式很简单，但其通解并不能用初等解法求解。如果已知方程（1）的一个特解，那么通过变量变换，先将方程（1）转变为伯努利方程，再进一步转化成线性方程来求通解。事实上，在已知一个特解的前提下，可以直接将方程（1）化为一阶线性方程来求解。

然而，对于方程（1）特解的求解也并非易事，技巧性很强。现研究当里卡蒂方程的系数函数P(x),Q(x),R(x)满足一些特殊条件时，其特解及通解的求法，并研究在不求特解的前提下，如何求其通解。

2 主要结论与证明

首先讨论三种特殊类型的里卡蒂方程特解的求法，给出特解的具体表达式，从而得到其通解。

3 应用举例与总结

下面通过实例来分别说明上述方法的应用。

解对照方程（1）的形式，P(x)=e-2x,Q(x)=1,R(x)=-1，显然符合类型2的情形。根据定理2得到(x)=ex，是该方程的一个特解。下面求其通解。设原方程的解为y(x)=z(x )+e（x其中z(x)为待定的未知函数），代入原方程中可得：

总之，里卡蒂方程通解的求法是一个开放性的课题。当系数函数满足特殊条件时，先给出特解的一般形式，进而求其通解。在不给出特解的情形下，当方程的系数函数满足一定条件时，可直接写出通解。以上实例说明了这些方法的正确性和有效性，为今后研究里卡蒂方程的求解提供了新思路。在研究这类问题时，要注意解题技巧，要善于总结经验，注意解题的灵活性，根据方程特点，作适当的变换，将方程化为能求解的新类型，进而求解。