基于集成ARIMA模型与BP神经网络的锂电池容量预测

张朝龙，卢 阳，杨 璇，胡靓靓

（安庆师范大学 电子工程与智能制造学院，安徽 安庆 246113）

新能源汽车对电池性能要求日益增强，动力电池储能技术的健康管理尤为重要，所以只有及时对锂电池进行性能检测和剩余容量预测才能更好地保障设备正常运行，避免发生严重的事故[1]。现阶段锂电池容量预测方法主要分为两大类[2-6]：电池物理失效模型法[2-4]和数据驱动法[5-6]。基于模型方法需要分析被测对象的性能下降和失效机制，从而建立被测对象的数学物理模型。锂电池系统复杂，其噪声、数据的可用性、不确定的环境变化及约束等，使得为锂电池性能下降过程建立一个精确表征并普遍适用的数学物理模型并不容易，故该方法不适于电池容量预测。数据驱动方法是通过机器学习来分析被测对象的性能数据，进而进行预测，该方法无需了解对象的运行机制，适用性强。其中，反向传播（BP）神经网络是一种经典的数据驱动方法[7-8]，可用于电池容量预测。BP神经网络具有自组织、自学习以及对于输入数据和规则的鲁棒容错能力，但受数据影响较大。而差分整合移动平均自回归（ARIMA）[9-10]属于线性预测模型，对于解决多元线性问题有明显优势，有非常强的预测、分析数据能力。故本文推出ARIMA与BP神经网络集成的方式，先利用ARIMA预测前期电池的容量，再通过BP神经网络自学习来预测电池后期的剩余使用寿命，从而实现锂电池剩余容量的精确预测。

1 ARIMA算法与BP神经网络集成工作原理

时间序列主要由时间要素和数值要素组成，由此分为时期时间序列和时点时间序列。这两种序列的区别在于前者中不同时期的观测值可以相加，相加结果可表明现象在更长一段时间内的活动总量，而后者的相加结果没有意义，不能相加。

时间序列的数值变化规律主要分为长期变动趋势、季节变动规律、周期变动规律和不规则变动，这4种变动也就是时间序列数值变化的分解结果。时间序列中可能会同时出现这4种变动，也可能只出现一种或者几种，这种不确定性由引起各种变动的影响因素所决定。4种变动和指标数值的变动关系可能是叠加关系，也可能是乘积关系，这取决于随着时间的推移时间序列图是否存在季节波动。对数据进行差分处理，转换为平稳的时间序列后再进行建模，ARIMA(p,d,q)模型为

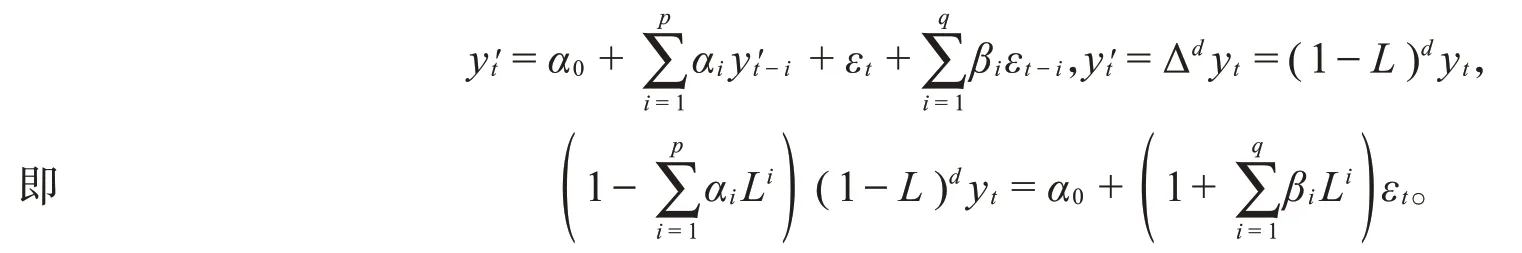
其中，y为预测值，α为增长率，β为平均误差率，L为实际值。

非线性变化单元组成的前馈型人工神经网络，简称为BP网络。以二层网络为例，有n个输入，m个输出，两个中间层；输入结点、中间结点和输出结点分别用i、h、j表示；由输入结果i到中间层h结点的权值用Wih表示；由中间层结点h到输出层结点j的权值用Whj表示。对于输出数据，设其目标输出为d，实际输出为y。

2 实验结果和讨论

电池充放电数据来源于安庆师范大学新能源汽车动力电池测试实验室。实验室使用的是18650电池，其中，18表示直径为18 mm，65表示长度为65 mm，0表示为圆柱形电池。使用新威电池检测装置在1 C充电、1 C放电、25°C恒温条件下进行测试。

将前400组电池充放电数据导入SPSS，通过专家模拟器可知最优模型为ARIMA（1，1，14），该模型预测结果如下页图1所示。前期、中期和后期模型统计见下页表1。利用迪基-福勒（DF）检验可以测试自回归模型是否存在单位根。模型的残差AFC与残差PAFC结果如下页图2所示。

图1 ARIMA模型前期预测结果

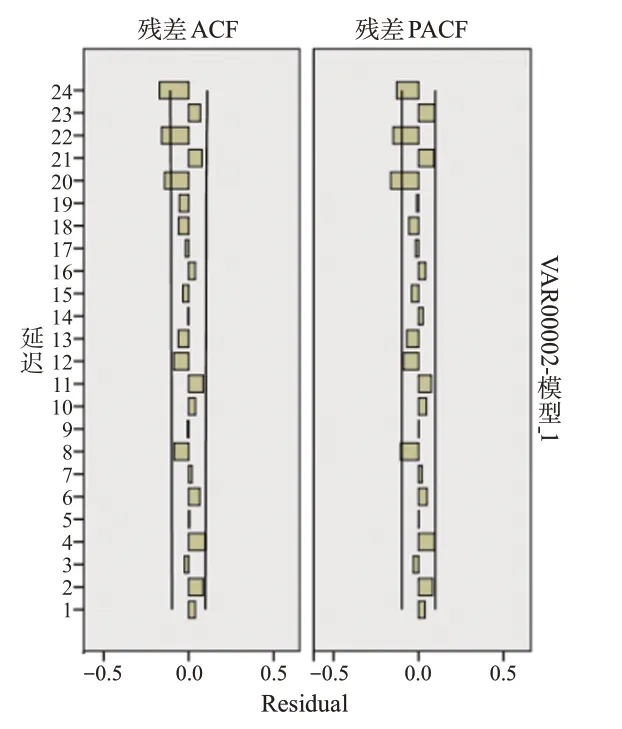
图2 前期残差AFC与残差PAFC

由表1可知，前期模型显著性大于0.05，故残差均可认为是白噪声，证明该模型有效，预测结果也有效。随后将中期501到1 000组的数据导入SPSS，进行时间序列分析，得到最优模型为ARIMA（0，1，9），残差如图3所示。由表1和图3可知该模型预测效果有效，ARIMA模型中期预测结果如图4所示。对后期数据进行预测发现有大量离群值，故无法用ARIMA模型进行预测。由表1可知，后期模型显著性为0，小于0.05，效果不理想，则后期采用BP神经网络进行预测。利用MATLAB语言编写BP神经网络算法程序来分析已有数据，发现电池放电容量一直呈下降趋势，为了使神经网络得到足够的学习，将后期数据中前420组充放电数据当作训练集，后80组充放电数据当作检验集。通过调整隐层神经元数目、训练次数和训练误差上限，本组获得了令人满意的结果。

图3 中期残差图

图4 ARIMA模型中期预测结果

表1 模型统计表

将训练好的网络代入校验集，对后80组充放电数据进行校验，如下页图5所示，样本值和校验值虽然存在一定偏差，但是变化趋势一致，因此该神经网络模型通过样本集的训练，可以对未来一段时间的电池剩余容量进行预测。预测偏差虽不能通过增加样本量来消除，但可以减小。在训练过程中，反向传播对于参数的更新会出现内存溢出或其他数值存储上的微小误差，故偏差不可能不存在，只能更加接近其真实值。

图5 实际值与预测值对比

本组数据进行了38次迭代，最佳模型于32次迭代时出现，如下页图6所示，对应于最小的均方误差。将拟合值与真实值进行回归，其中回归值R表示测量输出和目标之间的相关性。R值为1表示密切关系，0表示随机关系。如下页图7所示，R值几乎都接近于1，可见拟合效果非常好。

图6 模型最佳迭代次数

图7 真实值与预测值拟合效果

3 结论

综上所述，本文提出了一种集成ARIMA与BP神经网络集成来预测电池容量的方法。相比传统的ARIMA模型，加入BP神经网络可以解决其长期预测失效问题，且保持了ARIMA模型的泛化适应性、通用性等优点，两模型中的数据显著性均大于0.05，可认为残差是白噪声，预测值也在置信区间中，预测效果较好。本文提出的方法及研究结果对今后锂离子电池容量研究具有一定的参考与借鉴意义。