热传导方程初值问题解的最大模估计的教学探讨

陈正争，施敏加

（安徽大学 数学科学学院，安徽 合肥 230601）

偏微分方程理论是在解决物理学、力学和工程技术等领域问题基础上发展起来的一门科学，是数学的一个重要分支，它不仅促进了许多自然科学和工程技术问题的解决，还促进了泛函分析、微分几何、复变函数和计算数学等数学分支的发展，表现出强大的生命力。“偏微分方程”这门课通过三类典型的偏微分方程（即波动方程、热传导方程和位势方程）的导出、定解问题的求解以及解的性质探讨让学生掌握偏微分方程的基本理论、方法和技巧，以期培养学生的理性思维品质以及分析和解决实际问题的能力，为后续课程的学习或者从事相关工作奠定基础。

“偏微分方程”课程是国内众多高等院校应用数学和计算数学专业本科生的一门专业基础课，也是物理、力学和土木等理工科专业本科生或研究生的一门专业必修课。其中，热传导方程的初值问题是“偏微分方程”中重要且较难的知识模块，尤其是，关于该问题解的最大模估计是教学的一个难点，其主要原因在于证明过程的技巧性很强。针对此问题的处理，多数教材[1-5]都是先讨论热传导方程初边值问题的极值原理，然后通过构造一些辅助函数将初值问题转化为初边值问题，再利用初边值问题的极值原理来讨论初值问题解的最大模估计。形式特殊的辅助函数构造导致热传导方程初值问题解的最大模估计的证明过程技巧性很强，从而使学生难以理解和掌握。因此，在实际教学过程中，寻求新的简单证明方法对于热传导方程初值问题解的最大模估计的教学具有重要意义。

基于以上分析，本文尝试不通过构造任何辅助函数，也不利用热传导方程初边值问题的极值原理，而仅用基本的分析方法给出一类热传导方程初值问题解的最大模估计的一个简单证明，以化解难点。并利用该方法，进一步探讨具有一般形式的二阶线性抛物型方程初值问题解的最大模估计。

1 一类热传导方程初值问题解的最大模估计的简单证明

在带形区域QT={(x,t)|-∞＜x＜+∞,0＜t≤T}上考虑如下热传导方程的初值问题：

2 一类二阶线性抛物型方程初值问题解的最大模估计

考虑如下一般形式的二阶线性抛物型方程初值问题：

注记2文献[1]的作者通过构造特殊的辅助函数，再利用有界区域上二阶线性抛物型方程初边值问题的极值原理来证明定理2。与文献[1]中的相应结果和方法相比，我们不需要构造任何辅助函数以及利用初边值问题的极值原理，而仅用基本的分析方法证明了定理2；此外，文献[1]中要求函数b(x,t)满足|b(x,t)|≤b0，其中，b0＞0为某个正常数，而在我们的结果中不需要b(x,t)的这一限定性假设。

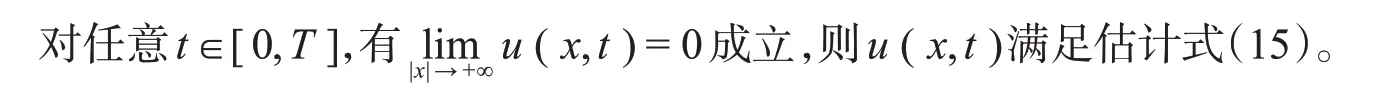
3 结束语

综上所述，本文利用一个基本的分析方法探讨了一类热传导方程以及一类具有一般形式的二阶线性抛物型方程初值问题解的最大模估计，其中不需要构造任何辅助函数以及利用初边值问题的极值原理，这不同于相关教材对这一问题的处理方法。本文的结果和方法都较为简单，有利于加强学生对热传导方程初值问题解的最大模估计的理解与掌握，从而丰富和改进了“偏微分方程”课程的教学，对于热传导方程初值问题的教学具有较好的参考价值。