量子计算时代的安全加密算法研究

王 东 李春平 张淑荣

（广东白云学院，广东 广州 510450）

1 引言

云安全是保护云计算数据和基础设施的一套机制。它用于保护用户的数据完整性、身份验证和机密性。云安全涉及数据存储和传输安全，其中，密码学是保障云计算安全的重要方法。量子计算基于量子物理原理，例如叠加和纠缠[1]，在量子计算中，仅仅增加几个额外的量子比特就可带来处理能力的指数级飞跃，将当前计算条件下需一万年的处理时间缩短为几分钟[2]。因此，量子计算机因其超高速的迭代加密密钥和破解密钥能力已成为云安全的主要威胁。本文对量子计算机对云安全以及当前的数据加密技术的影响进行展望，并提出针对量子计算机的安全加固方案。

2 传统加密算法

作为云安全的重要组成部分，密码学是一种大规模的分布式计算模型，在资源共享过程中保证信息的安全性和隐私性。目前使用的两种类型的密码系统是：对称密码体系和非对称密码体系。对称密钥算法(SKA)是单密钥加密，SKA使发送方和接收方拥有相同的密钥来加密和解密数据。目前常见的两种类型的SKA是：分组密码和流密码。分组密码使用密钥在电子数据块中对特定长度的比特流进行加密。系统将数据存储在其内存中，在加密过程中检索完整的块[3]。云计算中使用的主要的SKA加密方法包括DES、Triple-DES、AES和河豚算法。例如，Amazon Web Services (AWS)、Google AES 128）均为应用于数据存储的加密技术。非对称密钥算法(AKA)使用公钥加密发送给接收方的消息，使用私钥在接收端解密信息。接收者是其私钥的唯一持有者。在非对称加密系统中，每个接收者都拥有自己的解密密钥（私钥），接收方生成加密密钥（公钥）。通常，受信任的第三方参与确定特定公钥的所有者[4]。云计算中使用的一些流行的SKA技术包括：RSA、DSA、椭圆曲线技术等。

3 量子计算

量子计算是近几年来兴起的计算科学领域的研究热点之一。量子计算机中的量子位可以处于叠加状态，这意味着量子同时保持“开”或“关”状态，由于量子位于这两种状态之间的某个光谱上，而不仅仅是“开”或“关”两种状态。量子比特可以纠缠在一起。同时，两个粒子可以连接在一起，即使它们在物理上是分开的。量子计算机的行为方式与普通计算机完全不同，量子计算机的量子力学算法研究成为一门新学科。

3.1 易受量子算法影响的加密系统

密码学是目前确保电子邮件、密码或金融交易安全的主要认证识别手段，量子计算具有快速运算的能力，其已成为当前密码学的严重威胁。许多研究人员透露，量子计算机能够通过计算或尝试所有密钥方式，快速破解密码密钥。此外，黑客亦会利用持续优化的量子算法破解当前通信的安全加密算法。例如：Peter Shor的算法帮助量子机器找到整数的质因数；Lov Grover的算法帮助量子计算机迭代可能的排列。

3.1.1 Shor算法

Shor算法是Peter Shor于1994年发明的。2001年，IBM使用具有Shor算法的七量子位量子计算机将15分解为3和5，实现了量子计算机破解现有加密方法的初步尝试。非对称密码学使用素数分解作为其安全性的基础。素数分解是一项艰巨的任务，在普通计算机中仅靠穷尽计算很难在短期内实现破解。由于Shor算法可以快速解决素整数分解或离散对数问题[5]，配备了Shor算法的量子计算机可以破解现代非对称加密系统。

3.1.2 Lov Grover算法

1996年，Lov Grover发明了一种基于量子技术的数据库搜索算法，并在传统电脑中搭建了快速搜索引擎。对称加密算法的设计模式和密钥长度是衡量加密系统安全性的重要指标，如：AES系统，密钥长度为18的AES算法目前被普遍采用。借助量子计算机，Lov Grover算法能加速处理并将128位密钥转换为64位密钥的量子计算等效项并实现对AES加密系统的快速破解。在这种情况下，量子计算用于搜索未排序的数据库。搜索未排序的数据库需要线性搜索，这需要O(N)时间，但Lov Grover算法仅需一半的搜索时间便可在含有N个条目的乱序数据库中检索出某一特定条目。Lov Grover算法将对称密码的复杂度从O(N)降低到O(N/2)，这使得当前对称密码学的加密机制很容易被破解。

4 量子算法破解加密

4.1 Shor算法和非对称加密(RSA)

Shor算法可用于破解非对称密码系统。例如，RSA加密系统通常使用一对密钥：一个公钥和一个私钥。公钥用于加密消息，只能使用私钥解密。私钥是两个大素数p和q。这些数字相乘得到RSA算法的公钥N。将私钥相乘以计算公钥是一项轻松的任务，但几乎不可能将公钥分解为私钥。Shor的算法使分解变得更容易。它以一个随机数g开头。欧几里得算法用于寻找g和N的最大公约数，其中N是公钥。当g是N的一个因子或与N共享一个因子的情况下：找到N的最大公约数是一个素因子，比如q，然后找到另一个因子将是N除以q的简单数学问题。但在g和N互质的情况下，可猜测一个随机数g。随机数g具有N因子的概率可以通过以下数学事实来增加：如果两个数字a和b互质，则gp=m*b+ 1 ，可表示为：

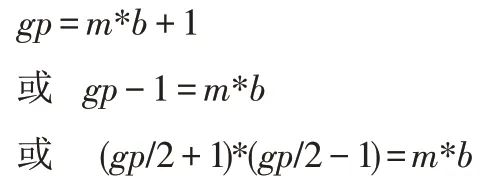
这时gp/2 + 1与N共享一个因子，并且最大公约数(gp/2 + 1,N)将给出N的素因子。但要计算最大公约数(gp/2 + 1,N) ，需要找到周期p。am(modb)表示两个相对素数，其中m = 0，1，2……依此类推[6]，给出了一个周期性的余数序列。这可以使用下面的数字2a(mod 15)看出：

2amod 15 20mod 15 21mod 15 22mod 15 23mod 15 24mod 15 Output 1 2 4 8 1

在这里，余数在间隔4之后重复。因此，周期是4。而针对复杂情况，特别是那些516位或以上的数字运算，采用传统的计算机很难在有效时间内得到解。但借助量子计算的手段，计算速度得到飞速提升。Shor的量子计算算法可以将随机的、很难被猜测到的g转换为gp/2 + 1 ，其与N共享一个因子的概率很高，其中p是重复周期。对于那些516位或更多的数字，量子计算机可以通过叠加输入的方法在短短几分钟内完成运算。首先取输入条件：1＞+2＞+3＞+...并通过输入条件提高初始数的幂并给出输出：g1＞+g2＞+g3＞+...，这是初始化数字对输入数字的幂。这些叠加被传递到另一台量子计算机中。第二台量子计算机计算gx(modN)并给出具有g的幂的余数叠加的输出结果，并用gx(modN)得出该余数，其运算过程如下：

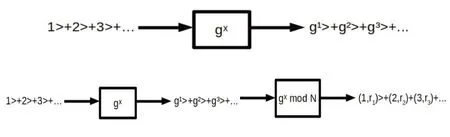
针对上面给出的g=2和N=15的例子，第二台量子计算机得出的输出结果是：

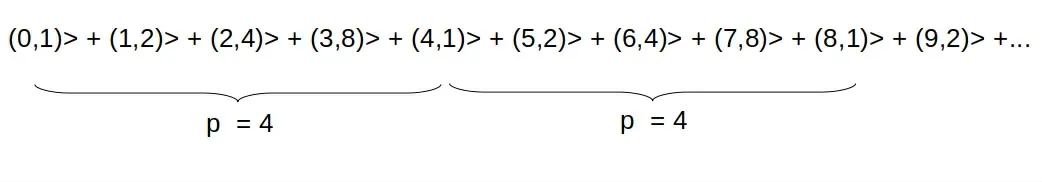
此时，计算结果在周期4之后出现重复。类似地，对于较大的数字N和g，其运算结果会在周期p之后出现重复。如果采用所有可能的幂的叠加来测量余数，那么量子计算机会给出可能的余数r的一种结果作为输出。虽然没有得到最终的解，但量子计算机中的状态叠加减少到仅产生余数r的g的幂，这个幂结果以p为周期重复，并将余数保留在叠加中。这种叠加可以被视为具有周期p和频率f的波。叠加的频率可以使用量子傅里叶变换计算（QFT）给出单个量子态作为输出( 1/p)。在p值已知的情况下，可以将猜测从g提高到gp/2 + 1 ，再次取(gp/2 + 1,N)的最大公约数，得出N的质因数之一，再通过将N除以p，得出另一个素因子[7]。此时，采用Shor算法的量子计算机就实现了对非对称加密算法的破解。

4.2 Lov Grover对称密码算法

配备Grover算法的量子计算机可迅速破解对称密钥算法(AES)。基于Grover算法的量子搜索算法可以在O(n1)中搜索关键空间，其包含一个二次加速。例如，对于n位对称密码算法，量子计算机重在破解2n个可能的方式。研究表明，量子计算机采用Grover算法后，针对AES128位加密系统，攻击时间可减少到264次，而对于AES-256位对称加密系统，攻击时间则减少到2128次。Grover算法的目的不仅是搜索密钥数据库，而且是将其描述为反相函数。假设我们有一个函数y=f(x) ，Grover的算法计算已知y的x的解。此时，求解反函数相当于在数据库中搜索出给定值y的x解，采用Grover算法的量子计算机在破解AES加密系统时极大地缩短了时间。

5 量子计算时代的密码学

量子计算机凭借其快速的计算机能力，结合相应的算法，已对现有基于传统密码学的云安全产生了威胁，但当前部署应用量子计算机的综合成本很高，目前虽然已有在云端部署量子计算服务的实例，但距离量子计算的广泛商用化还相距甚远[8]。由于早期的量子计算服务可能会通过云部署，因此云安全最迫切需要创建一个抗量子的安全系统。这种安全系统需要利用量子计算所具有的运算优势，将云安全的水平提升到更高的高度。新兴的量子密码学学说提出了构建量子计算分发量子密钥的密码系统，并被看作是量子计算时代的安全解决方案。

5.1 量子密码学

量子密码系统使用光子携带量子密钥，光子充当无法复制或更改的移动粒子。量子密码学的安全性依赖于光子的这一特性，使其在当前技术条件下不可攻破。量子密码学最重要的部分是量子密钥分发（QKD）。量子密钥分发是使用经过身份验证的通信通道来建立密钥的过程，使用一系列光子通过光缆将数据从发送方传输到接收方[9]。目前，很有希望取得成功的量子密钥分发的系统是BB84协议。在BB84协议中，量子位用于编码信息，光子用于携带该信息。

量子密钥分发对窃听具有很强的鲁棒性，考虑到光子状态在被复制或篡改时会发生变化，发送方可以检测到这种变化并向接收方发送新密钥以重新加密发送信息。量子密钥分发还可以创建一个具有量子弹性的安全和通信生态系统，因此即使使用量子计算机也很难破解基于量子的密码系统[10]。

5.2 量子计算的局限性

传统计算机需要数年才能完成的计算工作量对于量子计算机而言仅需要很短的时间，但量子计算机因其自身的计算特性存在着一些不稳定性和局限性影响了量子计算机的大规模应用[11]：

(1)基于量子的密码学需要在发送者和接收者之间建立一个量子通道，在当前的通信网络中还没有这种量子通道。

(2)量子计算机对噪声失真和环境影响极其敏感，对运算结果影响很大。

(3)量子计算在当前还处于运算论证和演示阶段，量子计算自身的脱散问题造成信息难以被存储。

(4)量子计算尚缺乏容错、纠错等机制，本身造成的错误率难以预测和发现。

6 量子计算时代密码学发展方向

尽管量子计算机以目前的能力可能无法破解当今所有的密码系统，但量子计算正在快速发展，新型的匹配算法正不断被推出。Shor和Grover的算法已被证实对当前密码系统造成了显著的威胁。量子计算机在计算时间和应对复杂任务方面的能力要远远优于传统的超级计算机。但目前适配量子计算机的算法还不多，例如：多重解决方案的问题还不能被量子计算机有效解决[12]。当前，主要有四种量子密码系统的研发引领着量子计算的发展方向。

6.1 基于格的密码学

基于格的密码学具有抵抗数百万量子位的容错通用量子计算机的密码破解能力。与RSA不同，基于格的加密方案不是乘以素数，而是采用乘法矩阵。最短向量问题(SVP)是一个NP-hard问题，其目标是在格中找到最小的非零向量。基于格的密码系统的安全性依赖于难以解决的格系统内的坐标[11]。目前，用于求解最短向量问题需要在多种方案中求最优解，而量子计算机无法通过多种解决方案快速解决问题。

6.2 基于多变量的密码学

基于多变量的密码学是一种采用公钥密码的加密系统，它使用有限域上的多变量方程系统作为其公共映射。其安全性取决于有限域上的二次多项式方程的NP硬度。多元加密方案目前是简单的矩阵加密方案，解密过程仅由线性系统的解组成。多元密码系统也可用于数字签名，UOV和Rainbow方案是代表例子。

6.3 基于哈希的密码学

基于哈希的密码学是一种量子认证密码方案，其广泛用于验证文档的数字签名中。LamportDiffie或Winternitz等数字签名与基于签名的RSA不同，基于散列的密码学产生的签名仅供一次性使用，它不受Shor算法等量子攻击的影响，即使使用量子计算机，要破解加密哈希函数也很困难。在后量子时代，基于散列的密码学因其对抗量子算法的鲁棒性而被寄予厚望。基于散列的加密已成为现有RSA和ECDSA的合理替代方案，在不久的将来基于散列的加密很可能会被广泛采用。

6.4 基于代码的密码学

基于代码的密码算法采用纠错码进行加密和解密。发送方和接收方通过嘈杂的信道进行通信。发送方通过噪声信道向接收方发送编码消息，接收方在另一端使用纠错码对消息进行解码。将来，随着基于代码的密码学的广泛使用，解码过程将耗时更久。基于代码的密码系统的典型代表例子是McEliece密码系统[13]，因其复杂性较低，它可以用于量子计算的加密密钥交换，也可实现快速加密和解密数据。

7 结论

量子计算时代终将到来，它将与计算机网络通信和人工智能等既有学科一起对世界产生深远影响。当前，以非对称算法和对称算法为代表的传统密码学在量子计算面前暴露出了安全的脆弱性。量子计算具有高效破解传统加密算法的技术条件。在量子计算方面，有研究显示出结合了Shor算法和Grover算法的量子计算机具有快速破解AES和DES等云计算常用的对称加密系统的能力[14]。本文对相关的科研成果进行了梳理，重点介绍了Shor和Lov Grover算法。以量子密码学为代表的量子安全伴随着量子计算的发展而发展，随着量子加密的实现，量子密码学将带来深远的技术革命，并将密码学的发展提升到一个新的高度。