基于可变模糊云的既有玻璃墙安全预警

张翔， 李芊， 王腊银， 黄歆

(西安建筑科技大学管理学院， 西安 710055)

玻璃幕墙作为一种质轻美观的建筑材料已广泛地应用于高层建筑的外围结构当中。目前，中国的玻璃幕墙产量与保有量已位居世界首位，并仍在不断攀升。玻璃幕墙的大范围使用虽然加快了建筑材料的转型，但随着老化现象的发生也带来了极大的安全隐患。根据《中国消防安全年报》的统计，2006—2018年全国发生既有玻璃幕墙安全事故高达2.9万起，造成人员伤亡达到0.8万人，经济损失约为1.3亿元[1]。因此，针对既有玻璃幕墙的安全管理研究具有重要的现实意义。

为实现既有玻璃幕墙的安全管理，最先开展的是基于安全风险因素的研究，例如，Goh等[2]在分析了大量既有玻璃幕墙实际工程的基础上，认为只需要掌握既有玻璃幕墙的不安全因素就能获悉它的安全等级，并就此提出了基于安全风险因素的既有玻璃幕墙综合评价法；李芊等[3]从全寿命周期的角度总结了玻璃幕墙的安全风险因素，认为提高既有玻璃幕墙安全性的关键在于首要风险因素的控制。尽管基于安全风险因素的研究对减少事故的发生具有一定的作用，但由于安全风险因素的获取较为复杂并且具有较强的主观性，仅仅依靠此类方法进行安全管理已无法满足实际的需要。于是，基于数理模型的既有玻璃幕墙安全评价研究便逐渐出现，例如，Efstathiades等[4]通过机器学习的方法，提出了基于人工神经网络(artificial neural network，ANN)的既有玻璃幕墙健康状态检测法，实现了幕墙体系缺陷的识别；金巾等[5]以突变理论与模糊数学为基础，提出了既有玻璃幕墙可靠性的评价方法；吴红华等[6]以差异与联系度系数为基础，提出了基于集对分析法的既有玻璃幕墙安全状态评价模型。此外，为分析既有玻璃幕墙的安全性，相关学者还主张通过仪器监测来实现，例如，王永祥等[7]针对结构胶的老化与失效问题，认为可以使用使用光栅传感技术对既有玻璃幕墙的安全状态进行鉴定；周易非等[8]针对玻璃幕墙受风形变问题，认为可以使用数字图像技术对既有玻璃幕墙的安全状态进行鉴定；Huang等[9]针对既有玻璃幕墙震动问题，认为可以使用激光测振仪(laser doppler vibrometer，LDV)对既有玻璃幕墙安全状态进行鉴定。基于上述分析，现有的安全管理研究大多是针对既有玻璃幕墙的可靠性检测与评价[10]，对既有玻璃幕墙的安全预警研究却相对较少，因此，根据“安全第一，预防为主”的基本思想，对既有玻璃幕墙安全预警的研究具有重要的理论价值。

云模型是一种专门研究复合不确定性问题的现代数学理论，可以较好地描述变量的不确定性，实现定性与定量之间的映射与转化[11]。目前，该方法已广泛地应用于围岩安全预警[12]、生态安全预警[13]以及自然灾害预防[14]等领域中并取得了较好的效果，该方法的提出也为实现既有玻璃幕墙安全预警提供了一定的借鉴。现以云模型与熵权理论为基础对主客观权重进行了组合，引入可变模糊集理论完成了数据的量化，提出相似度测算模型对警情状态进行诊断，并考虑模糊熵的大小对预警结果再判断，提出基于信息云组合权重、可变模糊云以及模糊熵的既有玻璃幕墙安全预警方法。

1 研究方法

1.1 云模型概述

云模型是以模糊理论为基础建立的概念转化模型[15]。

定义1假设X为一个特定的论域，在这个论域集中，∀x都有着特定的隶属度μ(x)，且隶属度μ(x)的大小均属于[0,1]，即

μ：X→[0,1],∀x∈X,x→μ(x)

(1)

当满足上述关系，便可以将x在论域上的分布定义为云，此时∀x都称为该云的云滴。

定义2任意云的形态，都可以通过3个数字特征来描述。假设C为某一正态云，则它可以表示为

C=(Ex,En,He)

(2)

式中：Ex为云的期望，它是描述特定主体的最佳隶属关系；En为云的熵，它是描述评价结果的可信程度，也是决定云滴扩散范围的关键；He为云的超熵，它是描述特定主体的稳定性，是决定云层厚度的关键。

定义3云发生器是实现定性概念与定量数据相互转换的特定算法[16]，它是由正向云发生器与逆向云发生器所组成，其工作原理如图1所示。

图1 正、逆向云发生器工作原理Fig.1 Working principle of forward and reverse cloud generator

1.2 信息云组合权重的确定

在进行既有玻璃幕墙安全预警的过程中，通常需要确定权重的大小。权重的确定方法主要包括主观赋权法与客观赋权法。运用主观赋权法，能够通过专家经验反映预警指标的重要性，而运用客观赋权法，能够有效反映指标间的数值关系，二者各有优点。此外，无论通过主观赋权抑或客观赋权，所赋予的权重也相差较大，即指标权重的大小是一个不确定值[16]。因此，为兼顾主客观权重的优点，考虑权重的不确定性，提出了信息云组合权重法。

通常组合权重是采用加法或乘法合成的方式，但上述两种组合形式的合理性相对较弱，组合后的权重是否兼顾了主客观权重的优点较难解释[17]。与上述方法不同，信息云组合权重法的基本思想是将赋予的权重认为是围绕真实权重的一组云滴，进而通过逆向云反应器进行权重云的生成，最后考虑权重云中熵的变化，通过熵权法的思想对权重进行修正。

假设在既有玻璃幕墙安全预警过程中，通过c种赋权方法对预警指标进行赋权，其中主、客观赋权法的数量分别为c1与c2，且满足c1+c2=c，则权重矩阵为

(3)

接着，根据逆向云发生器，便可以获得预警指标权重云的数字特征，其大小满足：

(4)

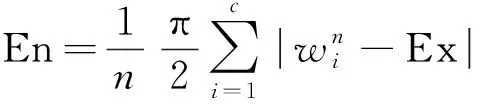
(5)

(6)

式中：S2为各项权重的方差，其大小满足：

(7)

(8)

为避免各方法所得到的权重值相距过大而产生赋权结果的误差，根据熵权法的计算规则，对各项指标的权重进行修正，此时组合权重的大小满足：

(9)

式(9)中：wj为各项预警指标的组合权重。

1.3 指标的量化

1.3.1 基于可变模糊集的定量指标量化

在传统云模型的计算中，通常是将检测所获得的样本直接作为云滴输入反应器中，从而获得所需要的数字特征。这种简单的转化过程在拥有大量样本的情境下是合理的，但考虑到既有玻璃幕墙的实际检测过程，所掌握的定量数据通常较少，其中部分还存在极端值的问题，若直接将实测数值导入云反应器中是不合适的。因此，通过可变模糊集理论对定量指标的量化过程进行改进。可变模糊集的优势在于能够动态地根据不同区间调整隶属关系，克服因数据过少或极端数据的出现而导致的误差情况[18]。

假设既有玻璃幕墙存在n个定量预警指标，每个指标又存在k个预警等级，则各指标的预警等级的区间可以用矩阵P来表示

(10)

式(10)中：cih和dih分别为第i个指标对应的第h个评价等级的上界和下界；i=1,2,…,n；h=1,2,…,k。

设Mih为第i个指标在第h个评价等级区间内，相对差异度为1的点，则Mih的大小满足:

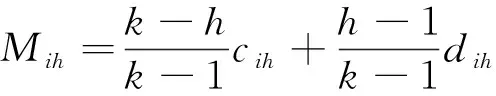
(11)

此时,定义X0=[cih,dih]为指标i的吸引域，X=[ci(h-1),di(h+1)]为包含X0的某一区间[18]，它们的关系如图2所示。

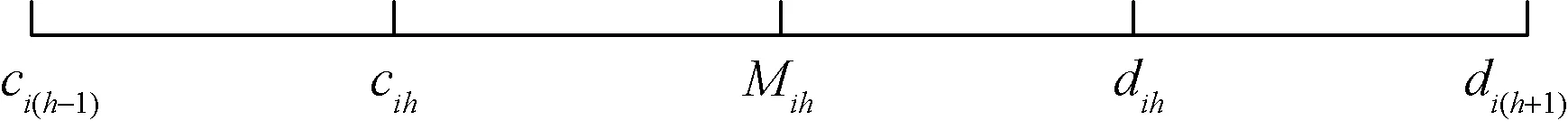
图2 上、下界限与吸引域的关系图
Fig.2 The relationship between the upper and lower limits and the attraction domain

x

ij

x

ij

M

ih

D

ih

x

ij

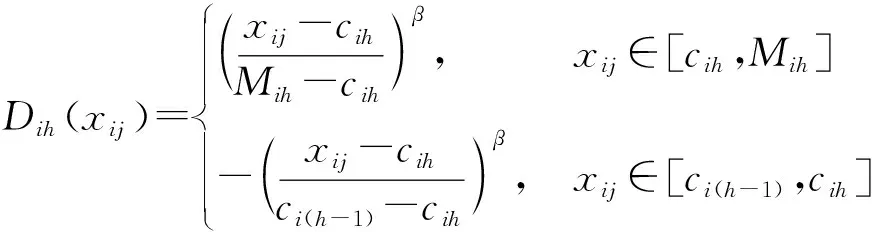
(12)

式(12)中：β为非负指数，该指数的大小通常取1。

当实测值xij>Mih时，则指标对于吸引域的相对差异度Dih(xij)为

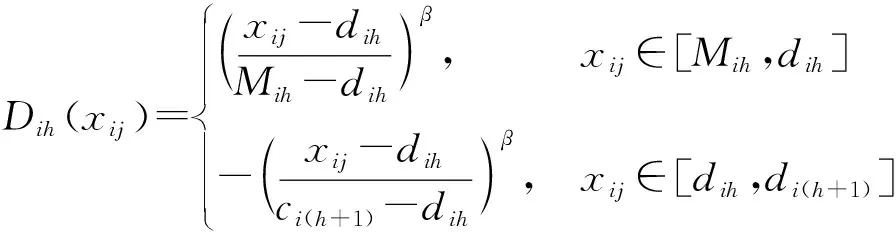
(13)

定义μih(xij)为隶属度，其大小满足：

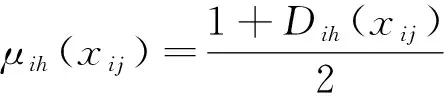
(14)

在得到各样本对预警等级的隶属度后，进而计算各等级的平均隶属度μih，并将其作为加权值[19]，代入逆向云发生器中，便可以生成各定量指标的可变模糊预警云：

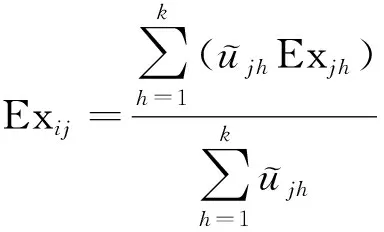
(15)

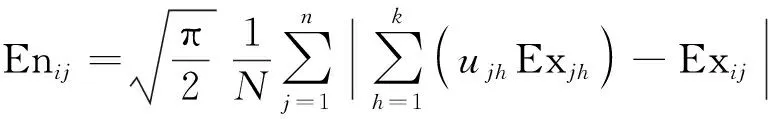
(16)

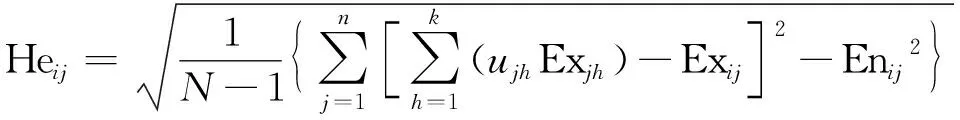
(17)

式中：Exij、Enij、Heij分别为可变模糊云的期望、熵、超熵；m为各预警单元中实测样本的数量；Exjh表示第j个指标对应第h个评价等级的期望。

1.3.2 基于三角模糊数的定性指标量化

在安全预警的过程中，相较于其他主体结构，在既有玻璃幕墙的指标体系中存在着较多的定性指标，如何量化定性指标对既有玻璃幕墙的安全预警也起着重要的作用。鉴于此，通过三角模糊数的引入，对定性语言进行转化，具体如下。

假设存在n个预警单元，m个检测位置，其对应的评语集为Q，评语集中存在着l个评价等级，则评语集Q可以表示为

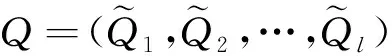
(18)

(19)

式(19)中：q1、q2、q3为评语的3个模糊数；f∈{0,1,2,…,l}。

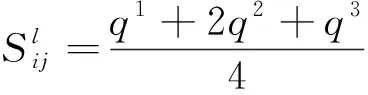
(20)

式(20)中：Sij为量化后的定性指标值。

1.4 模糊熵的确定

在预警的过程中，熵可以用来衡量预警结果的模糊性，一般将其称为模糊熵[20]。由于既有玻璃幕墙的安全预警通常是一个多层次、多因素的复杂性问题，其过程包含着大量的不确定信息，这就导致警情的确定过程常常出现难以避免的随机性与模糊性，因此通过单一算法对预警等级的判定难以真实的反映特定主体的安全现状，可以考虑在一维预警的基础上引入模糊熵作为警情大小的参考量。

假设模糊熵为E，则它的大小[20]满足：

(21)

式(21)中：m为模糊参数，其大小满足：

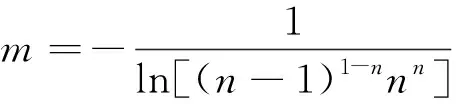
(22)

式(22)中：n为预警等级的数量；μi为既有玻璃幕墙预警结果对于第i级的隶属度大小；i=1,2,…。

模糊熵的大小对应着不同的复杂程度，其对应关系如表1所示。

表1 模糊熵的划分Table 1 Division of fuzzy entropy

由表1可知，当模糊熵的计算结果属于[0.0,0.1]与(0.9,1.0]以及(0.1,0.20]与(0.8,0.90]时，说明既有玻璃幕墙一维预警结果的状态为清晰或较清晰，此时各项安全预警指标对等级的归属差别较小，既有玻璃幕墙的安全预警结果复杂程度较低；反之，当模糊熵的计算结果属于(0.2,0.80]时,说明既有玻璃幕墙一维预警结果模糊，此时各项安全预警指标等级的归属差别较大，既有玻璃幕墙的安全预警结果复杂程度较高。

1.4 既有玻璃幕墙安全预警流程

步骤1基于预警要求，建立预警指标体系，明确定性指标的模糊语言与定量指标的等级区间。

步骤2通过信息云组合权重法，获得预警层与预警单元的组合权重。

步骤3确定既有玻璃幕墙的预警区间，并生成各预警等级的正态云，计算过程满足：

(23)

式(23)中：Exh、Enh和Heh分别为各预警等级的期望、熵和超熵；Bmax、Bmin为各预警区间的最大和最小值；k为常数，取0.001。

步骤4量化预警指标，结合权重大小，引入虚拟云模型[16]，生成预警层及幕墙整体的综合云。

步骤5求解综合云与各级评语云之间的相似度，计算如下。

假设综合云为Ci、评语云为Cj，定义θ为相对距离，则Exi的大小满足：

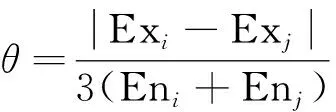
(24)

式(24)中：Exi、Eni、Hei分别为综合云Ci的数字特征；Exj、Enj、Hej为评语云Cj的数字特征。

根据向量间的余弦关系与相对距离，便可以获得两者之间的相似度计算公式：

Sim(Ci,Cj)=(1-θ)cos(Ci,Cj)

(25)

(26)

式中：Sim(Ci,Cj)为预警云与评语云的相似度。

步骤6计算模糊熵的大小，根据表1确定复杂程度，此时二维预警结果WP可以表示为

WP=(L,E)

(27)

式(27)中：L为通过虚拟云得到的一维预警结果。

2 实例分析

为验证上述预警方法的有效性与科学性，以某附属医院的既有玻璃幕墙为例进行分析。

2.1 案例背景

某附属医院的建筑主体高度为124 m，根据设计文件的记载，该建筑外围的幕墙类型为隐框玻璃幕墙。该建筑的幕墙结构自竣工验收后并未进行定期的安全性检测。

2.2 既有玻璃幕墙安全预警体系的建立

既有玻璃幕墙安全预警体系的构建是一个循序渐进的过程，预警体系的构建流程如图3所示。

对于既有玻璃幕墙的风险因素，目前尚未有统一的标准。在确定既有玻璃的风险因素时，是基于《民用建筑可靠性鉴定标准》以及《玻璃幕墙工程质量检验标准》等相关标准，并配合专家调查法的方式所确定。对于既有玻璃幕墙安全风险类型的识别，是以既有玻璃幕墙的主要结构为划分依据，将二者相匹配，便可以初步得到既有玻璃幕墙的安全评价指标的建立依据，如表2所示。

图3 既有玻璃幕墙安全预警体系的建立步骤Fig.3 Steps to establish a safety evaluation system for existing glass curtain wall

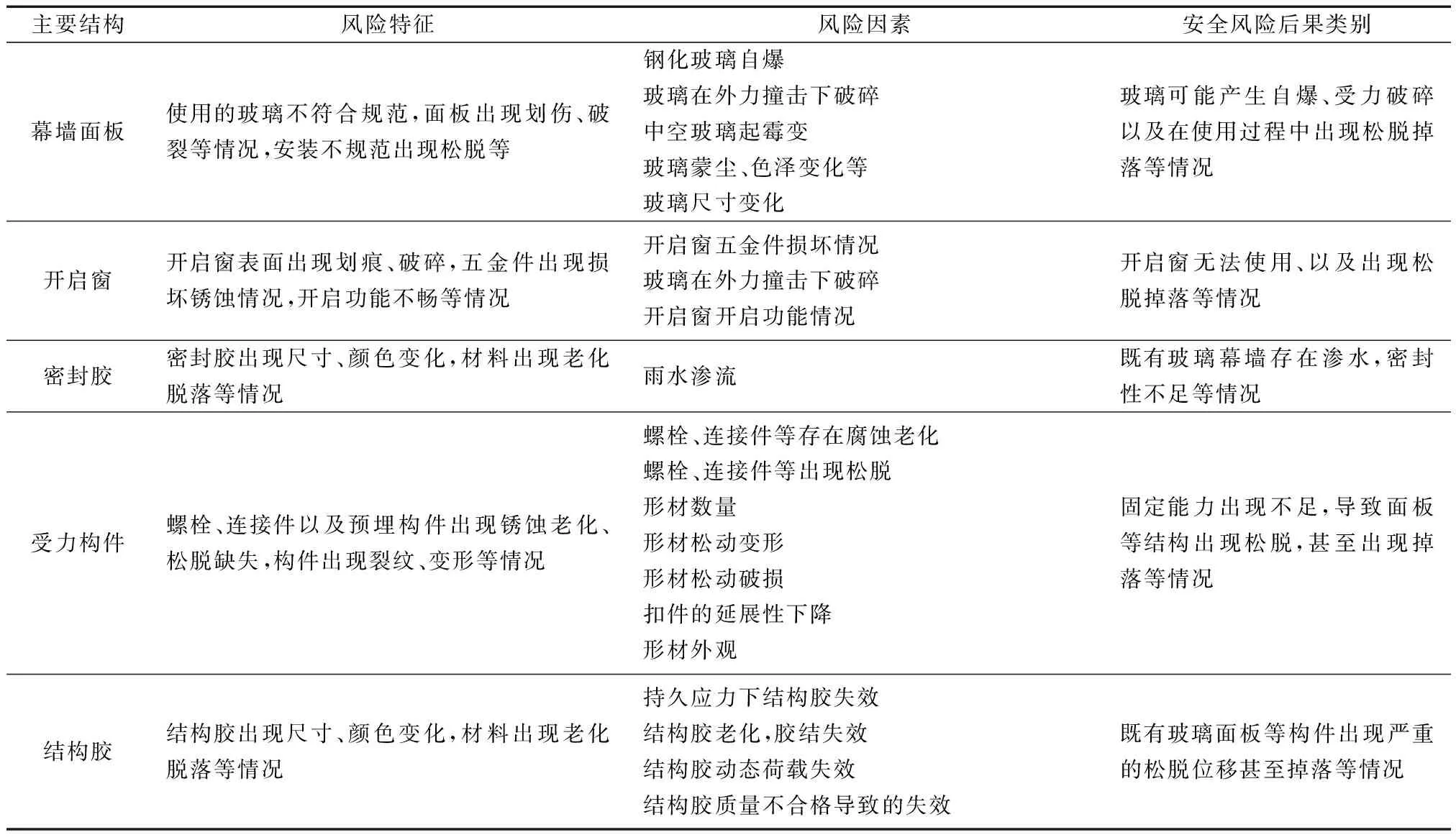
表2 既有玻璃幕墙安全风险类型Table 2 Types of safety risks for existing glass curtain walls

于是，根据表2便可以初步明确既有玻璃幕墙预警层与评价结果的初步范围，再结合实际检测的相关经验，便可以构建通常条件下的既有玻璃幕墙安全预警体系，如图4所示。

2.3 既有玻璃幕墙安全预警等级的确定

确定评语云的目的是为了与综合云形成对照，从而推断警情的大小。假设J为警情集合，将既有玻璃幕墙的警情划分为5个等级，则J满足：J=(JAu,JBu,JCu,JDu,JEu)。假设预警值的范围属于[0,1]，对上述5个等级进行赋值并就相应的预警等级提出安全处理对策，结果如表3所示。

2.4 指标的赋值

2.4.1 定量指标的赋值

划分定量指标的等级区间，根据可变模糊集原理[式(10)～式(17)]，确定指标的平均隶属度，进而通过改进的逆向云发生器实现定量指标预警云的生成，计算结果如表4所示。

图4 既有玻璃幕墙安全预警体系Fig.4 Existing glass curtain wall safety evaluation system

表3 既有玻璃幕墙安全预警等级的划分与处理对策Table 3 Classification and treatment countermeasures of the existing glass curtain wall safety warning level

2.4.2 定性指标的赋值

基于专家对定性指标的评价，通过三角模糊数，实现定性语言的量化，计算结果如表5所示。

2.5 组合权重的计算

分别采用层次分析法、熵权法等多种主客观赋权方式，确定既有玻璃幕墙的预警单元与预警层的单一权重，再通过式(3)～式(9)进行组合，便可以获得各指标的组合权重，计算结果如表6所示。

2.6 预警结果

基于表4～表6的计算结果，通过虚拟云算法便可以生成各预警层及幕墙整体的综合云，如图5所示，继而通过式(24)～式(26)确定综合云与评语间的相似度，计算如表7所示。

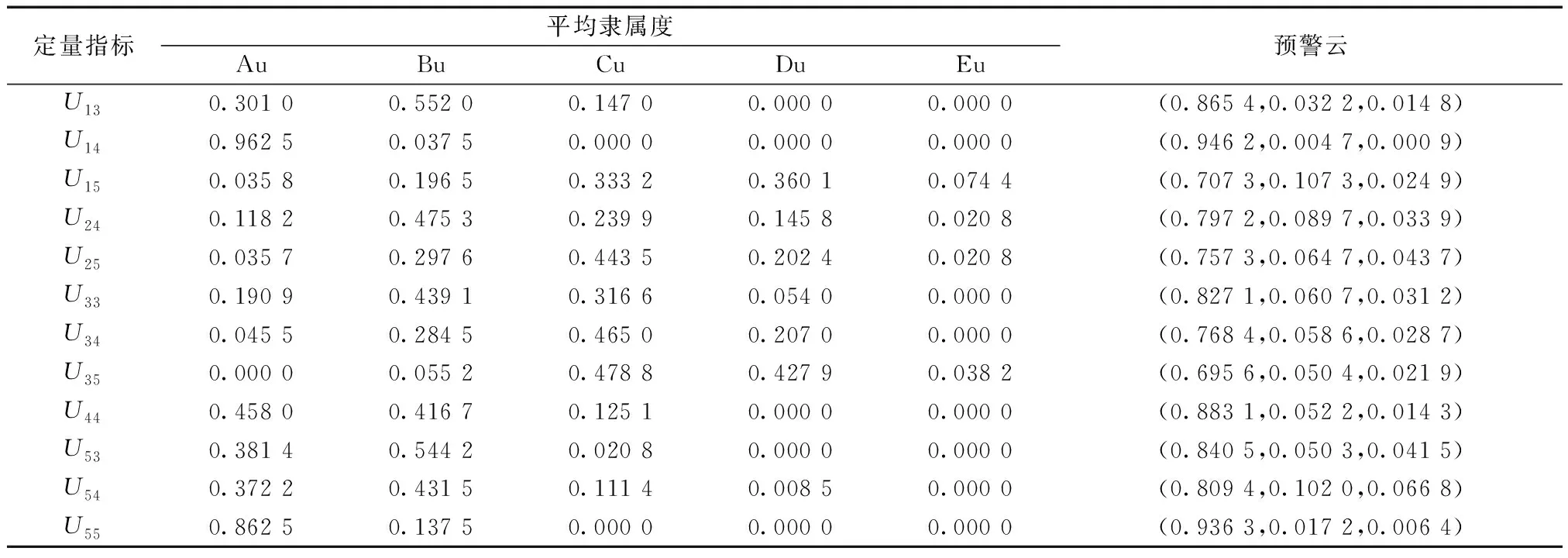
表4 各定量指标的平均隶属度及预警云计算Table 4 Average membership degree of each quantitative index and warning cloud computing

表5 定性指标预警云Table 5 Qualitative indicators of the warning cloud

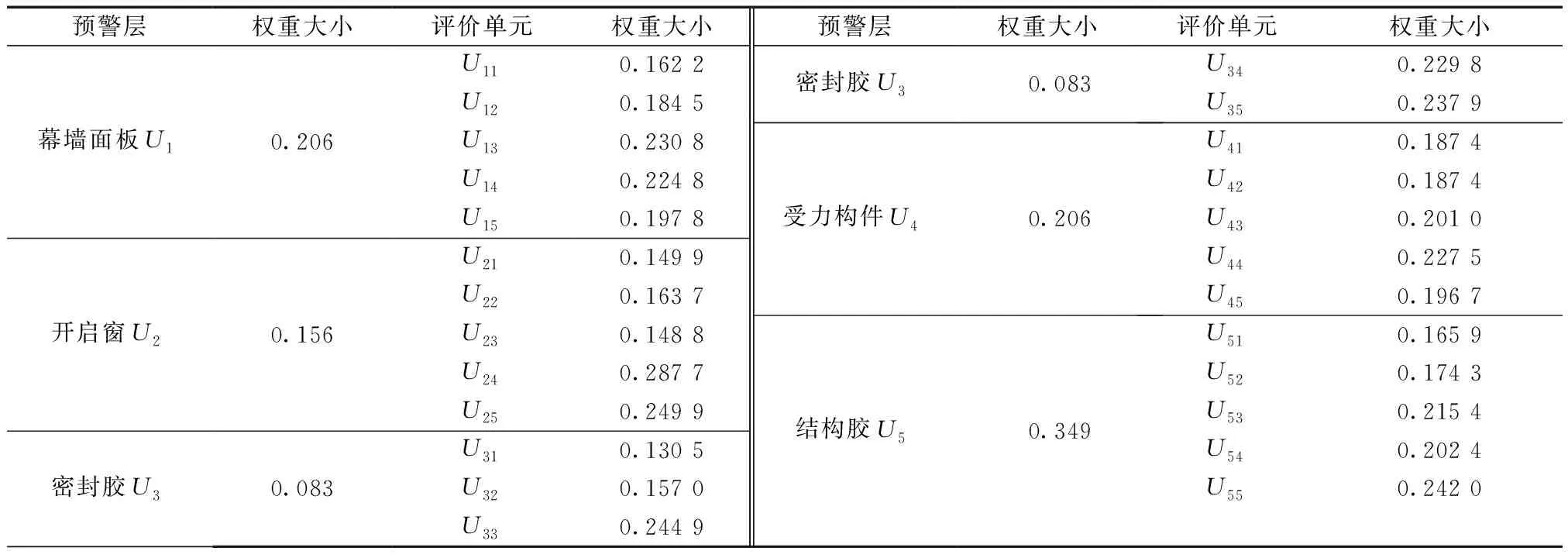
表6 预警层与评价单元的组合权重Table 6 Combination weights of evaluation layers and evaluation units

表7 诊断云及其相似度计算Table 7 Diagnostic cloud and its similarity calculation

以既有玻璃幕墙面板的一维预警分析为例，根据表7与图5所示的结果，既有玻璃幕墙面板的预警云对各预警等级的相似度大小为：Sim(Au)=0.414 2，Sim(Bu)=0.776 0，Sim(Cu)=0.855 0，Sim(Du)=0.493 3，Sim(Eu)=0.067 1，显然存在Sim(Cu)>Sim(Bu)>Sim(Du)>Sim(Au)>Sim(Eu)的大小关系，因此该既有玻璃幕墙的警情大小应为“中警”，所采取的安全处理对策应为：针对问题部位进行修补、加固和更换，并进行二次抽查。同理，其余构件的预警等级及安全处理措施如表8所示。

2.7 模糊熵与二维预警结果

为进行既有玻璃幕墙的二维预警，基于表7的相似度结果，代入式(21)～式(22)便可以获得模糊熵，继而根据式(27)便可以确定既有玻璃幕墙的二维预警结果，具体结果如表9所示。

3 讨论

3.1 敏感性分析

为了更加有效地对既有玻璃幕墙的警情进行掌握，除了进行上述的分析，还应该进一步掌握既有玻璃幕墙预警层中各评价单元的敏感性，实现更为深入的安全控制。本文以U11～U55为输入变量，进行4 000次演化，则各预警层中各指标的敏感性大小如图6所示。

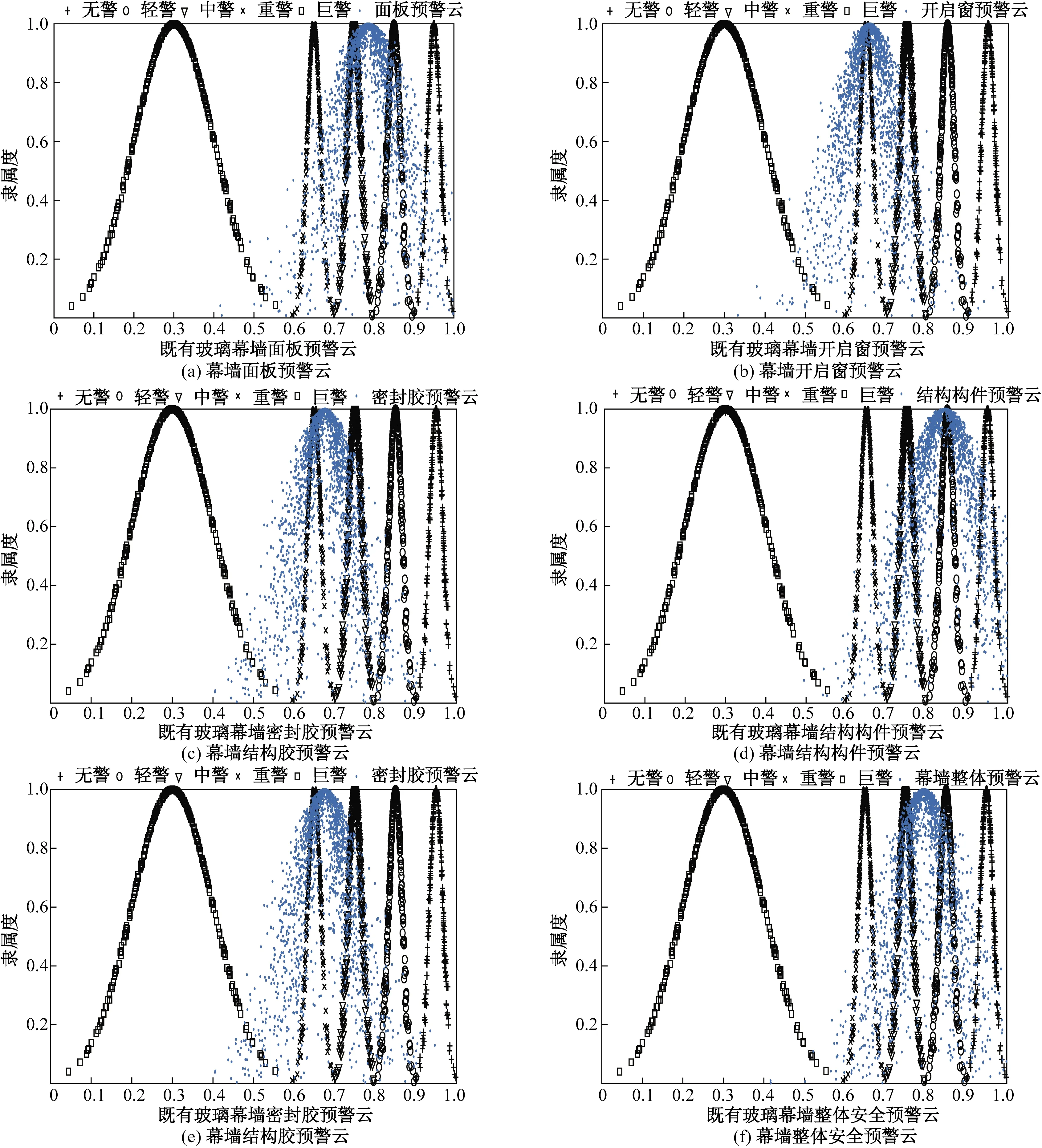
图5 既有玻璃幕墙的综合预警云Fig.5 Existing glass curtain wall comprehensive warning cloud

表8 既有玻璃幕墙的警情大小及安全处理措施Table 8 The size of the alarm and safety measures for the existing glass curtain wall

表9 既有玻璃幕墙的二维评价结果与安全处理措施Table 9 Two-dimensional evaluation results and safety treatment measures of existing glass curtain wall

图6 各预警层中评价单元的敏感性大小Fig.6 Sensitivity of evaluation units in each evaluation layer

根据图6可知，对于各预警层的安全性而言，敏感性指标也不尽相同。针对既有玻璃幕墙面板，其对面板承载力状况最为敏感；针对既有玻璃幕墙开启窗而言，其对开启窗表面的承载力状况最为敏感；针对既有玻璃幕墙密封胶，其对密封胶的邵氏硬度最为敏感；针对既有玻璃幕墙受力构件，其对受力构件的承载力最为敏感；针对既有玻璃幕墙结构胶，其对密封胶的断裂延伸率最为敏感。因此，在日常的维护过程中，警情控制的重心不仅要放在预警结果所反映出的薄弱环节上，还应该同时加强对各预警层中的敏感性指标的安全监控，从而有效地完成警情的控制。

3.2 方法比较

进一步检验本文方法的有效性，将分级法、模糊综合评判法与其比较，结果如表10 所示。

根据表10的对比结果，3种方法所得到的结果在幕墙面板、开启窗、受力构件、密封胶以及整体的预警上并无分歧，主要存在分歧的是结构胶的预警

表10 既有玻璃幕墙预警等级对比分析表Table 10 Comparative analysis table of warning levels of existing glass curtain walls

等级，但结合工程实际的鉴定结果以及现场对结构胶的描述与实测结果，最终认为其预警等级为轻警是科学合理的。此外，与其他两种方法相比，方法3的优势如下。

(1) 在针对既有玻璃幕墙进行一维预警的基础上，考虑模糊熵，分析了预警结果的复杂性，确定了既有玻璃幕墙一维预警结果模糊熵的大小为0.866 6。根据表1的模糊熵划分结果，确定了该结果属于“较清晰”范围，即表明各项预警指标归属度较好，既有玻璃幕墙的预警结果复杂程度较小，不需要采取进一步的安全处理措施，预警要求可以相对放宽。模糊熵的计算，在一维预警的基础上，将其转变为包含预警等级与复杂性大小的二维预警结果。

(2) 模糊综合评判法虽然在数理的角度对既有玻璃幕墙进行了有效的预警，但在预警的过程中却忽略了指标及其权重的不确定、随机性与模糊性，通过引入虚拟云模型，便可以有效克服上述弊端，从而得到更为准确的预警结果并实现既有玻璃幕墙警情状态的可视化。

(3) 基于可变模糊集的思想，构建了定量指标的可变模糊预警云有效克服了因预警指标过少或者极端数值出现而引起的误差，从而更能适应实际工程的要求。

4 结论

基于上述模型建立与实例的计算，可以得到如下结论。

(1)基于既有玻璃幕墙安全风险因素的识别，考虑既有玻璃幕墙在安全预警过程中的不确定性，通过虚拟云模型的引入，实现了既有玻璃幕墙的一维预警。此外，为了进一步评估警情变化的可能，引入模糊熵辅以判断，实现了既有玻璃幕墙的二维预警。该方法在一维预警的基础上，既能有效的克服预警过程中的不足，实现既有玻璃幕墙安全预警的可视化，还严格考虑了预警结果的复杂程度，从而有效地为后期维护提供了参考。

(2)基于可变模糊集理论，改进了逆向云发生器，提出了可变模糊云算法，实现了预警云的生成，有效地克服了因预警指标过少或者极端数值的出现而引起的误差。此外，由于指标权重的不确定性，综合考虑主观与客观权重的特点，基于正态云与熵权法的思想进行了权重的组合，使权重大小更满足工程实际的需要。

(3)将该方法的预警结果与其他模型进行对比，得出该方法的预警结果是科学且合理的，并且通过预警层的敏感性分析可知相应评价单元的敏感性贡献值，从而有针对性地对敏感性指标进行安全控制。

(4)该方法的研究意义在于不仅实现了既有玻璃幕墙的安全预警，降低了幕墙安全事故发生的可能，还能为实际工程的维护提供一定的参考。但不可否认的是，该方法仍然存在一定的不足，例如主客观赋权方法数量、预警体系优化等问题，这些不足需要在后续的研究中进一步讨论。