三空间分割遗传算法的环氧乙烷灭菌装载问题

2022-06-14张美洲周敏黄静文陈燕军

科学技术与工程 2022年14期

张美洲，周敏，黄静文，陈燕军

(1.武汉科技大学冶金装备及其控制教育部重点实验室, 武汉 430081； 2.武汉科技大学精密制造研究院, 武汉 430081； 3.武汉科技大学机械传动与制造工程湖北省重点实验室, 武汉 430081)

环氧乙烷(ethylene oxide, EO)灭菌作为医疗器械(口罩、纱布片、手术衣等)终末灭菌的主要选择，是保证产品达到无菌条件[1]的关键工序。随着新型冠状病毒肺炎疫情的爆发，无菌医疗器械的供应一度严重短缺，EO灭菌再度引起了中外众多学者的关注。何乐春等[2]和Weiss 等[3]用实验的方法对灭菌参数进行了优化研究，提出可以通过缩短灭菌周期来提高企业的灭菌产能，但是存在灭菌参数验证周期时间较长的缺点。虽然辐照灭菌被认为是一种高效的灭菌方式[4]，但是众多研究表明辐照灭菌不适用于医疗口罩产品的灭菌生产[5-6]。作为一种绿色的灭菌方式，超临界二氧化碳灭菌技术目前还处于实验室阶段，暂没有工业生产的案例[7-8]。

工业EO灭菌需要在防泄漏、防爆炸的密闭钢制灭菌柜[9]中进行，以便能对产品进行批量灭菌，从而提高灭菌效率，降低单次灭菌成本，因此提高灭菌柜的容积利用率是消除灭菌工序瓶颈的主要方法之一。待灭菌产品装载到灭菌柜的过程，就是一个三维装箱的多项式复杂非确定性完全问题(non-deterministic polynomial hard，NP-hard)。自从Johnson[10]在20世纪60年代率先提出一种近优的装箱算法后，该领域已从一维装箱问题发展到了三维装箱问题的研究。尚正阳等[11]提出了一种概率较优空间分割和底面积匹配放置规则的快速求解三维装箱问题的优化算法。于明正等[12]和张钧等[13]都使用了空间分割和遗传算法相结合的方式，来解决三维装箱问题。由于装箱问题有着众多的实际应用背景，Erbayrak 等[14]考虑了平衡性和产品族对于三维装箱的影响；张长勇等[15]和Paquay 等[16]分别用改进遗传算法和两阶段启发式算法对航空领域的装箱问题进行了研究；Saraiva等[17]采用分层算法研究了三维装箱问题在汽车公司的应用。

综上所述，目前对于产品EO灭菌效率提升主要集中在参数优化和方法替代上，对于灭菌装载问题的研究中外均没有相关文献。基于此，现采用三空间分割的遗传算法来解决产品EO灭菌装载效率低的问题。为保证有交期要求的产品能够优先进行装载，引入三段式基因编码。同时运用惩罚函数弛批次约束，消除了不符合批次要求的装载组合对结果的影响。双精英保留策略也可以确保有交期要求的产品占比和灭菌柜容积利用率两种装载组合形式都可以得到最优值，以便于对实际生产进行指导。与实际生产中的经验装载方案对比，本算法的装载方案在装载时间和灭菌柜容积利用率上都有很大的提升。

1 EO灭菌装载问题的数学模型

1.1 问题描述及约束条件

EO灭菌装载问题定义为：给定一个容积长、宽、高为L、W、H的灭菌柜和i种长宽高为li、wi、hi数量为Mi的产品，在考虑产品交期要求和批次要求约束的同时，确定合理的产品EO灭菌装载方案，最大化地利用灭菌柜的容积。

生产订单都有交期的要求，希望有延期风险的产品能够尽量多的优先生产。因医疗器械需要满足追溯的要求[18]，故根据产品类别和投放市场的不同，特定产品需要在同一批次生产。本文研究主要考虑如下两种实际约束：①交期要求约束，即有交期要求的产品优先安排灭菌；②批次要求约束，即有批次要求的产品需要同时进行灭菌，或者都不在灭菌组合中。

1.2 模型假设

结合EO灭菌生产实际情况并参照文献[11-13]，EO灭菌装载问题需要做如下假设：①灭菌柜内部形状为长方体；②灭菌柜内产品的放置位置没有区域限制；③待装载产品均为长方体且质量分布均匀；④产品没有放置方向约束，可以随意转动，且没有码放层数限制；⑤产品底部完全支撑，不能出现悬空；⑥有批次要求的产品总量占比在20%以内，主要为整批生产后的尾单产品。

1.3 模型建立

基于以上分析，现将EO灭菌装载问题的数学模型建立如下。

(1)目标函数为灭菌柜容积利用率最大：

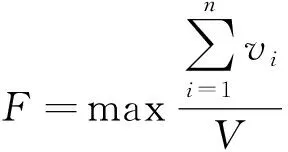
(1)

式(1)中：F为灭菌柜容积利用率；待灭菌产品序号i=1,2,…,n；vi为第i件产品的体积；V为灭菌柜的容积。

(2)产品总体积约束：

(2)

(3)产品装载三维尺寸约束：

(3)

式(3)中：xi、yi、zi为待灭菌产品i的三维空间坐标；li、wi、hi为长、宽、高；L、W、H为灭菌柜内部尺寸。

2 模型求解算法

遗传算法(genetic algorithm，GA)，又称为进化算法，因其具有良好的隐形并行性和全局搜索能力，而被广泛应用于求解NP-hard问题。三空间分割算法的核心思想是将产品按照规则放入选定的空间中，并对放入后的空间按照上、右、前的方式进行分割，形成3个新的独立子空间。本文模型求解算法由三个步骤组成：①通过遗传算法来形成待灭菌产品的初始装载方案，为后续的算法准备初始解集；②采用三空间分割算法对初始解集进行解码求值；③通过适应度函数找到最优的产品装载方案。三空间分割的遗传算法流程如图1所示，虚线框内为三空间分割算法。

图1 三空间分割的遗传算法流程图Fig.1 Flow chart of genetic algorithm with three-space segmentation

2.1 三段式基因编码

针对EO灭菌装载问题的交期约束，采用三段式基因编码方式，即编码由有交期要求产品装载顺序、没有交期要求产品装载顺序和产品放置方式三段组成，确保有交期要求产品优先装载。

(1)产品装载顺序编码。设总的产品数量为n，对产品按照有交期要求和没有交期要求进行排序，假设1～m为有交期要求的产品，m+1～n为没有交期要求的产品。采用自然数对产品进行编码，然后生成两段基因：G1={P1,P2,…,Pm}，G2={Pm+1,Pm+2,…,Pn}。

(2)产品放置方式编码。因本文研究中对产品的旋转方向没有要求，故每种产品都有6种摆放方式，编码值用自然数1～6表示。产品放置方式的基因编码可以表示为：G3={Pn+1,Pn+2,…,P2n}。

完整的三段式基因编码表示为：G={P1,P2,…,Pm,Pm+1,Pm+2,…,Pn,Pn+1,Pn+2,…,P2n}。

2.2 定序规则

定序规则是指将产品装入灭菌柜的先后顺序的规则，产品装载顺序对灭菌柜容积利用率有直接影响。为了降低特定的定序规则对布局质量的影响，采用遗传算法的三段式基因编码作为产品的定序规则，即由G1和G2基因段对应的编码顺序来确定产品放入的顺序。可以用如下伪代码来描述定序规则，如算法1所示。

算法1三空间分割的定序规则

G1+G2→N#由G1和G2的编码生成产品序列N

fori=1∶N#通过循环依次取得产品i

ifi≤N#如果序列中有产品

geti; #得到第i个产品

else

break;

end if

end for

2.3 子空间搜索规则

选定待装载的产品后，需要进行子空间的搜索，以确定是否有满足尺寸要求的子空间，来装载该选定的产品。当子空间的尺寸和产品的尺寸满足式(4)时，则此子空间可以作为该产品的装载空间。

(4)

式(4)中：xb、yb、zb为子空间的长、宽、高；li、wi、hi为产品i的长、宽、高。为了提高灭菌柜容积利用率，采用最小体积策略确定装载产品的子空间，即在所有的可装载子空间中，选取体积最小的子空间来装载选定的产品。其子空间搜索规则的伪代码如算法2所示。

算法2三空间分割的子空间搜索规则

SpaceList→M#子空间的列表为M

ascend by volume ofM#对子空间按照体积升序排列

forj=1∶M#通过循环依次取得子空间j

ifi≤j#判断产品i和空间j是否满足式(4)

getj; #如果满足式(4)，则选取对应的子空间

else

j+1; #如果不满足式(4)，则选取下一个空间

end if

end for

ifj=NULL #如果所有子空间都不满足式(4)

i+1; #跳转到算法1，选取下一个产品

else

break;

end if

2.4 定位规则

定位规则是指产品在空间中的放置方式，主要包含两个方面，一是产品的旋转方向，这个由三段式基因编码的G3基因段确定三维坐标和产品长(l)、宽(w)、高(h)的对应关系，即产品的旋转方向，产品放置方式解码表如表1所示；二是产品在选定的子空间中的放置位置，本文研究采用占角策略，即将产品放置在选定的子空间的左后下角。点(a,b,c)和(e,f,g)为空间的左后下角，产品定位规则如图2所示。

2.5 三空间分割规则

当灭菌柜中装入一个产品后，灭菌柜中的空间结构发生了变化，被占用空间除去产品所占用的体积外，剩余部分被分割为上、右、前三个新的子空间，并产生如图3(a)和图3(b)两种三空间分割规则，如图3所示。

表1 产品放置方式解码表

图2 产品定位规则图Fig.2 The map of product positioning rule

图3 三空间分割规则Fig.3 Three-space segmentation rule

三空间分割规则应该避免细小空间的产生，因为细小空间会降低后续产品放入的概率，从而降低灭菌柜容积利用率。原空间被分割完成后，需要从空间列表中删除，并剔除分割后的零体积子空间，最后将剩余新生成的子空间加入空间列表中。本文研究的三空间分割规则的伪代码如算法3所示。

算法3三空间分割规则

SelectedSpace→V0#选定的空间V0

#将空间V0按照图3(a)规则分割形成前(Vaf)、右(Var)、上(Vat)三个子空间

V0segment according to
Fig.3(a) →Vaf、Var、Vat

#将空间V0按照图3(b)规则分割形成前(Vbf)、右(Vbr)、上(Vbt)三个子空间

V0segment according to
Fig.3(b) →Vbf、Vbr、Vbt

ifVaf>Vbr

V0segment according to
Fig.3(b); #采用图3(b)规则分割

exclude {Vbf、Vbr、Vbt}=0; #剔除体积等于零的空间

#将剔除零体积后的子空间加入到空间列表SpaceList中

then add {Vbf、Vbr、Vbt} →SpaceList;

else

V0segment according to
Fig.3(a);#采用图3(a)规则分割

exclude {Vaf、Var、Vat}=0;

then add {Vaf、Var、Vat} → SpaceList;

end if

deleteV0; #删除原空间V0

update SpaceList; #更新空间列表

将一件长宽高为a、b、c的产品按照如图3(a)所示的方法装入灭菌柜后，其分割后新生成的三个子空间如下。

前空间Vf的空间编码f及尺寸为

(5)

右空间Vr的空间编码r及尺寸为

(6)

上空间Vt的空间编码t及尺寸为

(7)

2.6 子空间合并规则

将灭菌柜中的细小子空间合并为更大的子空间，不仅可以降低细小子空间不能容纳其他产品的情况，而且可以提高灭菌柜容积利用率和空间的搜索效率。其中图4是子空间的前后合并，图5是子空间的左右合并。子空间合并规则的伪代码如算法4所示。

算法4三空间分割的子空间合并规则

#用坐标和三维尺寸表示子空间Space1和Space2，其中(a,b,c)为子空间的坐标，(xb,yb,zb)为子空间的长宽高

Space1 {a1,b1,c1,xb1,yb1,zb1}, Space2 {a2,b2,c2,xb2,yb2,zb2}

if (a1>a2 anda1=a2+xb2) or (a1

merge according to
Fig.4 → Space3 {min(a1,a2),b1,c2,

xb1+xb2,yb1,zb1}; #按照图4合并为空间Space3

delete Space1 and Space2; #删除子空间Space1和Space2

#将合并后空间添加到空间列表，并更新列表

then add Space3 → SpaceList and update SpaceList;

else if (b1>b2 andb1=b2+yb2) or (b1

merge according to
Fig.5 → Space4 {a1,min(b1,b2),c1,xb1,yb1+yb2,zb1}; #按照图5合并为空间Space4

delete Space1 andSpace2;

then add Space4 → SpaceList and update SpaceList;

else

break；

end if

图4 子空间的前后合并Fig.4 Forward and backward merging of subspaces

图5 子空间的左右合并Fig.5 Left and right merging of subspaces

2.7 惩罚函数和适应度函数

在EO灭菌生产中，灭菌参数和EO气体的加入量是固定的[19]，故单次灭菌的产品总体积越大，则效率越高，经济效益越好。采用目标函数，即灭菌柜容积利用率作为适应度函数，故适应度越大，则子代的适应性越好。同时引入惩罚函数来松弛批次要求约束，当具有批次要求的产品没有同时进行灭菌生产时，则直接剔除对应的灭菌装载方案。

(1)惩罚函数。设产品的种类为k，Rk=1表示产品k具有批次要求约束，Rk=0表示产品k没有批次要求约束，SNk表示已经装载到灭菌柜中的第k种产品的数量，Mk为产品k的总数量。惩罚函数为

(8)

只有当产品k具有批次要求约束Rk=1，在灭菌柜中的装载数量SNk≠0，且装载数量SNk≠Mk时，惩罚函数α=0，其他情况下惩罚函数α=1。

(2)适应度函数。灭菌柜容积利用率越大，则适应度越大，子代基因的适应性越好。但对于不符合批次要求约束的子代基因，可以通过惩罚函数α=0，将适应度β设置为0，这样在后期遗传迭代中该基因会被淘汰。F为灭菌柜容积利用率。

β=αF

(9)

2.8 双精英保留和轮盘赌选择算子

选择算子是指挑选装载方案的策略，即根据适应度函数从父代装载方案中选择符合要求的装载方案。根据本文问题采用双精英保留策略，对灭菌柜容积利用率和有交期要求产品占比两个参数分别进行精英个体(elite)保留，作为下一代个体基因。然后删除精英个体，再执行多次轮盘赌补足基因种群要求的数量。

(1)个体方案被选中的概率为

(10)

式(10)中：Pi为个体i被选中的概率；N为筛选后剩余种群总数。

(2)个体方案被选中的累计概率为

(11)

式(11)中：Qi为个体i被选中的累计概率，即装载方案在[0-1]区间上分段，然后通过多次轮盘赌，选择相应的基因，淘汰未被选中的基因个体。

2.9 顺序交叉算子

遗传算法的基因交叉方式有很多，因顺序交叉不仅可以维持原基因段的部分结构，且可以产生较好的子代基因，故以此方式作为交叉算子。根据三段式基因编码，产品装载顺序在其各自基因段内进行顺序交叉，再根据装载顺序部分交叉点的位置，产品放置方式部分的编码值在其对应的位置上进行交换。

设编码字符串长度为2n，通过交叉概率函数判断基因交叉是否发生，若是，则分别以[1,m]和[m+1,n]为取值范围生成两对整数作为交叉点，再根据顺序交叉的方式，来交叉前两段的基因值；根据装载顺序部分交叉点位置，放置方式的基因值在与其对应的位置上进行交换。顺序交叉示意图如图6所示。

F-G1和F-G2表示父代基因；C-G1和 C-G2表示生成的两个子代基因图6 顺序交叉示意图Fig.6 The diagram of sequential crossover

2.10 变异算子

变异是保证装载方案多样化的关键过程之一。在本问题求解中，产品的放置方式是影响装载效率的重要因素之一，本文研究中的变异算子主要是对放置方式基因段的编码进行变异。根据产品摆放方向约束的限制，放置方式在相应的取值范围内进行随机变异，基因变异示意图如图7所示。

FG表示父代基因；CG表示变异后的子代基因图7 基因变异示意图Fig.7 The diagram of gene variation

3 实验案例与分析

针对实际约束的三维装载问题，现在没有统一的国际标准数据进行对比，约束的类型和产品种类的多少，都对装载效果有较大的影响。本文研究的EO灭菌装载问题采用MATLAB编程语言，算法代码在MATLAB R2015b上运行，计算机配置数据为：Intel©Core i7-1065G7 CPU 1.30 GHz，内存8 GB，操作系统为Windows 7专业版。

3.1 实验案例设计

综合本文讨论的实际约束，需要确定待灭菌产品是否有交期要求和批次要求，并将此参数作为算法的约束条件。其中，有交期要求的产品代码为Rd=1，没有的为Rd=0；有批次要求的产品代码为Rb=1，没有要求的为Rb=0。为了便于观察仿真的装载效果，采用红绿蓝(red green blue， RGB)色彩模式对不同产品进行颜色区分。待灭菌产品主要参数如表2所示。

遗传算法的初始参数设置为：迭代次数iteration=200，种群规模population=100，交叉概率cross=0.9，变异概率设置两个阶段，前100代variation=0.5，以便于增加子代的多样性，后100代variation=0.1，以便于加快结果的收敛，灭菌柜容积利用率和有交期要求的产品体积占比各保留精英个体比率elite=5%。灭菌柜采用优尼克公司生产的20 m3EO灭菌柜，其内部有效空间为：L×W×H=900 cm×125 cm×165 cm。

表2 待灭菌产品主要参数

3.2 实验结果与分析

由算法结果可知，全局最优解在迭代到第180代时，基本趋于稳定，遗传算法迭代图如图8所示。针对需要求解的灭菌柜容积利用率最大的问题，在交期要求和批次要求的约束下，其对应有4种灭菌装载方案，如图9产品装载图所示。并根据方案选择策略，确定在不同的约束条件下，最终的灭菌装载方案，灭菌装载方案及方案选择如表3所示。其中，A表示有交期要求的产品体积占比，即已装入灭菌柜的有交期要求产品体积之和与待灭菌产品中有交期要求产品的总体积的比值。B表示灭菌柜容积利用率，即已装载的产品总体积与灭菌柜容积的比值。

图8 遗传算法迭代图Fig.8 The iteration graph of genetic algorithm

表3 灭菌装载方案及方案选择

图9 产品装载图Fig.9 Product loading diagram

由表3可知，当Rb=1时，在Rd=1的情况下选择装载方案R1-1，在Rd=0的情况下选择装载方案R1-2；当Rb=0时，在Rd=1的情况下选择装载方案R1-1，在Rd=0的情况下选择装载方案R2-2。

为验证本文算法的有效性和优越性，调研了中国某医疗企业灭菌车间25次灭菌装载的平均时间和灭菌柜容积平均利用率，并与本次仿真结果进行对比，遗传算法和经验装载结果对比如表4所示。

表4 遗传算法和经验装载结果对比

由表4对比数据可知，采用三空间分割的遗传算法在装载时间和灭菌柜容积利用率上，都要优于现在的经验装载方案。经验装载不仅需要大量的时间进行合适产品的筛选和放置方法的反复调整，而且会因为装载方案不当而导致产品延期风险加大和批次管理失效等情况。采用三空间分割的遗传算法的装载方案，在给定的条件下，通过对灭菌柜容积利用率不断的迭代寻优，则可避免这些问题。并根据实际生产需求，结合不同的约束条件，选择对应的装载方案，相比经验装载灭菌柜容积利用率提高了12.1%～15.9%。