基于改进块贝叶斯学习的多通道心电信号重构

2022-06-14凌振宝单君娜董冉

科学技术与工程 2022年14期

凌振宝，单君娜，董冉

(吉林大学仪器科学与电气工程学院，长春 130000)

美国国立卫生研究院于2020年发布的报告显示，心血管疾病(cardiovascular diseases，CVD)总患病人数从1990年的2.71亿增长到2019年的5.23亿，CVD年死亡人数从1990年的1 210万增长到2019年的1 860万[1]。心电(electrocardiogram, ECG)的实时监测是实现CVD早期诊断、降低CVD死亡率的有效方式。可穿戴式ECG监测系统一直是近年来研究的热点，该方法不仅可以全天候持续监测使用者的ECG信号，而且可以将数据同步到云端供医生远程问诊[2]。

由于可穿戴式ECG监测设备受尺寸、成本和佩戴舒适度的影响，传感器节点的电池容量有限，面临着如何减少功耗的挑战[3]，传感器节点的电能消耗主要来自无线传输和数字信号处理[4]，压缩感知技术(compressed sensing, CS)可以应用于可穿戴设备对ECG信号的采样和重构过程，该方法能减少无线传输的数据量并降低传输中的能量消耗[5]。Candes等[6]最先利用凸优化方法从欠采样的数据中重构信号，此后，CS被广泛应用于图像处理[7]、特征提取[8]、生理信号重构[9]等方面。

CS已广泛应用于单通道ECG信号的采样与重构过程，Balestrieri等[10]提出了一种以确定性矩阵为观测矩阵，以墨西哥小波为稀疏基，以正交匹配追踪法(orthogonal matching pursuit, OMP)为重构算法的ECG信号压缩采样新方法。齐林等[11]对比选择了不同的稀疏基，以基追踪法(basic pursuit, BP)为重构算法对心电信号进行恢复。这些方法都是针对稀疏后的ECG信号提出，凸优化算法和贪婪迭代算法对于信号中接近于零的元素无法精确地恢复，而ECG信号中接近于零的元素是诊断疾病的重要部分。Liu等[12]提出了一种快速块稀疏贝叶斯学习(block spare bayesian learning, BSBL)算法来重构胎儿心电和脑电信号，该算法在速度和数据重建准确度之间具有良好的平衡。由于在多导联ECG信号中存在更多病理信息和临床成分[13]，心脏病专家更倾向于用多通道ECG信号进行诊断。Polania等[14]将跨尺度小波的相关性的先验信息结合到ECG信号的重构算法中，并利用连续ECG区间的小波表示结构提高重构质量，但只验证了该方法对MIT-BIH心律失常数据库中双通道ECG信号重构的有效性，并没有在其他多通道ECG数据库中进行验证。

基于此，现将BSBL与多测向量模型(multiple measurement vector model, MMV)结合，提出一种可同时重构多通道ECG信号的方法，并在实验中重构双通道ECG信号和8通道ECG信号，以期为多通道ECG信号重构提供理论基础。

1 方法

1.1 面向可穿戴ECG信号监测系统的CS

当原始信号或其某些变换域中具有稀疏表示，则可应用CS对信号进行压缩，然后通过求解优化问题进行信号的重构。图1展示了基于CS的可穿戴ECG信号监护系统的工作流程，如图1所示，首先，传感端通过模数转换器对ECG信号进行采样；然后，数字心电信号经过观测矩阵被压缩，并将压缩后的数据传输到远程终端；最后，在远程终端应用CS重构算法从观测点中重构ECG信号。

图1 基于CS的可穿戴ECG监护系统Fig.1 CS-based wearable ECG monitoring system

1.2 结合MMV的BSBL框架

由于许多生物信号具有丰富的时间相关性，根据BSBL模型，原始信号X具有这样块的结构：

(1)

式(1)中：di为列向量分块的数量，其中i=1，2，…,g，其值不一定相同，每个块中的条目具有相关性，可以利用这种相关性提高信号重构的性能[15]。

结合MMV的CS基本框架可以表示为

Y=ΦX

(2)

式(2)中：Y为经过观测的信号；Φ为观测矩阵；X={x1,x2，…,xP}为采集到的多通道ECG信号，xi∈RN×1为第i个通道的信号。图2描述了X这个整体的数据包以及结合MMV的心电信号块，其中，第i个块由xi构成。

图2 MMV算法与BSBL结合Fig.2 Combination of MMV and BSBL

在BSBL模型中，X满足多元高斯分布：

p(Xi;γi)=MN(Xi;0,γiIdi,Ip)

(3)

式(3)中：γi为决定Xi稀疏性的方差参数；Idi、Ip为正定矩阵，用于描述块内元素之间的相关结构。γi的学习过程决定了第i块的相关性。式(3)可以写为

p(X;{γi})=MN(Xi;0,Γ,Ip)

(4)

式(4)中：Γ为块对角矩阵，其对角线上的元素与γiIdi对角线上的元素保持一致。

建模测量值Y为

p(Y|X;β)=MN(Y|ΦX;β-1IM,Ip)

(5)

式(5)中：IM为正定矩阵；假设噪声向量满足多元高斯分布，β为噪声的精度参数；MN 为矩阵的高斯分布。

由式(4)和式(5)可得

p(X|Y;{γi},β)=MN(X;μ,Σ,Ip)

(6)

式(6)中：

μ=βΣΦTY

(7)

Σ=(Γ-1+βΦTΦ)-1

(8)

使用第二类最大似然估计可以估计出BSBL框架中的参数，其损失函数为

L({γi},β)≜-2lgp(Y;{γi},β)=NlgC+

Tr[YTC-1Y]

(9)

式(9)中：C=β-1IM+ΦΓΦT。

使用快速边缘似然最大化方法优化损失函数，用Φi∈RM×di表示Φ的第i块，式(9)中的C被写为

(10)

(11)

=L(-i)+L(i)

(12)

通过优化L(i)更新γi：

(13)

使用快速边缘似然最大化算法，该算法在重构性能几乎不变的前提下，可使BSBL的运算速度加快至原来的8倍左右。计算过程从近似零解空间开始迭代求解，在计算完代价函数后，依次重新计算μ、Σ、{si}、{qi}，当代价函数的最大变化小于设定阈值η时迭代停止，η设置为1×10-5。

2 实验所用数据库及评价指标

2.1 数据库

使用MIT-BIH心律失常数据库(MIT-BIH arrhythmia database, Mitdb)、MIT-BIH噪声测试数据库(MIT-BIH noise stress test database, Nstdb)[16]和联邦物理技术(physikalisch-technische bundesanstalt， PTB)诊断数据库，Mitdb中包含48组双通道ECG信号，每组ECG信号的长度为30 min，采样频率为360 Hz，数模转换的增益为200 units/mV，ADC转换的分辨率为11位，ADC的零值为1 024。Nstdb中包含了12条长度为30 min的含噪声ECG信号以及3个长度为30 min的噪声信号，噪声信号分别为基线漂移、肌电干扰、电极运动噪声。其中，12个含噪声的ECG信号是由Mitdb中的记录118和记录119添加经过校准的噪声而成，每条信号的前5 min未添加噪声，此后每隔2 min添加一次噪声。PTB诊断数据库包含来自290名受试者的549条ECG记录，每条ECG记录包括15个通道的信号，分别是12个常规导联(I、II、III、aVR、aVL、aVF、V1、V2、V3、V4、V5、V6)，3个弗兰克导联(Vx、Vy、Vz)，采样频率为1 000 Hz，数模转换的增益为2 000 units/mV，ADC转换的分辨率为16位。在医学诊断中，多通道ECG信号通常以12导联的格式记录，在这12个通道中，有8个独立通道：I、II、V1、V2、V3、V4、V5、V6，而剩下的4个是衍生通道； III、aVR、aVL、aVF[17]。本文研究中使用多通道ECG信号中的8个独立通道。

2.2 评价指标及实验平台配置

使用均方根失真百分比(percentage root-mean-square distortion, PRD)和联合PRD(Joint PRD)来衡量心电信号的重构精度，PRD和Joint PRD的计算公式为

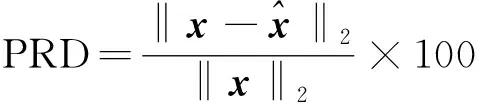
(14)

(15)

PRD值越小，表示信号重构的精度越高，PRD小于9%时，表示重构的信号可以用于医学诊断[18]。

使用每1 024个点的重构时间来衡量心电信号重构的速度，使用的计算机具有3.60 GHz的 CPU和4.00 G的RAM。

3 实验及结果分析

3.1 实验设置

Mitdb中双通道ECG信号以每个通道1 024个点为单位被分割，长度为30 min的信号被分割为632段，由于数据量过多，在每632段信号中随机抽取10段进行实验；选取PTB诊断数据库中ECG信号每个通道前1 024个点进行实验。使用本文改进的BSBL算法对分割后的每段心电信号进行重构时，按64个点长进行均匀分块。

压缩率(compression ratio, CR)定义为

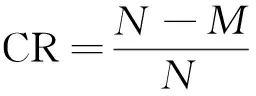
(16)

式(16)中：N为原始ECG信号的采样点数；M为数字ECG信号经过观测矩阵Φ压缩后的观测点数。

将参考文献[19]中的确定性二进制块对角矩阵改进后作为观测矩阵，参考文献[18]中构造的观测矩阵为

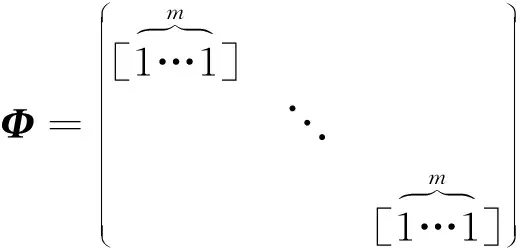
(17)

式(17)中：m=N/M，由相同的块构成该矩阵的对角线，每个块包含m个元素。

为使压缩率分别为10%、20%、30%、40%、50%、60%、70%和80%，在N=1 024的条件下，本文实验需要构造M=921、M=819、M=716、M=614、M=512、M=403、M=307、M=204的观测矩阵，所以没有固定式(17)中m的值，而是组合的方式使Φ的维数为M×N。

3.2 实验结果

3.2.1 相同压缩率下的ECG信号重构效果比较

为直观地表现出本文提出重构算法的有效性，图3给出了在固定压缩率为50%的条件下，Mitdb中不含噪声的ECG记录100在5种算法下重构信号的时域图，这5种算法分别是OMP、BP、加权迭代最小二乘(iteratively reweighted least squares，irls)、BSBL和本文改进的BSBL重构算法，为清晰地对比不同算法的重构效果，图3只给出了通道1的ECG信号波形。经计算，在压缩率为50%时，使用OMP算法重构ECG信号的PRD为8.34，使用BP算法重构ECG信号的PRD为16.99，使用irls算法重构ECG信号的PRD为20.97，使用BSBL算法重构ECG信号的PRD为8.77，使用本文改进的BSBL算法重构ECG信号的PRD为6.89。因此，压缩率为50%的条件下，对于ECG记录100，BP、SP算法的重构结果无法应用于医学诊断，BSBL算法重构的心电信号虽然可以应用于医学诊断，但其PRD高于本文算法的PRD，所以本文改进的BSBL重构算法对ECG信号的恢复效果更好。

图3 心电信号记录100原始波形与5种算法下的重构波形Fig.3 The original waveform of ECG recording 100 and the reconstruction waveform under 5 algorithm

为测试本文重构算法对含噪声ECG信号的重构效果，对Nstdb中的ECG信号进行了测试，计算了在固定压缩率为50%的条件下，不含噪声记录118和含噪声记录118e24、118e18、118e12、118e06在5种算法下重构ECG信号的PRD。

如表1所示，随着ECG信号信噪比的降低，重构的PRD逐渐增大，本文算法对记录118及其不同信噪比下ECG信号的重构PRD均仍小于9%，因此验证了本文改进的BSBL重构算法对含噪声ECG信号重构的有效性。

同时计算了PTB诊断数据库中所有数据的平均重构PRD，为了表示本文方法对不同疾病的表现差异，对PTB诊断数据库的5个主要病理类型分别进行了评估。如表2所示，在固定压缩率为70%的条件下，不同病理类型多通道ECG信号的平均重构PRD虽然有差异，但每个类型和每个通道的重构PRD均小于9%。

3.2.2 不同压缩率下的ECG信号重构效果比较

为验证改进的BSBL算法在重构精度方面的优势，将改进的BSBL算法与OMP、BP、irls、BSBL重构ECG信号的PRD进行对比。图4给出了不同压缩比下，对于Mitdb中的ECG信号，本文改进的BSBL重构算法与OMP、BP、irls、BSBL重构ECG信号时PRD的变化趋势，如图4所示，虽然在CR比较小的条件下，本文方法重构ECG信号的PRD高于OMP、BP、irls这三种算法，但是随着CR的的增大，本文方法重构ECG信号的PRD缓慢增加，而OMP、BP、irls这三种算法重构ECG信号的PRD增长速度很快；在所有CR的条件下，经本文改进的BSBL算法重构ECG信号的PRD均低于BSBL算法。经计算，本文方法的平均重构精度比BSBL算法平均重构精度提高了35.02%，证明了本文改进的BSBL重构算法的有效性。

表1 不含噪声记录与含噪声记录心电信号在5种算法下的重构PRD

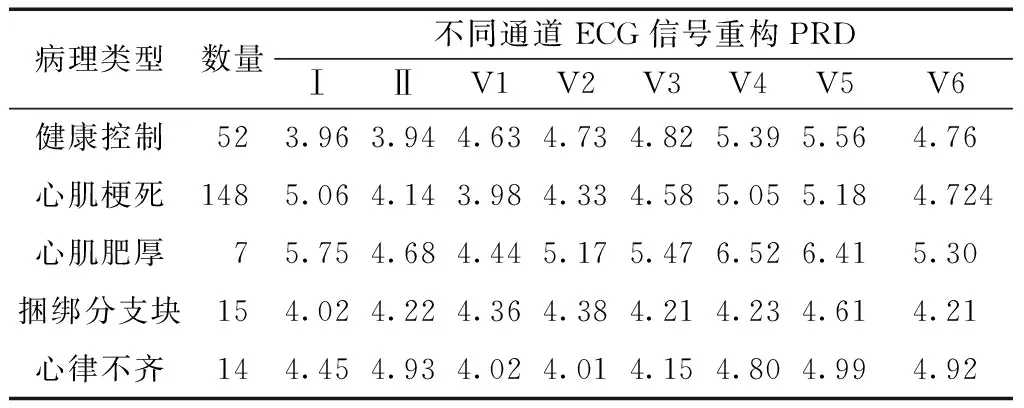
表2 不同病理类型多通道ECG信号的重构PRD

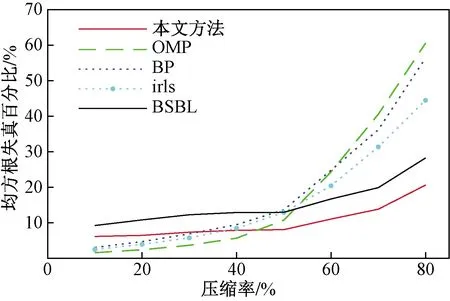
图4 不同压缩率下的5种算法重构PRDFig.4 Reconstruction PRD of 5 algorithms at different compression ratios

为验证本文算法在重构速度方面的优势，将改进的BSBL算法与OMP、BP、irls、BSBL重构ECG信号的平均重构时间进行对比。表3给出了不同压缩比下，对于Mitdb中的ECG信号，5种算法的平均重构时间，如表3所示，在同一压缩率下，本文改进的BSBL算法的重构时间虽然比BP算法的重构时间长，但是在多数情况下比OMP和irls算法的重构时间短；经计算，本文方法的平均重构速度是BSBL算法平均重构速度的8.08倍。结果表明，本文方法在速度和性能之间取得了良好的平衡。

为显示不同压缩比下，改进的BSBL算法对多通道ECG信号的重构效果，计算了PTB诊断数据库中ECG信号的联合PRD。如图5所示，随着压缩率的增加，联合PRD也随之增大，但都小于9%。本文直接对多通道ECG信号进行重构，原始ECG信号中包含基线漂移、肌电干扰、工频干扰等噪声，图5表明本文改进的BSBL算法在处理含噪声多通道ECG信号时表现良好。