基于Tent映射NSGA-Ⅱ算法的微电网多目标优化方法

2022-06-14王艳张嘉琳赵洪山

科学技术与工程 2022年14期

王艳，张嘉琳，赵洪山

(华北电力大学电气与电子工程学院，保定 071003)

为应对全球气候变化推动低碳经济发展，中国在第七十五届联合国大会上提出了“碳中和目标”。随着这一愿景的提出，清洁高效的能源体系备受关注。分布式发电具有较高的能源利用率和供应可靠性[1]，因此越来越多的分布式发电作为一种新的发电形式被广泛使用。微电网技术是一种把新型能源进行网络化处理的技术，有利于能量的传输和管理。为了达到分布式电源高效利用与电能质量互补的目的将微电网与配电网(power distribution network，PDN)互联，与之相关的能量管理系统也逐渐成为现如今研究的热点问题[2-3]。因此对并网条件下的微电网进行能量优化管理具有重要意义。

目前，中外对微电网能量优化管理的研究主要为在给定的目标函数和约束条件下确定各发电单元的实时出力情况，相关的研究已取得了一些成果。其中部分文献的研究视角主要侧重于微电网运行的经济性。文献[4]中以最小运行成本为目标函数分别对直流微电网和交流微电网系统进行讨论。文献[5]中以风力发电机和储能电池(storage battery，SB)为研究对象，以运行利润最大化为目标函数。但上述文献研究的目标函数较为单一只考虑其运行的经济性，缺乏实际应用的能力。而在实际运行中的微电网除了考虑其运行经济性，还需考虑对环境的影响和能源的损耗，故其能量管理模型应为多目标函数下的优化模型，在文献[6]中将微电网的经济性、污染物排放量与机组异步度作为目标函数。文献[7]中选取的目标函数为微电网运行的经济成本、二氧化碳排放量和循环电量。但上述文献仅考虑了微电网运行的成本，没有将微电网运行成本和运行收益相结合，对微电网运行的经济性考虑不全面。随着容量配置优化模型的建立，对优化问题的求解算法显得格外重要，其中除了将多目标函数加权变为单目标函数外[8]，还可采用智能算法进行求解。文献[9]采用SARAP算法求解单机微电网多目标容量优化配置问题。文献[10]采用粒子群算法，提出一种含储能装置和可调负荷的需求侧能量优化管理方法。文献[11]采用改进人工蜂群算法，实现独立交直流混合微网的电源优化配置。但上述文献提出的智能算法易使最终解集陷入局部最优。

针对上述问题，现提出一种双层能量优化管理方法，上层为模糊管理系统确定微电网运行模式，下层为多目标优化层确定微电网能量优化管理策略。该策略首先在约束条件下，以微电网运行经济性最大化、网络中碳排放量和有功功率损耗最小化为目标函数，建立容量配置优化模型。其中将微电网运行经济性最大化目标函数建模为微电网运行成本-运行收益最小化目标函数。其次采用基于Tent混沌映射改进NSGA-Ⅱ算法对多目标函数进行优化求解。最后运用算例验证文中所提能量管理方法、容量配置模型以及改进NSGA-Ⅱ算法的优越性。以期为微电网各机组供电配置以及能源配置方案的求解提供理论基础。

1 双层能量优化管理模型

并网运行条件下的微电网包含：火力发电机(thermal generator，TG)以微型燃气轮机(microgas turbine，MT)和燃料电池(fuel cell，FC)为主要发电单元；可再生能源(renewable energy sources，RES)以风力发电机(wind turbines，WT)和光伏发电单元(photo voltaic，PV)为主。文中所提出的能量管理系统(energy management system，EMS)模型是双层能量优化管理模型：上层为模糊管理系统，下层为多目标函数优化层。该双层能量优化管理模型如图1所示。

图1 双层能量优化管理模型Fig.1 Two-layer energy optimization management model

上层模糊管理系统通过得到的光伏出力PPV和风力发电机出力PWT、每小时住宅负荷需求PL来确定混合微电网的工作模式。并将上述得到的数据和确定的工作模式通过通信通道传递给下层对能量进行优化管理。

在模糊管理系统中将微电网的工作模式划分为4种，不同模式下各分布式电源的运行情况如下。

模式一：当混合微网中的负荷很小时，可再生能源发电即可满足负荷需求。为使碳排放量和网络中的功率损耗最小，需限制各火力发电机出力和配电网与微电网的交换功率，故令PMT=PFC=PPDN=0；考虑到储能电池启动和关停成本，需限制其放电，令PSB=0；只由可再生能源向负荷供电，并将多余的能量提供给配电网以获取利润。

模式二：随着负荷的增加，当可再生能源无法满足负荷需求时需要启动储能电池，由可再生能源和储能电池共同出力来满足负荷需求。此时为使碳排放量和网络中的功率损耗最小，各火力发电机组的出力和配电网与微电网的交换功率仍为0。

模式三：当负荷继续增加，可再生能源与储能电池总量之和无法满足负荷需求时，需要启动各火力发电机组和配电网参与能量管理。此时上层模糊管理系统把信息通过通信通道传递给下层多目标函数优化层，在下层进行能量优化管理，其多目标优化数学模型见下文。

模式四：在极端条件下，当系统中所有储能电池、可再生能源、火力发电机都工作在最大输出功率状态，且微电网与配电网的交换功率达到上限。若此时输出功率仍不满足负荷需求，则将所有发电单元和主网交换功率均设置在最大临界工作模式，同时考虑切除部分负荷。

双层能量优化管理方法的具体流程如图2所示。其具体流程如下。

(1)向模糊管理控制层输入光伏出力PPV和风力发电机的出力PWT；每小时微电网负荷的需求PL。

(2)计算可再生能源整体发电量PRES=PPV+PWT。

(3)判断可再生能源出力PRES是否大于负荷需求PL，若PRES大于PL则微电网工作在模式一下，并执行步骤(6)，否则执行下一步。

(4)判断可再生能源出力PRES和储能电池最大出力PSBmax之和是否大于负荷需求PL，若PRES+PSBmax大于PL则微电网工作在模式二下，并执行步骤(6)，否则执行下一步。

(5)计算各火力发电机组最大出力之和PTGmax=PMTmax+PFCmax，判断微电网内所有机组最大出力和配电网的最大交换功率之和是否大于负荷需求PL，若PRES+PSBmax+PTGmax+PPDNmax大于PL，则微电网工作在模式三下，并对微电网进行多目标函数优化求解，执行步骤(6)。否则，微电网工作在模式四下，此时将所有发电单元和主网交换功率都设置在最大临界工作模式，同时考虑切除部分负荷。

(6)最终输出各火力机组PMT和PFC、储能电池PSB以及配电网PPDN的实时出力。

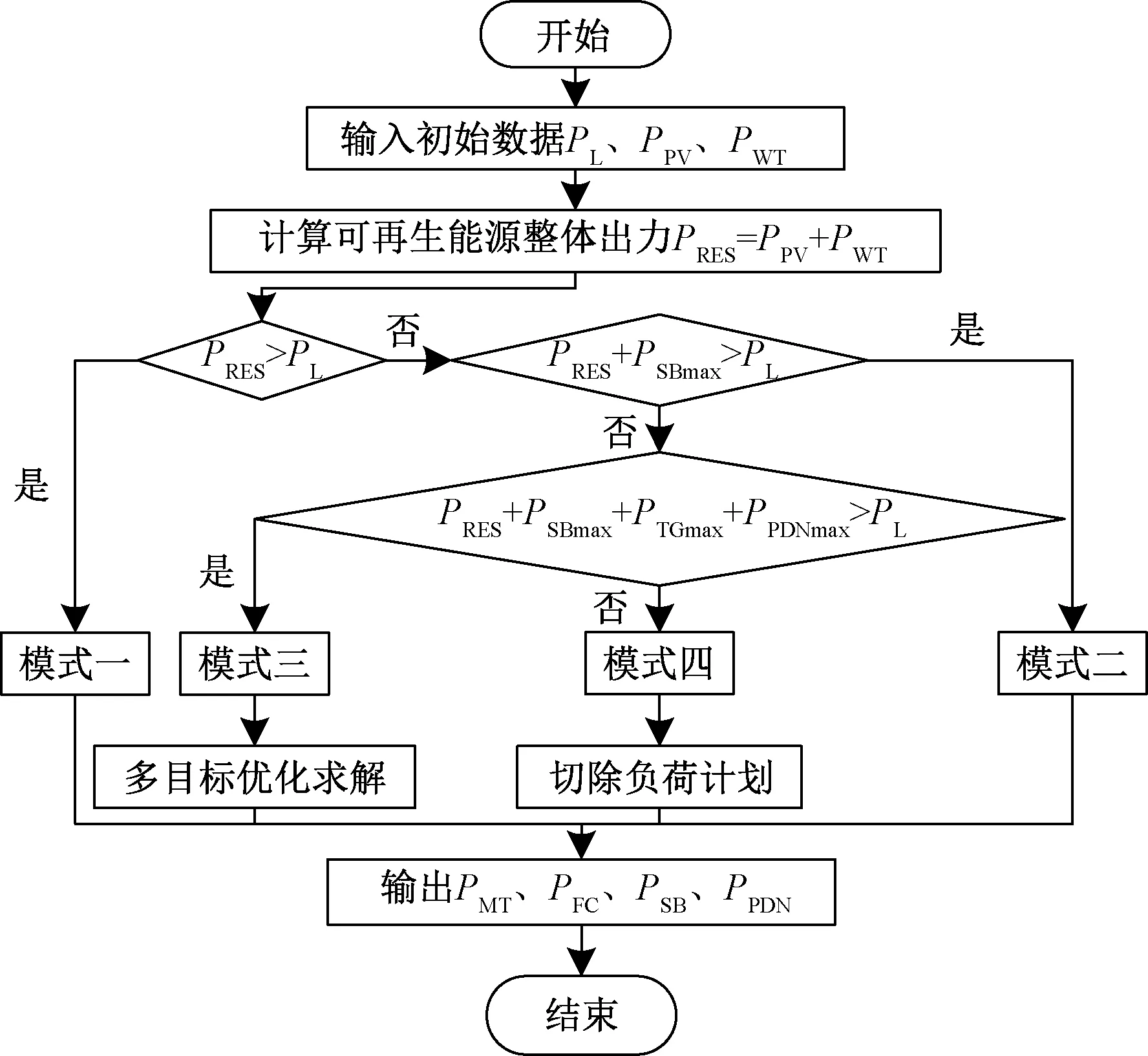
图2 能量优化管理系统流程图Fig.2 Flow chart of energy optimization management system

因此当系统处在模式一时，只需可再生能源向负荷供电，多余的能量将提供给配电网以获取利润。当系统在模式二下，储能电池和可再生能源共同向负荷供电。当系统在模式四下，微电网内各发电单元出力最大，同时执行切除负荷计划。因此处在模式一、模式二、模式四下的系统无需对微电网内各电源进行多目标函数优化求解。

由于系统大多处在模式三下，同时考虑各机组出力平衡，故该模式较为复杂。此时引入多目标优化方法，能量管理系统通过将上层信息传送给多目标函数优化层进行各分布式电源的容量求解。

2 微电网多目标优化数学模型

在并网条件下，将求解微电网内各分布式电源的容量问题转化为在等式约束和不等式约束条件下求解多目标函数最小值问题，其表达式为

(1)

式(1)中：f(t)为优化的目标函数；Cm(t)、fc(t)、Ploss(t)分别为微电网运行的成本-收益、碳排放量和有功功率损耗；hi(t)为等式约束；gi(t)为不等式约束。

2.1 微电网多目标函数

2.1.1 微电网运行成本-运行收益Cm(t)

微电网运行的经济性除了考虑投资成本外，还计及可再生能源、储能装置和各火力发电机组因售电而产生的收益。设微电网的投资成本为Cm1(t)，可再生能源、储能装置和火力发电机组产生的收益为Cm2(t)。则Cm(t)的表达式为

(2)

式(2)中：Cfuel(t)、Csud(t)分别为微电网的燃料成本和各单元的启停成本；CSB(t)、CRES(t)、CTG(t)分别为储能装置、可再生能源和各火力发电机组向微电网所带负荷售电产生的收益；CPDN(t)为混合微电网向配电网出售电能产生的收益。

投资成本主要由以下两部分组成。

(1)微电网的燃料成本Cfuel(t)。目前中国火力发电以MT和FC为主要发电单元，其燃料成本表达式通常以用具有正系数的二次多项式[12]表示,即

(3)

式(3)中：α、β、γ为MT和FC的成本系数；PMT(t)和PFC(t)分别为t时刻MT和FC的输出功率。

故微电网总的燃料成本为

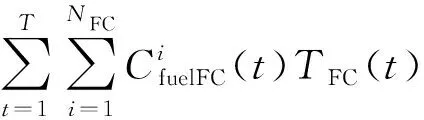
(4)

式(4)中：i为各火力发电机组数目；T为总的离散时间间隔T=24 h；NMT和NFC分别为MT和FC的总个数。

TP(t)为P机组的工作状态，其中P为MT或FC。

(5)

(2)各发电单元的启动或关闭成本Csud(t)。各发电单元的启动或关闭成本同本单元该时刻与前一时刻的工作状态有关，故其表达式[9]为

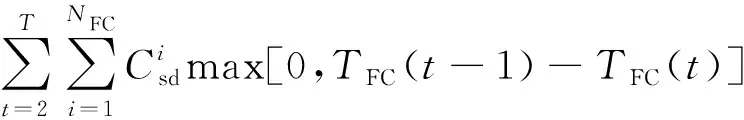
(6)

微电网产生的收益由以下4部分组成。

(1)储能电池提供电能的收益CSB(t)。储能电池向微电网负荷供电产生的收益CSB(t)为

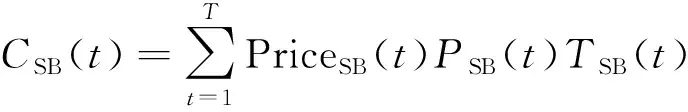
(7)

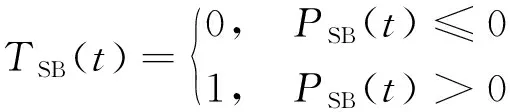
(2)可再生能源提供电能的收益CRES(t)。可再生能源向负荷供电产生的收益CRES(t)为

(8)

式(8)中：PriceRES(t)为t时刻可再生能源实时电价。

(3)各火力发电机组提供电能的收益CTG(t)。由于各火力发电机组以燃煤机组为主，故其向负荷出售的电价不随时间变化，可视其为定值。

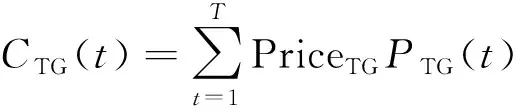
(9)

式(9)中：PriceTG为各火力发电机组出售电能的电价。

(4)与电网交换电能的收益CPDN(t)。混合微电网在并网条件下既可以处于购电也可以处于售电状态。由于微电网向配电网购买的电能会再次出售给微网负荷，故不考虑此电能产生的成本和收益，因此与电网交换电能的收益CPDN(t)为

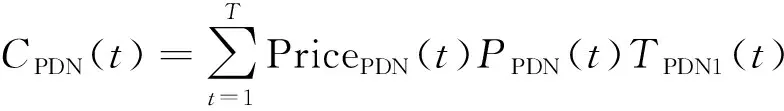
(10)

2.1.2 微电网的碳排放量fc(t)

由于微电网排放的污染物中二氧化碳所占比例最大[13]，故利用二氧化碳排放量fc(t)来衡量其对环境的影响。fc(t)的表达式为

(11)

式(11)中：fMT(t)、fFC(t)和fPDN(t)分别为MT、FC和PDN在t时刻碳排放量。

对于一台火力机组t时刻的碳排放量通常可以用具有正系数的一次多项式表示：

(12)

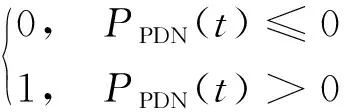
2.1.3 微电网的有功功率损耗Ploss(t)

由于混合微电网中线路阻抗较大，在功率传输时会产生相应的功率损耗。通常只考虑有功功率损耗，因此网络中功率损耗Ploss(t)的表达式为

(13)

式(13)中：Pij和Qij为线路ij上流经的有功和无功功率；Ui为节点i的电压幅值；Rij为线路ij的等效电阻。

2.2 分布式电源和配电网约束

2.2.1 等式约束条件

(1)功率平衡约束。

∑PL+∑Ploss=∑PRES+∑PSB+∑PTG+PPDN

(14)

式(14)中：ΣPL为微电网所带的总负荷；ΣPloss为总功率损耗；ΣPRES为可再生能源总功率；ΣPSB为储能电池总有功功率；ΣPTG为各火力发电机组总有功功率。

(2)单机容量与总发电量功率平衡约束。

(15)

2.2.2 不等式约束条件

(1)各火力发电机输出功率约束。MT和FC单位时间内发出的电能与各机组性能有关，其不等约束的数学表达式为

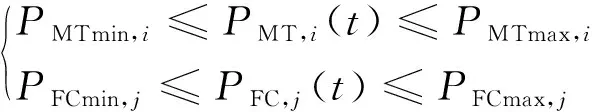
(16)

式(16)中：i,j=1,2，…，NG；PMTmin,i、PMTmax,i和PFCmin,j、PFCmax,j分别为i、j节点MT、FC功率限值。

(2)可再生能源发电量约束。光伏和风力发电机的输出功率PPV和PWT不等式约束条件满足：

(17)

式(17)中：PPV,MPPT和PWT,MPPT分别为光伏和风力发电机的最大输出功率。

(3)储能电池荷电状态及其功率约束。储能电池的出力情况由电池的荷电状态SOCp(t)表示，其约束条件为

SOCmin,p≤SOCp(t)≤SOCmax,p

(18)

式(18)中：SOCp为储能电池组p的电荷量。

由于储能电池的荷电状态SOCp(t)与电池的出力大小PSB(t)呈线性关系，因此储能电池充放电功率的约束关系为

-PSB,max,p≤PSB(t)≤PSB,max,p

(19)

式(19)中：PSB,max,p为储能电池组p的最大输出功率。

(4)微电网与配电网的电能交换约束。微网与配电网的电能交换约束表达式为

-PPDN,max≤PPDN(t)≤PPDN,max

(20)

式(20)中：PPDN,max为微电网与配电网交换的最大功率。

2.2.3 对约束条件的处理

对等式约束条件进行处理时，功率平衡约束采用潮流计算来保证；单机容量与总发电量功率平衡约束通过控制接入电网中的机组数量来保证[14]。对不等式约束条件进行处理时，在目标函数中引入罚函数，以确保最终结果在约束范围内。罚函数为

g=λ{max[(Pmin-P),0]+max[(P-Pmax),0]}

(21)

式(21)中：λ为充分大的惩罚因子；P为发电单元某一时刻的输出功率；Pmax、Pmin为输出功率的上、下限。

3 基于Tent混沌映射NSGA-Ⅱ算法

由于所建立的多目标优化模型中各目标之间相互制约，故选择全局收敛性较高的NSGA-Ⅱ算法进行求解[15-16]。该算法在NSGA算法基础上加入快速非支配排序方法、拥挤距离比较算子以及精英策略思想，使NSGA-Ⅱ算法以更快的速度对种群中个体进行非支配排序。但该算法通过随机采样进行种群初始化，会导致多极值的函数出现搜索盲区[17]。并且随着NSGA-Ⅱ算法的迭代次数不断增加，精英策略思想使局部最优解出现遗传优势，导致种群中新个体的数量减少而陷入局部最优[18]。因此利用Tent混沌映射方法对NSGA-Ⅱ算法进行改进。

3.1 混沌初始化及混沌搜索

首先利用混沌方法对种群进行初始化。一般采用Logistic映射，但由于Logistic映射遍历不均匀且迭代速度较慢，因此采用结构简单、具有良好的遍历均匀性且迭代速度较快的Tent混沌映射，其映射方程[19]为

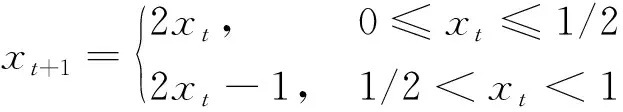
(22)

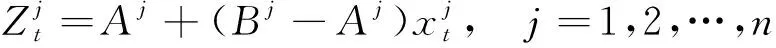
(23)

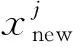
(24)

3.2 改进的NSGA-Ⅱ算法实现

改进NSGA-Ⅱ算法的具体步骤[14,20]如下。

(1)输入基础数据，其中包括种群中个体数量N，最大迭代次数maxgen，变异率Pc和交叉率Pm。

(2)在[0，1]区间内随机产生矩阵xt，由式(22)计算得混沌序列{xt}，代入式(23)形成父代种群Pt。

(3)计算父代种群Pt中所有个体的目标函数，调用NSGA-Ⅱ算法进行快速非支配排序，得到种群分级支配虚拟适应度。通过得到的适应度计算每个非支配层个体的拥挤距离，并再次进行排序。

(4)利用二元锦标赛方法对父代种群进行算子的选择、交叉和变异，生成子代种群Ot。

(5)为提高种群多样性，再生成N/5个混沌个体Qt，并将种群Pt、Ot、Qt合并生成混合种群Rt。对种群Rt进行快速非支配排序、拥挤距离比较及精英策略，从中选出前N个个体组成新的父代种群P′t。

(6)从父代种群P′t中选出前10%精英个体，通过式(24)进行混沌搜索得到搜索后的新个体。如果产生的新个体更优，则用新产生的个体替换种群P′t中原来的个体，得到更新后的父代种群Pt+1。

(7)重复循环步骤(4)～步骤(6)，直到达到最大迭代次数tmax后终止该算法，得到Pareto最终解集。

3.3 最优解的选取

为了从Pareto最终解集中选出最优解，故引入模糊隶属度函数。通过式(25)和式(26)计算最终解集中第m个解对应的第i个目标函数的隶属度μi(m)以及聚合函数μ(m)，其表达式为

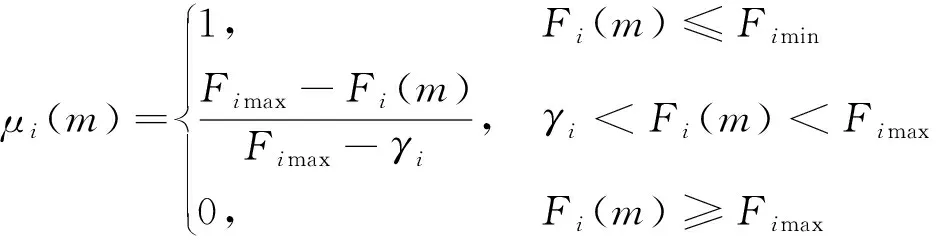
(25)

γi=Fimax-θi(Fimax-Fimin)， 0≤θi≤1

(26)

式中：Fimax和Fimin分别为第i个目标函数的限值；Fi(m)为第m个解对应的第i个目标函数值，其中目标函数F1(m)为微电网运行成本-运行收益；F2(m)为微电网碳排放量；F3(m)为微电网网络损耗；θi为第i个目标函数所占比重；i=1,2,3且m=1,2，…，N。

决策者可根据不同地区、不同时间对微电网运行的负荷需求确定θi的具体值。综合考虑多目标函数下的能量优化管理，提出将微电网运行的经济性、碳排放量和有功功率损耗相互平衡作为目标期望最优解,设θ1=θ2=θ3=1。由三个隶属度函数求得聚合函数μ(m)，将μ(m)数值最大的解作为最优解。

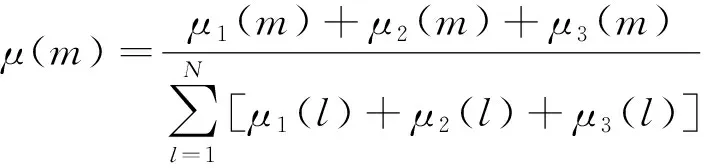
(27)

4 算例分析

以图3低压测试网络为例，验证所提出的双层能量优化管理方法、容量配置优化模型以及改进NSGA-Ⅱ算法的有效性。

其中改进算法的仿真参数，以及配电网和各分布式电源的机组出力范围、碳排放量和机组的启停成本等运行参数如表1和表2所示。

图4和图5分别给出了一天内可再生能源的预测发电量、住宅负荷需求和出售电能的实时电价。

1～17为不同的节点编号图3 低压测试网络Fig.3 Low voltage test network

表1 改进的NSGA-Ⅱ算法的仿真参数

表2 配电网和各分布式电源的运行参数

图4 可再生能源预测发电量和住宅负荷计划需求Fig.4 Forecast electricity generation and housing load planning demand for renewable energy

图5 实时电价Fig.5 Real-time electricity price

4.1 上层模糊管理系统优化结果对比分析

根据文中提出的上层模糊管理系统，在给出的测试网络和数据的基础上，得到一天内不同机组出力及负荷需求对比图，如图6所示。

图6 上层模糊管理系统工作模式Fig.6 Working mode of fuzzy management system

由图6可知，可再生能源与储能电池总量之和已无法满足负荷需求，因此需要启动相应火力发电机组和配电网参与能量管理。即该欧洲一典型微电网全天24 h内均工作在模式三下，此时需要对各火力发电机、储能电池和配电网的出力进行多目标函数优化求解。说明在文中所提出的能量管理系统模型中建立下层多目标函数优化层的必要性。

4.2 下层多目标函数优化结果对比分析

4.2.1 Pareto最终解集和各机组最优出力的确定通过图9可以看出，用户在0：00—7：00对电能需求较低，微电网的输出功率几乎可以满足负荷需求，故只需从配电网购买少量电能。在5：00—6：00点间居民用电负荷处于低谷期，故微电网可将多余的电能出售给配电网以产生收益。由于微电网中各火力发电机组和配电网的出力随居民用电负荷变化，在19：00—22：00用电高峰期可再生能源出力逐渐减小，火力发电机和配电网出力不断增加，考虑火力机组产生的二氧化碳对环境的影响，因此需要配电网参与电能的优化管理，在此期间微电网与配电网的电能交换达到峰值。由优化结果可以看出，一天内储能电池出力波动范围较小，有利于延长电池寿命。

综合考虑文中所提出的三个目标函数，采用改进NSGA-Ⅱ算法对该低压测试网络进行多目标函数优化求解，得到如图7和图8所示的三维和二维Pareto最终解集，及如图9所示的各机组最优出力。

图7 改进NSGA-Ⅱ算法三维Pareto最终解集Fig.7 3D Pareto final solution set of improved NSGA-Ⅱ algorithm

图8 改进NSGA-Ⅱ算法二维Pareto最终解集Fig.8 2D Pareto final solution set of improved NSGA-Ⅱ algorithm

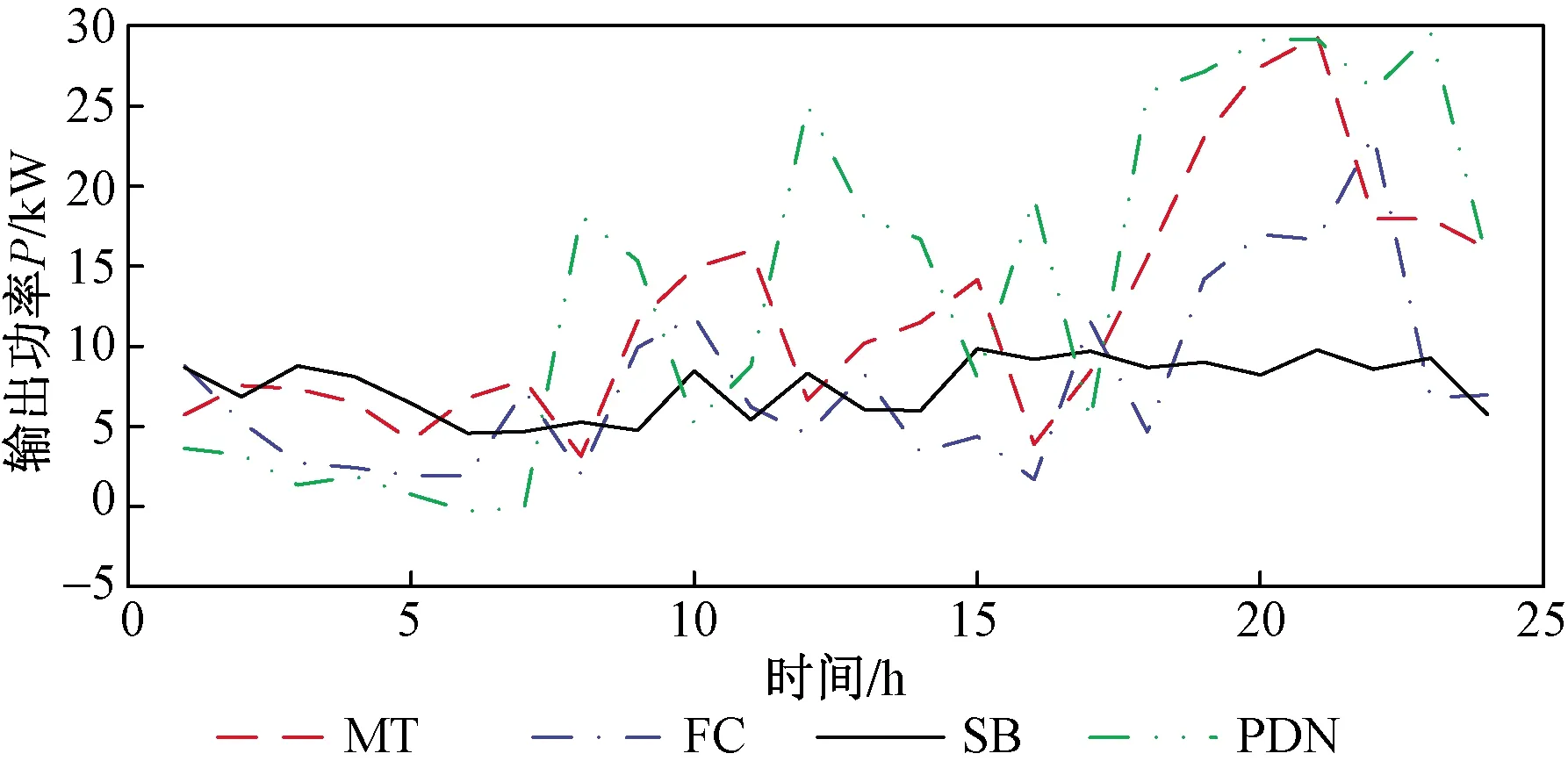
图9 各机组最优出力Fig.9 Optimal output of each unit

4.2.2 与传统NSGA-Ⅱ算法比较

利用传统NSGA-Ⅱ算法，仿真得到如图10和图11所示的三维和二维Pareto最终解集。

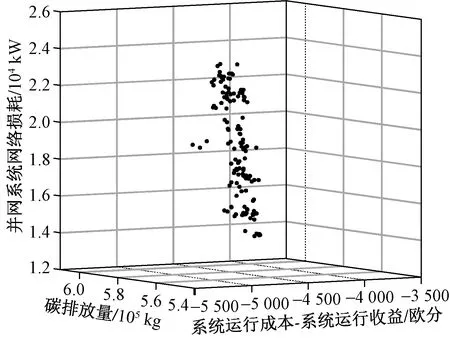
图10 传统NSGA-Ⅱ算法三维Pareto最终解集Fig.10 3D Pareto final solution set of traditional NSGA-Ⅱ algorithm

图11 传统NSGA-Ⅱ算法二维Pareto最终解集Fig.11 2D Pareto final solution set of traditional NSGA-Ⅱ algorithm

由图7和图10的对比分析可知，基于Tent混沌映射NSGA-Ⅱ算法增加了种群多样性，使三个目标函数对应的Pareto最终解集相比NSGA-Ⅱ算法得到的解集分布更广且更均匀，更好地优化了Pareto前沿。通过对比图8(a)和图11(a)系统运行经济性-网络损耗二维图可以看出，改进的NSGA-Ⅱ算法得到的Pareto最终解集构成的曲面较为平坦，降低了结果的波动性。从图8(b)和图11(b)碳排放量-网络损耗二维图以及图8(c)和图11(c)系统运行经济性-碳排放量二维图看出，当微电网的目标函数较复杂时，改进的NSGA-Ⅱ算法计算得到的Pareto最终解集分布范围较大，算法全局搜索能力较高，不易导致最终解集陷入局部最优。有效地证明了利用改进的NSGA-Ⅱ算法求解多目标优化数学模型的优越性。

分别利用两种算法对低压测试网络的多目标优化数学模型进行求解，得到的三个目标函数值如表3所示。

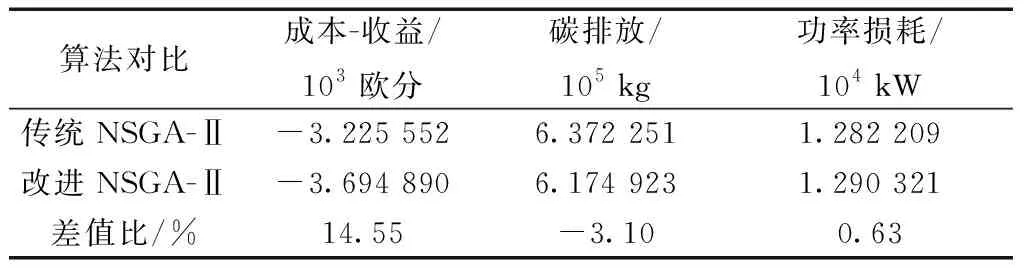
表3 两种算法优化结果

对比表3中改进NSGA-Ⅱ算法与传统NSGA-Ⅱ算法所得的结果不难发现，在两者的功率损耗近似相等的情况下，改进NSGA-Ⅱ算法具有良好的优化效果，使得微电网运行的经济性得到了显著提升，较传统算法提高了14.55%；碳排放量有所降低，较传统算法减小了3.10%。证明了基于Tent混沌映射NSGA-Ⅱ算法在处理多目标优化问题上更具优越性。