两端刚接梁在三种不同荷载布置下的传递系数计算
2022-06-14周陈程俞海洪耿志光
周陈程,俞海洪,耿志光
(中石化上海工程有限公司,上海 200120)
石油化工[1]是典型的高危生产行业,其装置的生产条件常伴有高温高压,且在生产、输送、存储过程中所需处理的原材料、半成品、催化剂、溶剂等绝大多数属于易燃易爆介质,这些介质在工艺流程中常以气态或液态存在,极易发生泄漏,造成重大的爆炸事故。近年来,我国石油化工装置的产能和规模持续扩大,装置发生爆炸的可能性和危害性也在同步升级。为了有效保护在爆炸冲击波作用下人员的安全、保障重要设备(设施)的正常运行,石油化工装置内重要建筑物如中央控制室,应进行抗爆设计[2]。目前建筑物抗爆设计通常有四种方法:等效静载法、等效单自由度动力分析法、理论分析法、有限元整体分析法。等效静载法是早期发展起来的一种静态分析方法,它采用近似的静载来模拟动态响应,一般适用于远场爆炸,这种方法最大的问题在于如何确定适当的等效静载,部分规范[3]已不再推荐使用此方法。理论分析法[4-5]是根据边界条件和荷载条件,计算出构件运动的精确解,但由于其计算理论复杂、过程繁琐,使其在实际工程应用中受到了很大限制。有限元整体分析法是一种近些年快速发展的计算方法,但是建立精细化网格模型工作量大、计算时间长、模型计算结果对模型参数、材料参数很敏感,如果设计人员在数值模拟方面没有丰富经验,很难对计算结果的准确性进行判别。等效单自由度动力分析法是现阶段抗爆设计中最常用的计算方法,该方法首先由Norris[6]和Biggers[7]提出,具有概念清晰、计算简单等优点,美国陆军防护设计中心基于此方法专门开发了单自由度毁伤评估设计软件SBEDS[8]。
等效单自由度动力分析计算中关键一步就是对梁、板、墙等构件进行单自由度的等效转换,包括荷载、质量和刚度,其中等效荷载和等效质量需要根据实际荷载和质量的大小、分布情况以及荷载传递系数、质量传递系数确定。目前国内外规范、文献[2-3]给出的荷载传递系数、质量传递系数基本都是基于biggers 的文献[7],但是该传递系数表格不够完善,实际工程中常碰到荷载分布超出表格适用范围的情况,且该表格部分数据存在错误。本文以文献[7]的研究为基础,对两端刚接梁在三种不同荷载布置工况的传递系数进行推导分析,并对表格中部分数据进行纠正和扩充。
1 荷载和质量传递系数的计算方法
等效单自由度动力分析中荷载和质量传递系数是基于实际体系和等效体系能量守恒原理推导而来,其中荷载传递系数满足实际结构构件与单自由度系统的荷载做功相同,质量传递系数满足实际结构构件与单自由度系统的动能相同。
1.1 荷载传递系数KL
连续分布载荷:
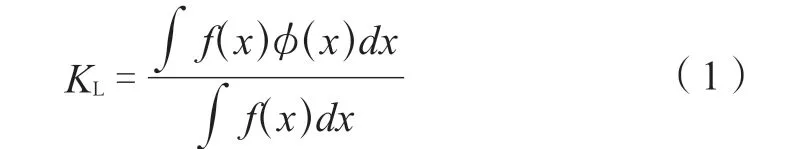
若干个集中载荷:
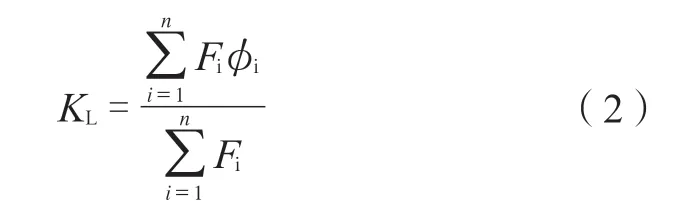
式中φ(x)、φi——构件形状函数;
f(x)——构件的荷载分布函数;
Fi——集中荷载;
n——构件计算长度内集中荷载数量。
1.2 质量传递系数KM
连续分布质量:
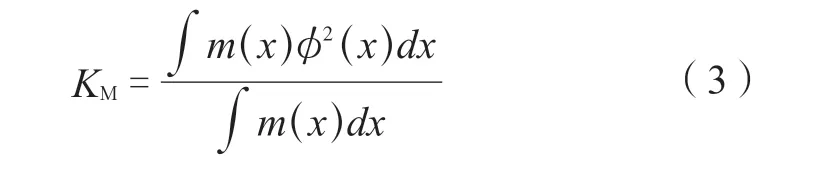
若干个集中质量:

式中m(x)——构件的质量分布函数;
Mi——集中质量;
n——构件计算长度内集中质量数量。
1.3 形状函数
构件的形状函数由其一阶振动模态确定,通常可由其归一化后的静态挠度曲线函数代替[7]:

式中f(x)——构件的挠度曲线函数;
fmax——构件的最大挠度。
本文的静态挠度曲线拟采用挠度曲线近似微分方程求解,即y*=M(x)/EI;挠度曲线近似微分方程略去了(dy/dx)2项。按GB 50779—2012《石油化工控制室抗爆设计规范》表5.6.4 的规定,结构构件的最大允许转角4°,此时:
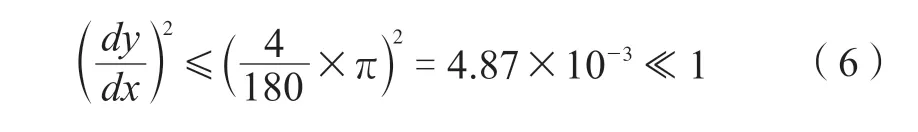
即在结构构件发生规范允许最大转角时,挠度曲线近似微分方程的解也能满足工程设计的精度要 求。
2 三种不同荷载布置的传递系数计算
2.1 两个集中载荷对称布置
两个集中载荷对称布置的荷载简图见图1,该荷载作用下不同阶段的静态挠度曲线见图2。

图1 两个集中载荷对称布置荷载简图Fig.1 Schematic diagram of two concentrated loads arranged symmetrically

图2 两个集中载荷对称布置的静态挠度曲线Fig.2 Static deflection curve of two concentrated loads arranged symmetrically
2.1.1 形状函数
根据挠度曲线近似微分方程可以求得不同阶段的形状函数,如下:
弹性阶段:

弹塑性阶段:

塑性阶段:

式中α=a/L,α∈(0,1/2]。
当x=a和x=L-a时,
弹性阶段:

弹塑性阶段:
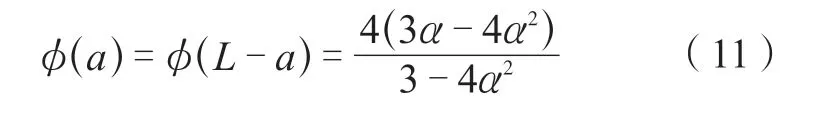
塑性阶段:
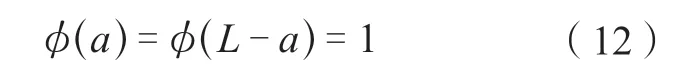
2.1.2 荷载传递系数
将式(10)~(12)分别带入式(12),得到:
弹性阶段:

弹塑性阶段:

塑性阶段:

2.1.3 均布质量传递系数
将式(7)~(9)带入式(3),可以得到:
弹性阶段:

弹塑性阶段:
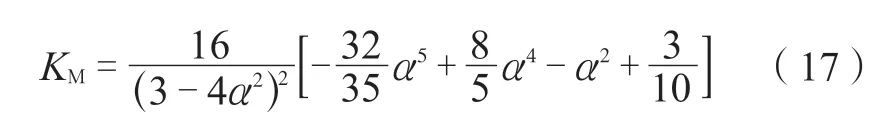
塑性阶段:

2.1.4 集中质量传递系数
将式(10)~(12)分别带入式(4),得到:
弹性阶段:

弹塑性阶段:

塑性阶段:

2.1.5 数据对比分析和验证
当α= 1/2 和α= 1/3 时,荷载传递系数和质量传递系数如下表1。
表1 中数据与文献[9]基本一致,只在α= 1/3 时,弹塑性阶段的均布质量传递系数 值存在差异(表中“*”),对于弹塑性阶段,此时构件两端出现塑性铰,即两端铰接情况,根据David Cormie 等[10]对biggers的文献[7]中两端铰接,集中载荷作用在1/3 跨处的均布质量传递系数KM的纠错,正确值应该是0.50,与本文结果一致。同时把表1 数据与GB 50779—2012《石油化工控制室抗爆设计规范》[2]附录B 比较可以看出,规范中两端铰接弹性阶段集中荷载作用在1/3 跨处的均布质量传递系数KM、一端铰接一端刚接的弹塑性阶段集中荷载作用在1/3 跨处的均布质量传递系数KM以及两端刚接的弹性阶段集中荷载作用在1/3 跨处的荷载传递系数KL、集中质量传递系数KM、均布质量传递系数KM都存在错误。

表1 α=1/2、α=1/3 的构件荷载和质量传递系数Tab.1 Load and mass transfer coefficients of two concentrated loads arranged symmetrically under α = 1/2 and α = 1/3
2.2 三个集中载荷均匀布置
目前随着装置规模的不断扩大,控制设备也在不断增多,为了更好地满足操作台的布置和空间感的协调,大跨度中央控制室在工程中日益常见。原规范中两个集中载荷均布已无法满足大跨度中央控制室的抗爆设计需求。所以本节主要对三个集中载荷均布的传递系数进行推导,更多集中载荷均布的传递系数可参照此方法进行计算。
三个集中载荷均匀布置可采用叠加法原理进行计算,其荷载简图见图3,该荷载作用下,不同阶段的静态挠度曲线如图4。

图3 三个集中载荷均匀布置荷载简图Fig.3 Schematic diagram of three concentrated loads arranged uniformly

图4 三个集中载荷均匀布置的静态挠度曲线Fig.4 Static deflection curve of three concentrated loads arranged uniformly
2.2.1 形状函数
根据挠度曲线近似微分方程可以求得不同阶段的形状函数,如下:
弹性阶段:
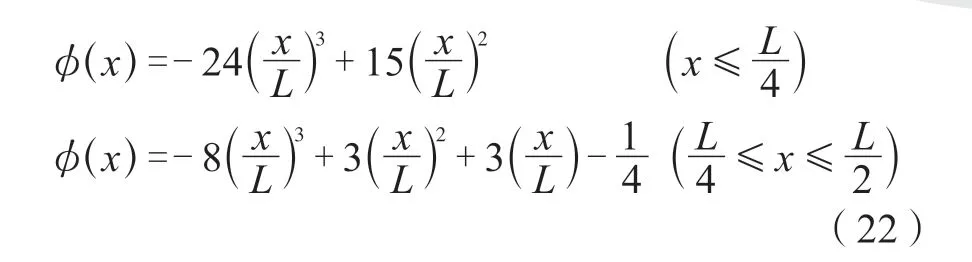
弹塑性阶段:
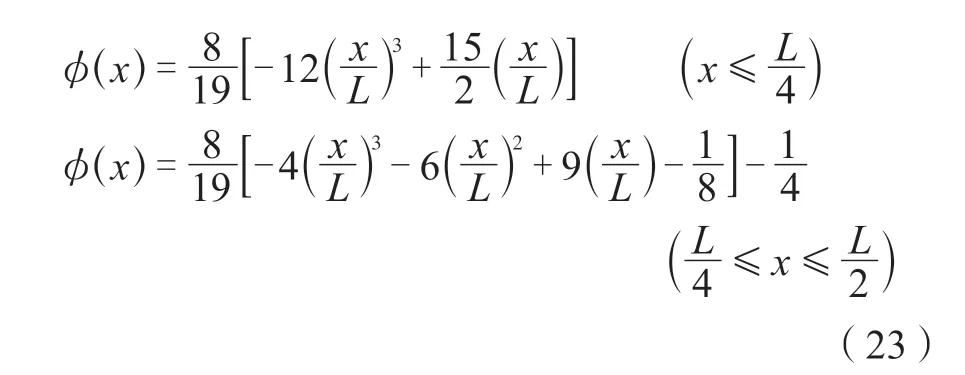
塑性阶段:

当x=L/ 4、x=L/ 2、x= 3L/ 4 时
弹性阶段:
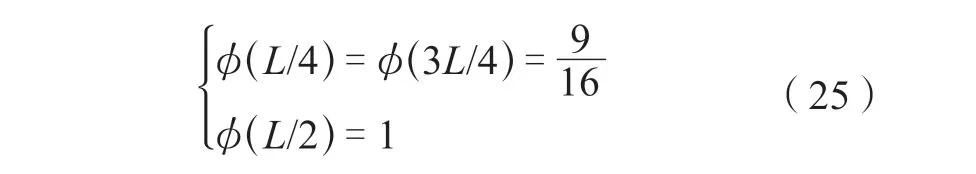
弹塑性阶段:

塑性阶段:
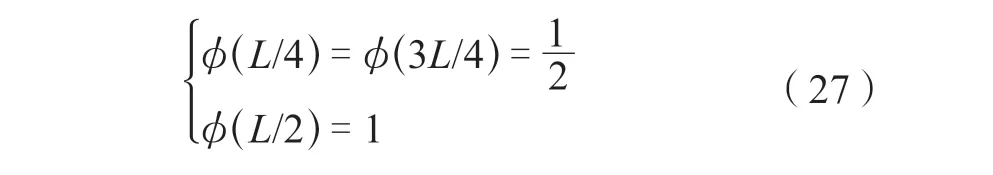
2.2.2 荷载传递系数和质量传递系数
将式(25)~(27)分别带入式(2),得到不同阶段的荷载传递系数KL,详见表2。
将式(25)~(27)分别带入式(4),得到不同阶段的集中质量传递系数KM,详见表2。
将式(25)~(27)分别带入式(3),得到不同阶段的均布质量传递系数KM,详见表2。

表2 三个集中载荷均布的荷载和质量传递系数Tab.2 Load and mass transfer coefficients of three concentrated loads arranged uniformly
2.3 对称三角形载荷布置
对称三角形载荷布置的荷载简图见图5,该荷载作用下不同阶段的静态挠度曲线见图6。
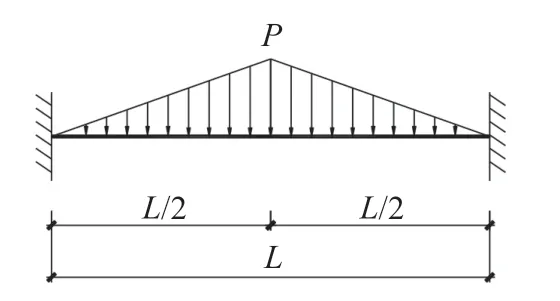
图5 对称三角形载荷布置荷载简图Fig.5 Schematic diagram of triangular loads arranged symmetrically

图6 对称三角形载荷布置的静态挠度曲线Fig.6 Static deflection curve of triangular loads arranged symmetrically
2.3.1 形状函数
根据挠度曲线近似微分方程可以求得不同阶段的形状函数,如下:
弹性阶段:
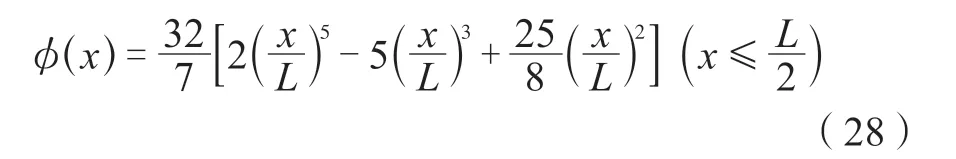
弹塑性阶段:
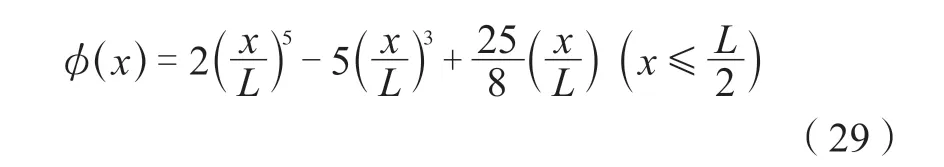
塑性阶段:

2.3.2 荷载传递系数和质量传递系数
荷载分布函数:

将式(28)~(30)及式(31)分别带入式(1),得到不同阶段的荷载传递系数KL,详见表3。
将式(28)~(30)分别带入式(3),得到不同阶段的均布质量传递系数KM,详见表3。

表3 对称三角形载荷的荷载和质量传递系数Tab.3 Load and mass transfer coefficients of triangular loads arranged symmetrically
3 结论
(1)根据构件最大允许转角限值,验证了挠度曲线近似微分方程求解的形状函数能满足抗爆设计的精度要求。
(2)对两端刚接梁在三种工程中常见荷载布置工况但规范未明确的传递系数进行推导分析,给出了荷载和质量传递系数计算公式和计算值,三种不同荷载布置工况包括:两个集中载荷对称布置、三个集中荷载均匀布置以及对称三角形载荷布置。
(3)通过对两个集中载荷对称布置的计算结果验证分析,指出规范[2]附表中的多处错误数据,并对附表中缺失的弹塑性阶段传递系数进行了补充。
(4)基于两个集中载荷对称布置传递系数计算公式,采用叠加法原理推导出三个集中荷载均匀布置的传递系数值,此方法还可以推广至N 个集中载荷均匀布置的传递系数求解。
等效单自由度动力分析是抗爆设计最常用的设计方法,但是目前规范[2]给出的各种不同荷载分布的传递系数已经无法满足日益复杂的结构体系,急需对传递系数表格进一步扩充和完善。
