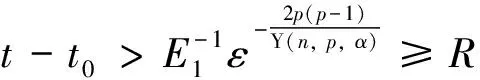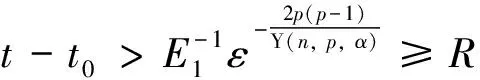一类系数依赖于时间的非线性项的半线性双波动方程解的爆破研究①
2022-06-14欧阳柏平
欧阳柏平
广州华商学院 数据科学学院, 广州 511300
近年来, 有关半线性波动方程柯西问题的研究受到广泛的关注. 有很多学者[1-9]研究了如下波动方程的柯西问题
(1)
其中p>1,n≥1和u=u(t,x)∈R,ε>0.
众所周知, (1)式中的临界指数Pcrit(n)即Strauss指数在波动方程解的全局性与爆破研究中起着重要作用. (1)式中的临界指数Pcrit(n)由下面一元二次方程的正根表示
也就是
对于n=1, 有Pcrit(1)=∞.
对于(1)式的研究, 学者们主要采用的方法是基于微分不等式和Kato引理. 然而, Kato引理只适用于二阶的微分方程, 对于高阶的波动方程(比如四阶), 则需要寻找其他的办法. 近来有学者采用迭代办法研究了某些双曲方程解的全局性和爆破问题[10-16]. 有关其他的偏微分方程解的爆破问题研究可参考文献[17-19].
本文研究如下系数依赖于时间的非线性项的半线性双波动方程解的爆破问题
(2)
其中f(t)=(1+t)-α, 0<α<2,p>1,ε>0, Δ是拉普拉斯算子.
目前, 有关高阶的半线性双波动方程柯西问题解的爆破研究尚未得到展开. 其主要难点在于如何构造测试函数通过迭代方法来解决高阶波动方程柯西问题研究中出现的问题. 本文通过选取合适的测试函数进行迭代得到了在非临界情况下系数依赖于时间的非线性项的半线性双波动方程解的上界估计.
首先给出(2)式的柯西问题能量解的定义
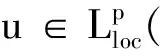
(3)
对于(3)式, 由分部积分可得
(4)
令t→T, 则u满足(2)式定义的弱解的定义.
1 本文主要结果
定理1设
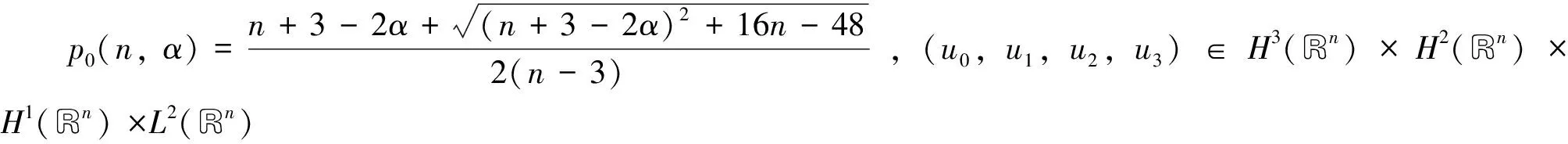
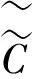
Y(n,p,α)=(n+3-2α)p+4-(n-3)p2
(5)
2 爆破时间的上界估计
设
(6)
(4)式中, 取φ≡1, {(s,x)∈[0,t]×Rn: |x|≤R+s}, 可得
(7)
联立(6),(7)式, 得到
(8)
对(8)式关于t积分3次, 可得
(9)
因为支集u(t, ·)⊂Bt+R, ∀t∈(0,T), 由Hölder不等式, 可得
(10)
由(9),(10)式, 可得
(11)
下面将通过对U(t)的下界进行迭代完成定理的证明. (11)式确定了迭代的框架. 为了推导U(t)的第一个下界估计, 引入如下函数[20]
函数Φ(x)是正的, 并且有下面的性质
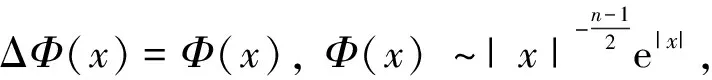
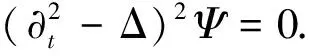
定义辅助函数
(12)
对(8)式关于时间t求导数, 得
(13)
应用Hölder不等式于(12)式, 得到
(14)
将测试函数Ψ应用到(3)式, 有
(15)
对(15)式分部积分并注意到Ψ的性质, 可得
(16)
其中
联立(12)式和(16)式, 得
(17)
设
于是, (17)式可化为
F′(t)+2F(t)≥εI[u0,u1,u2,u3]
(18)
对(18)式积分, 得
(19)
由(19)式和F(t)的定义, 有
(20)
对(20)式关于t求积分, 可推出
(21)
其中δ=min{1-e-2t,te-2t}.
由定理的条件, 可得当t≥t0时, 有
(22)
由Ψ的渐近性, 可得
(23)
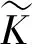
由(14),(22)和(23)式有
(24)
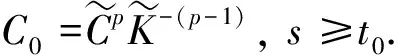
联立(13)和(24)式可得
(25)
其中t≥t0.
对(25)式求积分, 有
(26)
(26)式可记为
U(t)≥K0(R+t)-α0(t-t0)β0
(27)
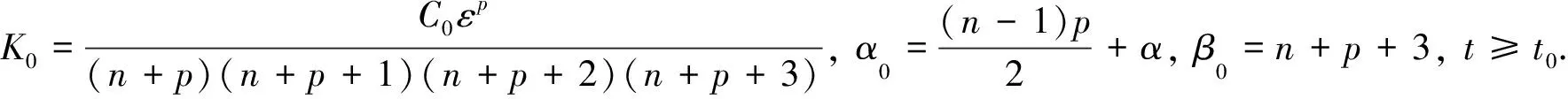
接下来, 将通过迭代来推导U(t)的下界
U(t)≥Kj(R+t)-αj(t-t0)βj
(28)
其中非负实序列{Kj}j∈N, {αj}j∈N, {βj}j∈N将在下文定义.
联立(11)和(28)式, 得
(29)
接着取
(30)
则(29)式可化为
U(t)≥Kj+1(R+t)-αj+1(t-t0)βj+1
(31)
(31)式表明(28)式对于j+1是成立的. 接下来, 将对Kj,αj,βj进行估计.
由(30)式有
(32)
又由于
(33)
联立(30)和(33)式, 得到
(34)
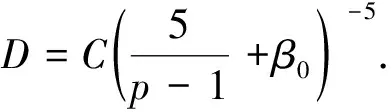
对(34)式两边取对数可得
(35)
令j0=j0(n,p)∈N为满足
的最小正整数, 从而, 对于j≥j0, 由(35)式可得
(36)
其中E0=E0(n,p)>0.
联立(28),(32)和(36)式, 得到
(37)
其中j≥j0,t≥t0.
当t≥R+2t0时, 有log(R+t)≤log(2(t-t0)). 于是(37)式化为
(38)
其中t-t0的指数为
(39)
由于0<α<2, 当n=1,2,3时,p>1; 当n≥4时, 1 取ε0=ε0(u0,u1,u2,u3,n,p,α,R)>0, 使得 从而证明了定理1.