基于模拟退火遗传算法的AGV调度系统研究
2022-06-14余星宝杨慧斌周玉凤
余星宝,杨慧斌,周玉凤
(上海工程技术大学机械与汽车工程学院,上海 201620)
1 引言
我国正处于“中国制造2025”的关键阶段[1],航空航天领域一直处于国家战略性地位,也代表了一个现代工业化国家的技术水平。为了提高装配和加工效率,航空公司借鉴福特公司的汽车装配流水线,改造出了“脉动生产线”,大大缩短了大型航空件如飞机的生产时间,同时对飞机零部件的装配要求也更高。采用麦克纳姆轮的自动引导车(AGV)可以全向移动,因此采用麦克纳姆轮重载AGV应运而生,不仅可以灵活满足普通的搬运任务,而且还可以在重载AGV的基础上搭载具有其它功能的机器人对航空件进行各种工艺操作,提高生产效率。
对于重载AGV的研究,国内外对重载AGV的主要研究方向是机械结构方面和误差方面的研究[2],许多专家学者也对AGV的调度研究进行了大量研究。针对降低运输时间、提高调度效率方面,采取现代优化算法,如遗传算法[6]、模拟退火算法等[7]。曹有辉等[8]针对AGV局部极小值问题,提出一种基于虚拟目标的人工势场的路劲规划算法,罗哉等[9]利用积分分离PID纠偏算法来对AGV轨迹偏差进行纠正,杨玮等[10]采用混合粒子群算法减低AGV调度过程中产生的锁死现象;对于小车调度的评判方法,如模糊评价法[11]、数据包络法[12]等。
本文结合某公司的重载钻铆AGV,对重载AGV的调度系统进行研究,针对调度系统的稳定性,提出理想解法对AGV进行实时评价建模,得到适应度函数。然后利用模拟退火遗传算法对多AGV调度进行试验和仿真,对本文所采用的方法的实用性和有效性进行验证。
2 问题描述和建模
2.1 问题描述
本文研究的自动钻铆移动机器人,加工对象为飞机水平尾翼,加工部位如图1所示,主要集中在上前壁板、上后壁板连接处;上后壁板与前梁连接部分;上前壁板外半侧与后梁连接部分(绿色点集区域)。
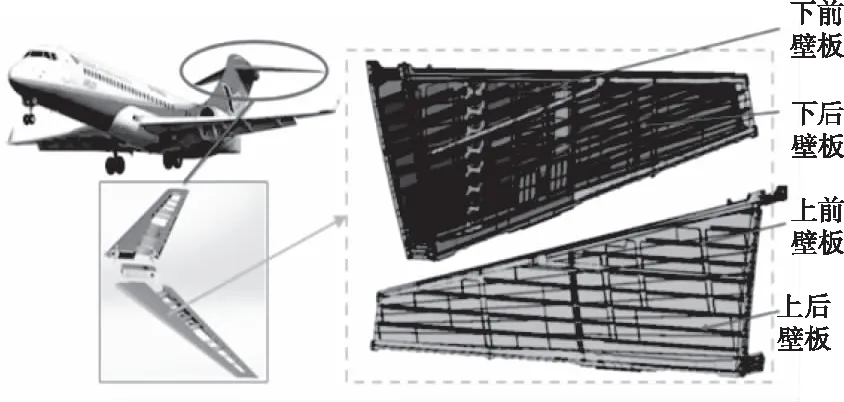
图1 加工对象
主要组成为重载AGV、钻铆外末端执行器、内顶执行器与制孔末端执行器,其模型如图2所示。主要工艺流程是自动钻孔、自动测量和自动铆接等其它工艺如图2和图3所示,被加工部分即为固定工装部分。

图2 钻铆机器人工作模型

图3 钻铆AGV实物
作业车间的调度问题可以描述为:有N台钻铆机器人和M个工装,每一个工装所需工序时间相同。加工完一个工序之后AGV可以选择继续加工或者去下一个工装进行加工。并且做如下假设:
1)AGV具有相同的运动速度,以避免AGV因速度不一致而产生同向碰撞冲突。
2)AGV的最短路径已经规划好,AGV数量固定,每个工装的加工时间相同。
3)每个工装AGV只加工一次,不允许重复加工。
2.2 基于理想解法建立目标函数
2.2.1 单AGV完成一项任务时间
首先计算出移动机器人完成一次钻铆所需的时间;然后利用理想解法的方式[13],将AGV当前电量、铆钉数量作为评价因素,计算出评价因子,目标函数即为评价因子与单个任务时间的乘积。本文建立模型来计算AGV移动至工装的最短时间。一台AGV在完成一次钻铆任务的总耗时T如式(1)所示
T=Te+Twl+Tij+Twg,Te≥0,Twl≥0,Tij≥0,Twg≥0
(1)
其中,T代表单AGV完成一次钻铆任务的总时间;AGV接受指令有两种情况:1.当前时刻AGV无钻铆任务,Te表示AGV没有任务的等待时间;2.AGV正在钻铆,耗时Twl之后AGV可以结束现阶段的任务;Tij代表AGV从工装i到达工装j的时间;Twg代表AGV完成钻铆任务的时间。AGV结束所有钻铆任务需要的时间如式(2)所示

(2)

(3)

(4)
2.2.2 建立理想解法评价评价函数
由于2.2.1章节的AGV调度模型只考虑了调度时间,并没有考虑电量不足或者铆钉数量不够等情况,导致整个系统缺乏鲁棒性。为了应对这些问题,本文提出理想解法评价模型(也称TOPSIS法)。假设AGV当前状态如表1所示。

表1 AGV当前状态数据
1)数据预处理。将AGV当前电量和当前铆钉数量相应数据放入矩阵aij中,向量标准化按照式(5)进行处理。

(5)
数据经过处理之后的结果如表2所示。
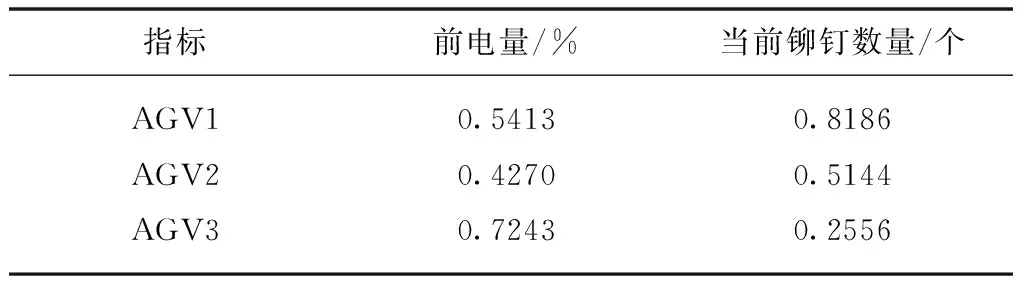
表2 数据经标准化的属性表
2)设置权重系数。设权重向量为w=[0.6,0.4],在设置权重系数之后,当前电量和铆钉数量向量规范属性如表3所示。
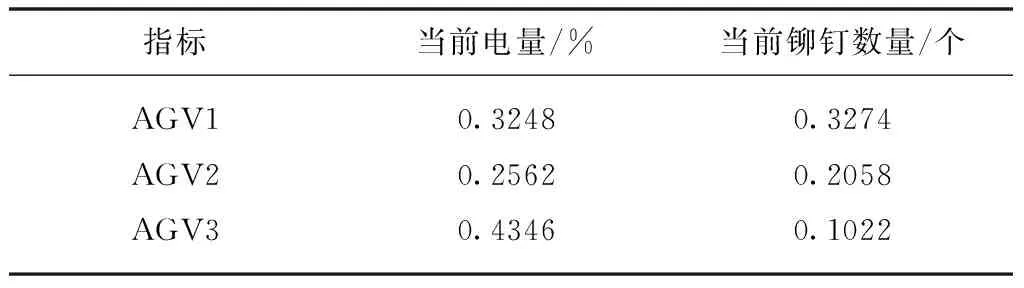
表3 加权标准化属性表
3)确定正理想解C*和负理想解C0。
正理想解如式(6)

(6)
负理想解如式(7):
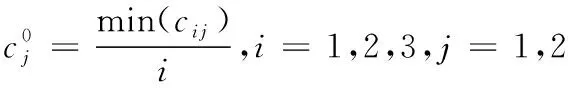
(7)
由表3、式(6)和式(7)可知,正理想解C*=[0.4346,0.3274],负理想解C0=[0.2562,0.1022]。
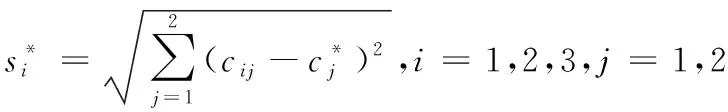
(8)

(9)

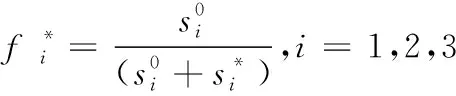
(10)
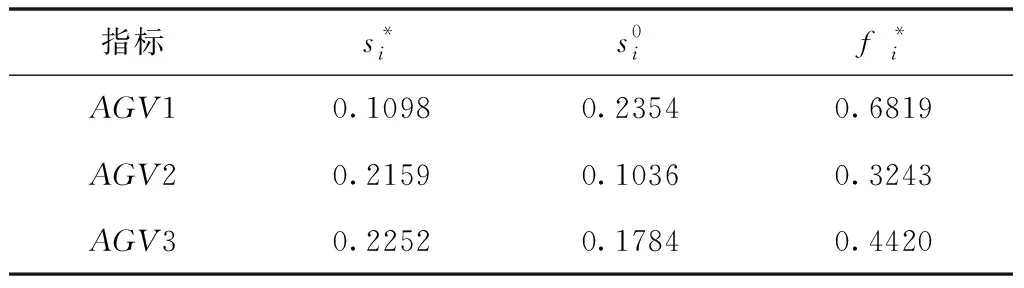
表4 各属性距离值及评价值

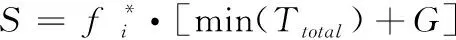
(11)
3 模拟退火遗传算法
3.1 模拟退火算法
模拟退火算法(SimulatedAnnealing,SA)[14]的基本原理如下。相关研究证明当物质进行退火的时时候,高温下分子的活跃度高,自由运动熵增大,以致重新随机排列。一段时间过后开始降低温度,分子慢慢脱离不稳定状况,利用概率的多变性可以在所有随机解空间中找到全局最优解。从理论上来说,在整个算法流程中,最高温度足够高且合理且降温时间充足,降温缓慢,模拟退火算法能以接近100%的概率找到最优解。
3.2 融合模拟退火算法和遗传算法
模拟退火遗传算法(SA&GA)[15]是将模拟退火算法和遗传算法相结合的一种优化选择算法。它综合了模拟退火的全局搜索能力和遗传算法的局部搜索能力,提高了算法的精确性。本文实现模拟退火遗传算法主要分为两个部分,第一个部分利用遗传算法对种群进行编码,在适应度函数的基础上进行选择、交叉和变异操作,得到新的种群。第二部分在新种群的基础上,用Metropolis算法来确定种群状态变化,直至达到稳定。算法的执行过程如图4所示。

图4 混合模拟退火遗传算法流程图
3.2.1 编码
定义染色体编码是解决遗传算法问题的第一步,根据本文实际场景,本文采取比较直观的无起点自然数编码,以工装编号为基因,按照AGV加工顺序组成染色体。假设一共3台AGV,AGV的加工路线如下:
AGV1:3-5-8
AGV2:2-4-1-6
AGV3:7-9
将3台AGV路线接连起来即为染色体编码:358241679。每一个数字代表工装编号,以此类题,直至加工完所有工装。
3.2.2 适应度函数
遗传算法对适应度函数的评价是进行选择操作的依据,根据本文实际场景,模糊函数已由理想解法求出,见式(11),本文以最小化时间为目标,适应度函数如式(12)
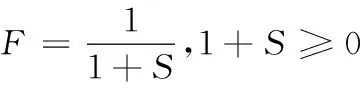
(12)
3.2.3 选择算子
本文选择算子的方式为计算适应度比例的方式。先计出单个个体的适应值占总群总适应度的比例,也就是单个个体被选中的概率。选择过程以“物竞天择”的思想作为选择依据。对于单个个体i,其被选中的概率如式(13)所示
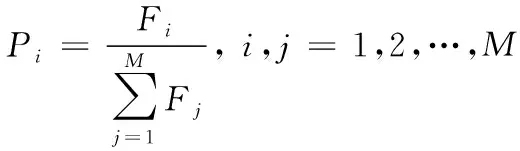
(13)
3.2.4 交叉算子
交叉就是重组两个父辈部分基因片段,以此增加基因的多样性。运用次序交叉的方式进行交叉操作,以工装相对次序为例,这种交叉方式在构造算子时会保存另一个父辈中基因的部分相对次序。
3.2.5 变异算子
遗传算法中发挥主要遗传作用的是交叉算子,变异算子辅助遗传,主要目的是维持种群多样性,产生少量变异个体。本文选取反转变异的方法,在基因片段随机选择两断点,将两断点间的基因片段互换:
未变异:F1=(721|3489|56)
变异后:G1=(721|9843|56)
3.2.6 模拟退火算子
遗传算法得到不同的个体之后,对个体编码进行解码的操作。该种群的最大适应度函数值为Fmax,最小适应度函数值为Fmin。
-ΔF=Fmax-Fmin
(14)

(15)
式(15)中,t0是初始温度;p0为接受劣解的概率,(0

(16)
根据模拟退火算法的收敛速度和优化性能,算法的终止条件即为遗传算法最大进化次数。实际操作中,当进化代数过大,则认为模拟退火算法温度足够低,可以终止算法。
4 实验结果分析
3台重载AGV,编号为AGV1、AGV2和AGV3;8个工装,编号依次从1至8;行驶速度v=0.25m/s;由于工装加工时间均相同,计算过程中均忽略加工时间;AGV当前电量,铆钉数量的权重分别为:0.6和0.4;AGV当前状态如表5所示,工装之间的距离如表6所示。

表5 AGV当前状态

表6 各个工装之间距离
本文采取的算法相关参数为:初始种群个数为100个;进化代数为200;交叉概率为pc=0.85;变异概率为pm=0.15;退火系统中劣解的概率p0=0.95;衰减系数α=0.85。分别利用实验和仿真对传统遗传算法和模拟退火遗传算法进行比较,以及使用了理想解法的优化算法和未使用理想解法的优化算法进行计较。通过Visual Studio 2017设计出调度系统,其主页如图5所示,部分运行日志如图6所示。
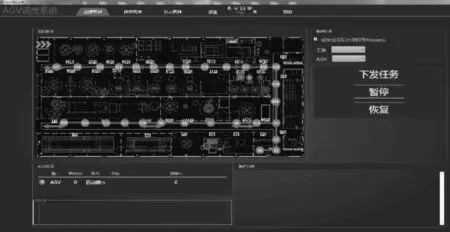
图5 调度系统主页

图6 运行日志
通过试验和MATLAB仿真得到最优路径分别为:
传统遗传算法最优解:
3-8-7,2-5, 1-4-6
未使用理想解法的模拟退火遗传算法:
1-2,3-7-8,4-6-5
基于理想解法的模拟退火遗传算法:
1-2-6, 4-5, 3-8-7
表7为试验和仿真结果,由于AGV2的铆钉数量缺乏,采用了理想解法的调度策略都使AGV2尽量少的进行加工,未采用理想解法的调度策略在铆钉将要使用完的时候需要进行铆钉补充,花费了一定时间,降低系统效率,而且采用了理想解法的算法计算时间更短,有效提高了系统效率和鲁棒性。

表7 不同算法条件下试验和仿真结果
本文提出的算法实际实验时间比基于理想解法的遗传算法时间减少11.2%,计算时间比模拟退火遗传算法所需时间减少18.6%。可以看出模拟退火遗传算法比传统遗传算法具有更好的全局最优解查找能力,更好的避免了遗传算法局部最优解问题。

图7 遗传算法(GA)和模拟退火遗传算法(SA&GA)优化过程
5 结论
针对重载AGV的调度问题,本文以AGV当前电量和铆钉数量为评价指标,利用理想解法建立评价函数,此种方法更能体现实时性,更符合实际生产需求。自适应函数以最小化钻铆机器人调度时间为依据,然后实现多AGV对多个工位的合理调度,在理想解法生成的自适应函数基础上,利用遗传算法对基因进行选择、交叉和变异操作,最后再利用模拟退火算法对新种群进行退火操作,使得遗传算法的解具有更高的全局性,使得算法更精确完善,已达到航空航天装配的高精度需求。
相较于不使用理想解法,本文提出的基于理想解法的模拟退火遗传算法能针对具体场景和具体要求得到最佳的调度策略,实际调度时间更短,而且降低计算量,提高了调度系统的想以速度,增强了系统的鲁棒性,可以达到航空航天加工装配要求。
将理想解法计算得到的适应度函数带入遗传算法中更具有实际意义,在理论对模拟退火遗传算法的每个流程都给出了细致的解答。融合了模拟退火算法的遗传算法的选择全局最优解的能力也有所提升。根据实验和仿真结果,本文提出的混合优化算法能对多AGV的调度系统设计具有一定参考和实用价值。
