“基本型”视角下例谈几何问题解题思路的分析与探索
2022-06-14201306上海市临港实验中学
201306 上海市临港实验中学 王 辉
“和点、线段、弧甚至三角形(这些可称为‘基本元’)不同,在几何问题的分析中,组成一个几何问题图形中最简单、最重要、最基本的但又是具有特定性质的图形称为基本图形”[1].我们平时所说的平行A字型(如图1所示)、平行8字型(如图2所示)、交错A字型(如图3所示)、交错8字型(如图4所示)等都是基本图形.为使表述更简洁,不妨将它们称为“基本型”.笔者以偶然得到的一个命题的解法为例,以“基本型”为视角,对其解题思路展开探究.

图1图2

图3图4
在笔者的一次听课中,有位教师在课堂上给出了这样一道例题.
如图5,已知DE∥BC,AO,DF相交于点C,∠EAB=∠BCF.
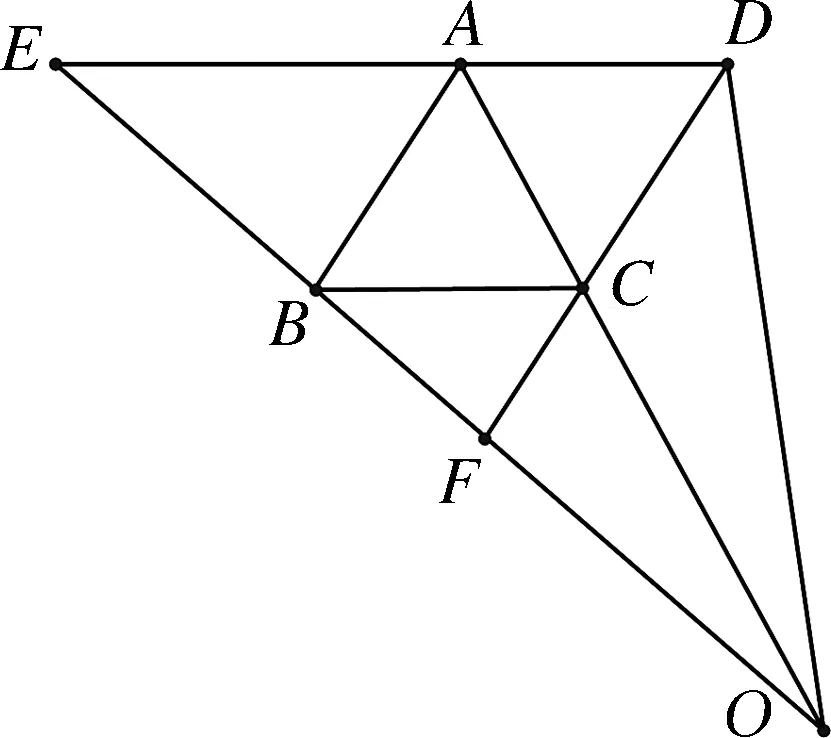
图5
(1)求证:四边形ABCD是平行四边形.
(2)若∠OBC=∠FDO,OB=OD.求证:四边形ABCD是菱形.
笔者发现小问(2)有多余的条件.经课后询问执教教师得知,这是为了降低难度而改编的题目.在执教教师的帮助下笔者得到了原题(下文将呈现),尝试将小问(2)中的∠OBC=∠FDO条件去掉,很容易得到结论.当尝试去掉条件OB=OD时,笔者对是否可以证明得到结论产生了疑惑,故尝试将题目改写成如下命题.
已知:如图6-1,在△ABC中,∠ABE=∠ACE,BD=DC,那么AB=AC.

图6-1
由于题中的两个条件互相独立,彼此不易建立直接的关系,这道题便成了一道难题.为此,用同一法进行证明,将问题转化为熟悉的“基本型”.如图6-2,过B作BG⊥AD交于F并倍长至G,联结AG,CG,EG,通过中位线定理(平行A字型)得出AF∥CG,通过对称全等得到∠ABE=∠AGE=∠ACE.由C,G在AE同侧,依据四点共圆判定定理可证C,G在同一个圆上.如图6-3,由于直线CG和圆只有两个交点G和G′,显然G′不成立,从而可证点C和G重合,从而证得AB=AC.

图6-2 图6-3
采用此法是因为等角的条件不太好直接使用,便通过轴对称的方法变化角的位置,通过交轨法确定两点重合,其本质是构造重合的图形.
这是此命题的一种证法,而这种同一法的证明只是教师的思考,是否适合学生的实际还有待探索.为了解学生的真实思考,得到更多的探寻思路,发挥学生的奇思妙想,笔者将此题作为长作业发布在班级微信群中.意想不到的是,学生反馈的证明个个是精品,令笔者喜出望外.在此呈现甲、乙、丙、丁四位学生的证法,他们都是独立完成证明的,其思路各有不同,亦有联系,从中细品别有滋味,回味以启解题之智.
生甲证法:如图7-1,延长BE,CE分别交AC,AB于点G,F,倍长ED至E′,联结BE′,CE′(证明思路如图7-2所示).
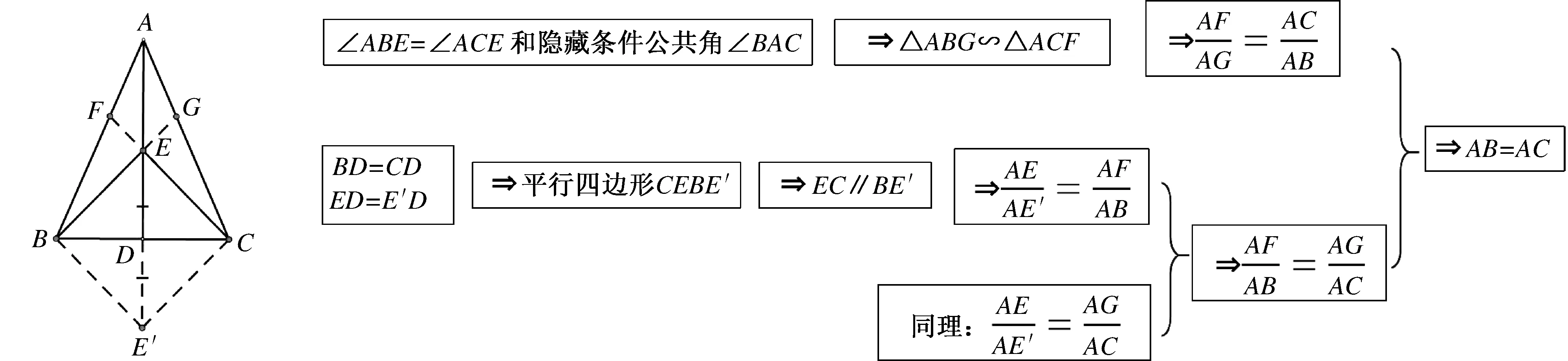
图7-1 图7-2
分析:由角相等联想共角三角形相似,再由相似得出比例线段.由线段的中点联想中心对称,构造平行四边形,得出平行A字型图形,得出比例线段,发现两个共边平行A字型图形,传递比例,最终通过等式性质得以证明.
由此分析得到以下与之相近的证法.
证法1:如图8-1,延长BE,CE分别交AC,AB于点G,F,过D作DH∥CE交AB于H,过D作DI∥BE交AC于I(证明思路如图8-2所示).

图8-1 图8-2
证法2:如图9-1,延长BE,CE分别交AC,AB于点G,F,过A作KJ∥BC交BE,CE的延长线于J,K(证明思路如图9-2所示).
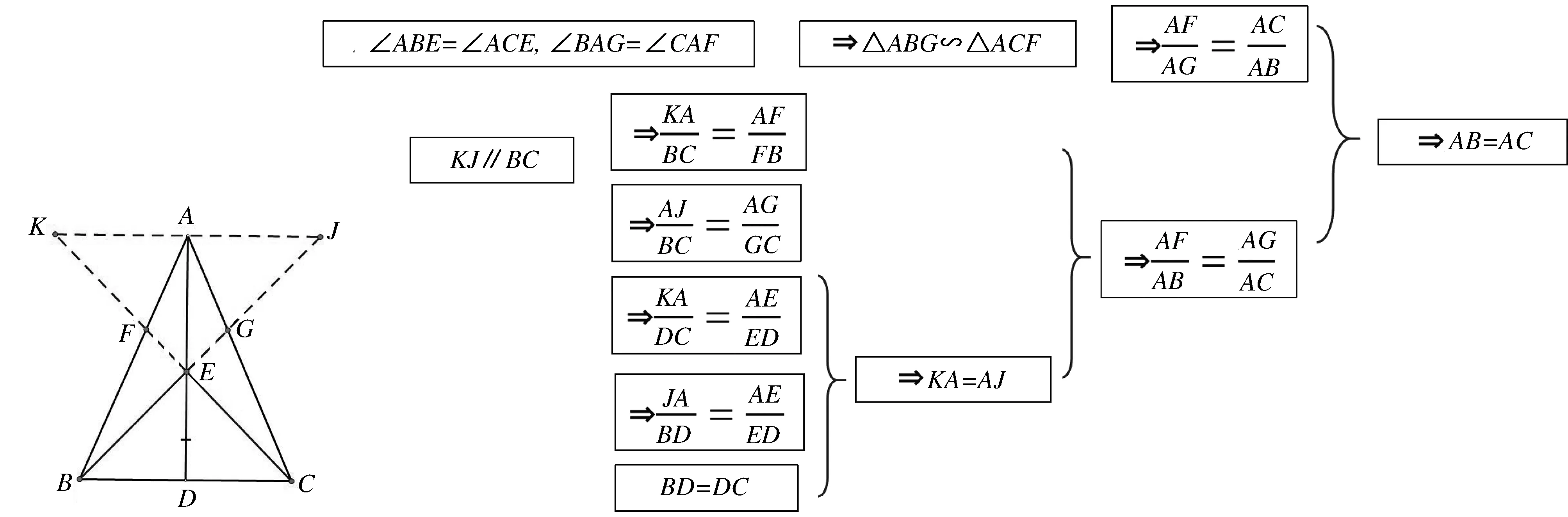
图9-1 图9-2
以上证法集中分析相似三角形、平行A字型、平行8字型等“基本型”,通过角相等和线段中点联想“基本型”,进而从“基本型”中得出比例线段,再建立关系解决问题.

分析:由D是BC的中点联想到三角形的中线,进而联想到三角形的面积被平分,通过等式性质发现△ABE和△ACE面积的恒等,再由角相等联想到三角形面积的正弦公式,结合三角形的边角不等关系推出矛盾,进而得出结论正确.(正弦面积公式和三角形边角不等关系为学生自学掌握的,得出此法实属不易)
生丙证法:如图10-1,分别过A,E作AF∥BE,EF∥AB,交点为F,且EF交AC于H,联结CF,BF交AD于G(证明思路如图10-2所示).
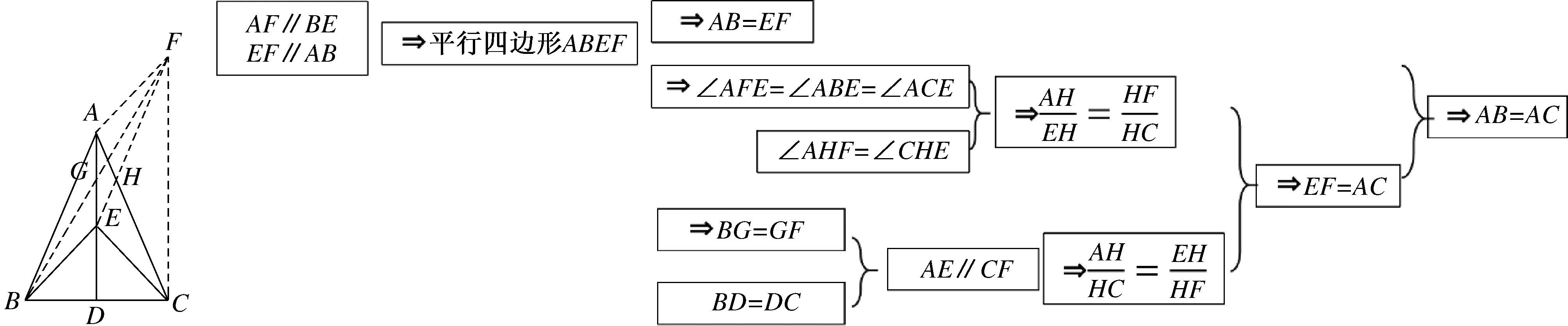
图10-1 图10-2
分析:此处并没有从条件直接切入“基本型”,而是通过运动改变角的位置,进而构成了熟悉的交错8字型和平行8字型图形,最终得以解决问题.
生丁证法:如图11-1,过E作FG∥BC交AB于F,交AC于G,过E作EH∥AC交BC于H,联结FH交BE于Q(证明思路如图11-2所示).

图11-1 图11-2
分析:此证法本质与生丙的证法相仿,意在将角通过运动或基本图形(平行四边形、等腰梯形等)的性质建立关系,组成新的平行8字型和交错8字型共存的“基本型”,最终解法与上例类似.
以上的证法看似各有不同,深挖条件以构造、固定条件求冲突、运动条件组新图,其实质都是利用条件联想“基本型”,再由“基本型”的性质联想相关结论,综合几个“基本型”得到结论,找到证题思路.条件是撬动“基本型”的支点,“基本型”是产生条件的载体,观察“基本型”之间的关系,联想条件的联系,简化冗长思维,聚焦基本图形,融通相互关联,“基本型”的视角是提升分析、解决几何问题能力的有效途径.
再回到上文提到的执教教师修改前的原题.
如图12-1,已知DE∥BC,AO,DF交于点C,∠EAB=∠BCF.

图12-1
(1)求证:AB∥DF.
(2)求证:OB2=OE·OF.
(3)联结OD,若∠OBC=∠ODC,求证:四边形ABCD为菱形.
分析:小问(1)由条件直接联想到平行四边形(证明思路如图12-2所示).
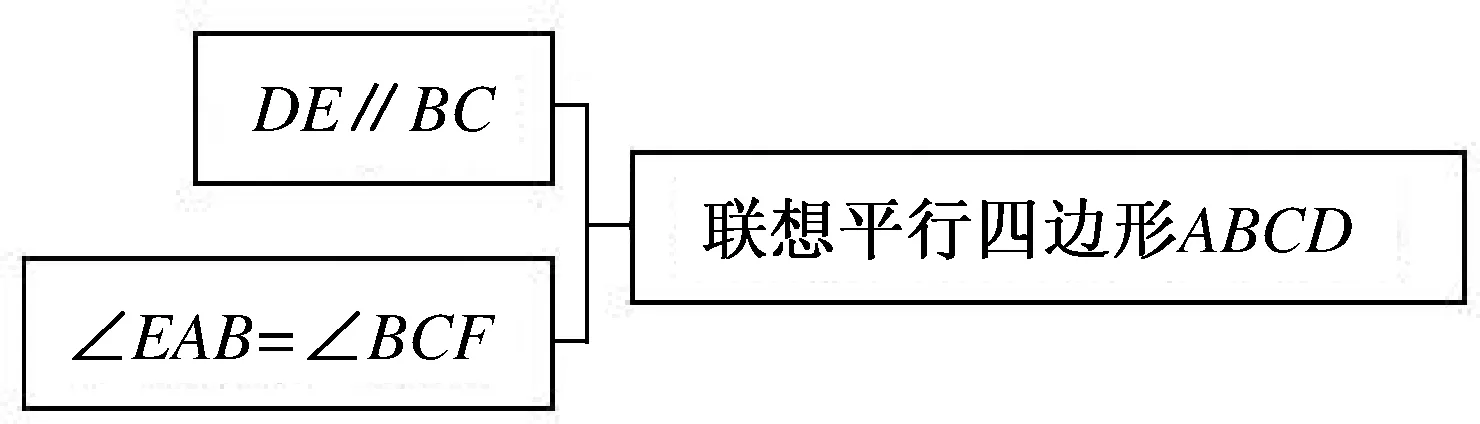
图12-2
小问(2)由平行四边形的两组对边的位置关系,结合本题图形联想到平行A字型,且由结论化为比例线段,设法找到合适的平行A字型,让两个平行A字型建立共边位置关系就能解决问题.这一问题提示以“基本型”为抓手,通过条件的正向联想和结论的逆向联想建立“型”与“型”之间的联系,更好地聚焦和简化思考过程(证明思路如图12-3所示).
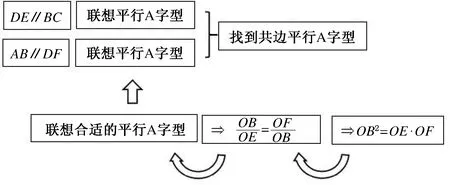
图12-3
小问(3)由小问(2)的结论容易联想到OD2=OE·OF,通过角的关系挖掘很容易联想到共角共边型(如图12-4所示),综合易证得到OB=OD,接下来的证明就是一马平川了(证明思路如图12-5所示).
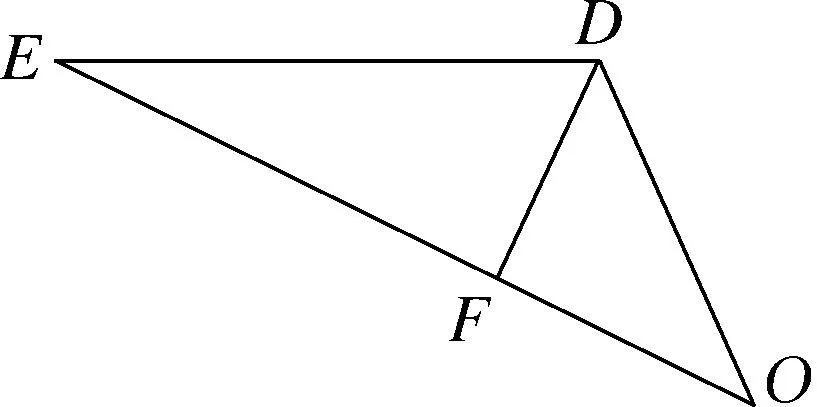
图12-4

图12-5
由前面的分析,笔者将一些几何问题的解决过程简化为以下的思考路径图示(如图13所示).

图13
人们思考问题时总是从条件或结论出发.从条件出发可以联想建立什么样的“基本型”,从结论出发对需要证的结论进行转化或拆分,可以预设需要什么样的“基本型”,在“型”与“型”之间,通过图形或产生的结论的联系解决问题.
基本图形分析法就是在几何学科中,根据问题的条件和结论,分析并找到组成这个几何问题的一个或若干个基本图形,再应用这些基本图形的性质,使问题得到解决的几何方法.[2]
本次尝试虽是一次偶然的活动,但笔者对学生蕴藏的无限潜能感到惊喜,从中获得以下启发.
1.“基本型”的几何分析简化了学生繁复冗长的解题思路,将原本的条件升华为基本图形及基本图形之间的关系.
2.对于单个条件无从下手时,可以寻找隐性条件或改变其几何位置将其转化为“基本型”,为突破难点开辟道路.
3.在综合的问题中通过“基本型”的性质引出有用的信息建立关系,往往这些信息存在于“基本型”的组合中,需要关注基本图形中的共角、共线等.
4.类似于判定定理和性质定理,在平时教学中应注重条件到“基本型”、“基本型”到结论的知识积累,这是学生遇到问题能够及时反应的有效手段.
5.“基本型”学习是一个累进的过程,如最初学习的只是基本的平行A字型、平行8字型等,之后可学习基本图形的组合型(如生丙和生丁最终都利用的平行8字型、交错8字型共存的“基本型”).
及时的反思小结如同在收获的路上为装满果实的袋子扎上袋口,对保持学习的成果起到事半功倍的作用.在笔者给出的命题的基础上,生乙有了新的想法,他提出了以下命题.
已知:如图14,在△ABC中,∠ABE =∠ACE,AD⊥BC,那么AB = AC.

图14
其实这个命题是假命题,但能够给予学生“学无止境,越思考越聪明”的启示.
