单元教学视野下的学习活动设计<br/>——以概率单元的知识构建活动为例

单元教学视野下的学习活动设计
——以概率单元的知识构建活动为例

2022-06-14200433复旦大学附属中学肖恩利

中学数学 2022年3期

200433 复旦大学附属中学肖恩利

在利用沪教版普通高中教科书《数学》(新教材)实施教学的过程中，围绕单元教学设计，特别是在新知构建的过程中，怎样开展学生学习活动设计？笔者以筹备复旦附中张建国老师的展示课“事件的关系和运算”为契机，在概率单元的教材内容、教学方法和活动设计等方面进行深入学习和探讨，形成以下思考.

一、始于困惑和问题

困惑1新教材在讲授概率之前并没有给出计数的内容，这与之前的处理方式有较大区别，怎样理解这种变化？教师怎样教？学生怎样学？

困惑2新教材中，“古典概率模型” “古典概率” “经典概率”和“几何概率”等名词交替出现.怎样理解“古典概率模型”在本单元中的作用？

困惑3新教材用两节的篇幅介绍了“等可能性”，并且在第98页提到“在古典概率模型中，随着观察角度的不同，并非所有的样本空间都是等可能的……虽然取什么样本空间不影响所考察的随机事件的概率，但只有选取等可能的样本，才能使得事件的概率如定义所示，等于事件元素个数与样本空间元素个数之比，进而使有关计算变得简单”，那么，“等可能性”的意义是什么？

困惑4怎样理解教材第103页提到的“概率最本质的性质就是可加性”？

困惑5从知识体系来看，必修一教材以函数为中心，必修二以几何与代数为中心，那么必修三的中心是什么？

问题1从正整数集中随机地取一个数，那么这个数是1的“概率”是多少？

李继根教授所著《概率与统计》一书中提到了问题2的三种解法.

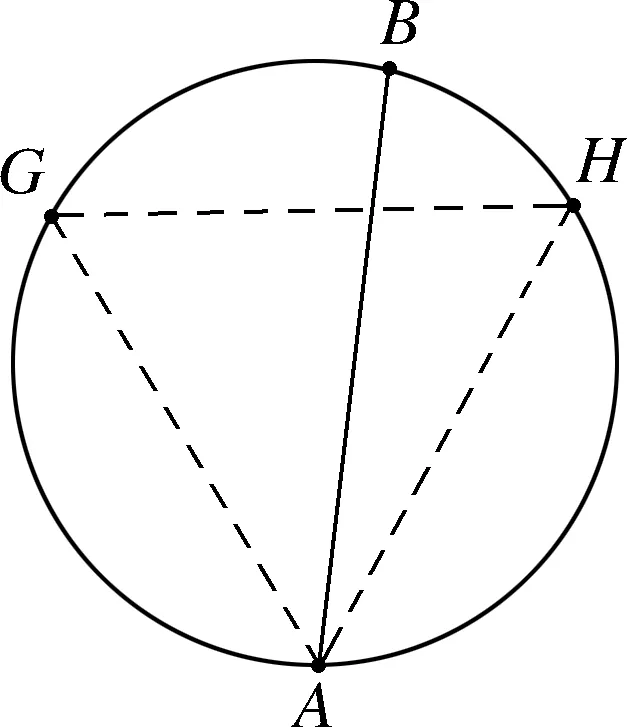
图1

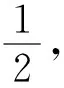
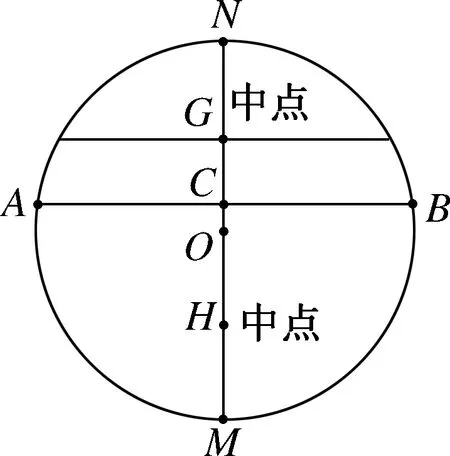
图2

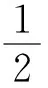
图3

二、教师的“研学”

为解决这些困惑和问题，笔者查阅了《普通高中数学课程标准(2017年版2020年修订)》《普通高中数学课程标准(2017年版)解读》，这些文件解决了“教什么”的问题，但是具体的“怎么教”“为什么这么教”等问题则需要通过教师的实践才能解决.经过认真学习编写者的培训内容，仔细研读新教材和一些概率论教材，困惑2的答案浮出水面.新教材中的概率内容是建立在集合论基础上的公理化体系，即概率是事件域上的广义函数，但囿于高中数学中“函数”的定义，教材没有以明确的公理形式呈现概率定义，而是借助古典概率中的古典概率模型，形成了概率的四条性质(如图4所示).因此，“古典概率模型”在本教材中起到了“拐杖”的作用，教与学都要借助于这个“拐杖”逐步展开.

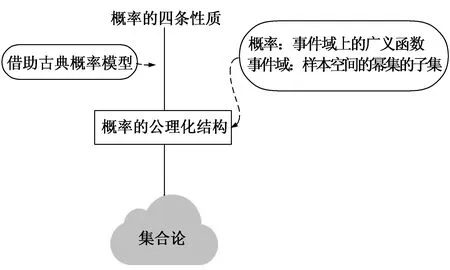
图4

因此，困惑1和困惑5也迎刃而解.

对困惑1的认识：传统的计数内容(乘法原理、加法原理、排列组合等)中有较多难点，如果仍然以这部分内容作为教授概率的开端，会冲淡新教材中“公理化”的主题，不利于帮助学生体会公理化思想的价值和意义.因此，教师要在充分理解概率公理化结构的基础上，通过对学生已有认知基础的“经典概率”进行深度挖掘，引导学生认识到集合在描述随机事件、刻画随机事件的概率中的功能，认识对“经典概率”进行数学化和科学化的必要性，了解公理化的意义(如图5所示).这就是张建国老师在设计本节课时的出发点.相应地，教师可以设计丰富多彩的学习活动，既可以围绕“经典概率”中的著名问题展开讨论，如教材中提到的“赌徒分奖金问题”等，也可以围绕概率的发展史进行学习.张建国老师的教学设计中充分加入了这方面的思考，设计了课后学习活动内容，要求学生查阅概率的定义发展过程中与公理化形成有关的资料，从中体验和感悟公理化体系的思想.

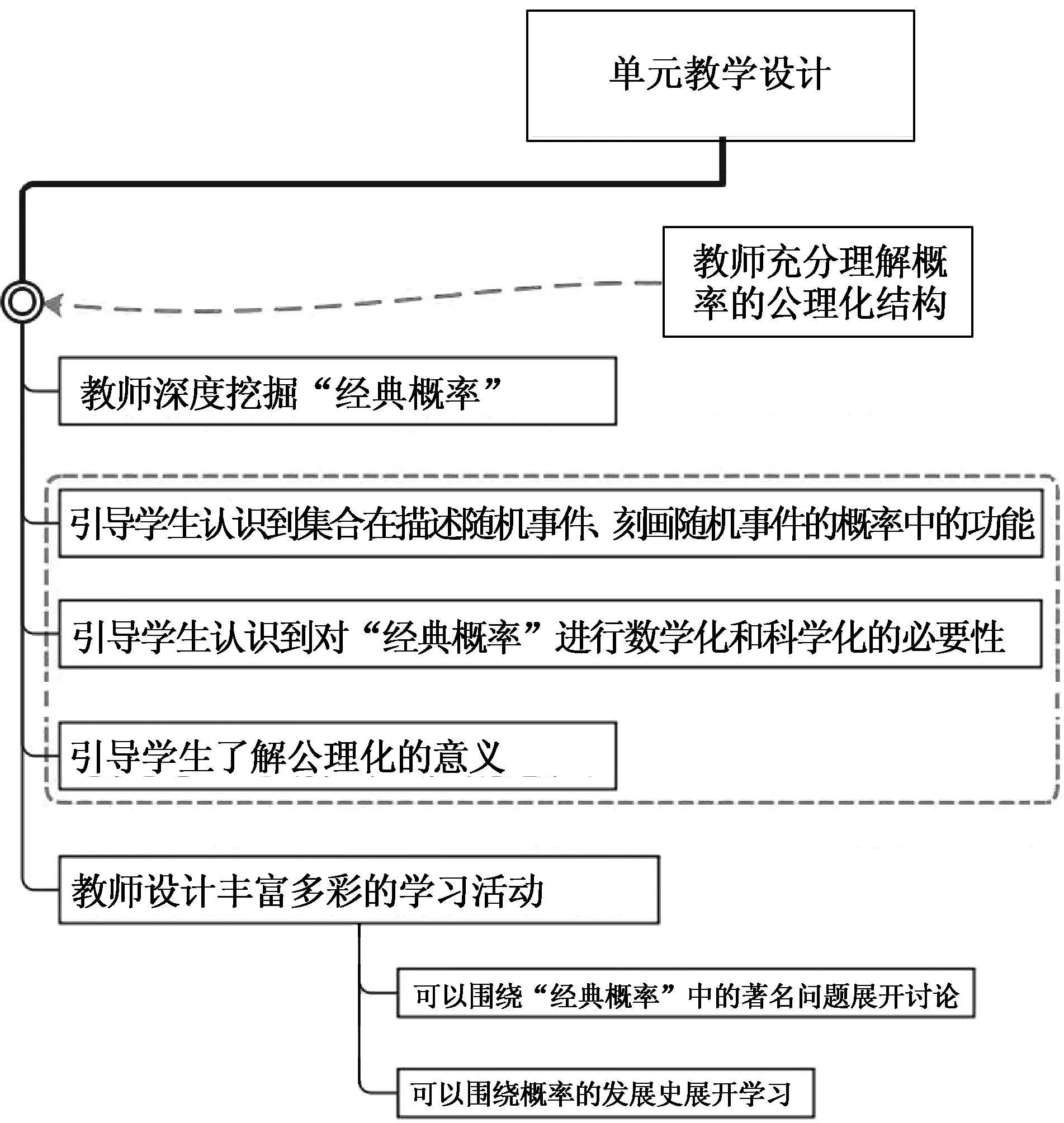
图5

对困惑5的认识：课标中，除了选修课程专设的“逻辑推理初步”中有明确的“公理化思想”内容之外，仅在“学业质量水平划分”和“数学学科核心素养的水平划分”中提及了“公理化思想”.反观中学数学中，体现“公理化思想”的内容包括整数、集合、平面几何与立体几何、概率，与它们相对应的公理体系分别是皮亚诺算术公理体系、策梅洛—弗兰克尔集合论公理体系、欧几里得几何公理体系(以及希尔伯特几何公理体系)、柯尔莫哥洛夫概率论公理体系(如图6所示).这也为认识和理解新教材必修三的教学内容提供了一个角度.当然，限于中学数学的知识范畴，除了平面几何与立体几何因其直观性可以给出明确的、经过适当改造的公理内容之外，其他三方面的内容并不适合直接将公理内容呈现给学生，例如概率的公理化结构必须借助古典概率模型渗透到学生的知识结构中.

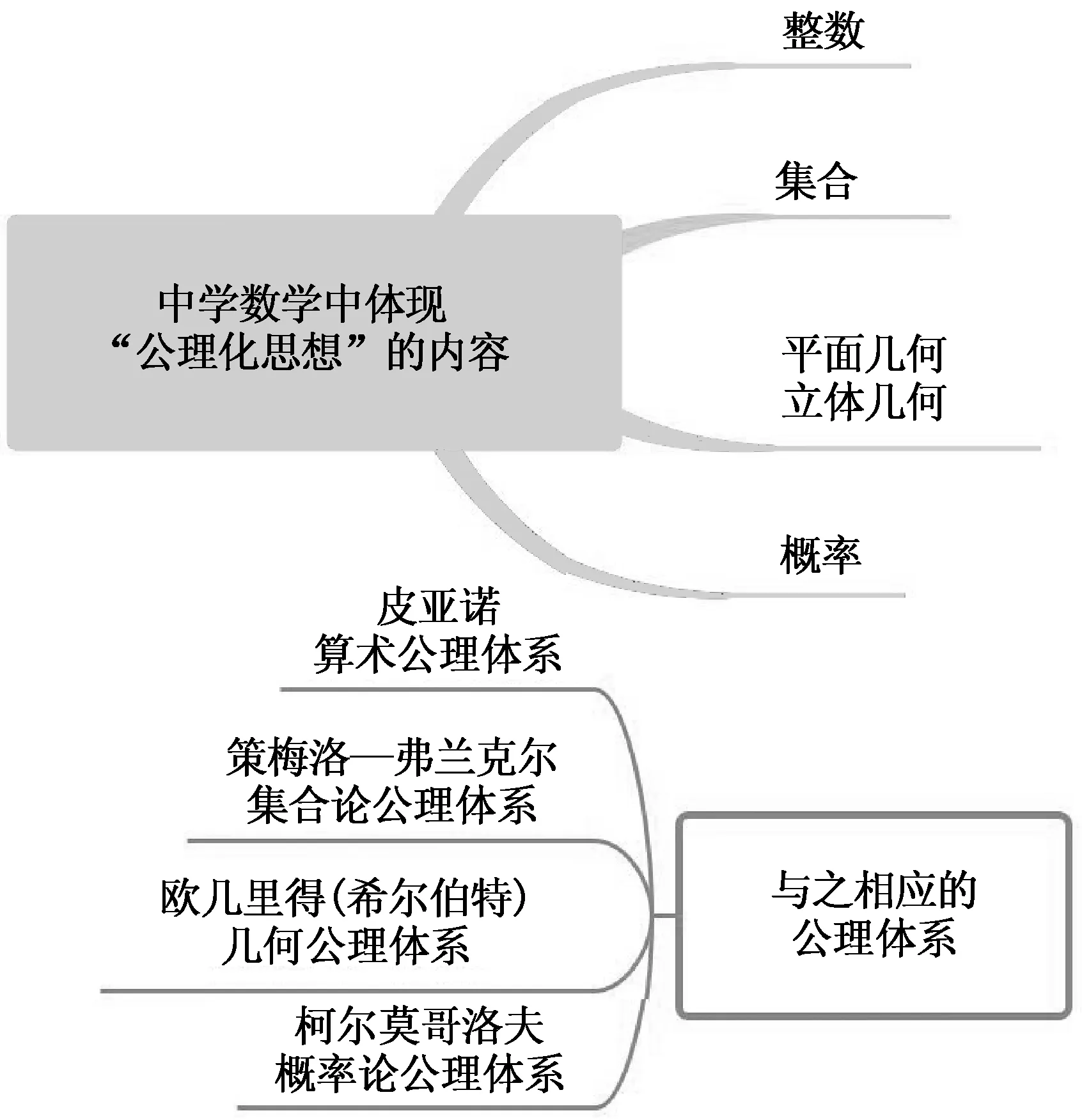
图6

从以上分析中可以看到，新教材的概率单元对教师的知识结构、教学方法甚至教育理念都提出了比较高的要求.从知识结构来看，教师不仅要有扎实的数学功底，也要对中学数学中涉及的数学历史、数学文化有充分了解，这样在设计相关内容的教学过程中，才能做到“心中有数，脉络清晰”.从教学方法看，教师要对学生的认知能力、认知习惯有细致的把握，对单元内容进行充分、深度学习，从单元整体、知识整体进行完善的教学设计，设计丰富的学习活动，引导学生思考，提升数学素养和数学意识.从教育理念看，教师也应处于不断的学习中，把自身对数学的“学习活动”转化为学生的“学习活动”.

三、对教材和公理化的再认识

从新教材的概率内容看，新教材实际上给出了三种形式的概率定义，即拉普拉斯的古典定义、米泽斯(基于大数定律)的统计定义和柯尔莫哥洛夫的公理化定义.其中古典定义的核心是“等可能性”，“等可能性”源于人们对未知领域的合理假设，教材以“为什么硬币的两面出现是等可能的”为例阐述了这种思想的来源.历史上，拉普拉斯在《概率的分析理论》中，将“平等”这个理念数学化为“等可能性”，他指出“当没有什么使我们相信一个事件比其他任何事件更应该发生时，这些事件对我们来说就是等可能的”.而公理化定义的核心是“可加性”，也就是说公理化定义不再拘泥于学生熟悉的“等可能性”，正如教材所说，“作为度量某事件发生可能性大小的量，概率最本质的性质就是可加性，它在计算概率时非常重要”.在古典概率模型中，“可加性”的实质是“有限可加性”，而对于含有无穷多个基本事件的概率模型(如几何概率)，“可加性”的实质是“可列可加性”.

从以上的认识来看问题1和问题2，就会得到一些有趣的现象.

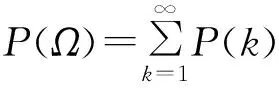
问题2提到的贝特朗悖论更让人疑惑，根据似乎是显然的“等可能性”，竟然可以得到同一个问题的多个不同的答案，关键是这些答案似乎都是正确的.产生这一现象的原因又是什么呢？

实际上，上述两个问题中，看似反常的现象产生的原因就在于对 “随机”“等可能”等术语的使用，即仅仅依靠直觉，没有明确地指出是在哪个样本空间上的“随机”，也没有验证“等可能性”是否符合概率论的公理化体系.作为一门成熟的数学学科，概率论不能够仅仅依靠直觉，更需要一种简明的数学结构使得一些现实的与概率有关的现象能够被推导和证明，因此概率公理化体系的建立是一个数学史上里程碑式的进步.

在最开始进行教学设计的过程中，复旦附中数学备课组内有教师认为从教材内容来看，“事件的关系和运算”一节的内容似乎有些单薄，可以考虑将这一节与下一节“可加性”合并为一节课.在备课组充分讨论的基础上，这一方案被否定了，原因在于这两节课的主题是完全不同的.“事件的关系和运算”的主题是利用集合语言描述随机事件，通过古典概率模型体会这种描述方式的科学性和严谨性；而“可加性”的主题是凸显概率的度量特征，通过古典概率模型研究概率的运算性质.如果把“可加性”比喻为要到达的“目的地”的话，“事件的关系和运算”就是通往这个“目的地”的必经“桥梁”.到达“目的地”意味着公理化定义的完全形成；而“桥梁”的意义在于它可以到达多个“目的地”.张建国老师在他的教学设计中设置了一项课后的学习活动，要求学生通过查找资料，研究是否可以通过事件的运算来理解集合的其他运算，也正是基于这样的考虑.