近场水下爆炸气泡脉动及水射流的实验与数值模拟研究*

文彦博，胡亮亮，秦 健，张延泽，王金相，刘亮涛，黄瑞源

（1. 南京理工大学瞬态物理国家重点实验室，江苏 南京 210094；2. 福州大学土木工程学院，福建 福州 350116；3. 上海宇航系统工程研究所，上海 201109；4. 海军研究院，北京 100161）

随着水下精确制导武器的发展，舰船遭受近场水下爆炸攻击的概率越来越大。近场水下爆炸能对舰船等海上作战平台造成毁灭性的打击，因此，研究近场水下爆炸对现代海洋战争有着重要的战略意义。近场水下爆炸载荷主要可分为冲击波阶段及气泡射流阶段，20 世纪80 年代以前，水下爆炸相关研究主要集中于冲击波对结构造成的破坏。从20 世纪80 年代开始，人们逐渐意识到气泡脉动对结构的损伤可能不亚于冲击波，进行了大量的水下爆炸实验，得到了广泛使用的水下爆炸经验公式。一般认为，气泡脉动带来的滞后流及气泡脉动压力能造成舰船的总体毁伤，气泡收缩的最后阶段，气泡坍塌继而形成的高速水射流则能严重毁伤舰船局部。近年来，水下爆炸中的水射流现象及其载荷特性已成为关注的热点。

在开展水下爆炸气泡与边界相互作用的研究时，因炸药爆炸具有一定的危险性且实验成本较高，多采用电火花或激光生成气泡的方法。但电火花生成的气泡内部为可冷凝的水蒸气，而炸药水下爆炸生成的气泡中心为高温高压气体、外部为水蒸气，二者存在物理本质上的差异，所以有必要开展炸药水下爆炸实验。Klaseboer 等通过在水池中进行水下爆炸系列实验，拍摄了完整的气泡坍塌形成水射流的过程，并基于边界元方法模拟了爆炸气泡与水下弹性结构相互作用的过程。牟金磊等在水箱内开展了水下爆炸系列实验，测得气泡射流阶段的压力时程曲线呈马鞍形，并对Blake 判断准则进行了修正。Gan 等在水箱内开展了简化的细长浮式结构在水下爆炸作用下的实验和数值模拟研究，并采用CEL 方法对第1 次气泡脉动期间气泡与水面结构作用的全过程开展了数值模拟。Cui 等在水箱内开展了小当量炸药在不同边界条件下的水下爆炸气泡特性实验研究，得到了不同边界条件下气泡的形态及压力特性。然而，目前的研究主要集中在近场水下爆炸气泡水射流在不同边界条件下的演化过程和压力特性，对水射流速度和时间特性的研究不够深入。

舰船遭遇近场水下爆炸攻击时，爆心的位置多为舰底或舷侧。本文中，为了研究底部爆炸时气泡水射流阶段的载荷特性，首先开展TNT 当量2.5 g 的炸药在固支方板底部不同爆距下起爆的水下爆炸系列实验，通过高速摄像拍摄不同爆距下气泡与钢板相互作用形成水射流的图像。实验现象表明，固支方板底部水下爆炸形成的射流可分为吸附式射流和非吸附式射流。接着，基于ABAQUS 软件，采用CEL 方法开展了数值模拟研究，先验证数值模拟的准确性，再通过系列数值模拟探究吸附式射流向非吸附式射流转化的临界点，同时给出临界点附近爆距下的气泡演化过程。最后，以速度云图形式给出不同爆距下水射流形成的过程，并讨论爆距对水射流开始形成、达到最大速度和击中固支方板时速度特性和时间特性的影响。可为利用气泡射流现象对舰船等典型海上目标实施毁伤打击提供参考。

1 固支方板底部水下爆炸实验

1.1 实验方案

固支方板底部水下爆炸实验在江苏永丰机械有限责任公司的2 m×2 m×2.2 m 水箱中进行。图1 为实验系统，主要由敞口水箱、高速摄像机、水下压力测试系统组成。水下压力测试系统由NI 公司的PXle-4480 数据采集卡、PXle-1082 机箱、PXle-8880 控制器以及PCB 公司的138A06 水下压力传感器组成，测试系统的采样率为2×10s。高速摄像机帧频为3 200 s。炸药为TNT，药量为2.5 g。图2 为固支方板实物，固支钢板尺寸为70 cm×70 cm×1 cm，材料为Q235 钢，钢板的四周焊上挡水板，挡水板尺寸为70 cm×10 cm×1 cm，钢板的四角焊上支架，支架材料为直径30 mm 的钢棒，底座为200 mm×200 mm×8 mm的钢板，可使钢板在冲击波作用下保持稳定。在距炸药70.0 cm、距水面20.0 cm 处布置水下压力传感器，并在传感器正下方悬挂配重为1.5 kg 的秤砣。炸药由钢丝固定在钢板中心的正下方，水面与水箱底部的距离为1.2 m，没过钢板。

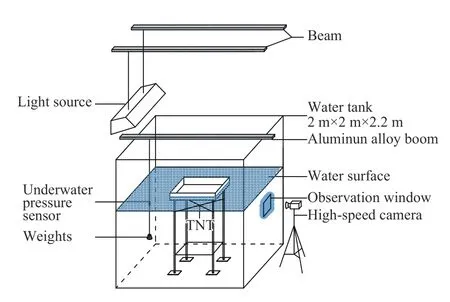
图1 实验系统Fig. 1 The experimental system

图2 固支方板Fig. 2 A clamped square plate

为探究炸药到靶板的距离对气泡射流现象的影响，根据汪斌等的实验，本文中设计炸药到钢板的距离分别为15.0、17.5、20.0 和28.0 cm，定义距离参数γ，并有经验公式：

式中：为气泡最大半径的理论值（m），为炸药质量（kg），为炸药深度（m）。

本文中对应的距离参数γ 分别为0.684、0.798、0.913 和1.282。

1.2 实验结果

1.2.1 水下传感器测试结果

在距爆心70.0 cm、距水面20.0 cm 处布置了水下压力传感器，图3 为水下传感器记录的实验1 压力曲线，其中冲击波压力峰值为7.64 MPa，气泡脉动压力峰值出现在38.39 ms，其值为1.77 MPa。对自由场中水下爆炸冲击波的传递，Cole通过对大量实验数据的整理，总结了水下爆炸冲击波的经验公式，并得到了广泛认可，Zamyshlyayev 等在其基础上改进为：

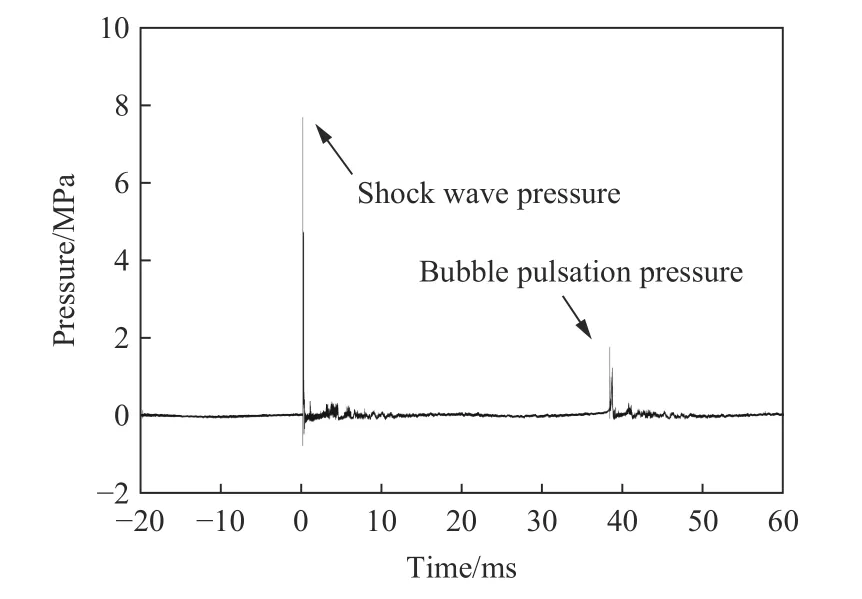
图3 实验1 的压力曲线Fig. 3 The pressure curve in experiment 1

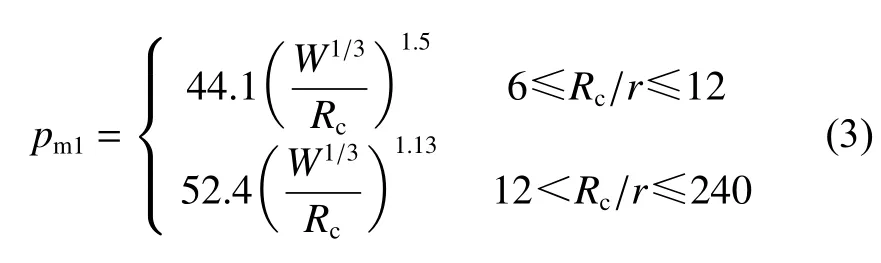
式中：为冲击波超压（MPa），为测点到爆心的距离（m），为药包半径（m）。王高辉等指出，自由边界和平板边界对冲击波传播特性的影响主要集中于入射波峰值之后，对入射波峰值的影响几乎可以忽略不计。因此，可将本文中测得的冲击波峰值压力与经验公式计算结果进行比较。表1 为不同距离参数时水下压力传感器的冲击波峰值压力与2.5 g TNT 水下爆炸经验公式计算结果的比较。可以看出，实验冲击波压力峰值与经验公式计算结果的偏差δ在10% 以内，并且相同距离参数时偏差之间不超过3%。

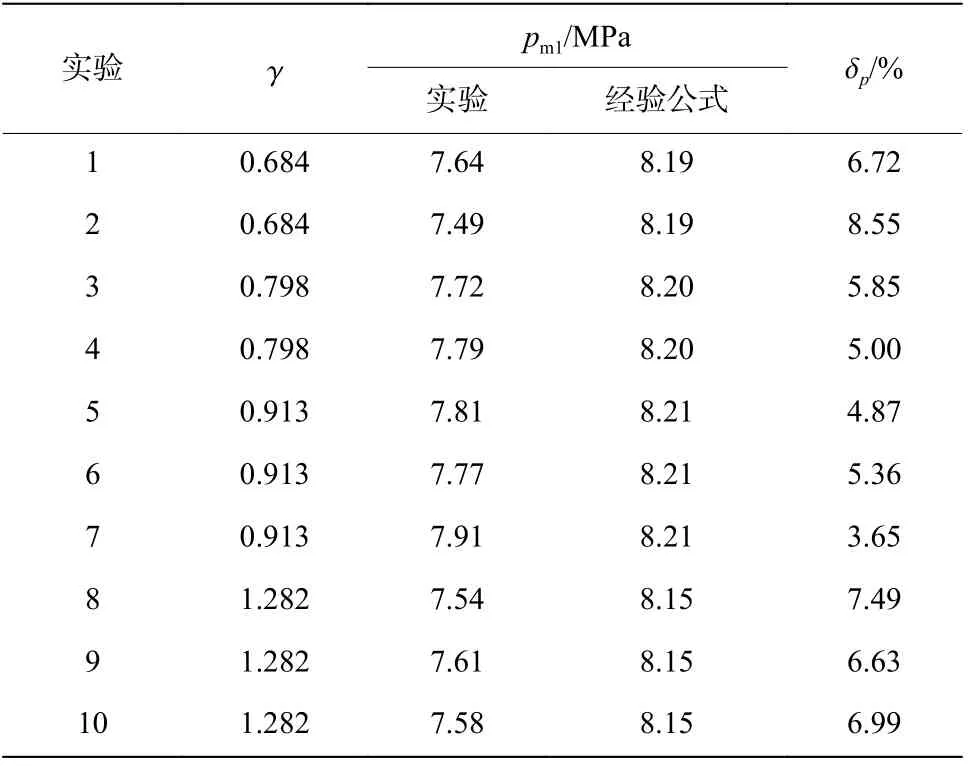
表1 冲击波峰值压力的实验结果和经验公式结果Table 1 Experimental results and empirical formula results of shock wave peak pressures

1.2.2 高速摄像测试结果

图4 为距离参数γ=0.684 时气泡演变过程的高速摄影图像。在0～3.75 ms 时，气泡受到的Bjerknes 力较小，其形状为球形。在3.75～19.06 ms 时，因钢板阻碍了气泡的发展，气泡上半部分明显呈扁平状，下半部分仍保持球状。在气泡收缩阶段，气泡在Bjerknes 力及浮力作用下向上迁移，气泡与钢板发生接触，吸附在钢板上，在25.63 ms 时能明显看到吸附在钢板上的气泡在钢板与水面间形成盘状区域。接着，气泡开始进一步吸附在钢板上，在34.36 ms 时，已吸附在钢板上的气泡呈漏斗形，而未吸附在钢板上的部分仍保持为球形。在38.75 ms 时，气泡完全吸附在钢板上，整体呈漏斗形。由于漏斗形气泡底部曲率半径最小，最容易发生失稳，导致气泡底部发生凹陷并产生向上的射流。在44.69 ms 时，气泡在钢板附近溃散形成气泡群，且在气泡群下方能看到，爆炸残留物在水流的作用下呈放射状指向钢板。

图4 当γ=0.684 时气泡演变过程的实验图像Fig. 4 Experimental images of bubble evolution process when γ=0.684

图5 为γ=0.798 时气泡与钢板作用演化过程，其现象基本与γ=0.684 时的一致。

图5 当γ=0.798 时气泡演变过程的实验图像Fig. 5 Experimental images of bubble evolution process when γ=0.798

图6 为γ=0.913 时气泡与钢板作用演化过程。在0～9.38 ms 时，气泡近似自由膨胀，其形状为球形。在12.19 ms 时，气泡上表面在钢板Bjerknes 力排斥作用下，上半部分呈扁平状。在19.06 ms 时，气泡膨胀过程结束，在浮力及收缩过程中钢板Bjerknes 力吸引作用下，气泡上表面与钢板接触，形成盘状区域，见28.13 ms 时图像。与γ=0.684, 0.798 时不同，当γ=0.913 时，气泡在收缩阶段并未完全吸附在钢板上，而是与钢板间存在一层水层，见γ=0.798 在34.36 ms 时图像。在收缩过程中，气泡上表面位置保持不变，而下表面向上表面靠拢，在39.69 ms 时能看到气泡半径收缩至最小，形成指向钢板的射流。在43.13 ms时，气泡发生溃散，形成小气泡群。

图6 当γ=0.913 时气泡演变过程的实验图像Fig. 6 Experimental images of bubble evolution process when γ=0.913

图7 为γ=1.282 时气泡与钢板作用演化过程。在0～9.38 ms 时，气泡形态受Bjerknes 力影响较弱，其形状为球形。在7.81～19.06 ms 时，随着气泡的膨胀，其上表面与钢板间的距离减小，气泡受钢板的阻力变大，气泡上半部分难以自由膨胀，导致上半部分呈扁平状，下半部分为球形。在气泡收缩阶段(19.06～40.63 ms)，在Bjerknes 力的影响下，气泡恢复球形，同时质心位置发生上移。在第1 次气泡脉动结束后，在40.93 ms 时能看到一束气液混合的高速射流冲向钢板，由相邻两帧高速摄像可以估算射流速度为65 m/s。同时，随着气泡的收缩，能清晰看到爆炸残留物在水流的带动下呈放射状指向钢板，见42.19 ms 时图像。

图7 当γ=1.282 时气泡演变过程的实验图像Fig. 7 Experimental images of bubble evolution process when γ=1.282

气泡脉动周期和气泡最大半径是表征气泡脉动现象的两个主要参数，对TNT 有经验公式：

式中：为第1 次气泡脉动周期（s）。表2 为气泡脉动周期和气泡最大半径的实验值及经验公式计算结果，其中气泡半径的表征方法同文献[22]。气泡脉动周期及气泡最大半径均小于经验公式计算结果。由于固支方板与气泡间的Bjerknes 效应，使气泡坍塌速度加快，导致气泡脉动周期偏小。由于顶部固支方板阻碍了气泡自由膨胀，而经验公式在自由液面的前提下，所以实验测得的气泡最大半径小于经验公式计算结果。

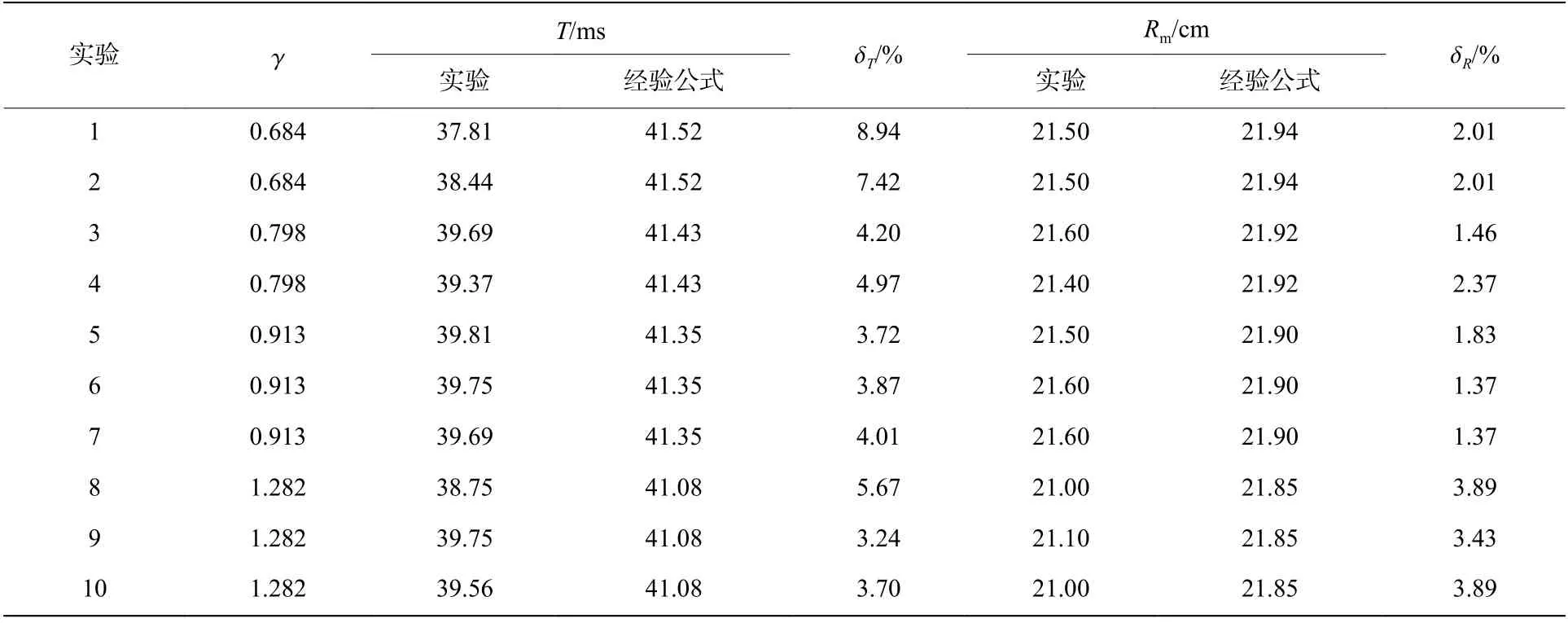
表2 气泡脉动周期和气泡最大半径的实验结果和经验公式结果Table 2 Experimental results and empirical formula results of bubble pulsation periods and bubble maximum radii

1.2.3 吸附式射流和非吸附式射流现象

高速摄影图像结果表明，炸药在固支方板底部起爆时气泡射流的演化过程可以分为两种。（1）当爆距较小（γ=0.684, 0.798）时，炸药起爆后高温高压气体产物先发生膨胀，因钢板限制了气泡的发展，气泡在膨胀至最大体积时呈上扁下圆的不规则球形。接着气泡开始收缩，由于爆距较小，气泡在收缩过程中逐渐吸附在钢板上，且已吸附的部分呈漏斗形，而未吸附的部分保持球形，吸附过程结束后，气泡整体呈漏斗形。接着气泡开始坍塌，由于漏斗形气泡底部曲率半径最小，容易发生失稳，气泡从底部开始塌陷，形成指向钢板的射流。在这种情况下，射流作用在钢板上几乎没有穿过水层，能量损耗小，此时钢板对射流的作用效果较强。（2）爆距较大（γ=0.913, 1.282）时，炸药爆炸后气泡开始膨胀，膨胀至最大体积时，气泡呈上扁下圆的不规则球形。接着气泡开始收缩，由于爆距较大，钢板对气泡的Bjerknes 引力较弱，气泡并未吸附在钢板上，而与钢板相隔一定距离继续收缩。在气泡收缩过程中，气泡底部发生坍塌，形成至下而上的射流。在这种情况下，射流在作用到钢板前需要穿过水层，因水中阻力较大，且气泡收缩过程中气泡顶部的水也以一定速度流向气泡，底部射流与顶部水流发生对流，进一步阻碍了底部射流的运动，此时射流对钢板的作用效果较弱。

2 数值模拟

为了进一步探究固支方板底部水下爆炸气泡射流的演化过程，采用ABAQUS 软件开展数值模拟。欧拉法允许材料在网格中流动，一般适用于气体及液体材料的数值模拟，拉格朗日法则常常用来描述结构的变形，而CEL 方法结合了拉格朗日法和欧拉法的优点。因此，本文中采用CEL 方法开展固支方板底部水下爆炸的数值模拟。

2.1 流体的控制方程

流体的运动都遵循流体力学的基本控制方程：连续性方程、动量方程和能量方程。认为水和空气可压缩，可压缩流体的连续性方程为：

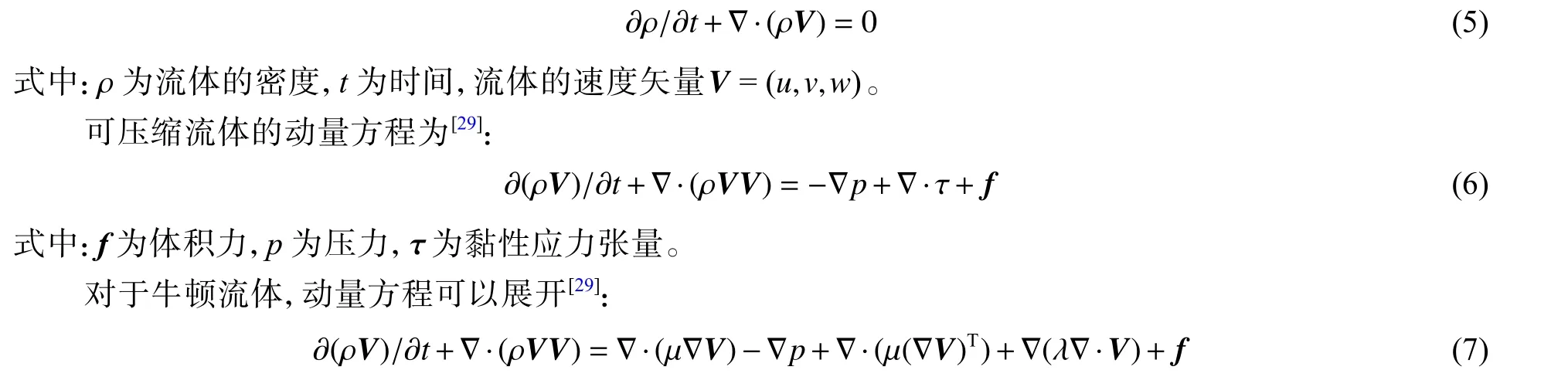
式中：为动黏性系数，λ 为膨胀黏性系数，通常λ＝-(2/3)。

2.2 流体的状态方程

在三维情况下，可压缩流体的控制方程包含6 个变量（如ρ、、、、和），但控制方程只有5 个，所以需加入描述压力和密度ρ 关系的状态方程。而一种材料存在多种不同形式的状态方程，因此选取材料的合适状态方程对数值模拟至关重要，下面给出数值模拟中的状态方程。

2.2.1 水的状态方程

水的状态方程选用Mie-Grüneisen 状态方程，该方程中压力是质量和比内能的函数，最常见形式为：

式中：为介质中的声速，为材料常数，为-方程中的常数。

本文中，水的密度为1 000 kg/m，水中的声速为1 450 m/s。

2.2.2 空气的状态方程

理想气体的状态方程为：

式中：为环境压力，为温度，为气体常数。

本文中，空气的环境压力为101 300 Pa，空气密度ρ 为1.225 kg/m，此外，还定义空气的比热为717.4 J/(kg·K)。

2.2.3 爆轰产物的状态方程

爆轰产物的JWL 状态方程为：

2.3 Johnson-Cook 材料模型

固支方板材料为Q235 钢，其材料密度为7 800 kg/m，杨氏模量为200 GPa，泊松比为0.3。Q235 钢的塑性力学性能采用Johnson-Cook 材料模型，因固支方板在实验中未发生破坏，为简化计算不引入Johnson-Cook 失效模型，因此Johnson-Cook 材料模型为：

Q235 钢的材料参数分别为：=244.8 MPa，=899.7 MPa，=0.940，=0.757，=0.039 1。

2.4 数值模拟模型

图8 为数值模拟模型示意图，采用1/4 模型，水、空气、炸药采用欧拉单元建模，采取欧拉体积分数法定义欧拉域中水、空气、炸药的尺寸及相对位置。炸药设置为直径12.5 mm、高12.5 mm 的圆柱。欧拉域顶部设置为无反射边界（Eulerian boundary＞Outflow＞Nonreflecting），欧拉域侧面和底面设置为固定边界（Symmetry/Antisymmetry/Encastre＞Encastre），对称面设置为对称边界条件（Symmetry/Antisymmetry/Encastre＞XSYMM /YSYMM）。欧拉域的网格采用非等距网格，爆心处网格尺寸为0.25 cm，最外侧网格尺寸为4 cm，欧拉域网格总数为141 万。固支方板采用壳单元建模，在固支方板角点处设置全约束边界条件，网格尺寸为4 cm。表3 为数值模拟的距离参数。

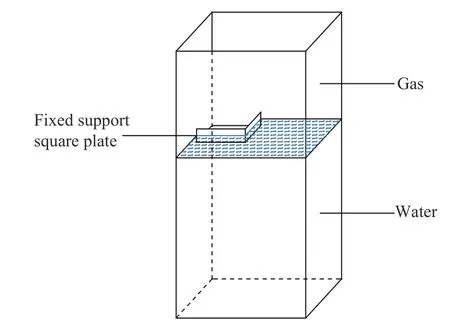
图8 数值模拟模型Fig. 8 Schematic diagram of numerical simulation model

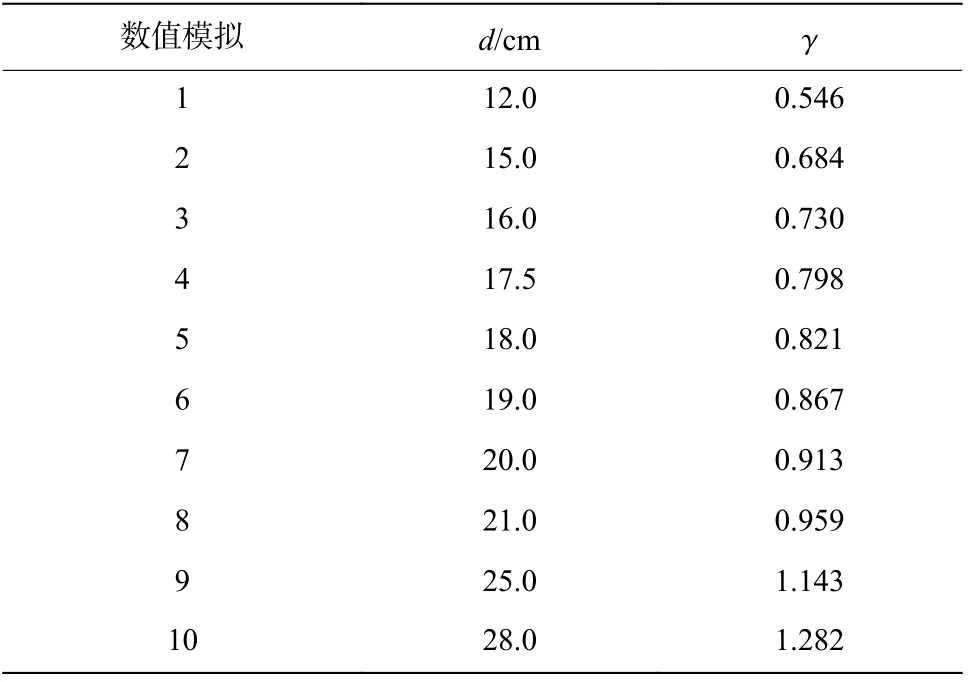
表3 数值模拟的距离参数Table 3 Distance parameters in numerical simulation

2.5 数值模拟结果分析与讨论

2.5.1 数值模拟与实验的对比

图9 为γ=0.684 时气泡演变过程的数值模拟结果与实验结果的对比。在数值模拟28.30～33.00 ms时和实验结果31.88～35.63 ms 时，气泡吸附在钢板上的过程中，其上半部分呈漏斗形，下半部分保持球形；吸附过程结束（数值模拟34.00 ms）时，气泡整体呈漏斗形；随后 （数值模拟36.00～37.20 ms），气泡底部坍塌形成射流，最后（数值模拟41.90 ms）气泡在钢板附近溃散。

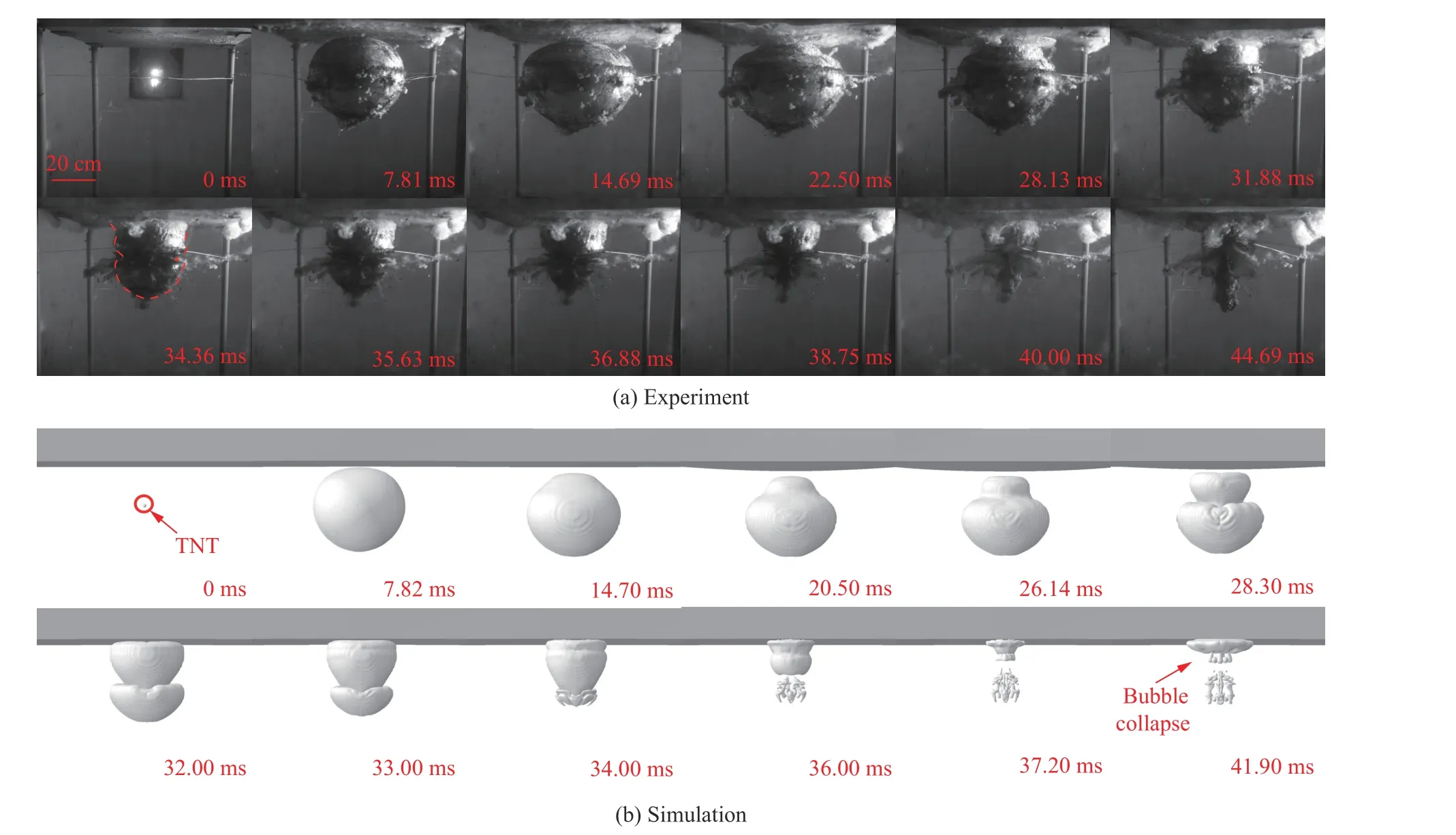
图9 当γ=0.684 时气泡演变过程的实验和数值模拟图像Fig. 9 Experimental and numerical simulation images of bubble evolution process when γ=0.684

图10 为γ=0.798 时气泡演变过程的数值模拟结果与实验结果的对比。实验和数值模拟结果均显示，气泡在收缩过程中吸附在钢板上，同时气泡吸附的过程与γ=0.684 时相似。

图10 当γ=0.798 时气泡演变过程的实验和数值模拟图像Fig. 10 Experimental and numerical simulation images of bubble evolution process when γ=0.798

图11 为γ=0.913 时气泡演变过程的数值模拟结果与实验结果的对比。数值模拟和实验结果基本一致，气泡在收缩过程中有吸附在钢板上的趋势。在数值模拟36.00 ms 时，钢板对气泡的Bjerknes 力无法使气泡完全吸附在钢板上。在数值模拟36.80 ms 时，射流发生，气泡的上表面并未贴合在钢板上。

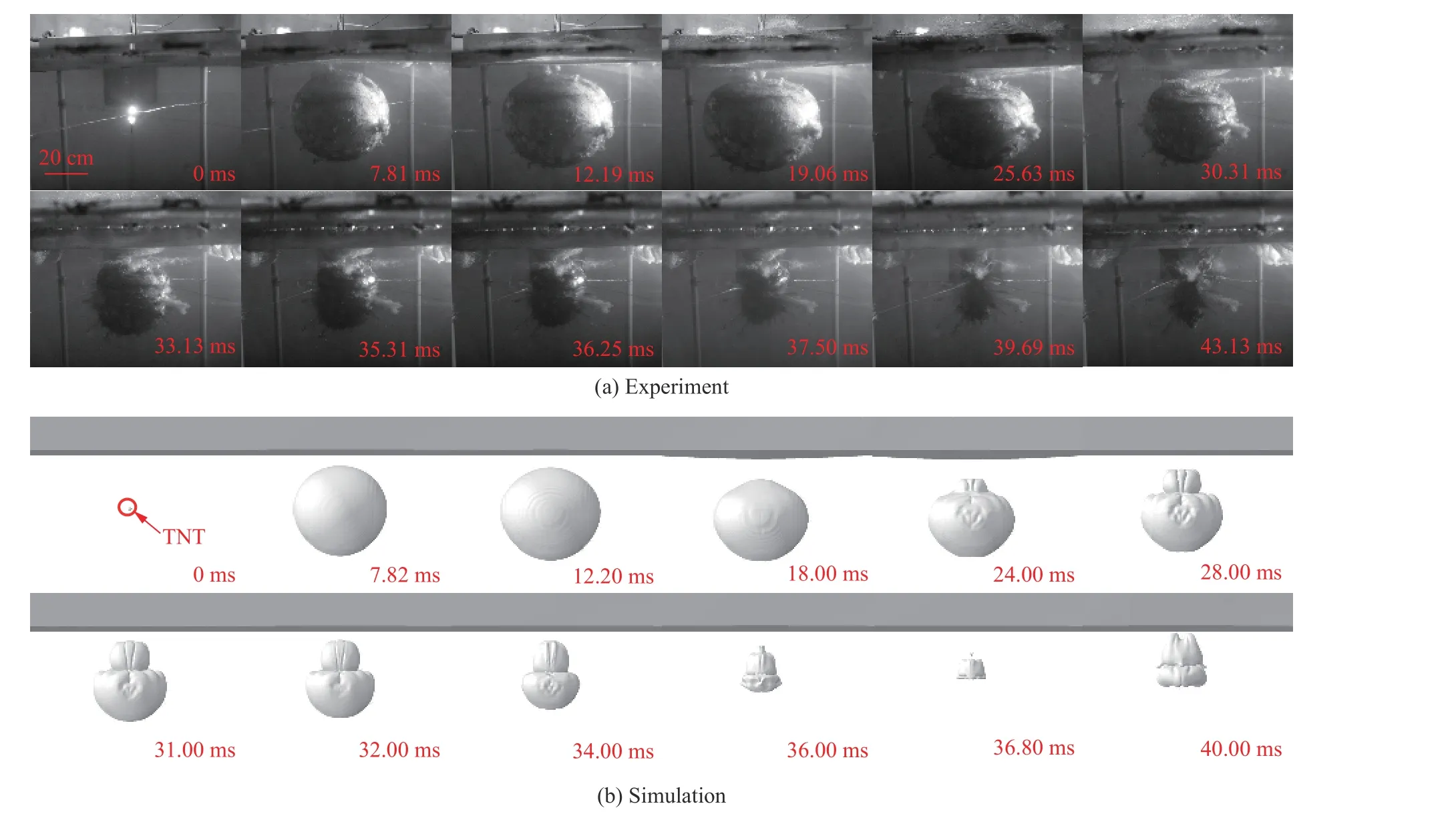
图11 当γ=0.913 时气泡演变过程的实验和数值模拟图像Fig. 11 Experimental and numerical simulation images of bubble evolution process when γ=0.913

图12 为γ=1.282 时气泡演变过程的数值模拟结果与实验结果的对比。气泡在膨胀阶段(0～19.06 ms)由球形向上边下圆的不规则球形演化。在气泡收缩阶段，气泡上表面在钢板Bjerknes 力作用下基本不发生移动，而下表面向上表面靠近，最终形成射流。在数值模拟37.00 ms 时，射流贯穿气泡，气泡演化为环状气泡。

图12 当γ=1.282 时气泡演变过程的实验和数值模拟图像Fig. 12 Experimental and numerical simulation images of bubble evolution process when γ=1.282

按照图13 的气泡上、下表面位置选取方式，图14 为γ 分别为0.684、0.798、0.913 和1.282 时气泡上、下表面位置曲线。气泡上、下表面位移曲线位移幅值的数值模拟和实验结果基本一致，但数值模拟的气泡脉动时间较短，误差在10%以内。在10～30 ms，气泡上表面位移曲线呈马鞍状，这是因为：钢板受冲击波作用后开始振动，顶部固支方板先向下运动，使气泡上表面下移，随着钢板的回弹，气泡上表面发生上移。

图13 气泡上、下表面Fig. 13 The upper and lower surfaces of a bubble

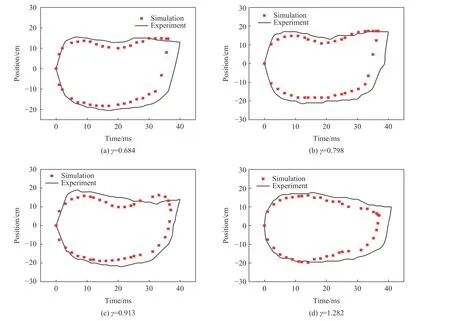
图14 气泡上、下表面位置曲线Fig. 14 The positions of the upper and lower surfaces of a bubble

2.5.2 吸附式射流向非吸附式射流转化的临界点

图15～16 分别为γ=0.821, 0.867 时气泡演化过程的数值模拟图像。当γ=0.821 时，在气泡收缩阶段（19～37 ms），气泡在钢板Bjerknes 引力作用下整体吸附在钢板上，产生吸附式射流。当γ=0.867 时，在气泡收缩阶段（19～37 ms），气泡受到钢板Bjerknes 引力的作用，部分气泡向钢板运动，呈现吸附的趋势，但钢板对气泡的Bjerknes 引力不足以使气泡完全吸附在钢板上，在气泡坍塌阶段并未发生吸附式射流，见37 ms 时图像。因此，吸附式射流向非吸附式射流转化的临界点在γ=0.821～0.867。炸药起爆时，因钢板的阻挡，气泡上半部分难以自由膨胀，使气泡发生吸附时对应的爆距小于1 倍最大气泡半径，依据本文的数值模拟结果，临界点在γ=0.821～0.867。

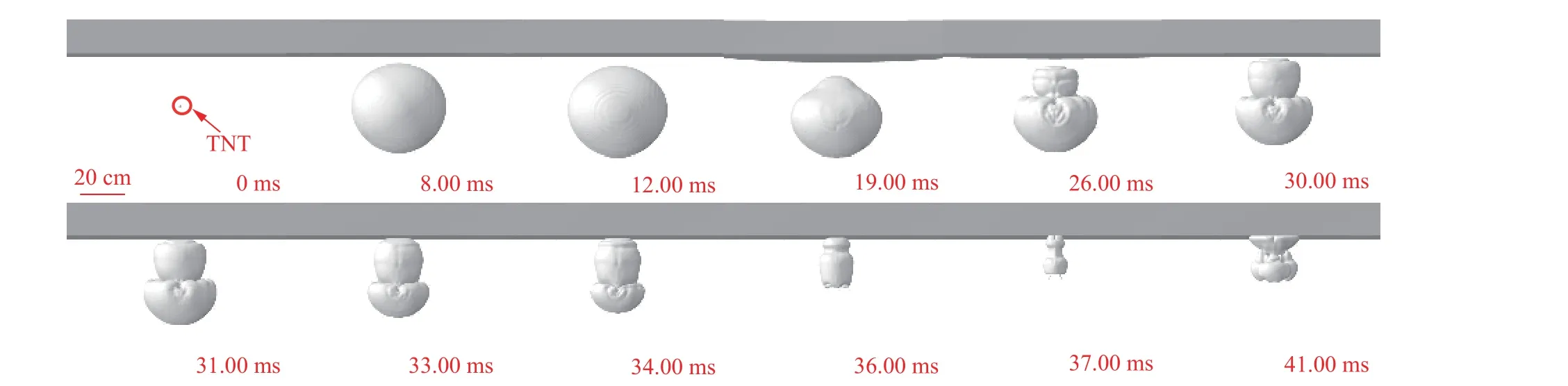
图15 当γ=0.821 时气泡演变过程的数值模拟图像Fig. 15 Numerical simulation images of bubble evolution process when γ=0.821

图16 当γ=0.867 时气泡演变过程的数值模拟图像Fig. 16 Numerical simulation images of bubble evolution process when γ=0.867

2.5.3 爆距对射流速度特性的影响

图17 为水射流顶部节点（气泡底部节点）的速度曲线，图18 为不同爆距下射流速度云图演化的数值模拟图像。当γ=0.546～0.821 时，射流均从气泡底部开始形成，随着爆距的增加，气泡在射流形成阶段的形状越来越细长，气泡底部的曲率越来越大，导致射流速度随着爆距增大而增加。当γ=0.867 时，随着爆距的增加，钢板对气泡的作用效果减弱，在射流阶段气泡明显脱离钢板，同时射流速度减小。当γ=0.913 时，能看到36.60 ms 时气泡顶部形成一束射向下方的射流，但因钢板Bjerkness 引力的限制，顶部向下的射流难以继续演化，同时，气泡底部在钢板Bjerkness 引力和浮力的作用下形成由气泡底部射向气泡顶部的射流，在37.00 ms 时能看到两股射流相互作用，形成了对射流。当γ=0.959 时，看到36.60 ms 时从气泡顶部形成一束裙摆状射流向下运动，同时，气泡底部发生失稳形成一束更强的射流向上运动，两股射流形成了对射流。当γ=1.143, 1.282 时，现象较相近，在射流形成阶段，气泡上表面位置保持不变，气泡下表面向钢板运动，在浮力和Bjerkness 引力作用下底部进一步坍塌，最终形成射流，但由于爆距较大，Bjerkness 引力较弱，形成的射流速度也较低。综上所述，随着爆距的增大，射流速度先增大后减小，在吸附式射流和非吸附式射流转化的临界点附近，射流速度达到最大。

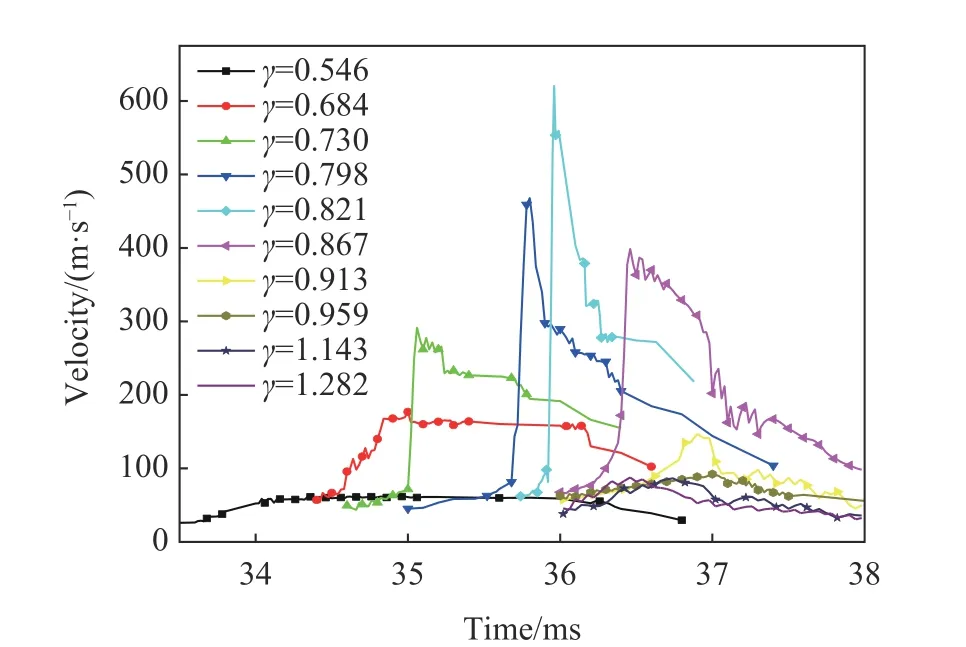
图17 在不同距离参数下射流顶部节点的速度曲线Fig. 17 Velocity curves of jet top nodes under different burst distances

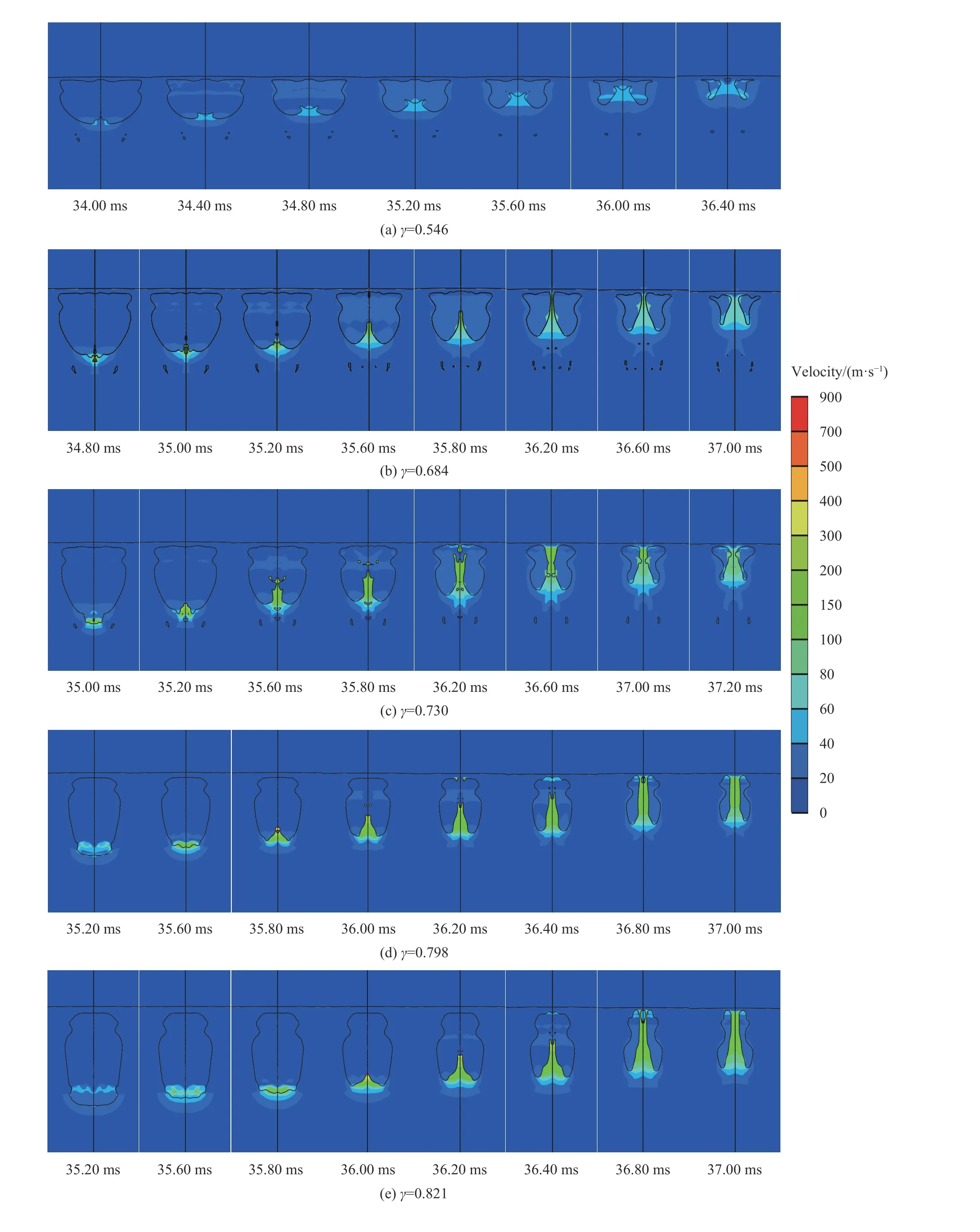
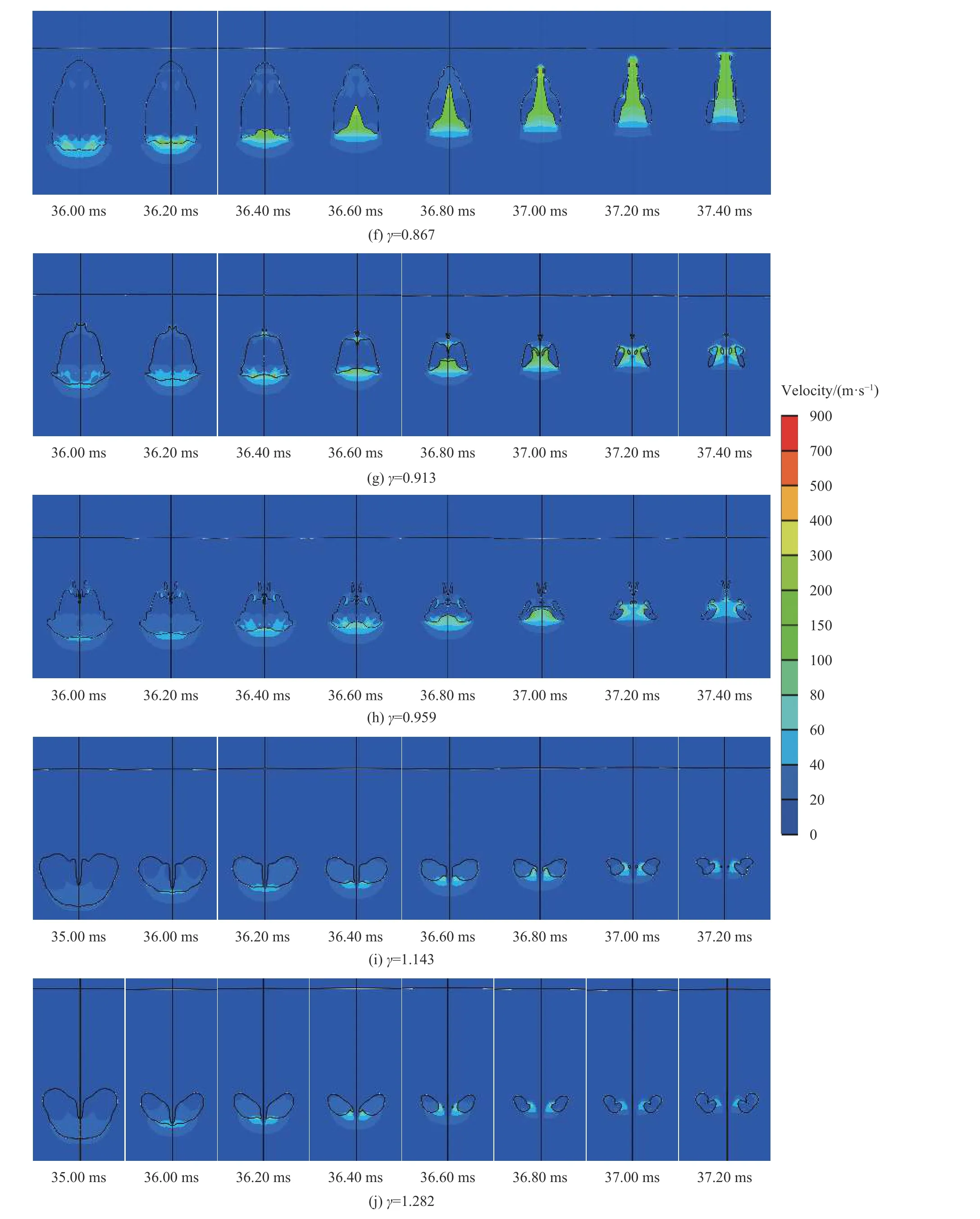
图18 在不同距离参数下射流速度演化过程的数值模拟图像Fig. 18 Numerical simulation images of jet velocity evolution processes at different burst distances

图19 为不同距离参数下射流开始形成的时间，以图17 中速度曲线起始阶段的拐点作为射流形成时间。当γ0.867 时，射流形成时间随着爆距增加而增加，当γ≥0.867 时，射流形成时间随着爆距增加基本不变。这说明，顶部固支方板加速了气泡坍塌形成射流的过程，与张阿漫等的观点一致。本文中还发现：发生吸附式射流时，爆心离固支方板越近，射流形成时间越早；发生非吸附式射流时，射流形成时间不受爆距影响。拟合可得射流形成时间（ms）与距离参数γ 的关系（相关系数为0.993 7）：

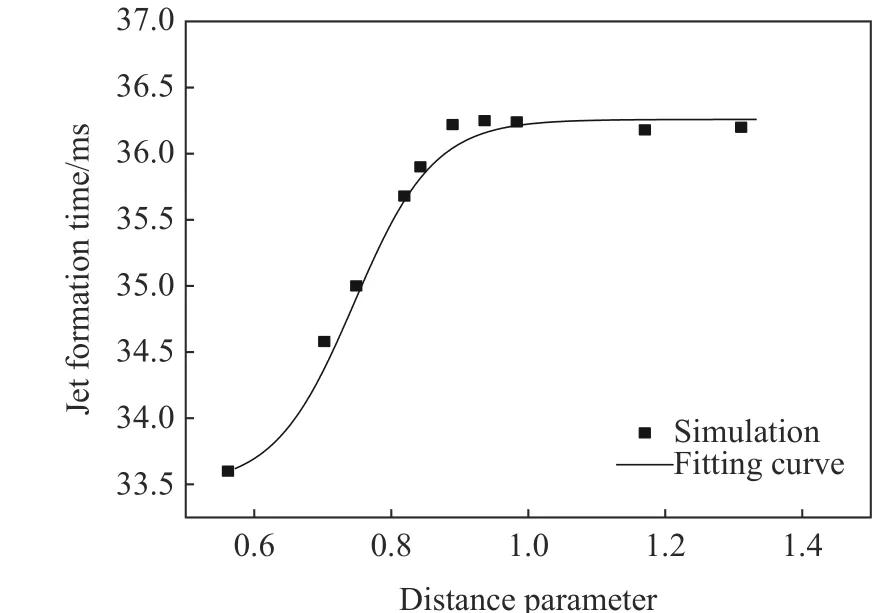
图19 射流形成时间与距离参数的关系Fig. 19 Relationship between jet formation time and distance parameter

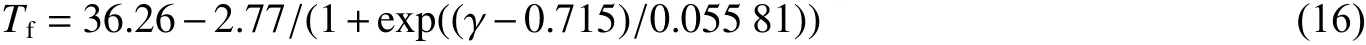
图20 为不同距离参数下射流的最大速度及达到最大速度时对应的时间。发生吸附式射流时，射流最大速度随着爆距的增加而增加，且射流达到最大速度出现的时间越来越迟，这是因射流形成时间变迟导致的；发生非吸附式射流时，射流最大速度随着爆距的增加逐渐减小，当γ≥0.959 时，射流最大速度基本保持不变，而射流最大速度出现的时间越来越早。可拟合得到射流最大速度（m/s）与距离参数γ 的关系（相关系数为0.896 0）：

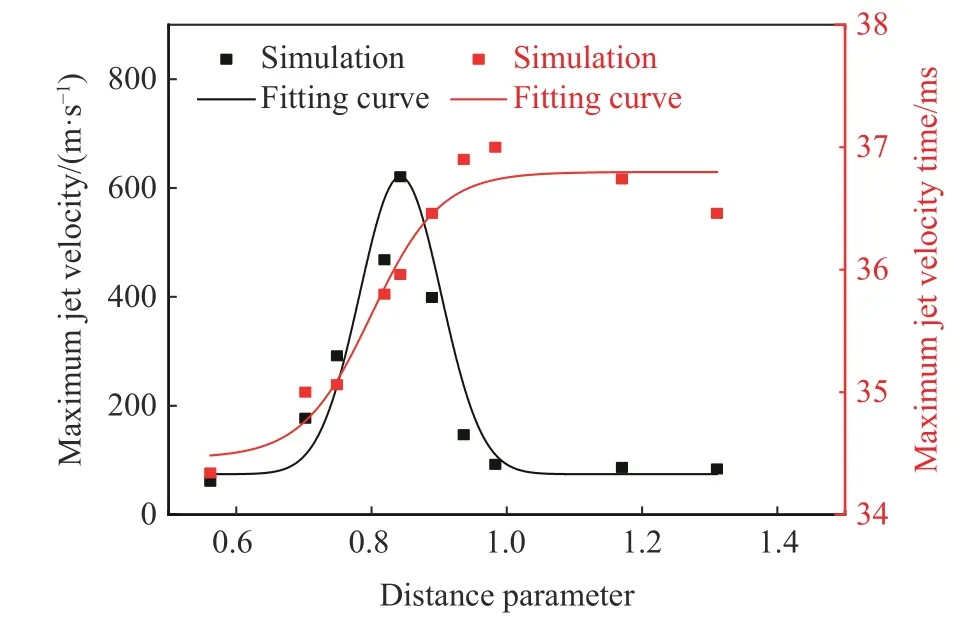
图20 不同距离参数下最大射流速度和最大射流速度时间Fig. 20 Maximum jet velocities and maximum jet velocity times at different distance parameters

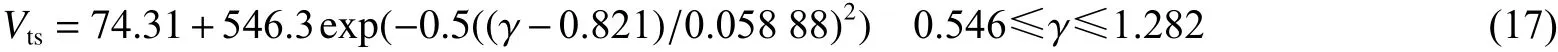
和射流达到最大速度的时间（ms）与距离参数γ 的关系（相关系数为0.948 5）：

图21 为不同爆距下射流击中钢板时的速度，当γ≥0.959 时射流未能到达钢板，因此图中没有显示。当γ≤0.821 时，射流击中钢板时的速度和射流击中钢板时的时间都随着爆距的增大而增大；当0.821＜γ≤0.913 时，射流击中钢板时的速度随着爆距的增加迅速减小。这是因为，发生非吸附式射流时，钢板与气泡间存在较厚的水层，射流在穿过水层时速度迅速衰减，导致射流速度降低。当γ＞0.959 时，因射流在水层中的衰减效应和对射流现象，导致射流未能到达钢板。拟合可得射流击中钢板时的速度（m/s）与距离参数γ 的关系（相关系数为0.995 5）：

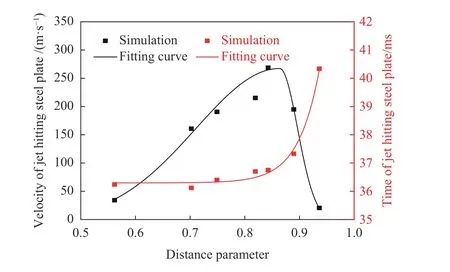
图21 不同距离参数下射流击中钢板的速度和时间Fig. 21 Velocities and times of jet hitting steel plate at different distance parameters

3 结 论

开展了TNT 炸药在水面固支方板底部不同爆距下的水下爆炸实验，观测了距离参数γ=0.684～1.282的气泡射流现象，通过水下压力传感器测得了冲击波和气泡脉动的压力数据，基于ABAQUS 软件，采用CEL 方法开展了系列数值模拟。在此基础上，得到如下结论。

（1）高速摄像图像显示：当距离参数γ=0.684, 0.798 时，气泡吸附在钢板上，形成吸附式射流；当γ=0.913, 1.282 时，气泡未吸附在钢板上，形成非吸附式射流。

（2）数值模拟结果表明，吸附式射流向非吸附式射流转化的临界点在距离参数为0.821～0.867。这是由于，在钢板的阻挡下，气泡上半部分难以自由膨胀，使气泡发生吸附时对应的爆距小于1 倍最大气泡半径。

（3）在吸附式射流对应的爆距范围内，爆距越小，射流形成时间越早，说明顶部固支方板加速了气泡坍塌形成射流的过程，且气泡距离钢板越近，这种加速效果越明显。但在非吸附式射流对应的爆距范围，固支方板对气泡坍塌过程的影响较弱。

（4）在吸附式射流对应的爆距范围，随着爆距的增加，射流形成过程中的最大速度越大，射流达到最大速度的时间越迟，射流速度最大值可达到621 m/s。这是因为，爆距越大气泡坍塌时间越迟，气泡能量越集中，因此形成的射流速度越大。而在非吸附式射流对应的爆距范围，随着爆距的增大，射流最大速度迅速下降，当γ≥0.959 时，射流最大速度基本为约100 m/s，最大速度出现的时间在小范围内变动。

（5）射流击中钢板时的速度随着爆距的增大先升后降，在临界点附近最大值可达到269 m/s，射流击中钢板的时间随着爆距的增加持续增加。由于水流的阻挡，当γ≥0.959 时，射流未击中钢板。