基于退相关DIC 的疲劳裂纹全局动态测量方法1)

程斌 李得睿

(上海交通大学船舶海洋与建筑工程学院,上海 200240)

引言

疲劳裂纹广泛存在于各类工程材料及结构中,对安全性和耐久性产生了严重影响.近几十年来,国内外大量工程(如钢结构工程)都出现了不同程度的疲劳开裂破坏事故.对于此类问题,首先需要对已有裂纹的尺寸分布情况进行检测,在此基础上对结构的剩余使用寿命开展评估,以确定后续养护维修策略.对于暂时无需维修加固的裂纹,则应加强对其后续扩展过程的跟踪检测或测量,以定期更新结构状态评估的结果,并及时采取措施.另一方面,在几乎所有的疲劳试验中,对疲劳裂纹萌生及扩展全过程的尺寸测量是必不可少的一环.因此,开展疲劳裂纹全局动态测量研究具有重要意义[1-5].

但由于疲劳裂纹的开裂模式具有多样性,细观疲劳裂纹多出现在焊缝、开孔等局部区域,且裂纹在反复荷载作用下具有开合“呼吸”特征,这对裂纹测量提出了高要求.现有的人工目测、超声、射线、磁粉、液体渗透等疲劳裂纹检测测量方法均存在过程繁琐、稳定性差、精度低等不足,这已成为疲劳裂纹测量领域的“卡脖子”问题之一.

目前已有众多学者采用传统图像处理及机器学习方法,识别并测量结构物裂缝或裂纹,但此类方法难以应用于需要高精度和动态追踪的疲劳裂纹测量.王睿和漆泰岳[6]提出了基于数字图像及RBFSVM 分类模型的裂缝识别方法,实现了较为高效的裂缝识别;路永祥[7]采用灰度直方图、均值滤波等传统图像处理技术,静态量测了发动机金属元器件表面的疲劳裂纹形态;刘宇飞等[8]总结并展望了各类基于数字图像的结构表面裂缝识别方法,并报道了基于无人机平台的裂缝识别研究与应用;Nguyen等[9]提出了二阶段卷积神经网络算法,用于识别并分割道路图像中的裂缝病害,测试精度达到整像素级别;晏班夫等[10]提出了基于Faster R-CNN 与图像形态法的路面病害识别方法,实现了准确、高效的路面裂缝识别;杨娜等[11]提出了基于无人机与改进SIFT-RANSAC 算法的木结构裂缝测量系统,并基于实例模型验证了该裂缝测量系统的可行性.以上基于传统图像处理及机器学习方法的裂纹识别技术,仅可实现静态裂纹测量,测量精度为整像素级别.

数字图像相关(digital image correlation,DIC)技术已广泛应用于各类力学测量领域,但由于裂纹开裂导致的DIC 退相关效应(计算失效),一直阻碍DIC 在裂纹测量方面的应用.对此,各国学者开展了相关研究,试图规避或解决此类退相关问题.汤文治等[12]基于子区分离模型提出了非连续DIC 方法,实现了裂纹区域位移场的静态重构;Sutton等[13]基于DIC 测量了有机玻璃附近的表面位移场,并验证了J 积分的路径无关性;Hassan等[14]同时考虑了子区的分割及距离,实现了裂纹量测位移场测量;Jay等[15]将DIC 技术用于处理微观高分辨率视场下的疲劳裂纹图像,基于非连续应变场测试结果,揭示了疲劳裂纹在亚晶格下的萌生过程;Qvale等[16]采用DIC 形变场测试技术及参数优化方法,对疲劳裂纹的应力强度因子及生长周期进行了准确测试,测试结果与传统方法吻合良好;杜鉴昕等[17]提出了一种基于Hermite 单元的局部DIC 方法,可用于准确计算裂纹尖端的形变场;Sánchez等[18]采用DIC 技术对遭受腐蚀侵害的海上系泊链进行了点云形变场测试,通过非连续形变场测试结果判断系泊链表面裂纹的萌生及发展时刻;朱志辉等[19]运用DIC 与无网格技术的混合方法,准确测得了裂纹尖端的应变分布.谷柳凝等[20]提出了基于DIC 主应变场的混凝土全表面开裂特征实时测量方法,该方法具备0.01～0.017 像素的裂纹宽度测量精度.但这些研究主要针对裂尖局部区域或裂纹形变场进行测试,无法实现疲劳裂纹全局形态及尺寸的动态测量及可视化,且存在计算复杂、实现困难等方面的不足.

由于图像纹理退相关导致DIC 目标点计算失效的问题,一直是DIC 的核心痛点问题,这个问题通常是需要被极力规避的.然而,本文恰巧利用了此DIC 技术缺陷.裂纹开裂反映到图像,本质上就是图像纹理破坏,也称作图像纹理退相关效应,所以图像内裂纹开裂会导致DIC 目标点计算失效,也即目标点计算失效信息中蕴含了裂纹信息.本文试图从计算失效信息中提取裂纹信息,为此提出了一种疲劳裂纹全局动态测量算法.本文通过DIC 算法开发,提出一种基于数字图像相关及退相关原理的疲劳裂纹动态测量方法,并通过数值模拟与钢节点疲劳试验,验证本文方法的准确性和有效性.

1 疲劳裂纹DIC 算法

1.1 DIC 基本原理

DIC 的基本原理是对一固定像素区域的图像数据在时间域内进行亚像素级别的高精度位移追踪.例如对于某一尺寸的像素子区,像素子区的中心即为目标点,DIC 算法核心在于精确追踪这个目标点所在像素子区的形状变化过程,从而得到该目标点的位移时程数据.实际处理过程中,可采用不同阶数的形函数对小区域像素子区进行形状拟合,形函数阶数越高,其对变形的拟合能力越强,图1 为常用的零阶和一阶形函数示意图.目前,DIC 主流亚像素算法包括前向累加牛顿拉弗森算法(forward-additive Newton-Raphson,FA-NR)[21]和反向组合高斯牛顿(inverse-compositional Guass-Newton,IC-GN)[22-23]算法,此类算法通过亚像素迭代方式,基于形函数精确拟合逼近得到像素子区的量化形变过程.无论整像素算法还是亚像素算法,本质上都是对相关度函数进行寻优,DIC 主流的相关度函数包括零均值归一化最小平方距离(zero-mean normalized sum of squared difference,ZNSSD)函数与零均值归一化互相关(zero-mean normalized cross correlation,ZNCC)函数,这两者是等价的,可线性互转化[22].图像纹理退相关则会导致较低的ZNCC 计算结果,也即DIC计算失效.

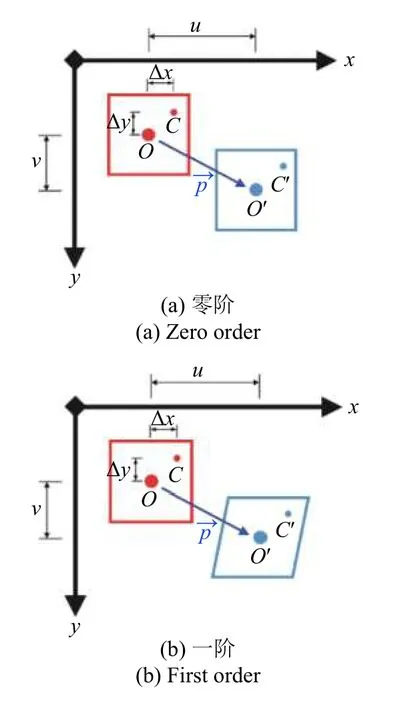
图1 形函数示意图Fig.1 Shape functions

将DIC 算法用于追踪图像内的目标点云,在时间域内可得到各目标点的位移时程数据,在空间域内即可得到位移场.位移场测试中,通常需包含5000 以上的DIC 目标点数量,在高分辨率高精度情况下,甚至可包含数十万数量级的目标点.应变场测量方面,目前DIC 领域主流的应变场算法多为后处理算法[24-26],算法原理多为位移场差分及数据平滑.

1.2 DIC 点云拓扑结构

基于目标点云计算得到位移场后,为了从中提取疲劳裂纹形态,需要事先在点云内部建立一种有机的拓扑结构,该结构可表示点云内部各个目标点之间的连接关系,且该连接关系不随点云几何形状改变而变化.

如图2 所示,圆点表示单个DIC 目标点,点内数字为该目标点编号,所有圆点组成了DIC 目标点云.建立拓扑结构时,遵循由左到右、由上到下的原则,逐点递增为各目标点建立编号.进一步建立目标点云拓扑表,以便可以迅速查找到某目标点上下左右4 个目标点的编号,实际可从该目标点上方的目标点开始,按顺时针方向,依次存储该四个邻近目标点编号.如果该目标点在对应方向上没有邻近目标点,则将相应的编号赋值为-1.由此建立的点云拓扑表,采用二维数组或结构体数组进行存储.该点云拓扑表不受目标点云几何形状的影响,也即在任何情形下,均可快速查找得到某目标点的各相邻目标点编号,进而在位移场数据中查找得到相邻目标点的位移结果.

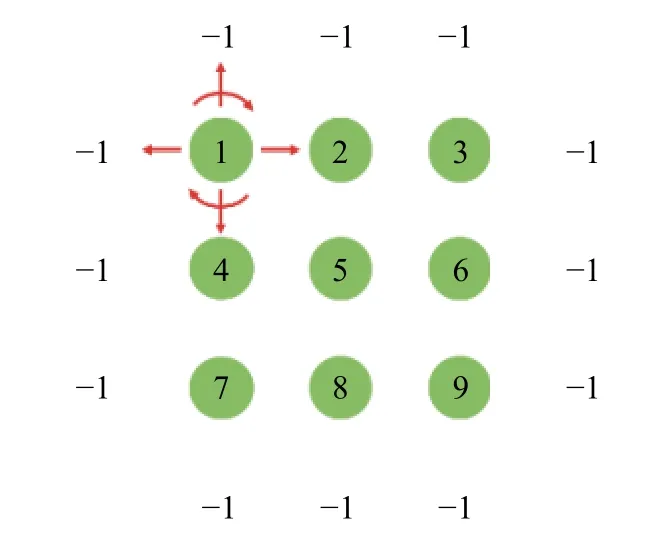
图2 DIC 点云拓扑结构Fig.2 Topological structure of DIC point cloud

1.3 裂纹灭点剔除

疲劳裂纹萌生及扩展过程中,对应图像纹理发生破坏,也即图像纹理退相关,从而导致位于裂纹区域的DIC 目标点计算失效.本文将这些计算失效的目标点称为灭点,反之为生点.通过灭点可得到裂纹信息.因此对于每一帧图像,需要对裂纹及其附近区域目标点的生灭情况进行判定,以灭点代表实际开裂范围并对其进行剔除,进而计算得到裂纹边界及相关尺寸数据.

本文采用IC-GN 算法对ZNSSD 相关度准则进行最优化迭代计算,并将优化后的ZNSSD 值线性换算为对应的ZNCC 数值[22].ZNCC 函数[27-28]具备出色的抗干扰能力,且值域范围固定,可有效评估两数据集间的相关度.假设有引用图像f(x,y)与匹配图像g(x′,y′),图像尺寸均为M×M像素,当g(x′,y′)线性变化为g′(x′,y′)后,二者进行ZNCC 互相关运算,依旧有R′ZNCC,f,g′≡RZNCC,f,g,可见ZNCC 相关度函数具备强抗干扰性,无论g(x′,y′)发生比例 变化还是平移变化,RZNCC结果始终保持不变.同时,ZNCC 系数的值域范围为RZNCC∈[-1,1],符合直观的置信度数值范围,非常适用于评判DIC 两图像子区的相关置信度.

实际计算时,取ZNCC 置信度阈值为0.8～0.9[29-30],低于此阈值的目标点被判定为灭点,不再参与后续计算.实测中可采用0.85 作为较保守的ZNCC 置信度阈值.需要说明的是,光照变化、形函数不匹配等可能导致相关系数计算结果降低.于本方法而言,采用ZNCC 相关函数进行相关度运算可基本消除光照变化的影响,而形函数不匹配多由于散斑特征不达标或DIC 子区尺寸选取不恰当所致,因此在测量准备及后处理过程中应多加注意,以提升本文方法的鲁棒性.

1.4 裂纹边界重构

1.4.1 离散生灭边界提取

在判定了DIC 目标点云中所有的生点和灭点之后,需要进一步确定生点与灭点之间的界限(简称生灭边界),因为其蕴含了裂纹上下两个边界的形态信息.本文结合DIC 点云拓扑结构,提出一种“三生点”算法,该算法的作用在于从位移场目标点中提取得到生灭边界.该算法认为某目标点的四个邻近目标点中,若存在三个生点和一个灭点,即判定该目标点处于生灭边界.

运行“三生点”算法时,需遍历点云内的全部目标点,对每个目标点的拓扑表存储编号进行依次排查,若第i个目标点顺时针方向上存在连续排布的三个生点与一个灭点,则认为该目标点是生灭边界的组成部分,并进行存储.图3 为生点类型示意图.图4 为一组连续的直线裂纹模拟图像,开裂角度从0°以0.2°为级差分步增大至1°,由此得到6 张裂纹图像.对模拟图像序列运行本文方法,即可得到图4中的运算过程可视化结果,由于模拟直线裂纹以每帧0.2°的速率缓慢张开,所以通过结果可以看出,直至处理到第4 张图像后,本文方法对生灭边界的提取已趋于稳定.图4 中的黄色边界即为“三生点”算法得到的生灭边界结果,可以看到,第4 帧图像之后的黄色边界已趋于稳定.将这些生灭边界上的目标点进行组合,即可得到由离散目标点组成的裂纹离散边界,该边界分别对应于裂纹的两侧边界,本文将此离散边界称为裂纹双链.对于常见的单向、平滑裂纹边界,进行离散目标点组合时,可基于所有离散点拟合出一条直线,以此直线为x轴、直线法向为y轴建立局部坐标系,将所有点映射至此局部坐标系后按x坐标值大小进行排序,即可实现离散目标点组合.需要说明的是,组合算法是不唯一的,可根据裂纹的不同形状特点进行开发实现.

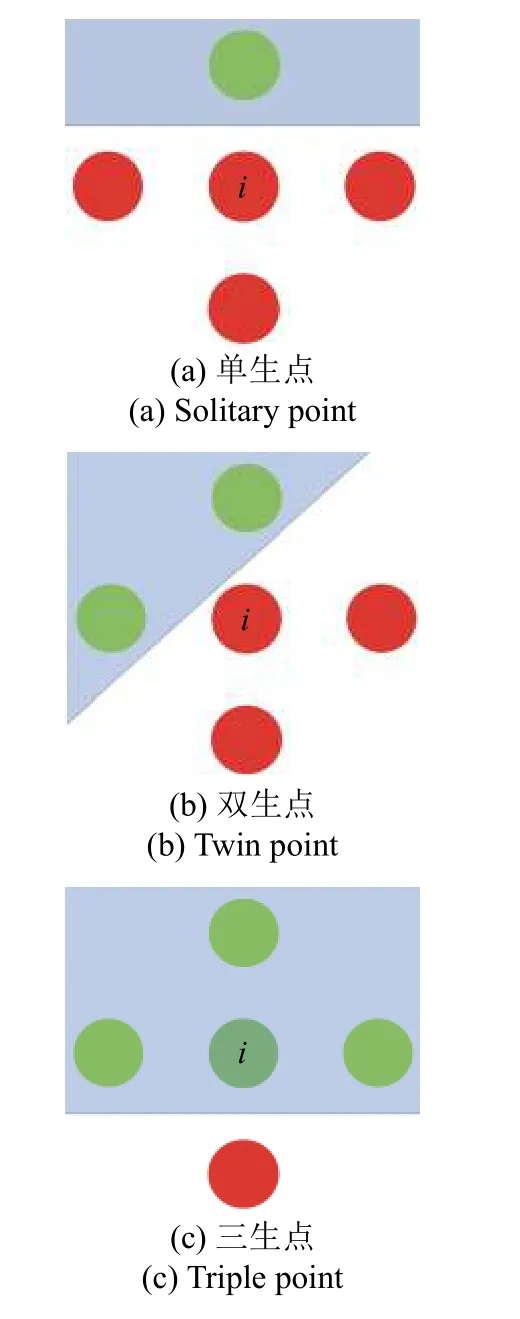
图3 生点类型示意图Fig.3 Types of inclusive data point

图4 模拟裂纹图像Fig.4 Pictures of simulated cracks

1.4.2 裂纹双链内推

以上DIC 目标点运算过程依靠像素子区内的数据进行迭代,当裂纹穿过某像素子区时,该像素子区内图像纹理被破坏,其ZNCC 计算结果均低于阈值,对应的目标点被判定为灭点.而那些像素子区边界与真实裂纹边界相邻却又未被裂纹边界穿过的目标点,则被判定为三生点(即离散双链目标点).因此,通过“三生点”算法得到的离散边界并非裂纹的真实边界,其与裂纹真实边界还存在一定距离,该距离与DIC 目标点所在的像素子区尺寸有关.因此,可对裂纹离散双链进行内推,使之与真实裂纹边界相吻合,本文将内推得到的点称为离散边界点.由于目标点处于像素子区中心,因此内推距离取为正方形像素子区的半高度.内推方向为目标点所在邻近边界的法向.

1.4.3 裂纹边界拟合

进一步对内推得到的离散边界点进行拟合,即可得到由两条连续曲线表示的裂纹形态.由于多数疲劳裂纹边界在宏观尺度下表现为单向、平滑且连续的曲线.因此本文采用四次函数曲线对离散边界点进行拟合,拟合算法采用最小二乘法.

假设某个单链内共有N个边界点,第i个边界点的坐标为(xi,yi),采用四次多项式对这些边界点进行表示如下

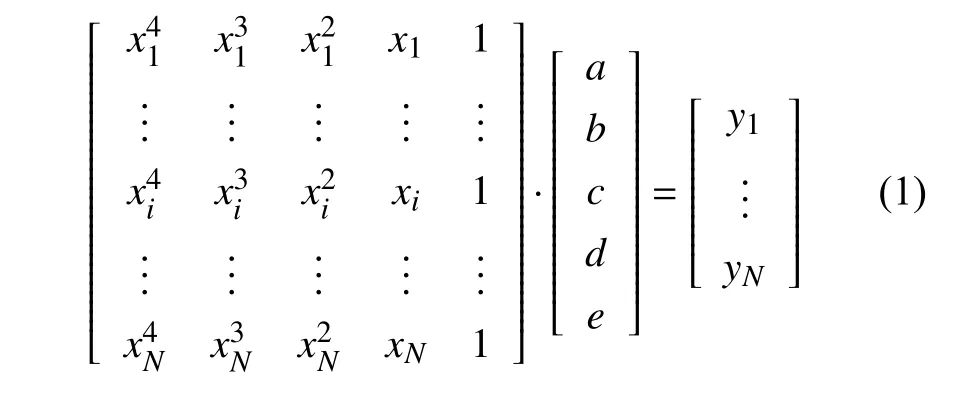
其中,a,b,c,d,e为四次多项式系数,i∈[1,2,···,N]且N≥ 5.

该方程组简化表示为

其中,X为中x坐标矩阵,Y为中y坐标矩阵,A为系数矩阵.

进而采用最小二乘法可得

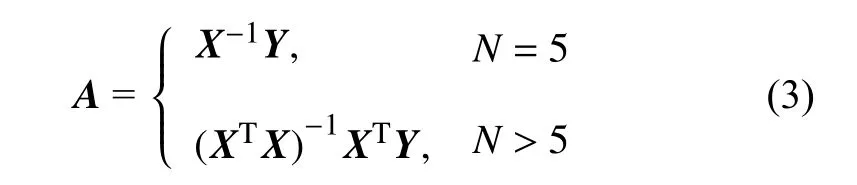
基于拟合得到的裂纹连续边界,可进一步计算得到不同部位的裂纹宽度值,并通过积分得到裂纹的总长度值,为疲劳裂纹尺寸测量提供数据.需要说明的是,本文主要针对金属结构常见的单向、平滑裂纹采用四次函数拟合,但拟合方法并不唯一,对于岩石裂纹、混凝土裂纹等复杂形状裂纹,则可以采用分段样条拟合.

1.5 方法流程

本文提出的疲劳裂纹动态测量方法具体步骤流程见图5.该方法首先针对工业相机拍摄得到的每一帧裂纹图像,采用DIC 算法追踪得到目标点云位移场,并建立DIC 点云的有机拓扑结构,再基于零均值归一化互相关准则判别裂纹灭点并建立裂纹的上下双链离散边界,最后通过数值拟合得到裂纹的连续边界,建立一套完整的裂纹形态重构算法.在此基础上将该算法应用于逐帧图像,即可得到疲劳裂纹形态、长度、宽度等指标的量化变化过程,实现疲劳裂纹动态扩展全过程的精细化智能测量.

图5 方法流程图Fig.5 Flowchart of proposed method

2 裂纹模拟试验

2.1 数值模拟裂纹

2.1.1 裂纹模拟图像

首先基于数值模拟对本文提出的方法进行验证.选取国际力学协会开源DIC 试验数据Sample13[31-32]的第一张图像作为模拟裂纹闭合状态,图像宽1040像素,图像高1392 像素,如图6(a)所示.在此基础上,以图像左上角为原点、x轴向右为正、y轴向下为正建立图像坐标系,插入以下方程曲线作为裂纹上边界

式中,yc为裂纹上边界的y坐标,W为图像宽度,H为图像高度,x∈[0,W].该余弦曲线与典型疲劳裂纹的单向、平滑、连续特征相吻合,并且线条走势较为丰富,可兼容多数情况下的疲劳裂纹边界形态.

进一步以该曲线作为分割线,将图像分为上、下半幅,对下半幅图像以图像左边界中点(x=0,y=H/2)为原点,顺时针旋转1°,从而得到裂纹张开状态图像,如图6(b)所示.裂纹上边界旋转之后得到的曲线即为裂纹下边界.

图6 曲线裂纹模拟图像Fig.6 DIC pictures of simulated cracks

2.1.2 裂纹重构结果

基于以上裂纹闭合和张开的两张DIC 图像,运用本文方法对模拟裂纹边界进行重构,并验证其精确性.

模拟裂纹的重构结果见图7,其中图7(a)为裂纹的生灭边界提取结果,图7(b)为由生灭边界内推得到的边界离散点,图7(c)为边界离散点经过最小二乘拟合后得到的连续曲线,代表裂纹边界的最终重构结果,四次多项式系数a～e的拟合结果见表1.

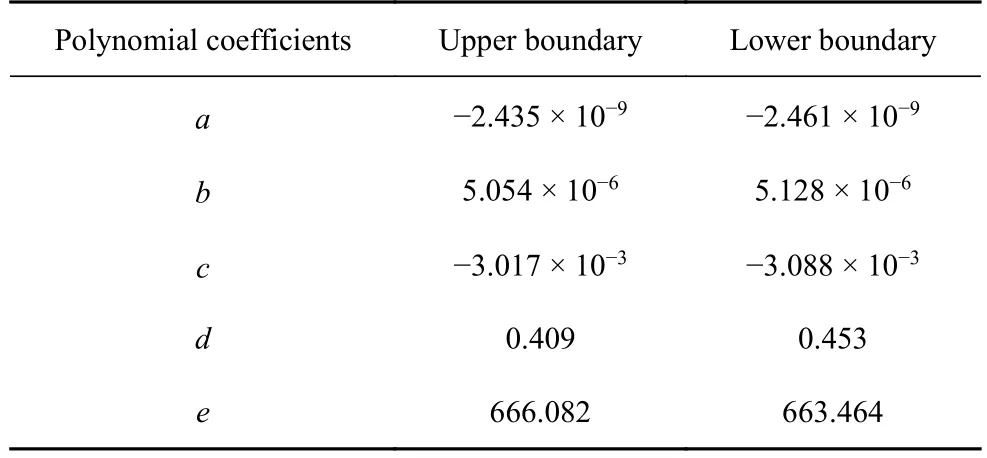
表1 裂纹边界重构结果Table 1 Parameters of simulated crack reconstruction results

图7 模拟裂纹的重构结果Fig.7 Reconstruction of simulated crack

2.1.3 裂纹重构精度验证

选取裂纹边界左右端点之间的数据进行验证.以裂纹上边界为例,记实际边界函数为yc(x),模拟边界函数为ys(x),裂纹左端点横坐标为xa、右端点横坐标为xb.将裂纹边界曲线按横坐标值均分为N段,则第i段右端点的重构误差可表示为

其中,N为正整数,i∈ [0,1,2,···,N].

将各点误差值取均方根,得到单条边界的RMS误差为

本例取N=200,得到裂纹上、下边界的RMS误差值分别为0.411 像素和0.420 像素,边界各点的误差像素值分布如图8 所示,可见裂纹边界重构的整体精度非常高.

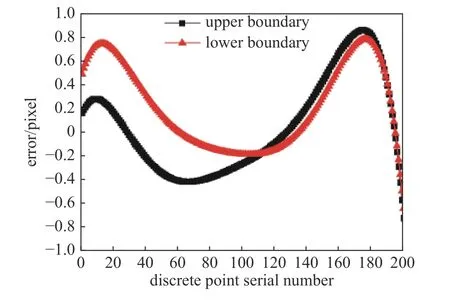
图8 裂纹边界重构误差分布Fig.8 Reconstruction errors of crack boundaries

基于裂纹边界的重构曲线,积分得到裂纹长度测量值,并选取裂纹起点、中点、终点三个位置的宽度测量值,与裂纹理论尺寸的对比结果如表2 所示.裂纹宽度测量精度非常高,误差均在0.08 个像素以内,裂纹长度测量误差沿长度方向有所累积,但也仅为0.462 个像素,说明本文测量方法具有极高的准确性.

结合实际测量场景,对本文算法的精度作进一步分析.假设相机的横向分辨率为W,裂纹在图像横向上的像素投影长度占相机横向分辨率的比例为a,裂纹在相机坐标系横轴上的投影长度为L,算法理论误差为RMS,此时可估算得到实测误差为

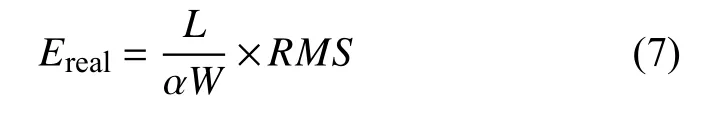
考虑典型情况,取a=0.8,W=1920,L=200 mm,基于表2 误差数据,对于裂纹长度和宽度测量,分别取RMS为0.5 和0.1 像素,可得Ereal值分别为0.065 mm 和0.013 mm.考虑这些参数的可能浮动范围,一般也能满足Ereal＜ 0.1 mm,可见本文算法具有很高的计算精度.

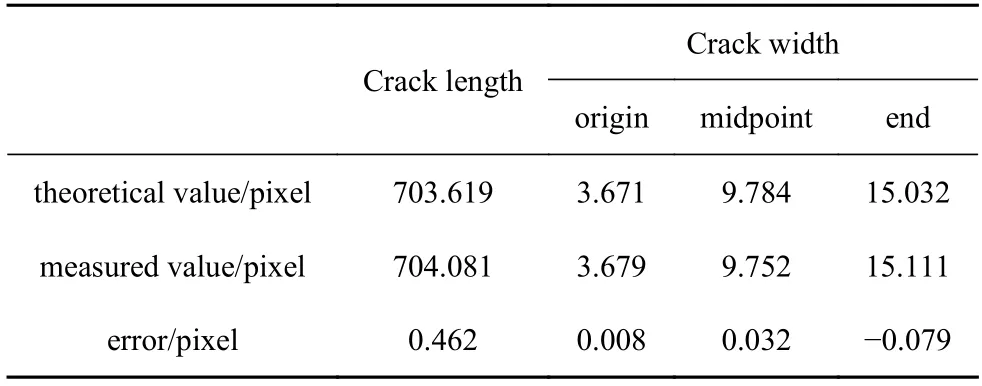
表2 裂纹尺寸测量误差Table 2 Measurement error of crack length and width

2.2 真实裂纹验证

采用德州创莱光电设备有限公司的CLHT60-AC(数显)高精度手动平移台,将两块贴合的平板彼此分离1 mm,进行等宽度裂纹的测量精度验证实验,如图9(a)所示.两块平板保持相同高度,板面喷涂散斑形成人造纹理.图9(b)为平板分离后的裂纹线性拟合结果,图9(c)为沿裂纹长度方向的裂纹宽度测量误差图,横坐标为裂纹长度方向上的等间距控制点序号(共计269 个).可以看出,采用线性拟合后的误差曲线为直线,测量总体误差在0.05 mm 以内,总体标准差为0.02 mm;直接量取得到裂纹长度真实值为52.43 mm,本文方法实测裂纹长度为52.52 mm,测量误差为0.09 mm.可见,尽管真实条件下存在多种影响因素,本文方法仍具备很高的测量 精度.

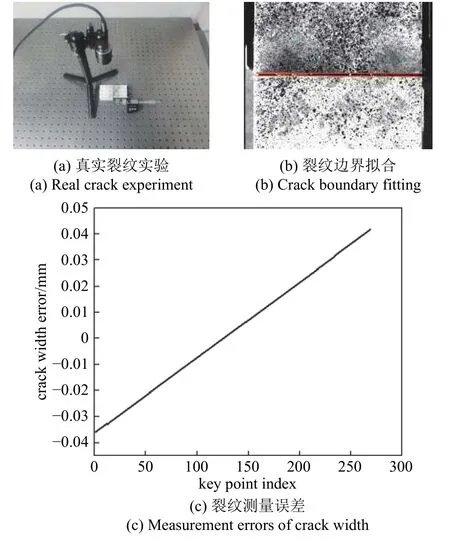
图9 真实裂纹验证Fig.9 Real crack validation

3 钢节点疲劳试验

3.1 试验概况

进一步开展十字形焊接钢节点的疲劳试验,以验证本文方法的真实有效性.设计制作两个相同的节点试件,图10 为几何构造尺寸,试件由三块钢板焊接而成,上下两块竖直钢板通过四条角焊缝焊接在水平钢板的上、下两侧,角焊缝高度6 mm,采用Q235 级钢材.在竖板端部对拉轴向力的反复作用下,焊缝位置发生疲劳开裂破坏,搭建图像采集系统并运用本文方法对疲劳裂纹的萌生及扩展全过程进行测量.

图10 焊接钢节点试件(单位:mm)Fig.10 Welded steel joints (unit:mm)

图11(a)为疲劳试验装置.试件上下端通过螺栓孔分别与疲劳试验机和刚性底座相连,刚性底座直接固定在地槽上.疲劳试验机施加的循环荷载为50～350 kN,加载频率为2 Hz.为确保得到足够的动态图像数据,采用20 Hz 的频率进行图像采集.

图11 钢节点疲劳试验Fig.11 Fatigue test of steel joints

试验前,在角焊缝等潜在开裂区域制备人造散斑,以提升DIC 计算的精度,DIC 子区尺寸取为31 ×31 像素.如图11(b)所示,该随机散斑由速干墨汁高压喷涂而成.由于每个试件存在四条焊缝且具有对称性,无法事先预见疲劳裂纹的萌生位置,因此试验全程采用四台工业相机分别对每条焊缝周边区域进行图像采集,见图11(a).工业相机分辨率为400 万像素,镜头焦距为25 mm.每台工业相机均进行了内参标定与畸变矫正.由于裂纹出现在板件主平面之上,本实验实际上为平面裂纹测量,同时采用斜对拍摄的方式进行相机架设,并基于二维单应性矩阵标定方法进行单目相机标定.

3.2 测量结果分析

试件的疲劳开裂过程重构结果及最终破坏模态如图12 所示.其中1 号试件的疲劳裂纹位于角焊缝上,2 号试件的疲劳裂纹沿角焊缝焊趾开展.初始裂纹均从试件边缘的焊缝端部萌生,随后逐渐向试件中部扩展,直至裂纹长度达到试件宽度的约二分之一(1 号试件)和三分之一(2 号试件)时发生断裂破坏.由于试件初始缺陷及荷载偏心等影响,试件实际上并非理想的对称受力,当某个角焊缝位置率先出现疲劳裂纹后,进一步加剧了这种受力不对称性,从而导致该条裂纹沿角焊缝长度方向持续扩展,而其他部位并无新裂纹产生,裂纹对侧的角焊缝仅在试件断裂前瞬间发生开裂并极速扩展至断裂.因此,每个试件仅给出这条主裂纹的测量数据.

图12 钢节点疲劳裂纹扩展过程及其重构结果Fig.12 Fatigue cracking process of steel joints and reconstruction results

通过对每一帧图像的裂纹连续边界进行曲线积分,可得到不同时刻的裂纹长度值,其随时间的增长过程如图13 所示.可以看出,两个试件的疲劳裂纹长度扩展规律大致相同,裂纹长度随荷载作用次数增加而呈现阶梯式增长,并且在开裂后期的增长速率明显高于开裂前期.

图13 实测裂纹长度时程曲线Fig.13 Time variations of measured crack lengths

图14 为裂纹萌生位置(即裂纹宽度最大处)的裂纹宽度测量结果.该裂纹宽度通过追踪一对生点的相对距离变化值得到,这两个生点分别位于上下两条离散生灭边界上,且两点连线方向垂直于裂纹长度方向,裂纹宽度值取为两点实时距离减去试验开始时的两点初始距离.可以看到,2 号试件裂纹萌生时的实测宽度仅为0.016 mm,而1 号试件裂纹萌生较为突然(初始裂纹宽度达0.081 mm),这可能与焊缝端部初始缺陷有关.在开裂初期,两个试件的裂纹宽度随加载次数增加呈现较为稳定的近似线性增大趋势,随后从某个时刻开始,裂纹宽度出现骤增,并很快发展至试件断裂破坏.基于试验相机的性能参数,采用本文方法的裂纹宽度测量精度达到了微米级.需要说明的是,裂纹宽度计算除了采用这种追踪目标点相对距离的方法外,还可基于拟合得到的上下边界曲线方程进行求解,对其实现算法不再赘述.

图14 中的散点包络线组成了裂纹宽度的上限值和下限值,上下包络线之间的差值即代表不同时刻在相同荷载幅作用下的裂纹宽度开合量,可反映十字形节点试件在疲劳加载过程中的竖向刚度变化情况.将裂纹宽度开合量以无载状态(即各个循环周期内荷载值为零的时刻)为零值进行归一处理后绘于图15,可以看出,焊缝端部的裂纹宽度开合量随着加载进行而持续增大,说明随着裂纹长度不断向内扩展,十字形节点的有效受拉面积持续减小,试件刚度不断降低.需要说明的是,本文方法通过裂纹宽度的动态开合响应进行裂纹宽度变化量的全时程测量,因此实测的裂纹宽度分辨率即为DIC 位移测量分辨率(0.01 像素).

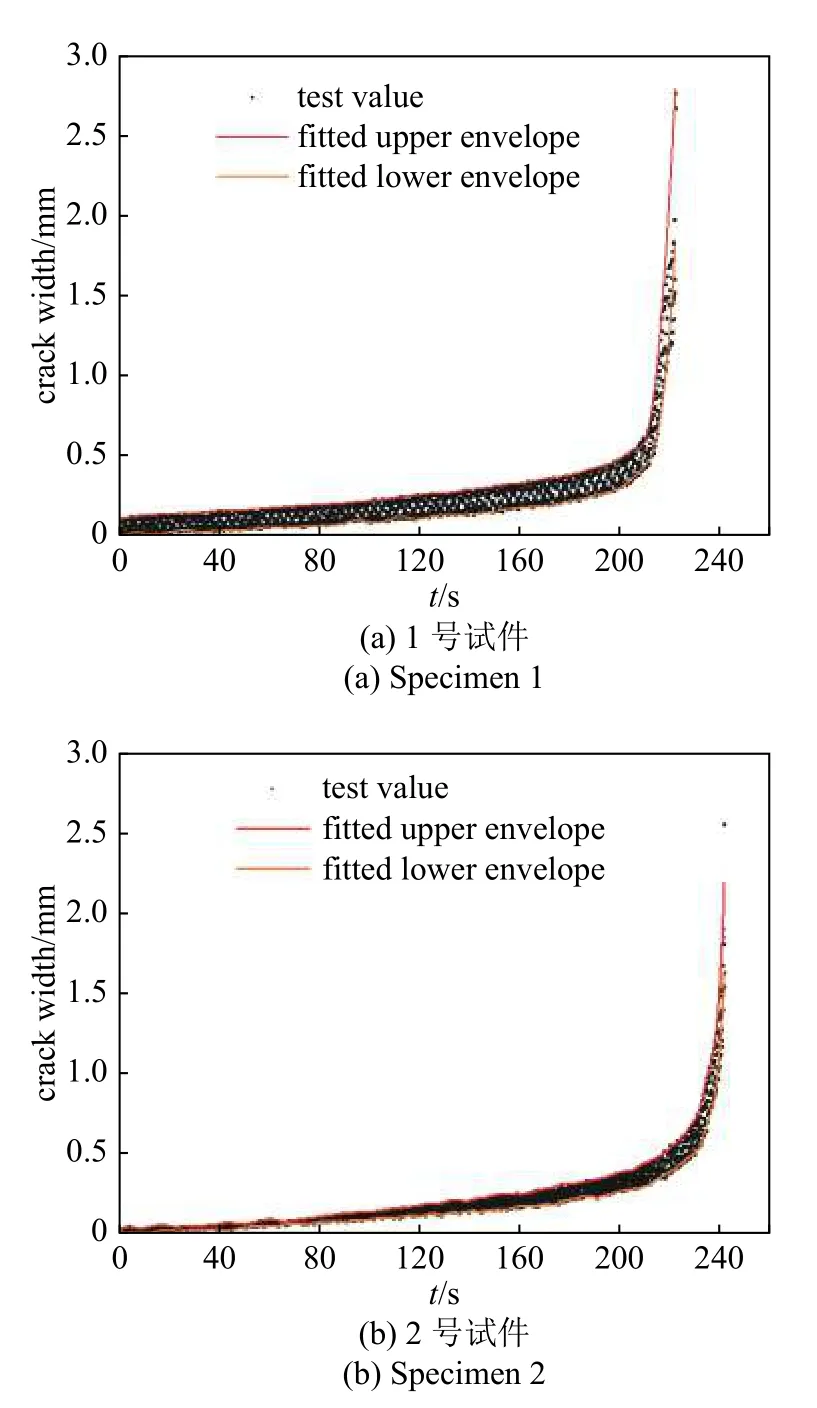
图14 实测裂纹宽度时程曲线Fig.14 Time variations of measured crack widths

图15 裂纹宽度开合量随时间变化曲线Fig.15 Time variations of measured crack folding widths

4 结论

本文运用数字图像退相关效应,提出了一种基于DIC 的疲劳裂纹全局动态测量方法.该方法通过对裂纹图像进行目标点云计算、拓扑位移场生成、裂纹灭点剔除、裂纹离散边界提取、裂纹连续边界拟合等主要步骤,完成对疲劳裂纹形态的数字化重构,并计算得到裂纹长度和宽度的量化变化过程,从而实现对疲劳裂纹动态扩展过程的精细化智能测量.

通过开展数值模拟和钢节点疲劳试验,验证了方法的准确性和有效性.结果表明:采用本文方法得到的疲劳裂纹边界重构误差小于0.5 个像素,裂纹长度和宽度计算误差分别在0.5 和0.1 像素(相当于0.06 mm 和0.01 mm)以内,并在疲劳试验过程中实现了对疲劳裂纹动态扩展过程的精准自动测量.与现有疲劳裂纹检测测量方法相比,本文方法在测量精度、效率及成本等方面均具有显著优势,可在实验室测量和工程现场测试中推广应用.