SBFEM 与非局部宏微观损伤模型相结合的准脆性材料开裂模拟1)
2022-06-13杜成斌黄文仓江守燕
杜成斌 黄文仓 江守燕
(河海大学力学与材料学院,南京 211100)
引言
混凝土是一种典型的准脆性材料,被广泛应用于土木和水利工程中.混凝土结构的破坏通常是内部微裂纹的萌生、发展贯通、形成宏观裂纹并扩展而引起结构失效的过程[1].因此,研究混凝土结构中裂纹的产生和扩展的过程至关重要.自20 世纪20年代开始,科研工作者们对固体材料破坏机理进行了大量深入研究,断裂力学[2-4]与损伤力学[5-7]得到了快速发展.
采用传统断裂力学方法时需要在断裂过程区划分足够细的网格,才能保证应力强度因子计算的准确性,且在模拟裂纹扩展时需要复杂的网格重划分[8],导致计算难度增大、效率降低.而采用传统损伤力学进行裂纹模拟时,仅需要在损伤过程区进行网格加密,无需复杂的网格重划分.损伤局部带的模拟一直是计算力学研究的热点.但传统的局部损伤模型会引起应变局部化,表现出明显的网格敏感性[9].为了弥补局部模型的不足,非局部模型[9-11]逐渐发展起来.这些非局部模型使用非局部变量作为损伤驱动变量,一定程度上减轻了网格敏感性,但在非局部变量的正则化过程中容易产生错误的结果,导致不切实际的损伤启动与扩展[12-13].并且一些非局部公式在软化阶段会不可避免地出现应力锁死的问题[14],即在损伤区域两侧出现不该有的应力传递.
近期,文献[15-16]受近场动力学[17]基本思想与统一相场模型[18-19]的启发,提出了一种非局部宏微观损伤模型.该模型引入物质点对的概念,用物质点对之间的物质键变形来定义微细观损伤,而宏观尺度上的拓扑损伤是由一定范围内微细观损伤的累积引起的.通过引入能量退化函数,将拓扑损伤嵌入损伤力学的本构关系中.该损伤模型不存在网格敏感性与应力锁死的问题[15],为准脆性材料的开裂模拟提供了一种新思路.文献[15]是在有限元框架下计算的,为了保证拓扑损伤的计算精度,需要在损伤过程区划分足够精细的网格,这导致划分网格与数值计算的时间成本大大增加.因此,采用更高效的网格划分方案与数值计算方法是非常有必要的.
比例边界有限元法(scaled boundary finite element method,SBFEM)是由Song 和Wolf[20]提出的一种新型半解析数值计算方法.该方法在环向上具有有限元精度的数值解,在径向上具有解析解,在求解时需将求解域离散为一个或多个子域,且仅需采用一维线单元对每个子域的边界进行离散,使计算维度降低一维.将其与高效的四叉树网格离散技术结合,不仅避免了悬挂节点的问题,还有效提高了计算效率[21].目前,基于四叉树网格的比例边界有限元已被成功应用于动力分析[22]、裂纹扩展[23]、弹塑性[24]、非局部损伤[25-26]等问题中.但总体而言,关于比例边界有限元在损伤方面的研究还较少,有必要进一步的探索研究.
本文将比例边界有限元与非局部宏微观损伤模型相结合,充分利用比例边界有限元网格允许存在悬挂节点的优势,采用四叉树网格离散技术实现快速、高质量的多级网格划分与尺寸过渡.将四叉树网格六种单元的计算信息预先计算并存储,计算时直接调用.以子域的比例中心作为物质点,根据影响域范围内比例中心之间的相对变形,实现从物质键微细观损伤到宏观拓扑损伤的计算.通过两个典型算例,说明本文方法可用于准脆性材料的准静态开裂模拟,不存在网格敏感性问题,并有效提高了计算效率.
1 比例边界有限元法基本理论
与常规有限元法类似,比例边界有限元法在求解时需要将求解域离散为一个或多个子域,每个子域内部需要设置一个比例中心,比例中心的选取必须满足子域边界上任意点都可见的条件[27].分别对每个子域求解后,即可得到整体的数值结果.由于该方法的相关文献丰富,本文仅给出二维比例边界有限元法的关键方程,关于更详细的推导和解释,可以参考文献[21,27].
图1 所示为一比例边界有限元子域,比例中心O设置在子域的几何中心处,子域边界采用一维线单元离散.以O为原点建立局部坐标系 (ξ,η),ξ 为径向坐标,在比例中心O处 ξ=0,在边界处 ξ=1,η 为环向坐标,其取值范围为 [ -1,1] .对于子域内任意一点的笛卡尔坐标 (x,y) 与局部坐标 (ξ,η) 的变换关系为
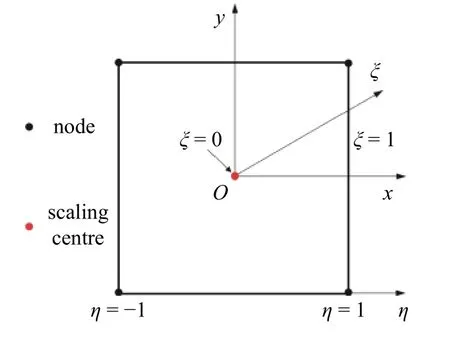
图1 比例边界有限元子域示意图Fig.1 Subdomain of a scaled boundary finite element
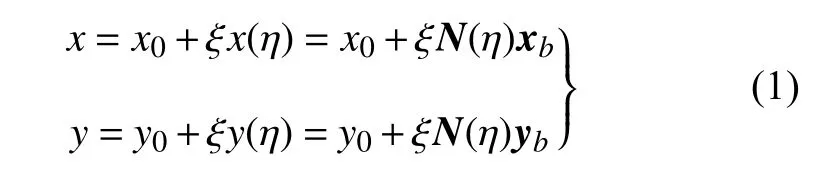
式中 (x0,y0) 为比例中心坐标,xb=[x1,x2]T与yb=[y1,y2]T为边界线单元的节点坐标,N(η) 为边界线单元的插值形函数.
子域内任意一点 (ξ,η) 的位移可以表示为
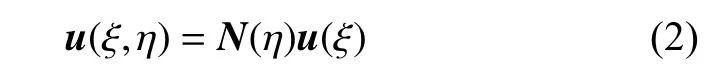
式中,u(ξ) 为径向位移函数,可以通过求解式(3)的比例边界有限元位移控制方程得到

该方程是关于 ξ 的二阶齐次微分方程.E0,E1,E2为与材料参数和几何形状有关的系数矩阵,其形式为

式中,D为弹性矩阵,|J| 为 雅克比矩阵行列式,B1(η)和B2(η)为应变位移转换矩阵,具体形式见文献[21].
式(3)为欧拉-柯西方程,可以解析求解.引入辅助变量X(ξ),可将方程转换为一阶齐次微分方程.令
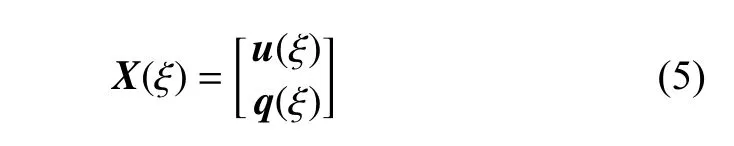
则有
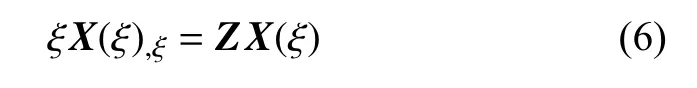
其中,q(ξ) 为与u(ξ) 对应的节点力向量,Z为Hamilton矩阵,有

将Hamilton 矩阵进行特征值分解,对于每个子域都满足下式关系
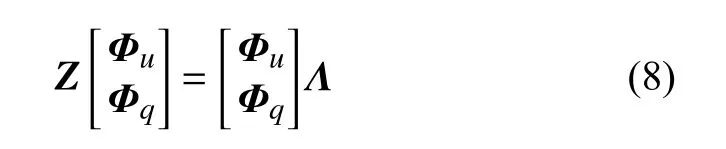
式中,Λ=diag(λ1,λ2,···,λn)为Z矩阵正特征值组成的对角矩阵,Φu=[ϕu1,ϕu2,···,ϕun] 和Φq=[ϕq1,ϕq2,···,ϕqn]分别为位移模态和应力模态,n为子域的自由度数.
通过模态叠加,式(3)所示二阶齐次微分方程的解可以表示为

其中,c为与Z矩阵特征值相对应的积分常数,可以通过子域边界节点位移ub=u(ξ=1) 求解得到

在比例中心处,只存在两种刚体位移模态[21],而刚体位移模态由第n-1 阶与第n阶位移模态控制,故在比例中心的位移可以表示为
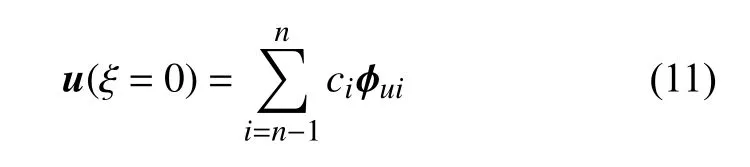
对于有界域,子域的刚度矩阵表示为[25]

对于弹性问题,将所有子域的刚度矩阵组装形成整体刚度矩阵K,得到整体平衡方程

其中,U为整体位移向量,P为整体荷载向量.
2 非局部宏微观损伤模型及其在SBFEM中的实现
非局部宏微观损伤模型是一种基于几何变形驱动的两尺度损伤模型[28],该模型结合了近场动力学中物质点对的基本思想与统一相场模型中能量退化函数的概念.为了便于理解,下面简单介绍该模型的基本概念与思想,并将其嵌入比例边界有限元的基本框架中,构建基于比例边界有限元框架的非局部宏微观损伤模型.有关非局部宏微观损伤模型更详细的介绍可参考文献[15-16].
2.1 微细观损伤与拓扑损伤
假设存在一连续体B,x与x′为B中的两个物质点.x与x′组成的物质点对记为(x,x′),物质点对(x,x′)之间建立的联系称为物质键.根据图2 所示的变形几何,可定义物质键的正伸长率为

图2 物质点对及其变形Fig.2 Deformation of material point pair

其中,ξ=x′-x为两物质点的初始空间差,u和u′分别为物质点x和x′的位移,| |•|| 表 示向量长度,〈 •〉 为麦克劳林算符,定义为 〈 α〉=max(0,α) .
当物质键的正伸长率超过材料的临界伸长率λc时,物质键开始发生不可逆的损伤,该过程与加载历史参数有关.为了表征物质键的损伤程度,引入微细观损伤函数ω∈[0,1],ω=0 表示无损状态,ω=1表示全损状态.显然 ω 是加载历史参数的函数,可取为[15]

式中,γ 为材料参数,与材料的微观结构有关,可通过标准试件试验确定.并且 γ 表征损伤发展的速度,γ的取值越大,损伤发展越快,脆性性质越明显,图3给出了不同取值的 γ 对应的微细观损伤演化曲线.加载历史参数 κ 为物质键的历史最大超越伸长率,其定义为[15-16]

图3 微细观损伤演化曲线Fig.3 Microscopical damage evolution curve

式中,t为到达当前荷载步的总时间,τ为t时刻之前某时刻所对应荷载步的时间.通常取 λc=ft/E,ft为材料抗拉强度,E为弹性模量.
从宏观上看,物质点x的损伤状态与其周围一定范围内所连接的物质键损伤有关.宏观损伤的发展代表着该点材料拓扑发生了改变[28],引入拓扑损伤函数 Ω (x) 来表征宏观损伤程度.假设物质点x的影响域半径为l,影响域表示为Dl(x) .则物质点x的拓扑损伤可定义为影响域内物质键微细观损伤的加权平均[15]

式中,影响域半径l与材料的内禀特征长度有关[9],而内禀特征长度与材料的不均匀性相关(如骨料分布、骨料最大粒径),可通过试验来确定.φ (x,x′) 为权函数,应满足非负性、定域性、归一性[17].在本文中,取权函数为
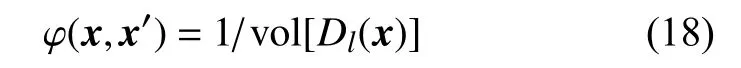
式中,v ol[•] 表示体积测度.
后面算例表明,与常规的积分型非局部模型方法相比,本文的损伤模型计算可得到更准确的局部开裂损伤带,结果更为合理.
2.2 能量退化函数
物质键发生损伤而引起拓扑损伤发展的同时,还伴随着能量耗散.引入表征物质点储能能力退化的能量退化因子[29]g,显然g与拓扑损伤的发展程度有关,因此g是拓扑损伤的函数,记作能量退化函数g=g(Ω).g(Ω) 应满足g(0)=1,g(1)=0,由于损伤总是耗能的,则 dg(Ω)/dΩ ≤0 .对于经典的连续介质损伤力学,g为 1 -Ω 的形式[5].应当指出能量退化函数g(Ω) 是区间 [ 0,1] 上的凸函数,其定性的物理解释可参考文献[15].在统一相场模型[18]的能量退化函数的基础上,采用两参数的有理分式作为非局部宏微观损伤模型中的能量退化函数[15],其形式为
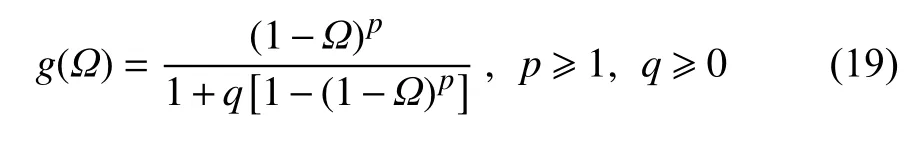
式中,p和q均为退化参数,其取值刻画了材料的宏观脆性程度,可以认为是材料的物性参数,可以通过标准试件试验确定[16,30].
2.3 非局部宏微观损伤模型在SBFEM 中的实现
如图4 所示,在比例边界有限元中,以子域的比例中心作为物质点.首先根据式(11)计算比例中心的位移,从而通过式(14)计算比例中心之间所连物质键的正伸长率,再根据式(15)对各物质键的微细观损伤进行评估,最后通过式(17)对影响域内物质键的微细观损伤进行加权平均得到拓扑损伤.如果在损伤过程区使用足够小的子域,可假定损伤在一个子域内是均匀分布的,即该子域的损伤程度可由该子域内的物质点所计算的拓扑损伤值来表征.在经典的连续介质损伤力学中,本构关系为[5]
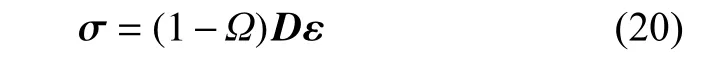
其中,σ 为应力张量,ε 为应变张量.在非局部宏微观损伤模型中,通过能量退化函数g=g(Ω) 的引入,建立起拓扑损伤与应力应变之间的联系,则本构关系转变为
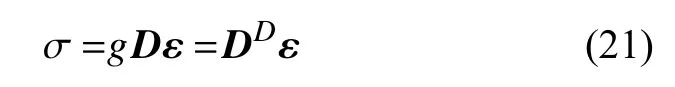
式中,DD=gD为弹性损伤矩阵,将其代入式(4),可得到子域在损伤状态下的系数矩阵

将式(22)代入式(7)的Z矩阵中,根据矩阵的性质,相应的特征值、位移模态和应力模态显然与无损状态下相同.再将式(22)代入式(12),得到子域在损伤状态下的刚度矩阵
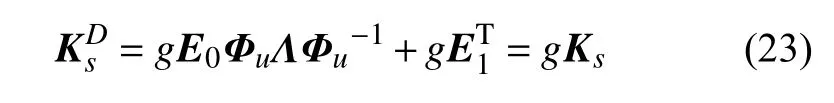
在损伤计算过程中,将所有的子域刚度矩阵进行组装,即可得到损伤状态下的整体平衡方程

其中,KD为损伤状态下的整体刚度矩阵.该方程为非线性方程,可以通过牛顿法、拟牛顿法、显式迭代法、弧长法等方法求解.在本文中,由于下降段是裂纹模拟过程中的重要阶段,故采用弧长法进行求解,关于弧长法的具体概念与公式可参考文献[31].
3 四叉树网格
四叉树是一种被广泛使用的高效分层数据结构,特别适用于网格的快速划分与网格尺寸快速平滑过渡.利用四叉树离散技术,可以高效、高质量地建立起数值计算的多级网格模型.但在不同尺寸四叉树网格之间存在悬挂节点,对于常规有限元无法直接使用四叉树网格进行计算,通常需要对网格进行特殊处理.而SBFEM 可以将悬挂节点所在边界视为两个线单元,作为多边形子域进行计算,直接避免了悬挂节点的问题.
当四叉树网格严格遵循2:1 的规则时,即相邻网格的尺寸比最大不能超过2:1,称该种网格为平衡四叉树网格.图5 为一简单平衡四叉树网格划分示意图,划分网格的基本思想是将二维结构离散为若干个正方形子网格,再对子网格重复递归离散,达到尺寸要求后方可终止离散.该网格离散算法能实现不同网格尺寸层级的快速划分及平滑过渡,从米级到毫米级的网格仅需10 次递归离散(210=1024).对于各向同性材料,采用平衡四叉树网格时,只存在图6 中的6 种单元类型.根据前述,在损伤计算过程中,SBFEM 子域的特征值、位移模态、应力模态是不变的,且每一荷载步子域的刚度矩阵都可从初始刚度矩阵计算得到,只有积分常数c需要根据每一步的位移场进行计算更新.将上述6 种单元类型的单元计算信息(特征值、位移模态、初始刚度矩阵等)预先计算并存储,在计算时可直接调用,有利于节省计算时间.故将SBFEM 与四叉树网格结合进行数值计算时,不仅使前处理阶段变得方便省时,还有效地提高了计算效率.
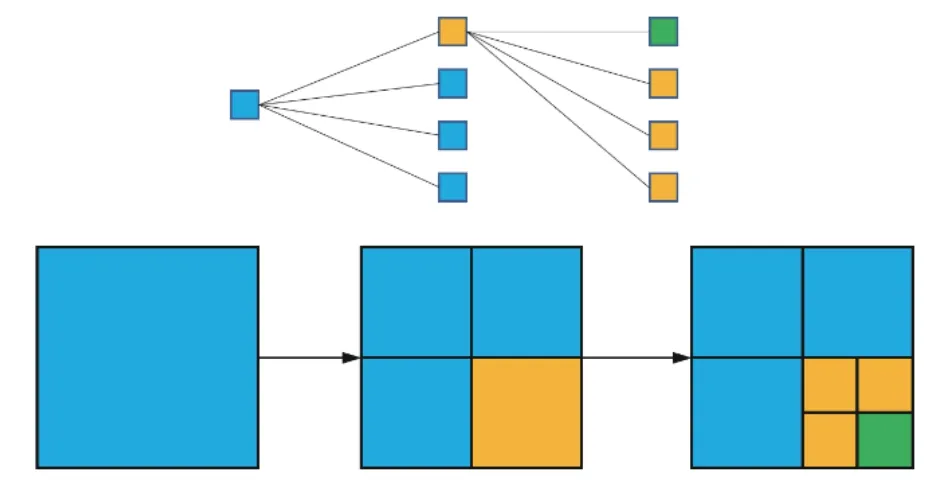
图5 平衡四叉树网格划分示意图Fig.5 Balanced quadtree discretization process
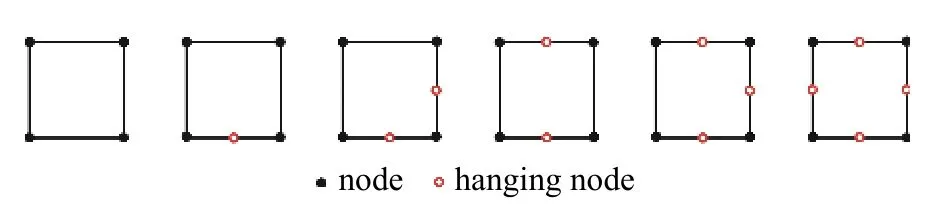
图6 平衡四叉树网格的6 种单元类型Fig.6 The six cell types of the balanced quadtree mesh
4 数值算例
本文通过两个典型试件的准静态开裂模拟,并与试验结果和其他文献结果进行比较,以此验证本文方法的正确性与有效性.为了充分说明本文方法在计算效率上的提升,使用配备Intel (R) Core (TM)i5-4200 H CPU @ 2.80 GHz 的计算机进行计算,该处理器的性能与文献[15] 所采用的Intel (R) Core(TM) i5-4210 M CPU @ 2.60 GH 接近.对于大部分模型,损伤只会出现在易损的局部区域内,同时也为了保证式(17)的数值积分精度,因此只需在损伤过程区划分足够精细的网格,其余部分的网格满足精度要求即可.所有算例均考虑为平面应力问题.
4.1 预制缺口三点弯曲梁
图7 所示为一预制缺口三点弯曲梁,其几何尺寸、边界条件和荷载信息如图所示.该算例属于张开型失效破坏,Rots[32]对该梁进行了相关试验研究.材料参数根据文献[32]选取,弹性模量E=20 GPa,泊松比v=0.2.非局部宏微观损伤模型中的参数根据文献[15]选取,影响域半径l=5 mm,临界伸长率λc=1.2 × 10-4,γ=1000,p=3,q=4.划分网格时,对缺口附近一定范围内的区域进行网格加密处理.为了研究网格敏感性问题,采用如图8 所示3 种不同疏密程度的四叉树网格进行计算.3 种网格在损伤过程区的网格尺寸均小于l/5,表1 给出了3 种网格的具体信息.
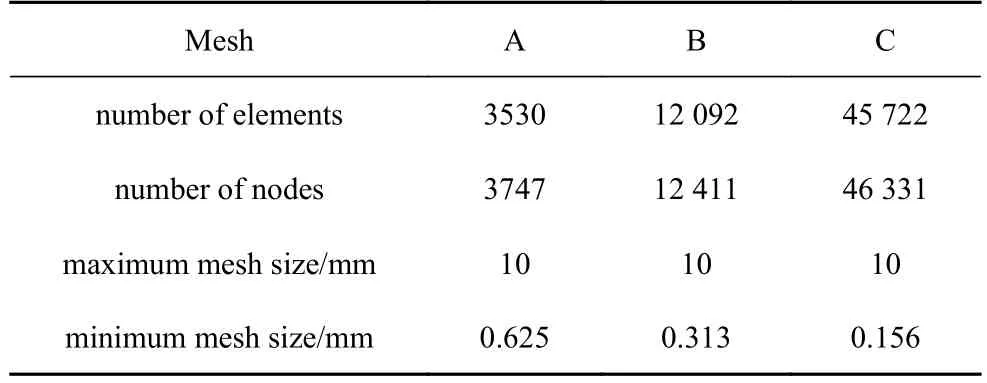
表1 预制缺口三点弯曲梁网格信息Table 1 Mesh information of the notched beam
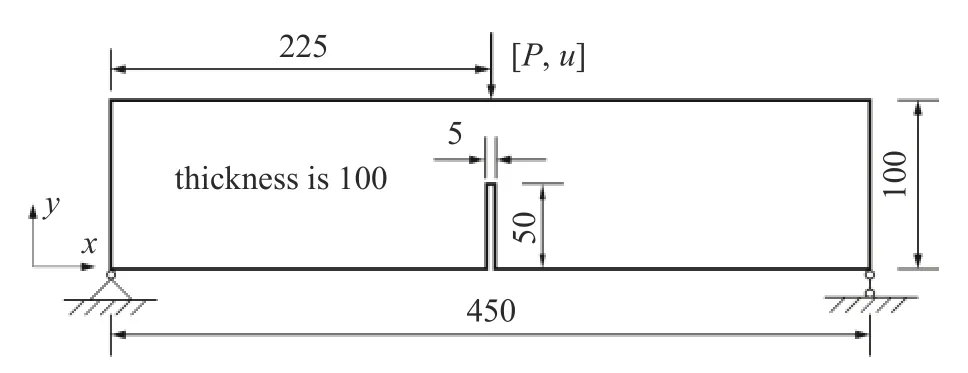
图7 预制缺口三点弯曲梁(单位:mm)Fig.7 Three-point bending of the notched beam (unit:mm)
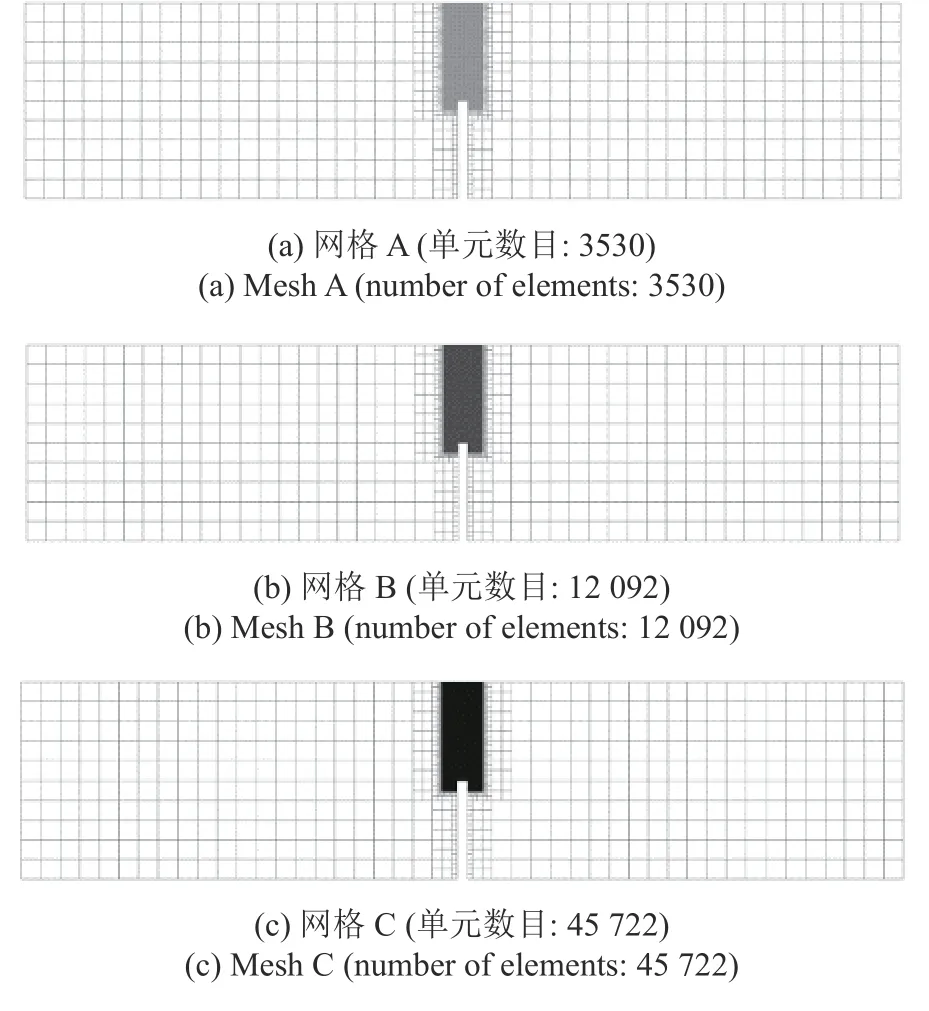
图8 预制缺口三点弯曲梁四叉树网格Fig.8 Quadtree mesh of a notched beam
3 种不同网格计算得到的最终损伤分布如图9(a)~图9(c)所示,可以看出不同网格的裂纹形态与走向基本相同.与文献[25]中采用的积分型非局部损伤模型所计算的损伤分布(图9(d))相比,本文的损伤分布是一条细窄带,能更形象表征裂纹形态,而文献中的损伤带明显较宽,对于裂纹形态的表征不够准确.与文献[33]中采用内聚力模型的计算结果(图9(e))相比,文献中的裂纹走向会受到网格影响,其主要原因是内聚单元是插入到单元边界的,裂纹扩展只能沿单元边界扩展,故内聚力模型的裂纹路径易受网格影响,表现出网格敏感性,而本文方法的裂纹路径基本不受网格影响.图10 给出预制缺口三点弯曲梁的荷载位移曲线,可以看出三种网格的荷载位移曲线具有良好的一致性.可见在网格尺寸小于l/5 时,本文方法能有效克服经典局部损伤力学中的网格敏感性问题.图10 还给出了与试验结果、文献计算结果的比较,本文荷载位移曲线与文献[32]的试验曲线范围基本吻合.在与其他文献的对比中,文献[25]采用的是基于SBFEM 的积分型非局部损伤模型,文献[15]采用的是基于有限元的非局部宏微观损伤模型,文献[18]采用的是统一相场模型.可以看出本文方法与其他文献中的方法都能较准确地捕捉荷载位移曲线,只是在下降段存在些许差别.
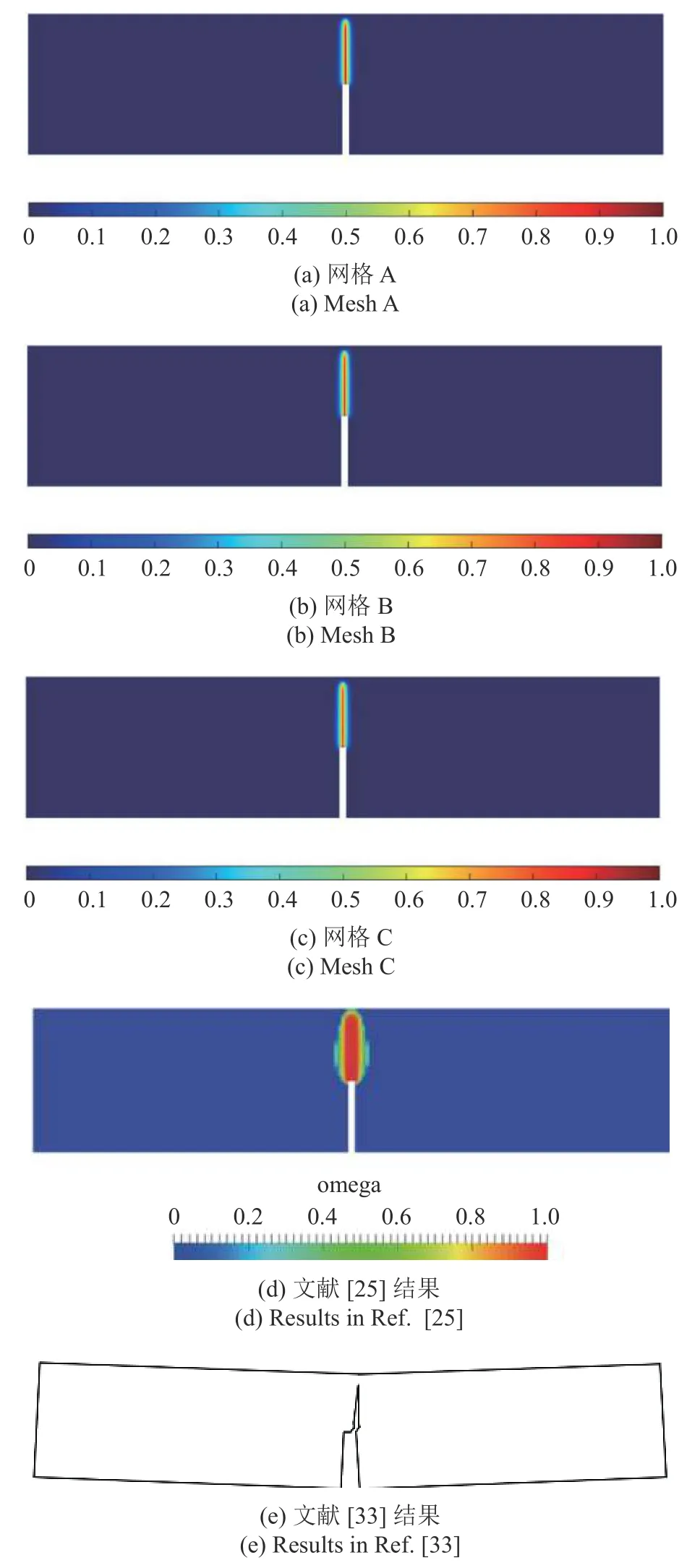
图9 预制缺口三点弯曲梁最终损伤分布云图Fig.9 Final damage distribution of three-point bending failure of the notched beam

图10 预制缺口三点弯曲梁荷载位移曲线Fig.10 Load-displacement curve for different mesh sizes
图11 给出了4 个典型阶段的损伤与位移分布云图,分别对应于图10 网格A 曲线上所标记出的四个阶段.从四个阶段的损伤分布云图可以看出,裂纹从缺口尖端开始垂直向梁顶部扩展,与在试验中观察到的现象一致.当达到峰值荷载(阶段Ⅱ)时,已经能看出较为明显的损伤,即开始出现肉眼可见的裂纹.在下降段时期(阶段Ⅱ之后),裂纹进入不稳定的发展阶段,裂纹两侧的位移场也表现出明显的不连续性.
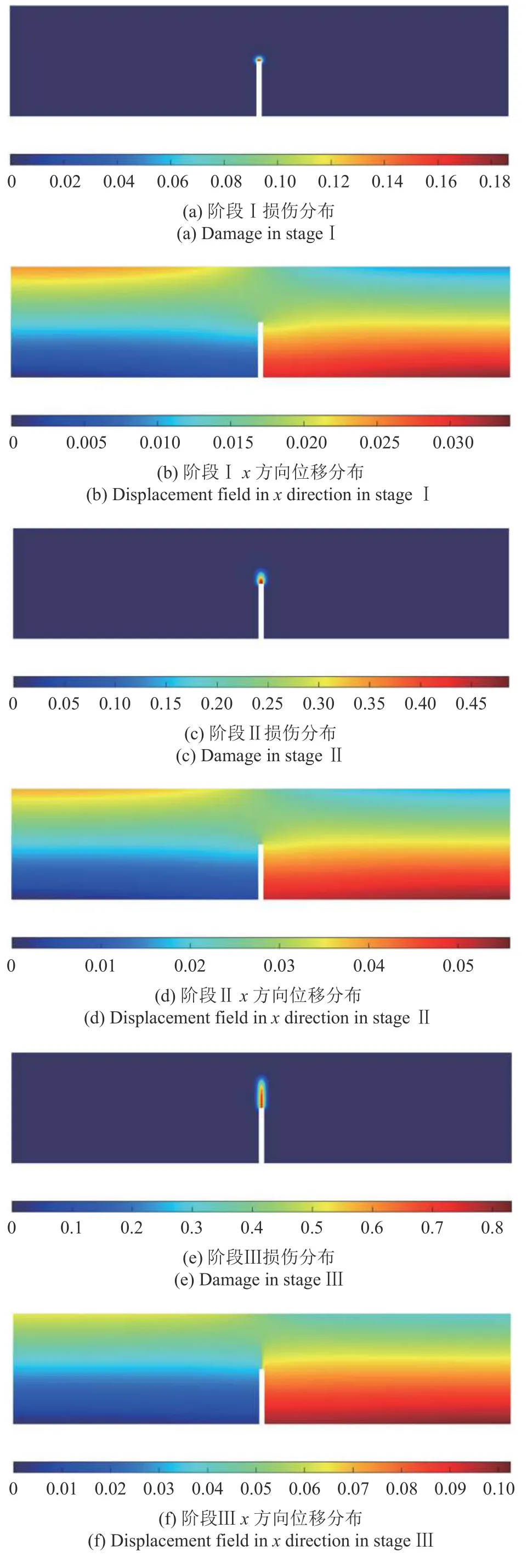

图11 预制缺口三点弯曲梁典型阶段损伤与位移分布云图 (mesh A)Fig.11 Damage and displacement field of the notched beam (mesh A)
图12 给出了网格A 裂纹附近的3 个物质点M(219.69,55.31),N(222.19,55.31),O(224.69,55.31)所连物质键在4 个典型阶段的损伤情况.从图中可以看出垂直于裂纹方向的物质键最先出现损伤,且损伤程度更大.3 个物质点是处于同一水平线上的,距离裂纹越近的点,受损的物质键越多.图13是3 个物质点的拓扑损伤发展曲线,可以看出M和N两点的拓扑损伤在阶段Ⅲ之后已趋于稳定,且损伤程度较小.是因为M和N两点只有少量垂直于裂纹方向的物质键受损,且阶段Ⅲ后这些物质键的损伤程度已达极限.而O点的拓扑损伤在阶段Ⅳ后才趋于稳定,且损伤程度已趋于完全损伤.其主要原因是O点靠近裂纹,附近的位移场具有明显的不连续性,有更多的物质键受到更大程度的损伤.从图中还可以看出,距裂纹较远的点(如M点)的拓扑损伤结果仅取决于部分方向上的物质键的损伤程度(大部分方向的物质键的损伤程度很小),计算的损伤值相对较小,从完全损伤到较小损伤过渡非常快.而常规非局部损伤模型损伤计算通过非局部变量(如等效应变或塑性应变)进行,这些非局部变量计算与所有方向上的点有关,导致非局部变量的值偏大,最终导致计算的损伤值偏大,计算的损伤带就较宽.而本文采用近场动力学的物质键失效的思路的损伤计算有别于常规有限元的损伤计算.同时,本文的损伤模型引进了统一相场的能量退化函数,使得从完好到完全损伤的过渡更为迅速.最终体现为本文方法的损伤带是一条细窄带.

图12 点M(左)、N(中)、O(右)在典型阶段的键损伤分布Fig.12 Damage of bonds of points M (left),N(middle) and O(right) in typical stage
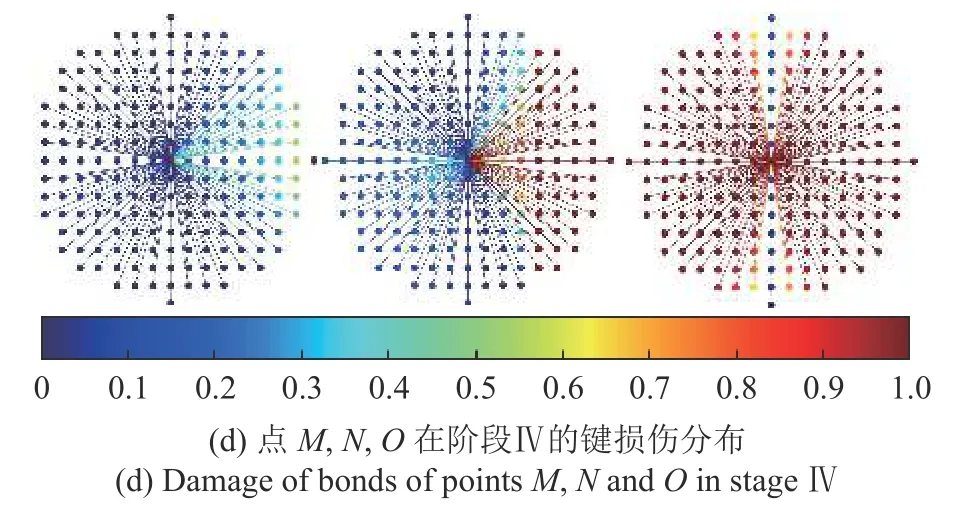
图12 点M(左)、N(中)、O(右)在典型阶段的键损伤分布(续)Fig.12 Damage of bonds of points M (left),N(middle) and O(right) in typical stage (continued)
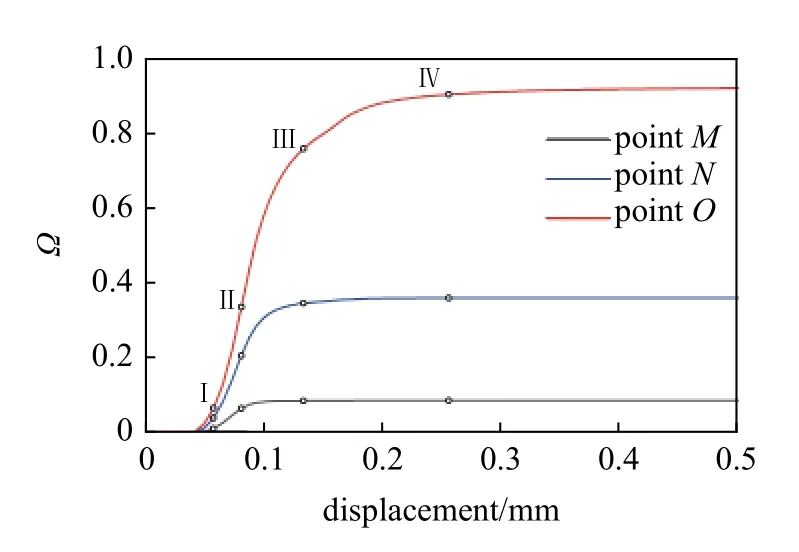
图13 点M,N,O 的拓扑损伤演化Fig.13 Topological damage evolution of points M,N and O
表2 给出了本文与文献[15]的单元数和计算时间对比,其中文献[15]采用有限元与三角形网格进行计算.因本文模型的网格A、网格B 和网格C 的计算结果几乎完全相同,以网格A 与文献[15]的网格A 比较如下,本文的单元数为3530 个,文献[15]的单元数为5712 个,这些单元主要集中在损伤过程区,前者只有后者的62%.从表中可以看出,在处理器性能与子域(单元)数相当的条件下,本文的计算时间较文献[15]大幅缩短.说明相较于常规有限元而言,将比例边界有限元与四叉树网格结合应用于非局部宏微观损伤模拟,计算效率可得到有效提高.其主要原因是四叉树网格可直接与比例边界有限元结合使用,而无需处理悬挂节点问题,且六种单元的计算信息可预先计算并存储,计算时直接调用即可,极大地提高了计算效率.
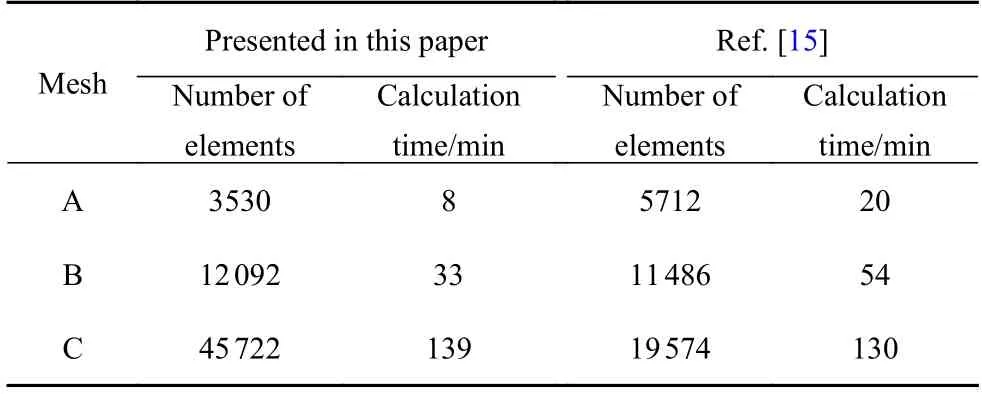
表2 本文与文献[15]的单元数和计算时间Table 2 Number of elements and calculation time in this paper are compared with Ref.[15]
4.2 L 形混凝土板
图14 为一个L 形混凝土板,其几何尺寸、边界条件和荷载信息如图所示.该算例属于混合型失效破坏,且没有预设初始缺陷,Winkler等[34]对该L 形混凝土板进行了相关试验研究.材料参数根据文献[34]选取,弹性模量E=25.85 GPa,泊松比v=0.18.非局部宏微观损伤模型中的参数根据文献[15]选取,影响域半径l=10 mm,临界伸长率λc=1.05 × 10-4,γ=850,p=4,q=4.划分网格时,对折角处至左自由边界一定范围内的区域进行网格加密处理.为了研究网格敏感性问题,采用如图15 所示3 种不同疏密程度的四叉树网格进行计算.3 种网格在损伤过程区的网格尺寸均小于l/5,表3 给出了3 种网格的具体信息.

图14 L 形混凝土板(单位:mm)Fig.14 Winkler L-shaped plane (unit:mm)

表3 L 形混凝土板网格信息Table 3 Mesh information of L-shaped plane

图15 L 形混凝土板四叉树网格Fig.15 Quadtree mesh of L-shaped plane
图16 给出了L 形混凝土板最终损伤分布与试验裂纹扩展路径,可以看出不同网格所计算的裂纹形态与走向是基本相同的,并且与试验裂纹路径吻合.图17 给出了L 形混凝土板的荷载位移曲线,可以看出三种网格的荷载位移曲线基本一致.再次说明当网格尺寸小于l/5 时,本文方法不存在网格敏感性问题.从图17 还可看出,本文荷载位移曲线基本处于文献[34]的试验曲线范围内,Winkler等[34]同时还采用基于有限元的各向同性损伤模型对裂缝开裂进行了数值模拟(图中黑色虚线).文献[15]采用的是基于有限元的非局部宏微观损伤模型,文献[18]采用的是统一相场模型.可以看出本文曲线与文献[15,34] 所计算得到的曲线差距很小,文献[18]的曲线虽然与试验曲线差距偏大,但总体趋势是正确的.

图16 L 形混凝土板最终损伤分布与试验裂纹路径Fig.16 Crack patterns (damage) for different mesh sizes
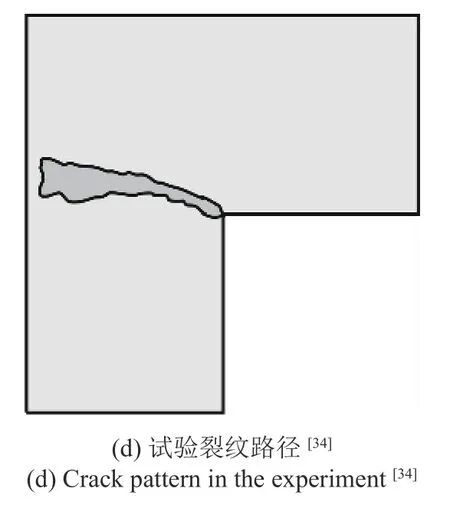
图16 L 形混凝土板最终损伤分布与试验裂纹路径(续)Fig.16 Crack patterns (damage) for different mesh sizes (continued)

图17 L 形混凝土板荷载-位移曲线Fig.17 Load-displacement curve for different mesh sizes
图18 给出了四个典型阶段的损伤分布与位移分布云图,分别对应于图17 网格A 曲线上所标记出的四个阶段.从四个阶段的损伤分布云图可以看出,裂纹起始于折角点,在向左上方扩展一段距离后,便水平向左自由边界扩展,与在试验中观察到的现象一致.类似于前述三点弯曲梁观察到的现象,L 形板在达到峰值荷载(阶段Ⅱ)时,从图18(c)~图18(d)已能观察到较为明显的裂纹.在下降段时期(阶段Ⅱ之后),裂纹两侧的位移场也表现出明显的不连续性,说明裂纹已进入不稳定的发展阶段.

图18 L 形混凝土板典型阶段损伤与位移分布云图 (mesh A)Fig.18 Damage and displacement field of the L-shaped plane (mesh A)
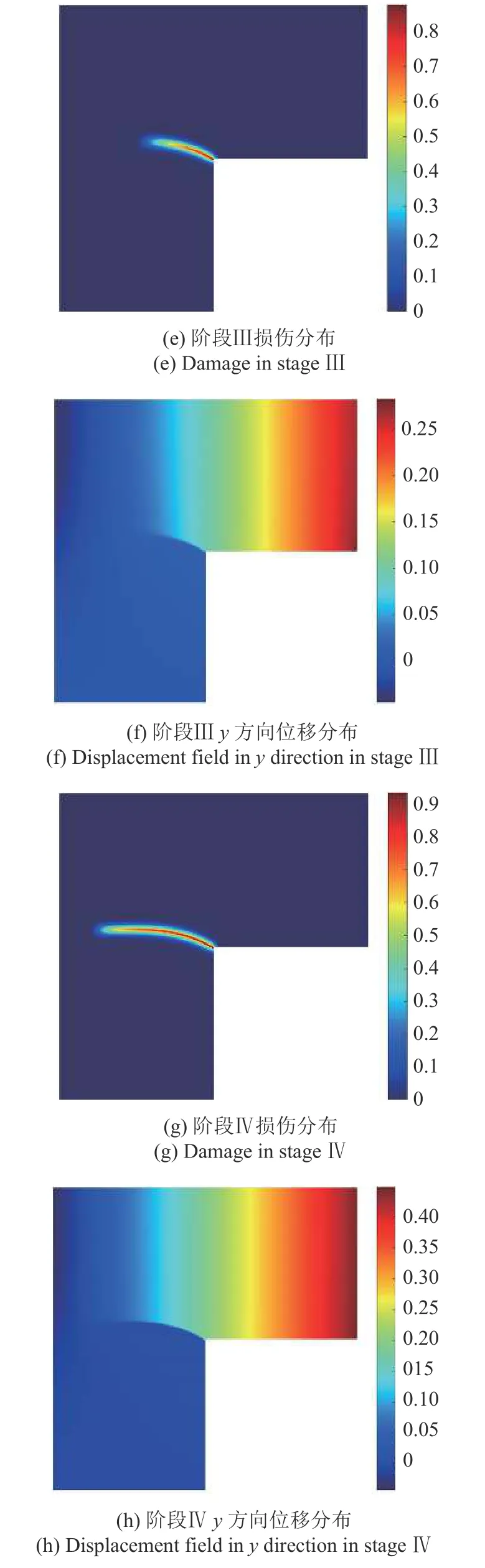
图18 L 形混凝土板典型阶段损伤与位移分布云图 (mesh A)(续)Fig.18 Damage and displacement field of the L-shaped plane (mesh A)(continued)
表4 给出了本文与文献[15]的计算单元数和计算时间的比较,其中文献[15]采用三角形单元进行计算.与前类似,选择本文模型的网格A 与文献[15]的网格A 进行比较如下,前者单元数为6396 个,后者单元数为10 902 个,前者大约为后者的59%.可以明显看出,本文的计算时间明显少于文献[15],只有后者的19%.再次说明将比例边界有限元与四叉树网格结合使用,对于提升非局部宏微观损伤模拟的计算效率是非常显著的.

表4 本文与文献[15]的单元数和计算时间Table 4 Number of element and calculation time in this paper are compared with Ref.[15]
图19 给出了网格A 裂纹附近的3 个物质点P(235.35,247.07),Q(238.35,250.98),R(235.35,254.88)所连物质键在4 个典型阶段的损伤情况.图20给出了这3 个物质点的拓扑损伤发展曲线.与前述算例类似,垂直于裂纹方向的物质键最先出现损伤,且越靠近裂纹的物质点所连物质键受损程度越大,受损的物质键数量越多,则相应的拓扑损伤也越大.且大程度的拓扑损伤集中于位移场不连续的位置,因而损伤带表现为一条细窄带.
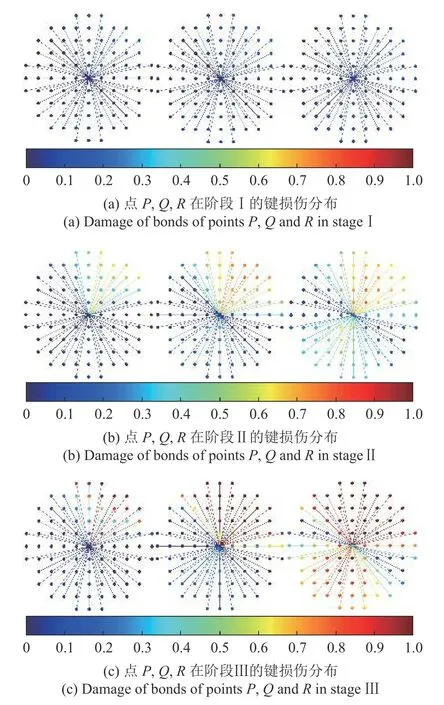
图19 点P(左)、Q(中)、R(右)在典型阶段的键损伤分布Fig.19 Damage of bonds of points P (left),Q(middle) and R(right) in typical stage
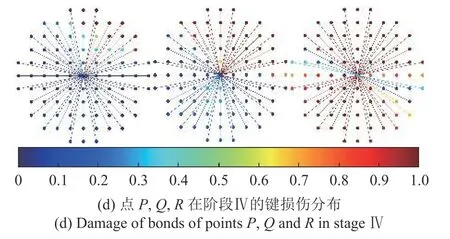
图19 点P(左)、Q(中)、R(右)在典型阶段的键损伤分布(续)Fig.19 Damage of bonds of points P (left),Q(middle) and R(right) in typical stage (continued)
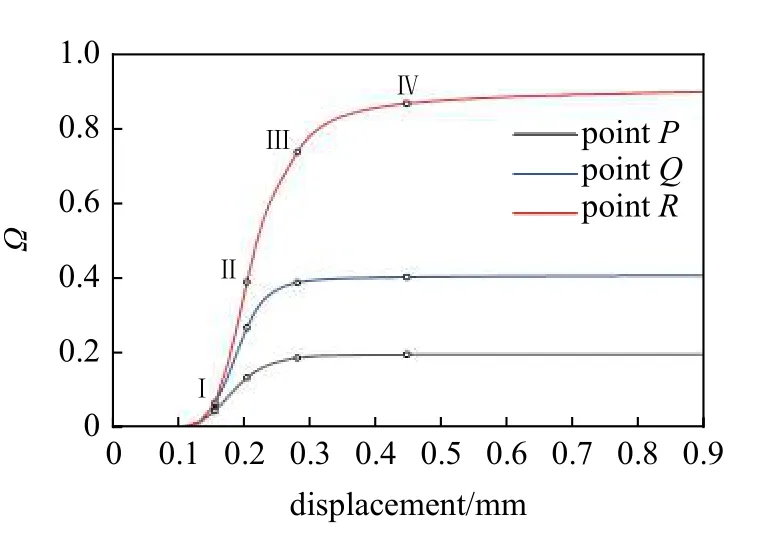
图20 点P,Q,R 的拓扑损伤演化Fig.20 Topological damage evolution of points P,Q and R
5 结论
本文将比例边界有限元与非局部宏微观损伤模型结合,采用四叉树离散技术进行网格划分,并将其应用于准脆性材料的裂纹模拟中.通过两个典型算例的验证分析,得到如下主要结论.
(1) 本文方法适用于各向同性准脆性材料的准静态开裂模拟,能准确计算裂纹扩展路径与荷载-变形曲线.对于没有预制初始缺陷的问题,裂纹的起裂与扩展也能自发进行.
(2) 本文模型是一种引入非局部思想的非局部化模型,当损伤过程区的网格尺寸小于影响域半径的1/5 时,不存在经典局部损伤力学中的网格敏感性问题.
(3) 比例边界有限元与四叉树网格结合,不存在悬挂节点问题,实现了快速、高质量的多级网格划分与尺寸过渡.六种单元类型的计算信息可预先计算并存储,有效地提高了计算效率.
本文的研究工作已初步验证了比例边界有限元与四叉树网格在非局部宏微观损伤模拟中的可行性与高效性.但还存在一系列值得深入研究的问题需要在未来解决,例如非均质材料的损伤模拟、各向异性损伤模拟、动态损伤模拟等问题.
