基于分区域虚拟材料方法的轴承结合部精确建模方法研究*
2022-06-13陈勇将汤文成郭魂华洪良
陈勇将 汤文成 郭魂 华洪良
(①常州工学院航空与机械工程学院,江苏 常州 213032;②东南大学机械工程学院,江苏 南京 211189)
滚珠轴承结合部是机床结构中最常用的一种可动结合部,主要起到承载支撑和导向定位的作用[1]。结合部模型误差是机床结构动力学建模误差的主要来源,结合部动态特性是机床动态特性的主要组成部分[2]。因此,要建立可用于机床静、动态特性分析与优化设计的机床结构数字化模型,研究滚动轴承结合部等可动结合部模型的精确构建方法至关重要。
机床结合部的数字化建模方法大致可以为两种:第一种是基于接触单元的结合部建模方法。此建模方法在有限元软件中直接通过定义接触单元来直观模拟结合部接触情况,然而,高度非线性的接触分析收敛困难,难以满足复杂机械结构的工程应用[3]。第二种是基于等效单元的结合部建模方法。此建模方法使用等效单元来模拟结合部接触情况,常用的等效单元有弹簧阻尼单元、多节点单元和虚拟材料单元。弹簧阻尼单元使用弹簧和阻尼器来等效结合部的刚度和阻尼特性,但基于此单元的建模方法仍存在弹簧单元的分布位置和数量尚无统一标准确定的问题[4-5]。多节点单元利用多节点六面体单元来等效结合部的力学特性,但此单元阻尼参数的识别尚未提出有效方法[6-7]。虚拟材料单元采用弹性模量、泊松比和密度等虚拟材料参数对结合部接触情况进行等效模拟,基于此单元的建模方法具有较高的精确性、较广的适用性和较强的实用性,近年来已广泛应用在结合部的等效建模领域[8-9]。
相较于螺栓连接固定结合部模型的虚拟材料建模研究,可动结合部的虚拟材料建模研究还很少[10-12]。廖雯俊等采用虚拟材料层对滚动直线导轨中滚柱与滚道的接触特性进行了等效模拟,将滚动直线导轨中全部滚珠简化处理成截面为正方形的圆环体作为结合部虚拟材料几何模型[13]。由此可知,已有的可动结合部虚拟材料建模方法并未考虑到滚动体与滚道接触面压力分布不均的特性,需要开展可动结合部虚拟材料模型精确建模研究,据此构建机床各类型结合部虚拟材料模型,才能建立准确的数控机床整机结构模型。
1 考虑非均匀接触特性的滚珠轴承模型构建
考虑滚珠轴承滚珠与滚道接触面间接触应力分布不均匀的特性,其结合部分区域虚拟材料模型建立的基础在于其接触面间接触应力连续变化规律的分析。滚珠轴承中不同滚珠相位角处滚珠与滚道接触应力的分布情况较难通过实验测量获得。另外,采用有限元模型通过定义接触单元来模拟滚珠与滚道接触的计算收敛困难,难以满足工程实际需要。故本文通过建立可考虑考虑非均匀接触特性的滚珠轴承理论模型,用于分析接触面间接触应力连续变化的规律。滚珠轴承中滚珠与滚道的接触,可以看作是2 个自由曲面弹性体在法向接触载荷作用下的赫兹点接触。基于赫兹接触理论可知,滚珠与滚道接触区域为椭圆形,接触应力 σ的计算公式为[14]
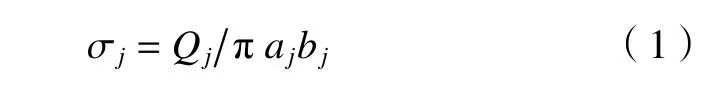
式中:j代表第j个滚珠;a为接触椭圆的长轴;b为接触椭圆的矩轴;Q为滚珠与滚道接触面间的法向接触力,其计算公式见式(2)。

式中:λ为滚珠与滚道间的法向接触变形判断因子,当 δ ≤0时,λ 为0,当 δ >0,λ 为1;kcoe为滚珠与滚道间的接触载荷变形系数;δ 为第j个滚珠与滚道间的法向接触变形,可根据变形前后外圈滚道曲率中心Oo、滚珠球心O′和内圈滚道曲率中心Oi间几何关系的变换,获得其计算公式见式(3)。
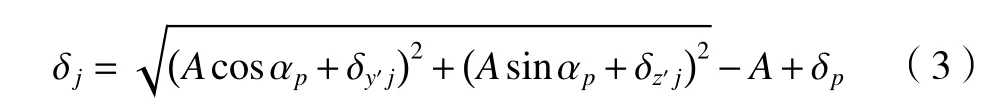
式中:A为未变形时外圈滚道与内圈滚道曲率中心之间的距离;δp为预紧载荷作用下的接触变形;αp为预紧载荷作用下的接触角;δz′和δy′为内圈滚道曲率中心移动距离在局部坐标系z′和y′轴方向的投影(图1),其值可通过绝对坐标系与局部坐标系间的微分变换式获取。
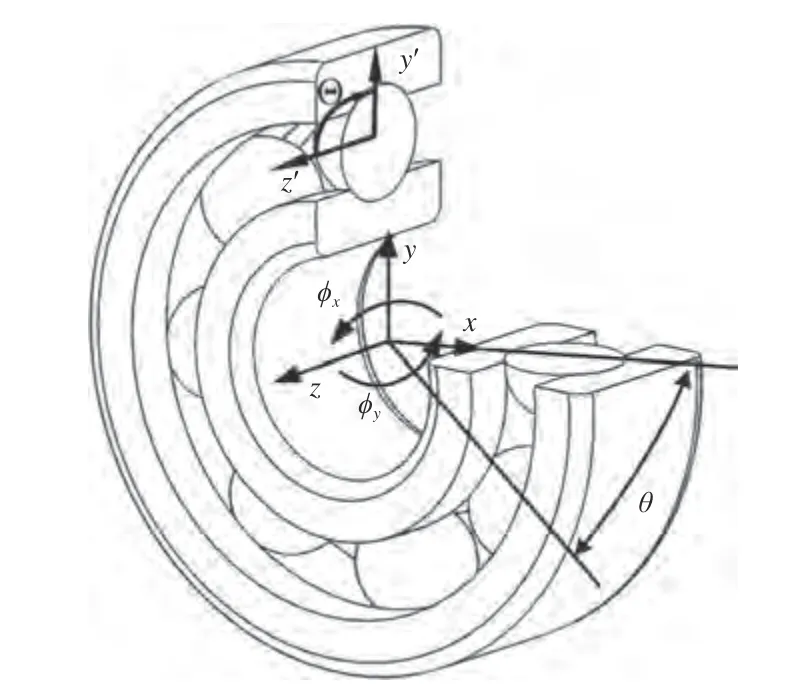
图1 滚珠轴承绝对坐标系与局部坐标系
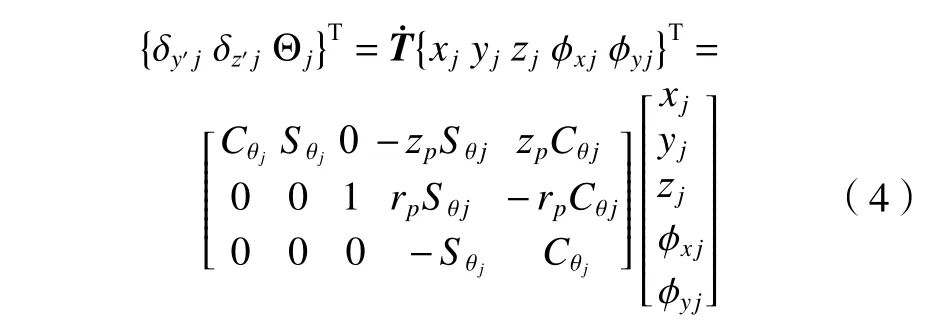
式中:θ为滚珠相位角,Sθ和Cθ分别为 sinθ 和 cosθ的简化表达式;zp和yp分别为内圈滚道几何中心至滚道曲率中心的距离在z轴和y轴方向上的投影;x、y、z、φx和φy分别为内圈滚道几何中心沿x轴、y轴和z轴方向的位移及绕x轴和y轴方向的旋转位移。
滚珠与滚道接触面间接触椭圆的长半轴和短半轴的计算公式分别为

式中:a*和b*分别为接触椭圆的长半轴和短半轴计算系数;ρ为接触点处的各个主曲率。
至此,由式(2)可求解出滚珠轴承结合部里每个滚珠与滚道接触面间法向接触力,通过力微分变换式(4)便求出内圈滚道受到所有滚珠作用的法向接触力与力矩,再利用最小二乘法来求解如式(7)所示的内圈滚道力和力矩的非线性平衡方程组,得到内圈滚道达到平衡状态时,内圈滚道最终位移值及每个相位角处的接触角和法向接触力,最终由式(1)获得所有滚珠与滚道接触面间的接触应力。

式中:a为滚珠与内圈滚道的接触角,Cα和Sα分别为 cosa和s ina的简化表达式。

式中:FX、FY和FZ分别为内圈滚道在x轴、y轴和z轴方向所受的外力,MX和MY分别为内圈滚道所受的绕x轴和y轴的力矩。
2 滚珠轴承结合部分区域虚拟材料模型建立
2.1 结合部分区域虚拟材料层几何模型
滚珠轴承中滚珠与滚道接触面间接触应力,随滚珠相位角的分布呈连续变化但规律较为复杂,采用传统虚拟材料方法建立其结合部模型已不再适合。将滚珠轴承中滚珠与保持架简化处理成截面为正方形的圆环体,在圆环体内侧和外侧即滚珠与内圈滚道接触面和滚珠与外圈滚道接触面,各取一层作为虚拟材料层,如图2 所示。基于分形理论可知其厚度为滚珠与滚道两工件微观粗糙接触表面峰底之间的距离,当表面粗糙度为0.8 μ m时,通常2 个工件微凸体层厚度值一般都在0.5 mm 上下浮动,故圆环体内、外两侧虚拟材料层的厚度h约为1 mm[10]。此几何建模方法与已有滚动直线导轨结合部虚拟材料几何建模方法相比,更全面地考虑了滚珠与内、外圈滚道的接触特性。在此几何模型基础上,再根据滚珠与滚道接触面间接触区域随滚珠相位角分布特性进行分区域,即将虚拟材料层按滚珠数量进行等分,并保证每个区域包含滚珠与滚道接触椭圆区域,使此结构材料层宏观材料特性在空间上呈现与接触应力随滚珠相位角分布相同的变化,据此能够充分表征滚珠轴承中滚珠和滚道接触面间接触应力分布不均匀的特性。
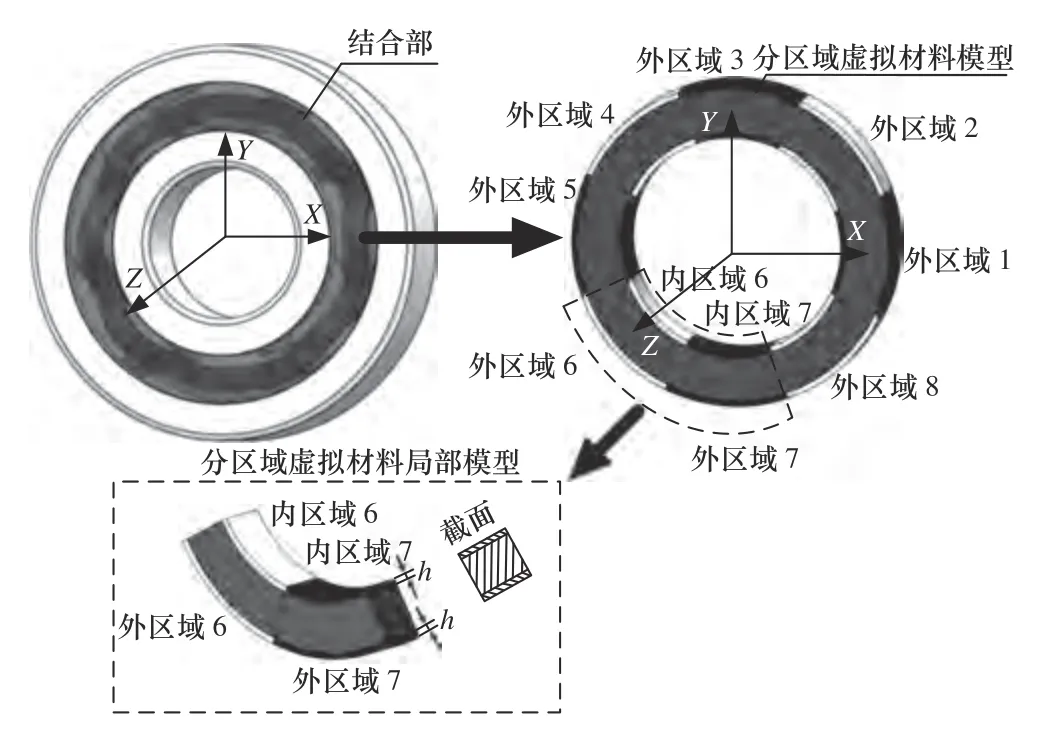
图2 含分区域虚拟材料层滚珠轴承示意模型
2.2 结合部分区域虚拟材料层参数构建
在滚珠轴承结合部分区域虚拟材料层几何模型基础上,还需构建能够表征材料属性连续不均匀分布的虚拟材料层参数。滚珠轴承结合部分区域虚拟材料层参数主要包括弹性模量、泊松比、密度和厚度。由上节可知,分区域虚拟材料层的厚度h为1 mm。为了不改变整体模型的质量分布情况,也不影响结构原有动力学特性,设置截面为正方形的圆环体质量等于滚珠与保持架质量之和。由此求出圆环体的密度,此密度值即为圆环体内、外两侧虚拟材料层的密度值。所以,还需识别的虚拟材料层参数为弹性模量和泊松比。基于已建立的可考虑非均匀接触特性的滚珠轴承模型获得的不同滚珠相位角处接触应力变化规律,建立结合部虚拟材料层的弹性模量与滚珠所处位置 θ的关系式(8),使其结构材料层的弹性模量在空间上呈现与接触应力随滚珠相位角分布相同的变化。考虑各向同性材料剪切模量G、弹性模量E和泊松比 μ间的关系,据式(8)可知,先辨识出c和m获得弹性模量,再辨识出泊松比 μ,便可唯一确定材料本构模型:

式中:c和m为待定参数;σ为滚珠与滚道接触界面间的接触应力;θ为滚珠相位角;h为虚拟材料层的厚度。
2.3 结合部分区域虚拟材料层参数获取
滚珠轴承结合部虚拟材料模型参数的辨识是精确建模的关键。由式(8)可知,辨识出c、m和泊松比 μ便可确定滚珠轴承结合部分区域虚拟材料层参数。采用多目标优化算法获得系统结合部虚拟材料模型的参数是一种有效的参数获取方法[12-13],设计变量为c、m和泊松比μ,目标函数为系统的仿真固有频率和试验固有频率之间差值的最小化,如式(9)。其中,根据模态有效质量比计算结果决定试验固有频率参与到目标函数优化过程的阶数,通过对比试验模态振型与理论模态振型的相似性,确定试验固有频率具体选择的阶数。
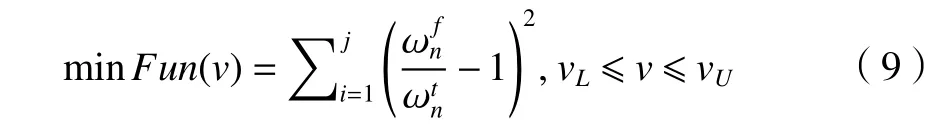
在确定了待辨识参数的优化规划区间和优化目标函数后,需要选择合适的多目标优化算法,多目标遗传算法是常用的支持多个目标优化的方法。多目标遗传算法的核心是协调各个目标函数之间的关系,寻找出各个目标函数都尽可能达到较大或较小的函数值的最优解。在众多多目标优化的遗传算法中,带精英策略的非支配排序遗传算法(NSGA-II)是目前影响较大及应用范围较广的一种多目标优化遗传算法。
3 应用案例
3.1 应用对象及含虚拟材料结合部的滚珠轴承动力学模型建立流程
选取试件尺寸和滚珠数量均不同的2 个角接触球轴承,据此可同时对2 个不同的轴承结合部进行研究,验证建模方法的通用性,滚珠轴承主要结构参数及虚拟材料层密度值见表1。基于多目标优化方法获得结合部虚拟材料层的参数,从而建立含虚拟材料结合部的滚珠轴承动力学模型,其主要流程如图3 所示,具体过程为:首先,通过式(1)获取滚珠与滚道间接触应力随滚珠相位角的分布规律,根据滚珠数量将轴承虚拟材料层划分成相应层数,每层泊松比取常数,而弹性模量结合式(8)得到相应层数其值与滚珠相位角的定量关系,从而获得待辨识参数c和m所属滚珠位置的关系式;其次,将含待辨识参数c和m的弹性模量表达式及泊松比 μ代入到含虚拟材料结合部的滚珠轴承数值模型计算得到相应的理论固有频率与振型,并通过实验采集到滚珠丝杠副的实验固有频率与振型;最后,以式(9)作为目标函数,并采用非支配排序遗传算法(NSGA-II)获取到待辨识参数最佳值,并进行实验验证,最终建立精确的含虚拟材料结合部的滚珠轴承动力学模型。
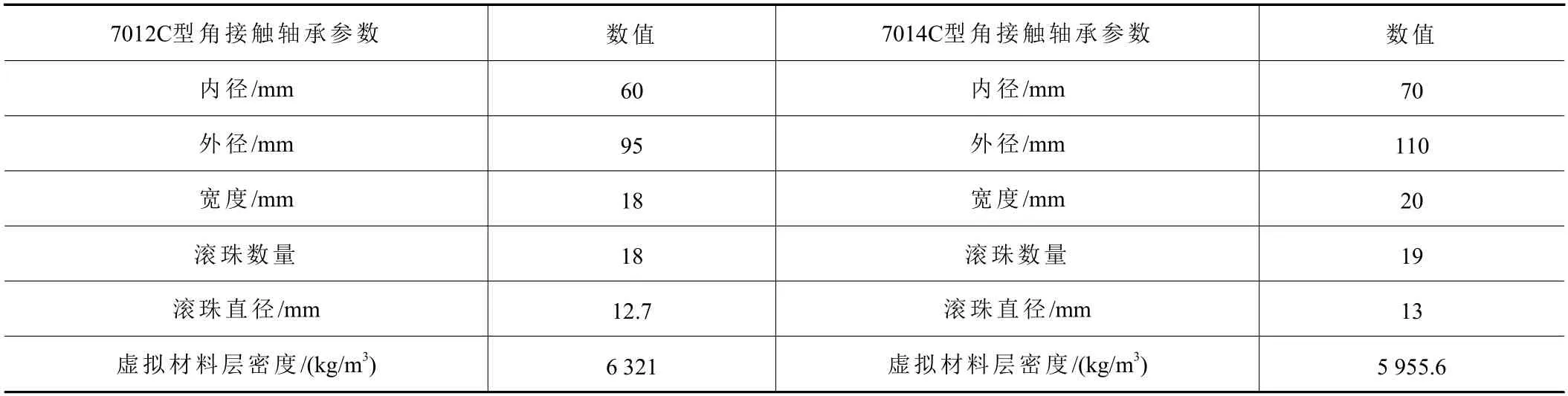
表1 滚珠轴承主要结构参数及虚拟材料层密度值

图3 含虚拟材料结合部的滚珠轴承动力学模型建立流程
3.2 实验系统设计及实验模态分析
为了验证基于虚拟材料方法建立的滚动轴承结合部动力学模型,搭建了如图4 所示的滚动轴承模态测试平台:将2 个不同尺寸的角接触轴承安装至简易主轴箱上,作为主轴的支承部件,使轴承结合部成为被测试系统的唯一结合部;测试系统主要由力锤(PBC 086C03)、加速度传感器(PCB 352C33)、数据采集装置(LMS SCM202)、实时动态分析模块(LMS TestLab 14A)以及计算机组成,其中力锤的灵敏度为2.25 mv/N、加速度计的灵敏度为99.7 mv/g。

图4 滚珠轴承模态测试平台
模态实验采用移动力锤法,传感器安装在主轴箱上,通过钢丝绳悬挂主轴箱试件来模拟自由边界条件,在试件上布置了40 个激励点。根据模态有效质量比计算结果可知,需取6 阶试验固有频率参与到目标函数的优化过程。通过对比试验模态振型与理论模态振型的相似性,确定此6 阶试验固有频率具体选择的阶数。由获得的实验振型即表2 可知:第一阶振型主要为箱体前后板异步Z方向平动;第二阶振型主要为箱体左右侧板同步Y方向平动;第三阶振型主要为箱体左右侧板同步Y方向弯曲摆动;第四阶振型主要为箱体前后板异步X方向弯曲摆动与左右两侧板同步Y方向弯曲摆动;第五阶振型主要为箱体前后板异步X方向弯曲摆动;第六阶振型主要为主轴随箱体前后板同步X向弯曲摆动。

表2 试验振型与仿真振型对比
3.3 结果与讨论
3.3.1 结合部虚拟材料模型有效性验证
由设计的实验系统可知,装配在主轴箱的2 个轴承主要在径向承受主轴的重量,轴向并未受预紧载荷作用。根据轴承结合部虚拟材料模型参数获取流程得到虚拟材料层不同区域的弹性模量与泊松比的优化值,将此参数代入含分区域虚拟材料结合部的轴承模型,可得到主轴箱系统的仿真频率。由图5 可知,基于含分区域虚拟材料结合部的轴承模型获得的仿真固有频率与实验固有频率间最小误差出现在第五阶,仅为3%;最大误差出现在第六阶,为14.78%。由此可知,基于含分区域虚拟材料结合部的轴承模型获得的仿真固有频率与实验固有频率基本吻合,仿真固有振型与实验固有振型基本一致。
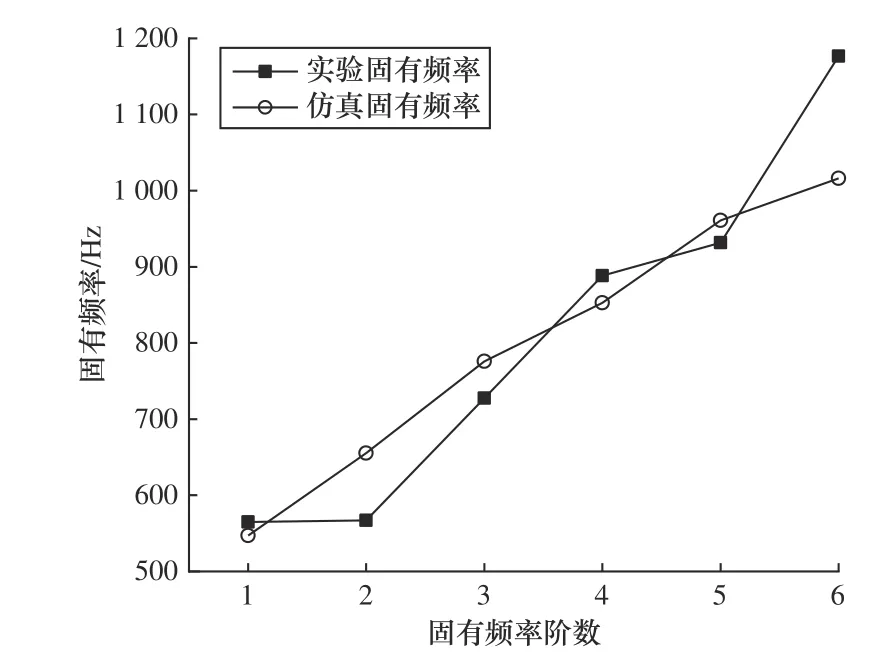
图5 实验固有频率与仿真固有频率对比
3.3.2 接触应力影响因素及其分布规律分析
由于不同预紧载荷作用下,7012C 型与7014C型角接触轴承的接触角与接触应力随滚珠相位角的分布情况相似,所以只对7012C 型角接触轴承的接触应力影响因素及其分布规律进行分析。图6 至图9为预紧载荷分别为0 N、900 N、1 200 N、1 500 N与1 800 N 时,接触角、接触载荷、接触椭圆长短轴及接触应力随滚珠相位角的分布情况。滚珠与滚道接触面上接触角的变化直接影响着两接触面几何关系,它是影响接触应力的重要几何参数,故首先对其进行分析。由图6 可知,所有相位角处滚珠与滚道的接触角随着预紧载荷的变大而减小,接触角最大与最小值分别出现在相位角80°和260°左右,相位角180°处的接触角变化最小,滚珠相位角如图1 所示参照轴为X轴。由式(1)可知,滚珠与滚道间接触载荷值直接决定了法向接触应力的大小。如图7 所示,不同滚珠相位角处接触载荷随预紧载荷增大而变大,其分布情况与接触角的分布情况有所区别。
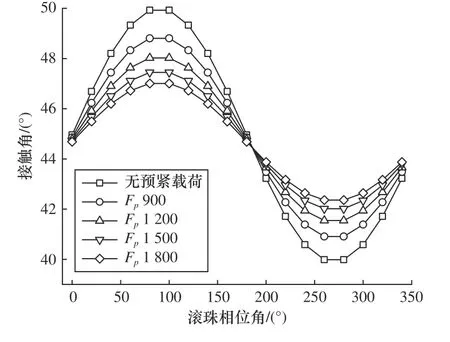
图6 接触角随滚珠相位角分布规律
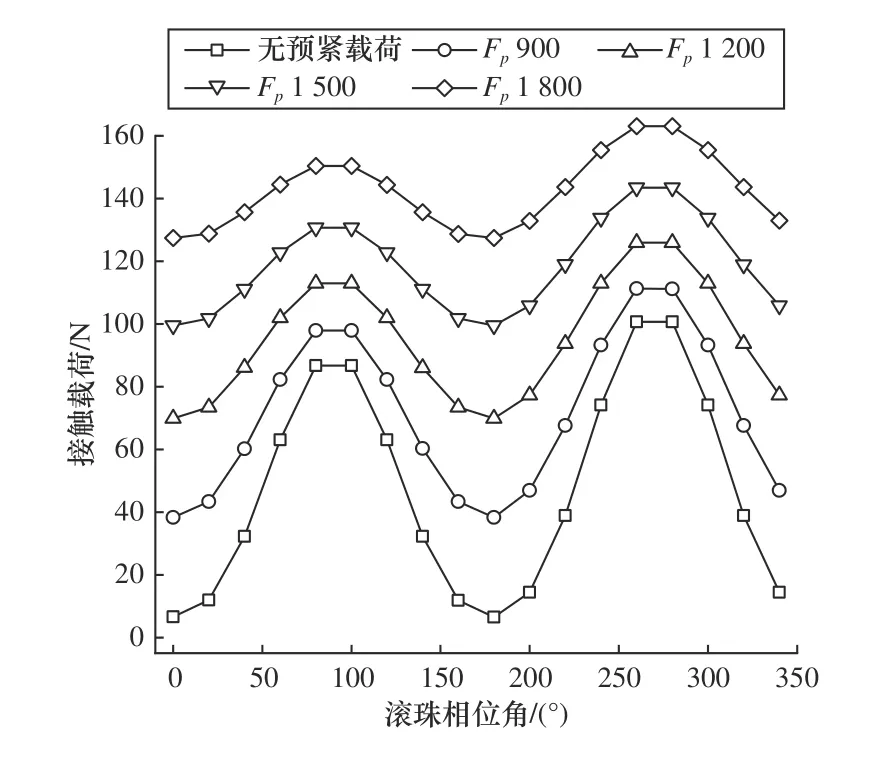
图7 接触载荷随滚珠相位角分布规律

图8 接触区域长短轴随滚珠相位角分布规律
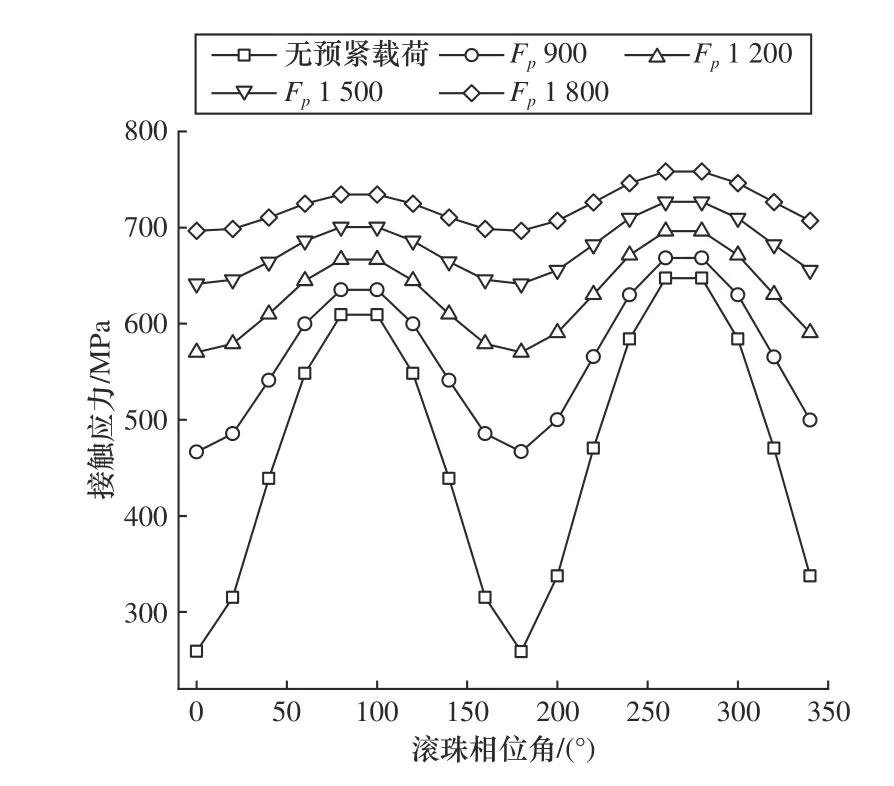
图9 接触应力随滚珠相位角分布规律
由式(1)可知,滚珠与滚道间接触椭圆的长短轴是直接决定法向接触应力大小的另一个重要参数。图8 为不同滚珠相位角处滚珠与滚道间接触椭圆的长短轴随预紧载荷改变而变化的情况,滚珠与滚道接触面上接触椭圆的短轴与长轴有类似的分布情况与变化规律,其值随预紧载荷增大而变大,其分布情况与接触载荷分布情况类似,接触椭圆长短轴大小的差异随预紧载荷增大而变小。由图9 可知,所有相位角处滚珠与滚道的接触应力随着预紧载荷的变大而增大,接触应力最大与最小值同样分别出现在相位角80°和260°左右。无论接触角、接触载荷还是接触应力的分布不均匀性趋势,都会随着预紧载荷的变大而逐渐减小。
3.3.3 虚拟材料参数对系统动态特性的影响分析
含分区域虚拟材料层的滚珠轴承模型的虚拟材料层厚度和密度值皆已确定,而弹性模量和泊松比是通过多目标优化方法获取,故主要讨论弹性模量和泊松比的改变对主轴箱系统固有频率的影响。分别取优化后弹性模量的最大值442.6 MPa 和最小值14.3 MPa,作为轴承虚拟材料层所有区域的弹性模型,获得相应的主轴系统固有频率,并与基于多目标优化获取参数的仿真固有频率进行对比。如图10所示,随着弹性模量的增大,主轴箱系统的固有频率随之变大,并从第三阶开始,它们间差异随之增大。分别取优化后泊松比的最大值0.45 和最小值0.16,作为轴承虚拟材料层所有区域的泊松比,获得相应的主轴系统固有频率,并与基于多目标优化获取参数的仿真固有频率进行对比,如图11 所示,随着泊松比的增大,主轴箱系统的固有频率也随之变大,并从第三阶开始,它们间差异也随之增大。但相较于弹性模量对主轴系统固有频率而言,泊松比的影响较小。
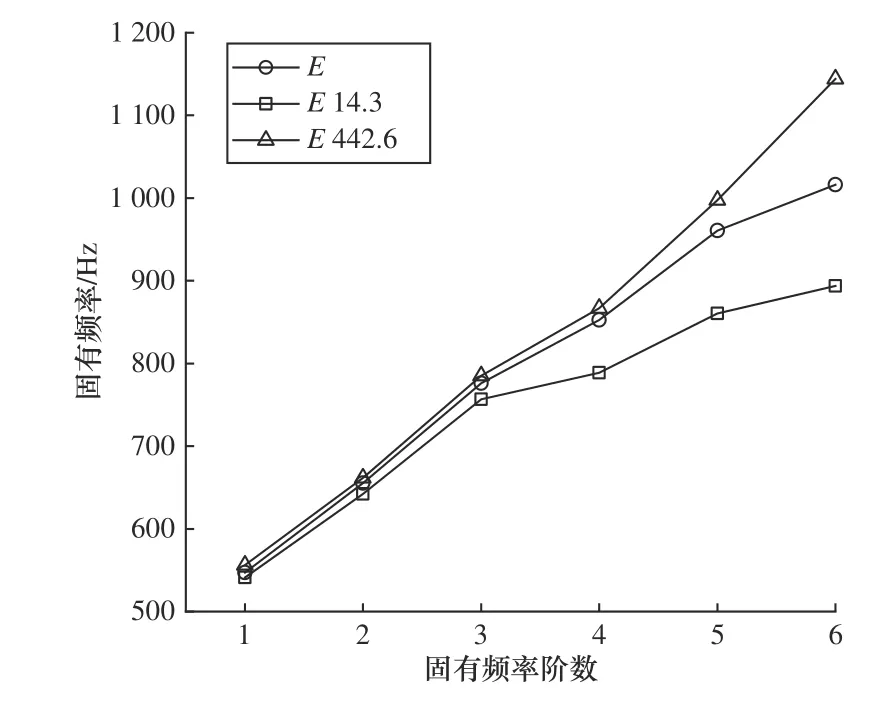
图10 弹性模量对系统固有频率的影响
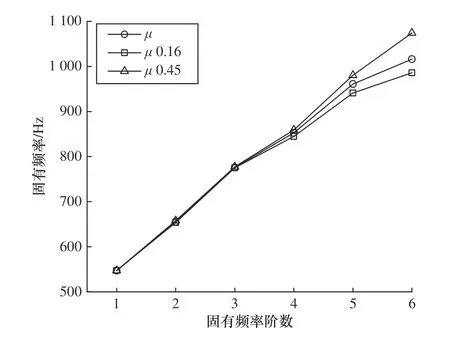
图11 泊松比对系统固有频率的影响
4 结语
(1)针对滚珠轴承中滚动体与滚道接触面压力分布不均的问题,由实验与仿真结果对比可知:提出的分区域虚拟材料结合部建模方法是一种表征滚珠与滚道接触应力分布不均特性的有效方法。该方法不会改变模型原有质量与尺寸,故应用于复杂结构时,可有效避免增加结合部模型求解的自由度数。
(2)基于建立的滚珠轴承理论模型可知:滚珠与滚道接触面上接触角的变化直接影响着两接触面几何关系,它是影响接触应力的重要几何参数;滚珠与滚道间的接触应力分布情况受接触载荷与接触区域长短轴的分布情况影响;无论接触角、接触载荷还是接触应力的分布不均匀性趋势,都会随着预紧载荷的变大而逐渐减小。
(3)含分区域虚拟材料层的滚珠轴承模型的虚拟材料层厚度和密度值皆已确定,而弹性模量和泊松比是通过多目标优化方法获取,故结合部的建模精度主要由弹性模量和泊松比这2 个参数所决定;相较于弹性模量对主轴系统固有频率而言,泊松比的影响较小。
