基于GA-BP神经网络的重庆市生活垃圾量预测模型研究
2022-06-13李宗敏
闫 芳,舒 垚,李宗敏
(1.重庆交通大学 经济与管理学院,重庆 400074;2.四川大学 商学院,四川 成都 610065)
随着城市和社会的发展,人们对城市环境卫生的要求越来越高,同时城市化和消费水平的不断提高,其带来的生活垃圾量与日俱增,对城市环境和公众健康构成严重威胁,城市垃圾管理已经成为城市发展所面临的重要环境问题[1]。重庆是我国重要的中心城市之一,是国家重要的现代制造业基地,肩负着西南地区经济发展重任,其对内的经济或对外的开放发展都需要一个清洁卫生、文明和谐的环境基础。在旅游热潮下,重庆市成为旅游地中的网红城市,剧增的垃圾量给重庆市垃圾处理带来了巨大的压力,合理科学地预测垃圾量可为垃圾处理提供可靠的决策信息,而目前对重庆市垃圾量的研究较少[2]。对于垃圾量的预测,已有很多学者进行了相关的研究,主要的预测方法包括神经网络模型[3-4]、系统动力学[5]、灰色预测[6-7]、组合预测[8]等模型,其中神经网络模型的应用较为广泛,具有预测精度高、高度自学习和自适应等能力。王晓平等[9]利用遗传算法优化后的BP神经网络预测镇农产品冷链物流需求,预测精度高,所以笔者将选取GA-BP神经网络对重庆市垃圾量进行预测。在对垃圾量进行预测时,合理地筛选影响垃圾量因素,是准确预测垃圾量的关键。于涛等[10]根据实际情况选取了非农业人口、GDP、社会消费品零售总额、城市居民人均消费性支出、城市居民人均年可支配收入5个因素作为城市生活垃圾清运量的影响因素;陈艺兰等[11]通过系统动力学理论选取户籍人口、非户籍人口、常住人口、GDP作为主要影响因素;任婉侠等[12]利用灰色关联度选取了城市建成区面积、人均公共绿地面积、市区人口数量、人均消费支出为主要影响因素;HOANG 等[13]分析了气候和社会经济因素对人工神经网络城市垃圾预测模型的影响。可见影响垃圾量的因素众多且筛选影响因素的方法多样,但同一模型不一定适用于所有的地区。因此,笔者将利用3种不同的方法进行影响因素筛选,确定主要影响因素体系,结合ARIMA模型和GA-BP网络模型对重庆市的垃圾量进行预测,旨在探究主要影响因素,提高预测精度,为重庆市实现科学合理的一体化生活垃圾管理提供数据支撑。
1 重庆市垃圾量情况
据统计,重庆市累计建成生活垃圾处理设施62座,其中实际运行的垃圾处理设施有57座(含餐厨垃圾处理厂1座,规模1 000 t/d),城区的垃圾收运设施基本配备,具有较充足的垃圾收集和处理能力。此外,城市生活垃圾清运量是建设城市生活垃圾处理工程的重要依据,故以城区垃圾清运量作为衡量重庆生活垃圾量的指标进行预测。重庆市2004—2018年城区生活垃圾清运量与年增长率如表1所示。

表1 2004—2018年重庆市垃圾清运量与年增长率
2 垃圾量的影响因素
影响垃圾量因素的筛选,是预测垃圾量的重要步骤。为了更好确定对垃圾量影响较大的因素,且使垃圾预测更准确,分别利用Lasso回归分析、灰色关联度分析、文献总结分析3种方法来筛选影响因素,然后对不同方法筛选的因素进行拟合比较,确定合适的因素。影响城市垃圾量的因素复杂多样,主要包括内在因素、自然因素、个体因素、社会因素4个方面[14]。其中,地域、自然、社会道德等不易具体考量,很难综合全面地将4个方面的因素都考虑在内,故根据已有文献及实际情况,分析了重要且可量化的重庆城市生活垃圾量影响因素,如表2所示。
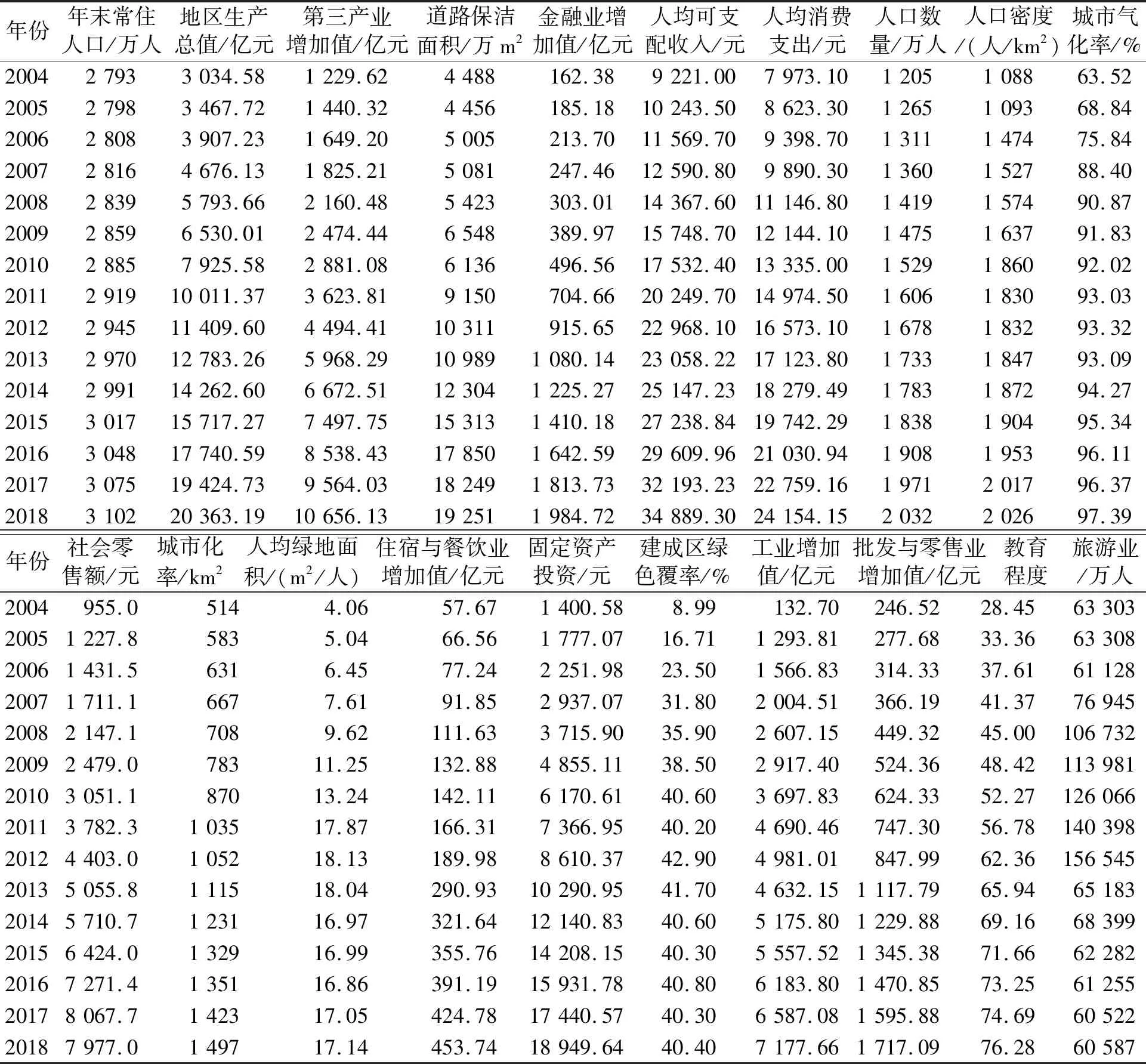
表2 各影响因素及其数据
2.1 Lasso回归分析
Lasso回归分析(Least absolute shrinkage and selection operator)的原理与多元线性回归相似,多元线性回归的回归系数使用的是OLS(最小二乘法),但变量过多时可能会导致多重共线性问题造成回归系数的不显著,甚至造成OLS估计的失效。而Lasso回归在OLS回归模型的损失函数基础上加了不同的惩罚项,而Lasso回归在OLS回归模型的损失函数基础上加了不同的惩罚项,该惩罚项由回归系数的函数构成,如式(1)所示。
(1)
式中:β为未知回归系数;X为自变量;Y为因变量;λ为惩罚系数;p为样本数。加入的惩罚项能识别出模型中不重要的变量,将不重要的变量系数压缩为0,对模型起到简化作用;且加入的惩罚项能让模型变得可估计,避免多重共线性的问题。
Lasso回归是没有显示解的,只能近似估计,利用K折交叉验证的方法来选择最佳的调整参数,使得整个MSPE最小。利用Stata软件实现Lasso回归模型,进而完成变量筛选。在回归分析前需对变量进行标准化处理,由于Stata每次只能对单个变量进行标准化处理,故利用Matlab中的Zscore函数来对数据做标准化处理。其主要代码为:CvLassoYX1X2X3X4X5X6X7X8X9X10X11X12X13X14X15X16X17X18X19X20,lopt seed(600)。其中,Y为垃圾清运量,X为各个影响因素,选择项“lopt”表示选择使MSPE最小的λ,多次调整,选择随机数种子数为600,默认为10折交叉验证。筛选出来的变量如表3所示,可知Lasso回归分析最终选出的变量为:X4道路清扫保洁面积、X5金融业增加值、X10城市气化率、X11社会零售额、X13人均绿地面积。
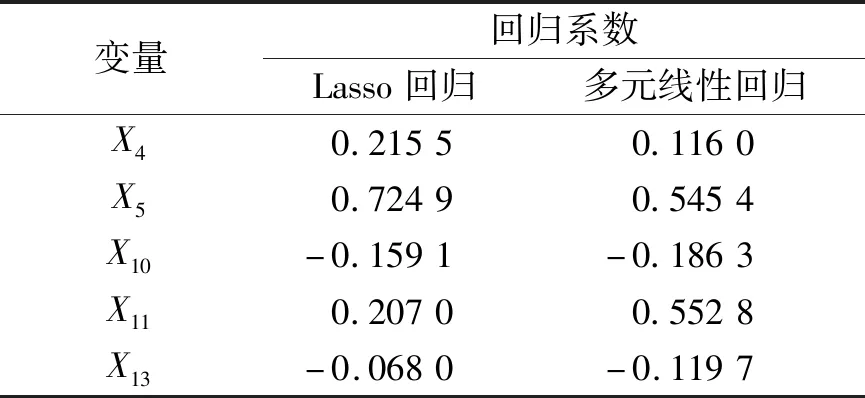
表3 Lasso回归分析变量筛选结果
2.2 灰色关联度分析
灰色关联度分析基本思想是根据序列曲线的几何形状的相似程度来判断其联系紧密程度,根据紧密度大小对关联度进行排序。令垃圾清运量为分析数列的母序列,影响垃圾清运量的各指标为子序列,则母序列与子序列的灰色关联系数ξXi和关联度γi为:
(2)
(3)
式中:Δ(min)为第二级最小差;Δ(max)为两级最大差;ΔXi(k)为各数列Xi曲线上的每一个点与参考数列X0曲线上的每一个点的绝对差值;k为子序列序号,ρ为分辨系数。
关联度γi值越接近1,说明相关性越好。选取关联度大于0.75的影响因素,如表4所示,可知灰色关联度分析筛选出的指标为:X4道理清扫保洁面积、X6城镇居民人均可支配收入、X7城镇居民人均消费支出、X8城镇人口数量、X12城市化率、X19教育程度。

表4 灰色关联度分析变量筛选结果
2.3 文献总结分析法
为使指标选取更全面,借鉴国内外垃圾预测相关文献,将其中选取的指标按4类罗列出,如表5所示。可知,建模时经常使用内在因素;学者普遍认为居民生活水平对垃圾产生影响是显著的;城市经济中,国内生产总值(GDP)是许多研究人员的首选,主要是因为更高的收入代表更高的潜在消费和产生更多的垃圾;人口也常常作为重要的影响垃圾量的指标,人口越多产生的生活垃圾也就越多;地域温度是一个广泛而有效的社会因素,但由于它的影响是难以计算的,因此很少将其纳入预测模型中。

表5 垃圾预测文献中所采用的指标及与垃圾量的相关系数
综合考虑内在因素各个方面及重庆市垃圾清运量与各指标间相关系数,笔者选用年末常住人口、GDP、第三产业增加值、道路清扫保洁面积、金融业增加值、城镇居民人均可支配收入和城镇居民人均消费性支出7个影响因素。
3 GA-BP神经网络的构建及拟合
通过不同方法进行影响因素筛选后,得出了不同的影响因素体系,但需判断哪个因素体系更能准确预测垃圾量,从而选取最佳的影响因素体系进行垃圾量预测。因此,构建GA-BP神经网络先对所选出的因素体系分别进行拟合,根据拟合程度选取影响因素体系,然后再进行垃圾量预测。
3.1 GA-BP神经网络的构建
BP神经网络具有学习、自组织、自适应和较强的容错性等特点,是一种按照误差逆向传播算法训练的多层前馈神经网络,是应用最广泛的神经网络。由于BP神经网络的每次训练都存在随机性,为了减少这种随机性及避免陷入局部极值,利用遗传算法(GA)全局寻优能力对神经网络的权值阈值进行优化,将优化后的权值、阈值作为神经网络的固定权值、阈值,具体流程如图1所示。神经网络模型由输入层、隐含层和输出层3层构成,各层的传输函数均为默认的函数,网络学习算法为LM算法,网络训练函数为trainlm函数。最大训练次数设为2 000,训练的收敛均方误差为0.001,隐含神经元个数为10。
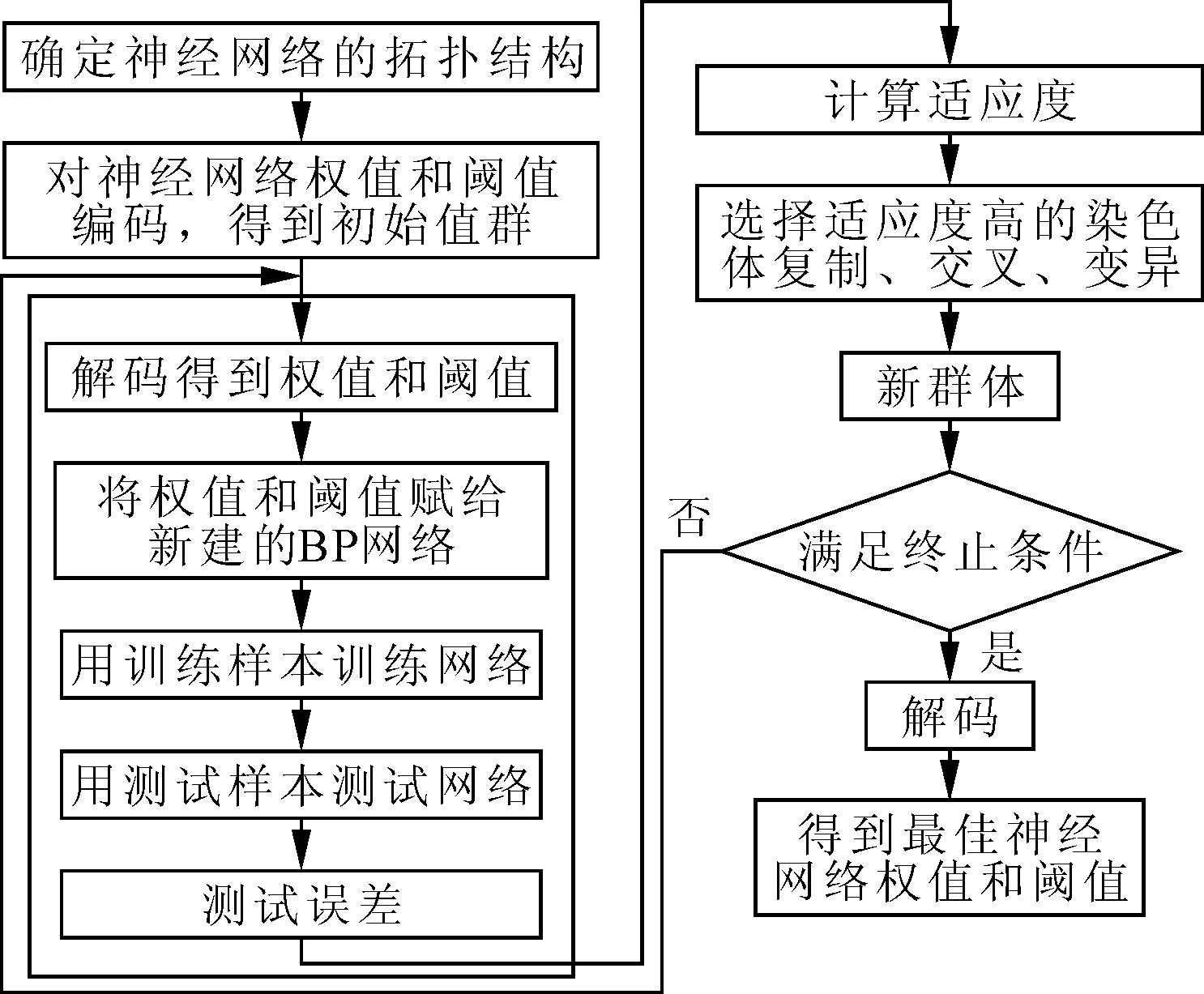
图1 GA优化BP神经网络阈值和权值
3.2 模型拟合结果分析
筛选出不同影响因素体系后,利用构建好的GA-BP网络对筛选的3种影响因素体系进行网络拟合,选出最佳的影响因素体系。选用2004—2016年的样本数据为训练集,2017—2018年的样本数据为测试集,随机运行10次,拟合结果如表6所示。
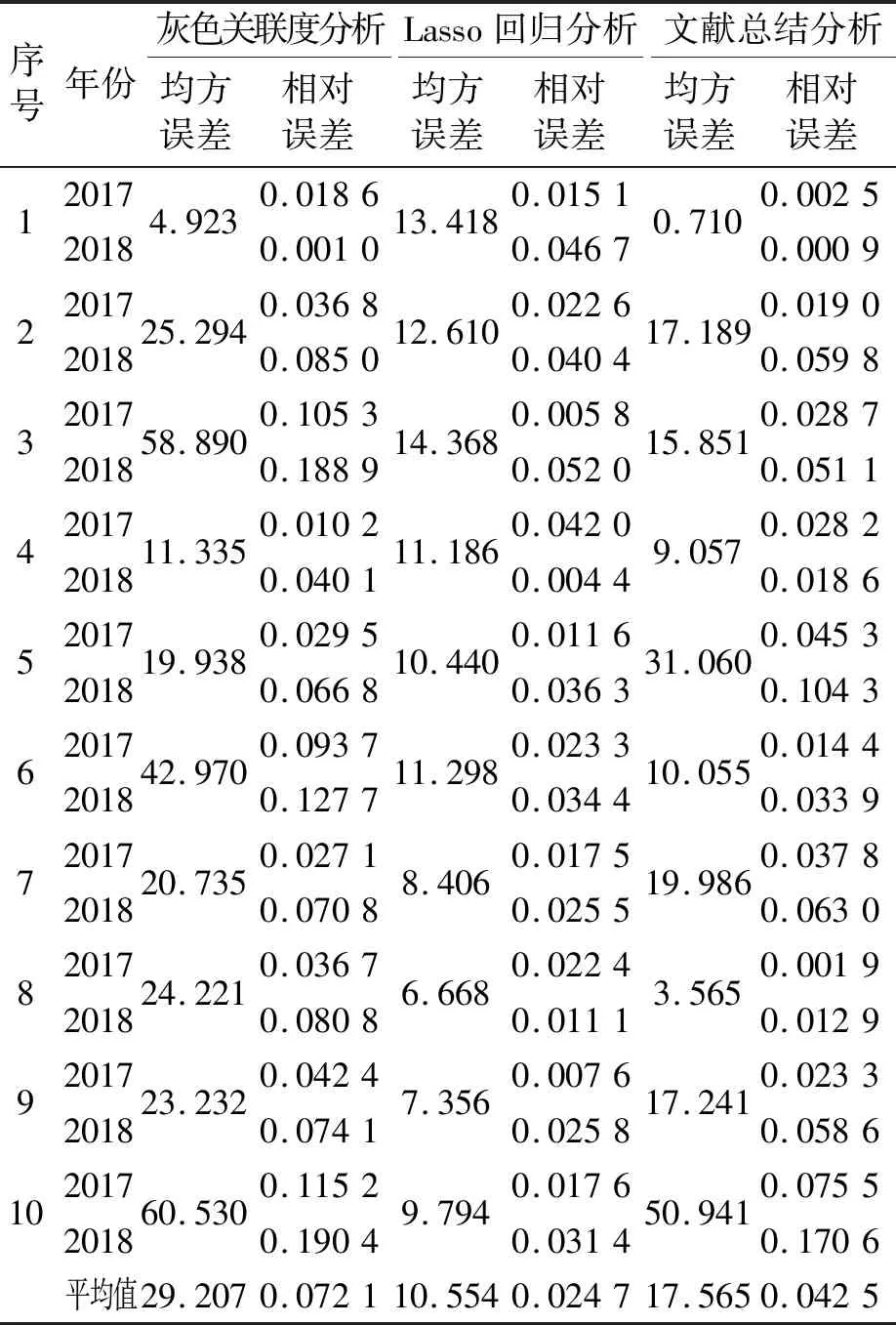
表6 各因素体系拟合误差结果
由表6可知,Lasso回归分析筛选出指标的拟合平均均方误差最小,为10.554,平均相对误差也最小,为0.024 7。故最终选用由Lasso回归分析筛选出的5个影响因素作为GA-BP神经网络模型的输入,影响因素及其回归系数如表7所示,再次进行拟合,网络在第80次运行后,其均方误差接近0。

表7 Lasso回归分析筛选出的影响因素与其回归系数
2017—2018年垃圾量拟合结果如表8所示,可知GA-BP模型拟合的平均相对误差为0.215%,即该模型的拟合程度高,且经GA优化后的网络性能优于单纯的BP网络模型。
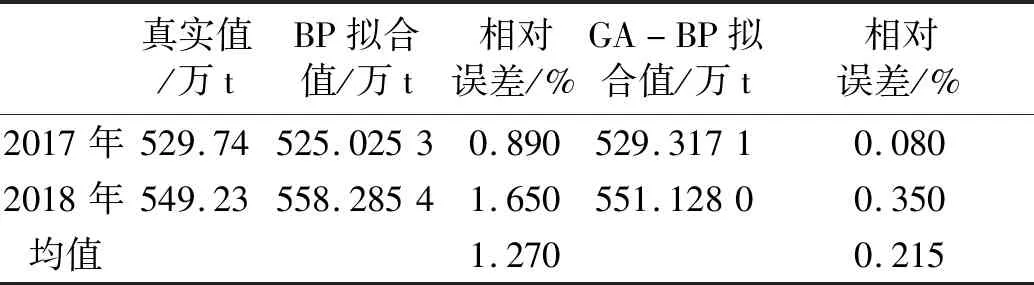
表8 2017—2018年垃圾量拟合结果
4 重庆市垃圾量预测
4.1 影响因素预测
对于影响因素的预测,选用能准确提取时间序列当前值、过去值及误差值之间回归关系的能力的ARIMA模型。ARIMA(p,d,q)模型是依据时间序列数据的过去值及现在值预测未来值的著名时间序列预测方法。ARIMA中的专家建模器会根据序列的特点选取统计显著关系的模型,必要时使用平方根、差分或自然对数转换对模型的变量做适当转换。ARIMA模型可表示为:
(4)
式中:p为自回归项数;q为滑动平均项数;d为使时间序列成为平稳序列时所做的差分次数;L为滞后算子。利用ARIMA模型对各个影响因素进行预测后,对各残差进行白噪声检验判断残差是否为白噪声,若残差是白噪声,则表示该时间序列的规律能被所选的模型完全识别。该时间序列能被模型完全识别,所有滞后阶数的自相关系数和偏自相关系数均与0没有显著的差异,即预测效果较好。各影响因素的预测结果如表9所示,其中对于X10城市气化率的预测2021年为100.07%,根据现实意义将其改为100%。
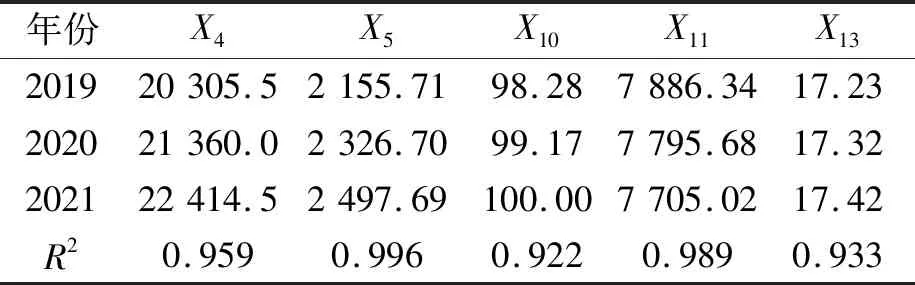
表9 影响因素预测值
4.2 垃圾量预测
将5个指标的预测值作为上述已训练好的GA-BP模型的输入,利用优化后的网络权值阈值进行最终的垃圾量预测,结果如表10所示,可知重庆市垃圾量在2021年将达到624.780万t。
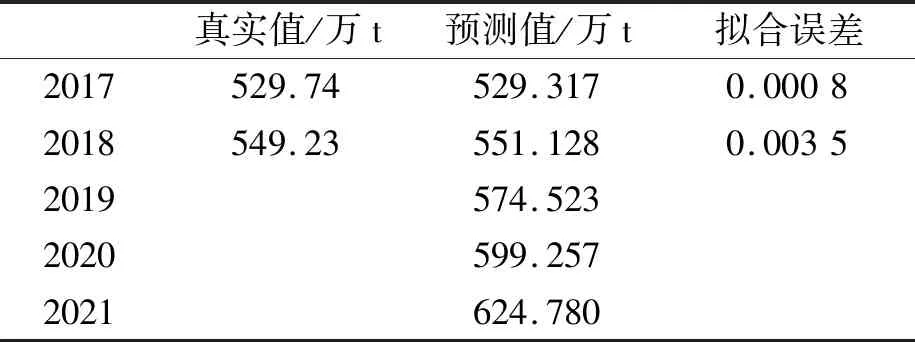
表10 重庆垃圾量预测结果
5 结论
(1)提出利用Lasso回归分析、灰色关联度分析、文献总结分析3种不同的方法对影响重庆垃圾量的因素进行筛选,对比拟合结果后,选取Lasso回归筛选出的影响因素体系,即道路清扫保洁面积、金融业增加值、城市气化率、社会零售额、人均绿地面积作为影响垃圾量的主要因素。
(2)采用时间序列预测方法ARIMA模型对未来3年的主要影响因素的数据进行预测,并对其进行白噪声残差检验。将GA-BP神经网络模型引入到垃圾量预测中,对重庆市未来3年的垃圾量进行预测,结果显示未来3年重庆市垃圾量的预测值分别为574.523万t、599.257万t、624.780万t。
(3)模型的拟合平均相对误差低至0.215%,比文献[2]对重庆市生活垃圾量预测的平均相对误差(4.576 5%)降低了4.361 5%。所提出的模型和方法,可为实际中的垃圾管理措施提供相应依据。
