高含硫气井井筒硫沉积模型

2022-06-13高子丘顾少华曾佳方博胡景宏

断块油气田 2022年1期

高子丘，顾少华，曾佳，方博，胡景宏

（1.中国地质大学（北京）非常规天然气地质评价与开发工程北京市重点实验室，北京 100083；2.中国石化石油勘探开发研究院中国石化海相油气田开发重点实验室，北京 100083；3.中国石油西南油气田分公司安全环保与技术监督研究院，四川成都 610041）

0 引言

随着常规油气藏开发逐渐衰竭，非常规油气藏逐渐成为当今油气资源开发的重要领域。高含硫气藏作为非常规气藏的一种，在我国四川盆地广泛分布，四川东北部，发现了诸如罗家寨气田、渡口河气田、普光气田、铁山坡气田[1-3]等一系列高含硫气田。但硫沉积一直是目前高含硫气藏开发面临的主要难题之一。这些气田开采时，在天然气流经的地层、井筒以及地面储运集输管道、容器中都会出现硫沉积现象。井筒中的硫沉积会在一定时间内形成硫垢，导致井筒堵塞[4-6]和产量急剧下降，甚至关井停产，而且因为天然气中的硫化氢具有剧毒性，使得实际生产过程中温度和压力的监测十分困难[7]；因此，建立合适的计算模型来预测井筒温度、压力的变化和井筒硫沉积非常重要。

井筒中的混合流体在上升过程中，会和周围的地层进行热交换。为此，之前 Ramey[8]和 Hasan 等[9]的模型将井筒与地层间的热传导考虑为稳态传热。前人的模型虽然能预测井筒温度，但所用计算方法却受到许多假设条件的限制（如假设流体在流动过程中不存在相变），且由于热传导实际上往往是非稳态的[10-14]，故这些模型难以解决复杂的实际问题。2015年，宋戈[15]提出的基于复合介质的井筒和地层的传热模型比较符合实际情况。对硫溶解度的计算，普遍采用Roberts[16]模型，然而此模型是根据特定组分的实验数据获得的，当硫化氢体积分数改变时并不适用。此外，其他模型[17-21]在计算精度上还有需要改进的地方。鉴于此，为更好地描述硫溶解度随压力和温度的变化关系，本文采用Hu等[22]建立的硫溶解度模型，该模型全面考虑了不同的天然气组分及天然气密度，计算精度较高。

井筒中气体的硫从析出到沉积是个动态过程[23-24]。在实际开发生产过程中，气体从井底到井口温度逐渐降低，硫溶解度随之下降，当硫溶解度降低到临界值的时候，混合于天然气中的硫开始析出。若气体流速小于硫颗粒临界悬浮流速，则硫颗粒不能被携带出井口，便会沉积下来附着在井壁[25]，形成硫垢；若硫垢越积越厚，则会导致井径缩小，同时影响传热，从而对整个井筒的温度、压力产生影响。硫单质（即析出的元素硫）从井底向井口运移的过程中，相态随着温度、压力的变化而变化，计算时，不同相态采用的温度、压力模型也不一样。当井筒内温度高于硫的熔点温度118.9℃时，井筒中析出的硫单质为液态，而温度低于118.9℃时，硫单质沉积（简称硫沉积）为固态。

针对硫沉积位置预测不准确的问题，本文基于热力学、传热学、流体力学等理论，首先建立了温度和压力相互耦合的预测模型[26-28]，然后结合硫溶解度计算模型，研究了硫溶解度沿着井筒的变化趋势，最后预测出硫沉积位置和沉积量。此外，本文还研究了气井日产量、硫化氢体积分数等相关因素对硫沉积的影响。硫沉积位置的预测，对指导现场生产具有重要意义。

1 井筒温度、压力计算模型

假设条件：1）气体在井筒内处于一维稳定流动状态；2）在井筒同一深度的横截面上，气体的物性参数处处相等；3）只考虑井筒和地层之间的径向传热，不考虑井筒垂向传热；4）系统总传热系数的计算忽略油管内壁及金属的热阻；5）将多相流体的管流状态近似地认为是单相管流，即拟单相管流，模型的对应参数为混合流体的相关参数。

1.1 温度计算模型

井筒径向介质、温度分布如图1（图中：rto，rh分别为油管外径和井眼（水泥环）外径，Tf为流体温度，Tti，Tto分别为油管内、外径处温度，Tci，Tco分别为套管内、外径处温度，Th为水泥环外径处温度）所示。本文将Ⅱ区（油管—水泥环外界的区域）和Ⅲ区（地层）的热传导都考虑为非稳态传热。在此基础上，通过非稳态传热的相关传热学理论计算出井筒至地层的散热量，然后结合相关模型进行井筒内的传热计算，以建立井筒温度模型。

图1 井筒径向介质、温度分布

1.1.1 井筒内热力学模型

根据能量守恒定律以及传热学相关理论，将比焓描述为温度和压力的函数，建立井筒内能量守恒方程：

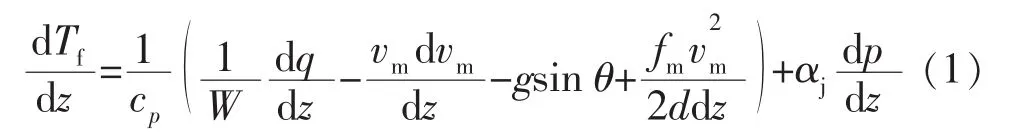
式中：cp为气体的质量定压热容，kJ/（kg·K）；q 为流体径向热流量，W；vm为混合流体速度，m3/s；z为井筒长度（井深），m；g为重力加速度，m/s2；W 为流体质量流量，kg/s；θ为管斜角（井筒与水平面之间的夹角），（°）；fm为混合流体摩阻系数；d为油管内径，m；αj为焦耳-汤姆逊系数，℃/MPa。

1.1.2 井筒—地层非稳态模型

1.2 压力计算模型

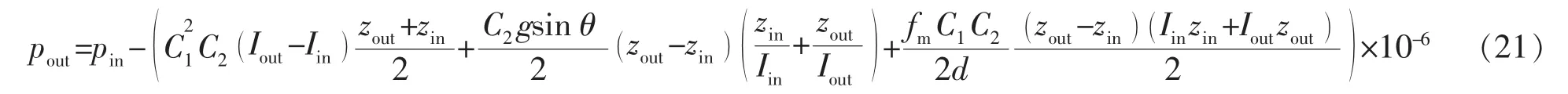
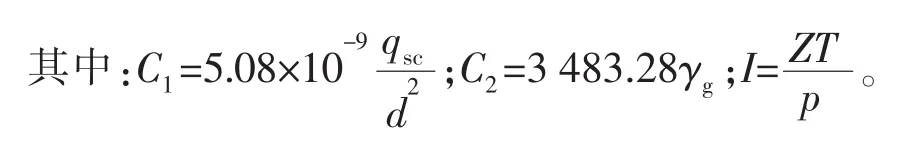
式中：pin，pout分别为单元控制体入口段和出口段的压力，MPa；zin，zout分别为单元控制体入口段和出口段的纵向距离，m；qsc为气井产气量，m3/d；γg为天然气相对密度；Z为偏差因子；T为温度，K；p为压力，MPa。

根据式（21），即可得整个井筒的压力分布。

当vm>vmcr时，硫单质被混合流体携带至井口；当vm≤vmcr时，硫单质悬浮在井筒中或向下沉降。

若硫单质可以沉积在井筒内，则沉积量为

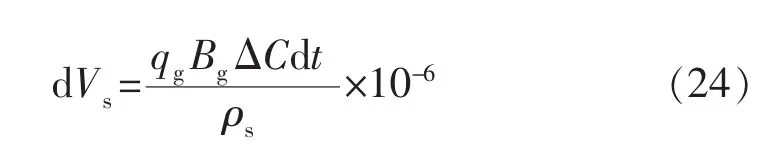
式中：Vs为析出的硫体积，m3；Bg为天然气体积系数；qg为气井产量，m3/d；t为生产时间，d。

2 硫沉积预测模型

2.1 硫溶解度预测模型

采用 Hu 等[22]的硫溶解度模型（式（22））预测井筒的硫溶解度，具体参数见表1。

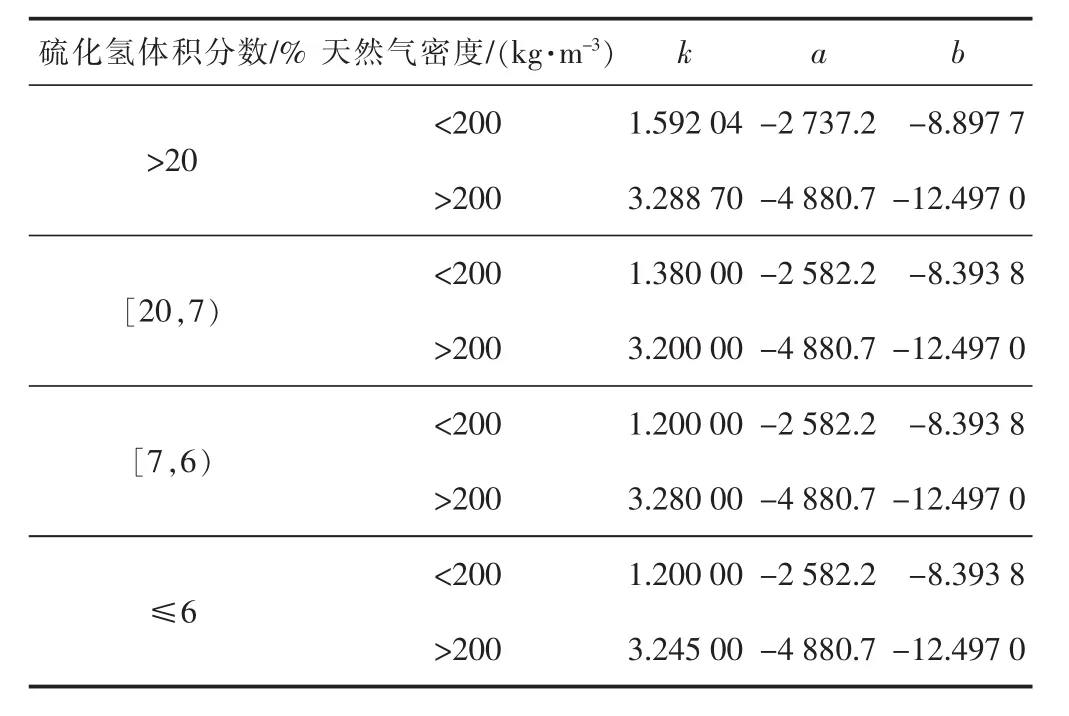
表1 模型参数取值

式中：Cs为硫溶解度，g/m3；ρ为流体密度，kg/m3；k，a，b均为经验常数。

2.2 临界悬浮流速与沉积量模型

硫单质是否会沉积在井筒内取决于其流速与临界悬浮流速的关系。混合流体携带硫单质所需的临界悬浮流速为

式中：vmcr为混合流体携带硫单质所需的临界悬浮流速，m/s；Vs为硫单质体积，m3；ρs为硫单质密度， kg/m3（一般为2 070 kg/m3）；Cd为雷诺数相关的函数；S为硫单质的横截面积，m2。

首先，利用式（17）、（21）计算井筒内温度、压力分布，根据硫化氢体积分数从表1中选取对应参数，进而求得硫溶解度——若其大于临界硫溶解度，则可确定硫析出位置。其次，根据式（23）判断硫单质是否沉积在井筒内。根据其相态再次重新计算，最终可得出整个井筒的温度、压力、硫溶解度的计算模型。联立式（17）、（21）、（22），得：

3 实例分析

以位于加拿大Devonian Wabamun地层的某口高含硫气井X井为例[29]。基础数据见表2、表3。井底初始含硫量为137.38 g/m3，生产过程中首次发现有硫沉积的位置在井深3 468.2 m处。利用表中数据验证硫沉积预测模型的准确性。

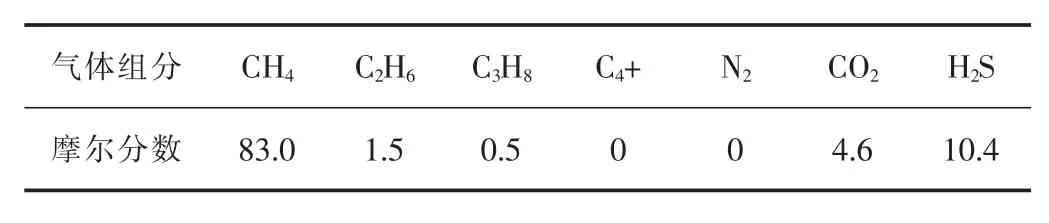
表2 气体组分 %

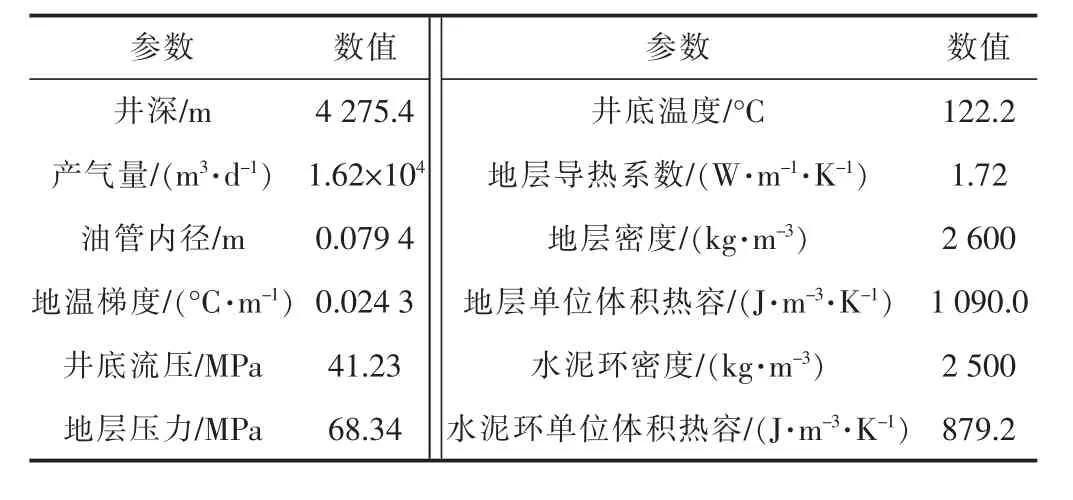
表3 X井基本参数

产气量对硫溶解度的影响见图2。

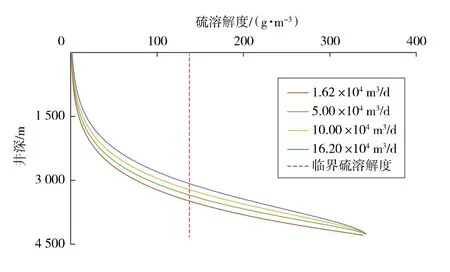
图2 产气量对硫溶解度的影响

由图2可知，硫溶解度从井底到井口逐渐减小，这是因为温度、压力逐渐降低。当产气量分别为1.62×104，5.00×104，10.00×104，16.20×104m3/d 时，硫溶解度逐渐增大。因为产气量增大，井筒内的温度升高，由式（22）可知，溶解度变小，硫临界溶解度对应的位置提高，分别为 3 480，3 390，3 270，3 210 m。可以看出，当产气量为1.62×104m3/d时，初始硫析出（沉积）位置在3 480 m，与实例的3 468.2 m相比，误差小于1%，说明本文建立的模型具有较好的准确性。在井深3 480 m处，井筒的温度为107.85℃，低于硫的熔点温度118.9℃，所以，析出的单质硫为固体硫颗粒，并沉积。

生产时间及产气量对井筒温度的影响见图3。

图3 生产时间及产气量对井筒温度的影响

由图3a可以看出，随着生产时间的增加，井筒径向传热使得井筒附近地层温度上升，井筒与附近地层温度差和传热量减小，因此井筒内温度不断升高。而由图3b可知，产气量增大，使得气体流速增加，气体流动时携带出井口的热量越多，沿程损失的热量越少，因此产气量越大，井口温度越高。

生产时间及产气量对压力的影响如图4所示。

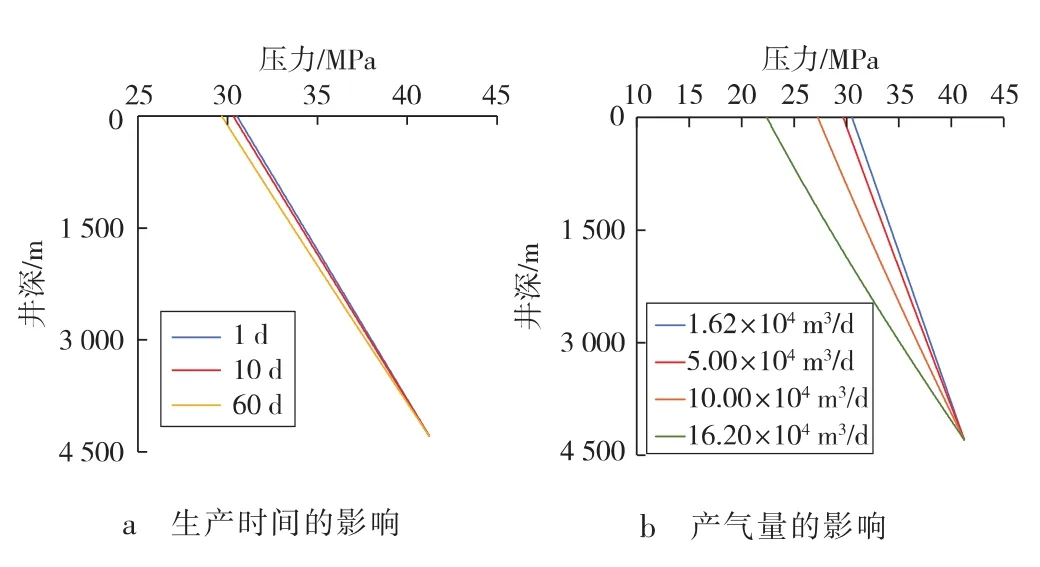
图4 生产时间及产气量对井筒压力的影响

由图4可知：随着生产时间的增加，同一深度的压力逐渐减小。这是地层的能量随着生产的进行逐渐减小造成的。随着产气量的增加，井口压力降低，且变化幅度不大。这是因为产气量越大，气体流速越快，井筒中的压力下降梯度越大。在井底压力不变的情况下，产气量的增加会导致整个井筒压力降低。此外，还可看出温度沿井筒呈现非线性分布，而压力则是线性分布。

由图5a可以看出，以产气量1.62×104m3/d、生产时间4 d计算，当硫化氢体积分数分别为5.2%，10.4%，20.8%时，硫沉积位置分别在3 420，3 480，3 540 m。原因在于硫化氢的体积分数改变了气体组分的占比，混合流体的密度也因此发生改变，从而影响温度、压力和硫溶解度。当硫化氢体积分数增大时，硫更容易析出，硫的析出位置下降，硫析出体积略微减小。由图5b可知：当产气量为 1.62×104，5.00×104m3/d 时，井筒内相同位置处硫析出量增大，因为井筒单位体积内流过的气体更多；析出位置分别在3 480，3 390 m，略微上升，这是因为产气量增加，使得温度上升。此外，本文还计算了产气量为10.00×104m3/d的情况，此时气体的流速大于临界悬浮流速，无硫沉积。