页岩油致密储层一体化压裂裂缝穿层扩展特征
2022-06-13崔壮侯冰付世豪吕嘉昕
崔壮,侯冰,付世豪,吕嘉昕
(1.中国石油大学(北京)油气资源与探测国家重点实验室,北京 102249;2.中国石油大学(北京)石油工程教育部重点实验室,北京 102249)
准噶尔盆地吉木萨尔凹陷芦草沟组发育的致密砂泥岩薄互层中,砂岩、泥岩交替叠置,纵向储隔层交互发育、“甜点”分散、单层开发成本高[1-5]。 采用一体化穿层压裂技术开采页岩油对非常规油气的规模开发和降本增效具有重要意义,为实现不同层系差异组合开发,必须促使水力裂缝在纵向上有效连通不同层系。但是致密砂泥岩薄互层非均质特征明显,孔隙度、渗透率、弹性模量等物理性质和力学参数差异显著,水力裂缝纵向扩展受到严重抑制,压裂改造难以形成高效导流的支撑缝;同时层间应力差异明显,弱结构面发育,泥岩夹层呈薄互层状,使得岩石的破坏方式和水力裂缝扩展形态变得十分复杂,压裂改造措施难以实施[6-8]。因此,如何提高砂泥岩薄互层缝网复杂程度和缝高扩展能力,是一体化穿层压裂技术的关键所在。
国内外学者针对水力裂缝在多岩性组合层状储层中的纵向延伸规律进行了大量研究。这些研究基于物理模拟实验,建立了页岩油储层的水力裂缝缝高控制方法,创建了水力裂缝扩展模型[9-15],发现水力裂缝在层状页岩储层垂直面呈现出多种扩展模式,主要是钝化缝、“工”形缝、类鱼骨缝等,同时发现天然层理面、层间应力差、储层厚度等是影响裂缝穿层扩展的内在因素[16-19]。 Damjanac 等[20]采用离散元的方法研究了泥页岩储层中岩石力学性质差异对裂缝缝高扩展的影响。Zhao 等[21-22]基于损伤力学的内聚区法建立了致密页岩层系裂缝扩展模型,研究了施工参数和地质条件对裂缝垂向扩展的影响,初步掌握了砂岩和页岩交互层裂缝垂向扩展规律。Xie等[23]基于三维位移不连续法研究层理面对裂缝垂向扩展的影响,发现沿层理面的剪切位移是裂缝垂向扩展的主要机制。Heng等[24]通过物理模拟实验和数值模型验证,揭示了页岩层系水力裂缝在层理面渗透、受阻或偏转的机制。Dong等[25]基于有限差分法建立了泥页岩层系裂缝扩展模型,研究了水平主应力差、界面摩擦因数和岩石抗拉强度对裂缝垂向扩展的影响。然而,这些研究主要集中在单一岩性的缝高控制上,并未考虑缝长和缝高同时竞争扩展过程,或是缺乏对岩性界面强度的考虑,同时较少涉及多岩性叠置的页岩油储层一体化穿层压裂技术。
本文基于准噶尔盆地吉木萨尔凹陷芦草沟组砂泥岩薄互层地质特征,建立三维水力裂缝穿层扩展模型,开展砂泥岩薄互层水力裂缝扩展的数值模拟研究,探究三维空间下缝长与缝高共同扩展时的裂缝穿层行为,定量表征薄互层岩性界面强度和层间应力等参数对裂缝穿层扩展造缝的综合影响,准确预测砂泥岩薄互层水力裂缝穿层扩展形态,以期为砂泥岩储层实际地质工程一体化穿层压裂提供指导。
1 砂泥岩储层地质特征
准噶尔盆地东部隆起吉木萨尔凹陷自下而上划分为芦草沟组一段和二段2套致密型砂泥岩正旋回储盖组合,纵向上存在2个“甜点”集中发育段。其中:下“甜点”体位于芦一段二层组中上部,厚度17.5~67.5 m,平均41.5 m;上“甜点”体位于芦二段二层组中上部,厚度13.4~43.0 m,平均37.8 m。芦草沟组地层岩性矿物成分复杂,纵向岩性交替改变,泥岩夹层薄,呈砂泥岩薄互层状,层理面发育,层间非均质性强且天然裂缝特征差异显著。图1为芦草沟组地层特征,储层纵向剖面岩性复杂,岩石力学特征及应力条件差异大,最大层间应力差可达到5 MPa。砂泥岩薄互层较多的天然弱结构面会消耗压裂液能量,使裂缝出现延伸卡点,缝高扩展受到限制,相比传统单层砂岩储层,砂泥岩薄互层复杂的地层环境及应力状态,使得水力裂缝一体化穿层扩展十分困难。

图1 芦草沟组砂泥岩薄互层地质特征
2 数学模型
水力裂缝扩展数值模型多为简化的二维模型,忽略了缝长和缝高的竞争扩展过程,或者岩性界面强度的影响,导致计算的缝高远大于实际缝高。黏聚单元法采用牵引-分离定律定义裂纹扩展区域,水力裂缝尖端应力奇异的问题被优化[26-27]。 因此,本文选择 Cohesive单元法描述砂泥岩互层缝高发育特征,探究三维空间缝长与缝高共同扩展时的裂缝穿层行为。
2.1 控制方程
2.1.1 流-固耦合方程
岩石属于一种多孔介质,可使用有效应力原理表征应力渗流耦合关系:
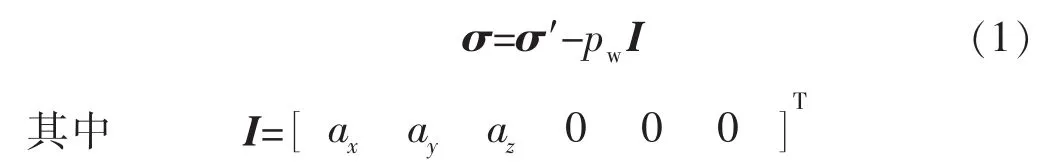
式中:σ为总应力矩阵;σ′为有效应力矩阵;pw为孔隙压力;ax,ay,az分别为 x,y,z方向的 Biot系数。
黏性单元体积为V,表面积为S,岩石固体骨架变形力学的平衡方程[28]为
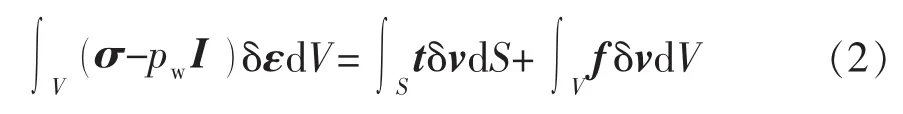
式中:ε为虚应变率矩阵;v为虚速度矩阵;t为表面力矩阵;f为体力矩阵。
流体渗流的质量守恒方程[29]为

式中:J为体积变化率;ρw为流体密度;nw为孔隙度;vw为流体渗流速度。
流体在岩石内流动的动量方程满足达西定律:
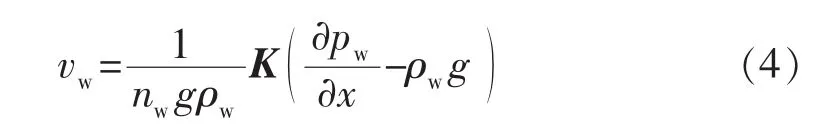
式中:g为重力加速度;K为岩石渗透率张量。
2.1.2 水力裂缝起裂与扩展准则
本文采用最大主应力准则判断黏性单元是否发生初始损伤,即假定3个方向中某个方向的应力值与对应临界值的比值大于1时,水力裂缝起裂开始[30],即

式中:σn为法向应力;τs,τt分别为 2 个方向的切向应力;〈〉表示黏性单元受拉应力、压应力时不产生损伤;上标max表示临界。
一个损伤模型通常包括起裂准则、损伤演化法则和失效后处理3个部分。裂缝扩展过程采用Cohesive单元刚度衰减进行描述,3个方向的应力表达式[31]为

式中:tn为实际法向应力;D为损伤因子;为未损伤法向应力,表征黏性单元整体破坏程度;ts,tt分别为2个方向的切向应力;分别为2个方向的未损伤切向应力。
黏聚力受界面损伤因子控制,图2为基于线性位移准则的损伤演化过程(横坐标δ为黏性单元张开位移,纵坐标T为应力,T0为初始损伤应力;绿色箭头表示黏性单元起裂后的刚度变化)。在单元损伤开始后,D从0到1呈线性增加,其表达式为

图2 牵引-分离准则

式中:δ0,δf分别为初始、完成损伤位移;δm为最大位移。
2.1.3 缝内流体流动方程
本研究的压裂液为不可压缩的牛顿流体在水力裂缝内切向流动,即:

式中:q为切向流量;w为裂缝宽度;μ为压裂液黏度;∇p为流体压力梯度。
考虑压裂液沿水力裂缝向岩石的上、下表面滤失,则流动方程[32]为

式中:qt,qb分别为上、下表面流量;ct,cb分别为上、下表面滤失系数;pi为水力裂缝内流体压力;pt,pb分别为上、下表面孔隙压力。
缝内流体的流动满足连续性方程,即:

式中:Q(t)为压裂液注入量;t为时间。
联立式(8)—(10),可得雷诺润湿方程:

2.1.4 界面摩擦准则
岩性界面抗剪强度大于剪切应力时,界面出现滑动摩擦。本文采用库伦摩擦定律计算剪切应力,即:

2.2 模型建立及验证
图3是本文建立的三维流-固耦合数值模型(σv为垂向主应力,σH为最大水平主应力,σh为最小水平主应力)。为了研究层间应力差异对裂缝穿层扩展的影响和水力裂缝与岩性界面的作用机理,定量表征薄互层界面强度、层间应力差和层内应力差综合影响下的裂缝穿层扩展行为,将三维流-固耦合水力裂缝扩展模型根据地层实际情况简化为5层实体,其中,顶层、中间层和底层的计算参数一致。在x和y方向上预置Cohesive单元面,分别用于模拟岩性界面和水力裂缝扩展路径。模型每层厚度为10 m,压裂液注入点位于中间层,三维模型尺寸为100 m×50 m×50 m,实体单元C3D8P表征储层岩石在三维空间内的变形破坏和孔隙流体渗流。
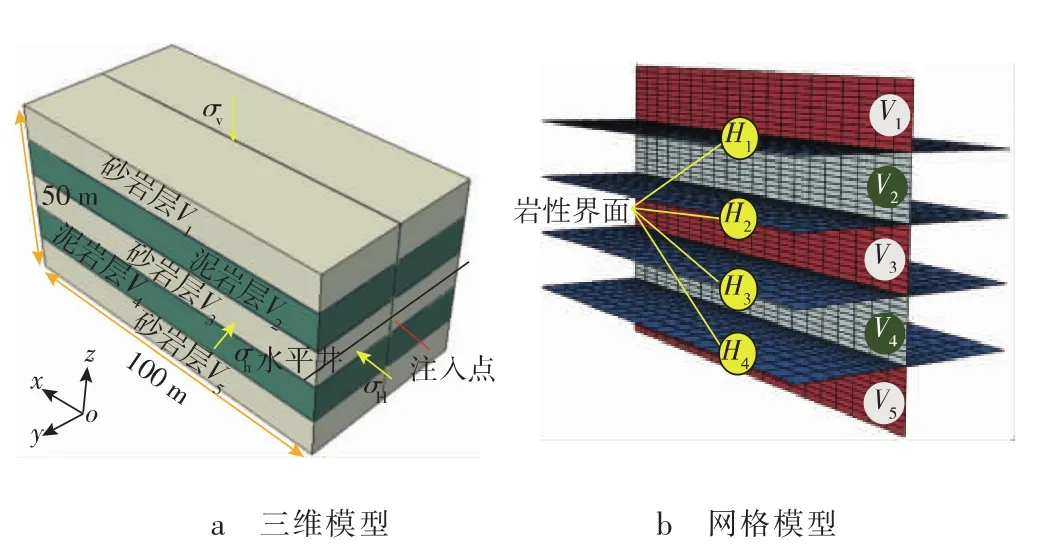
图3 三维流-固耦合数值模型
为了提高计算的精度和收敛性,模型使用高级算法和局部加密网格,对水力裂缝扩展路径周围的网格进行加密处理。在综合考虑芦草沟组砂泥岩薄互层特征的基础上,设置模型输入参数,如表1、表2所示。
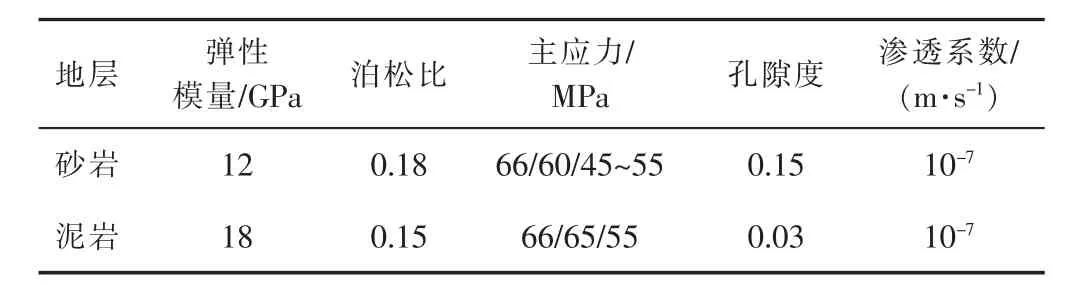
表1 岩石基质模型参数

表2 预置Cohesive单元面模型参数
为了验证该数值方法的可行性,采用基准模型,与Savitski等[33]推导的解析解进行对比。Savitski推导的裂缝宽度和水力裂缝径向距离表达式分别为
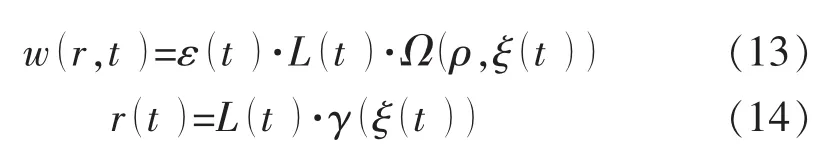
式中:r为径向距离;ε(t)为无因次小量;L(t)为裂缝长度;Ω为裂缝实时缝宽;ξ(t)为时间函数;ρ为无因次坐标,在裂缝平面构建,取值范围为0~1;γ为缝长。
图4给出了裂缝宽度沿径向变化的数值解与解析解,除裂缝尖端缝宽有微小差异,结果基本一致,验证了Cohesive方法模拟水力裂缝穿层扩展的准确性。

图4 裂缝宽度与径向距离数值解与解析解对比
3 模拟结果及分析
3.1 水力裂缝形态
数值模拟结果如图5所示,图中左侧是前视图,右侧是45°侧视图。由于应力及岩性界面强度差异,水力裂缝破坏岩性界面方式不断改变,最终表现出4类典型裂缝扩展形态:1)钝化缝,即水力裂缝呈波纹状扩展模式,但是垂向上接触岩性界面后立即停止扩展;2)T形缝,即裂缝垂向扩展至岩性界面后,缝尖钝化,缝高停止扩展,缝长和缝宽逐渐增大,转为经典的PKN扩展模式,主水力裂缝表现为拉伸破坏,而岩性界面初始为剪切破坏,逐步随裂缝转为张性破坏;3)鱼骨缝,即主水力裂缝垂直延伸,扩展至岩性界面时,由于岩性界面胶结强度低,使得岩性界面同步发生剪切破坏;4)穿层缝,即水力裂缝垂向扩展至岩性界面,裂缝前端缝尖钝化,沿垂直方向起裂沟通多个层系。

图5 不同类型水力裂缝扩展示意
3.2 水力裂缝形态影响因素
3.2.1 层内应力差
应力对水力裂缝的几何形态有显著影响。当砂泥岩互层无层间应力差时,垂向应力差异系数是能否形成复杂裂缝系统的主要因素[34]。砂泥岩互层应力条件差异巨大,因此本文设置垂向应力差异系数的数值为0~1,模拟在垂向应力差条件下的水力裂缝扩展形态:

式中:ζv为垂向应力差异系数;σR,h为中间砂岩层最小水平主应力。
图6为砂泥岩薄互层岩性界面破坏方式和裂缝扩展形态。垂向应力差对水力裂缝能否形成复杂裂缝网络有重要影响。0<ζv<0.2时,主裂缝延伸至岩性界面,形成钝化缝或T形缝,无法沟通相邻储层;0.2≤ζv≤0.5时,主裂缝与岩性界面相互作用,穿透岩性界面形成复杂鱼骨缝,岩性界面从剪切破坏转为拉伸破坏;ζv>0.5时,主裂缝穿透岩性界面,但是不发生转向延伸,主要形成单一穿层缝。分析认为,界面摩擦因数不变时,临界破坏时对应的摩擦剪应力随垂向应力差异系数减小而减小,较小的摩擦剪应力会使裂缝沿岩性界面扩展,缝穿透岩性界面进入相邻层位扩展,容易沟通相邻储层,形成复杂裂缝网络,获得较大的储层改造体积。

图6 水力裂缝起裂与扩展特征
3.2.2 层间应力差
砂泥岩薄互层纵向岩石力学特性及应力条件差异大,最大层间应力差可达10 MPa,因此需要考虑垂向和水平应力差异系数的综合影响。本文设置水平最小主应力差异系数的数值为0~0.25,模拟实际储层在层间和层内应力条件下的水力裂缝扩展形态。

式中:ζh为水平最小主应力差异系数;σB,h为泥岩层最小水平主应力。
结果表明,水平最小主应力差异系数对水力裂缝能否穿层扩展有重要影响。0<ζh<0.12时,主裂缝穿透岩性界面,形成穿层缝或鱼骨缝;ζh≥0.12时,主裂缝在岩性界面上产生横向滑移,缝高扩展受限,难以沟通相邻产层,主要形成T形缝或钝化缝。分析认为,当正应力及界面摩擦因数不变时,临界摩擦剪应力限制缝高扩展,层间水平最小主应力差异系数控制主裂缝垂向穿层扩展。因此层间应力差越小,裂缝越容易沟通相邻储层形成复杂裂缝网络。侯冰等[35]通过大量的真三轴物理模拟实验发现,层间应力差较大地限制了水力裂缝的转向行为,难以形成复杂裂缝网络,因此数值模拟结果与物理模拟结果吻合。根据不同层间水平最小主应力差异系数和层间垂向应力差异系数下的数值模拟结果,绘制如图7所示的综合影响图版。

图7 水平最小主应力差异系数和垂向应力差异系数的综合影响
3.2.3 无因次岩性界面强度
为定量表征岩性界面强度,根据储层和界面层内聚力单元强度的关系,定义无因次岩性界面强度[36]:
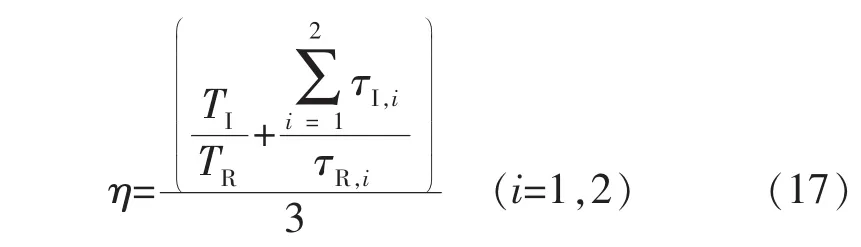
式中:η为无因次岩性界面强度;TI为界面抗拉强度;TR为储层抗拉强度;τI,i为界面第 i切向的内聚力;τR,i为储层第i切向的内聚力。
结果表明:当η小于0.10时,仅能形成钝化缝,裂缝无法穿层扩展;当η在0.15~0.25时,垂向应力差异系数决定是否形成T形缝或鱼骨缝,水平最小主应力差异系数与其无关(见图8);η增加到0.30时,水力裂缝沿岩性界面转向减少,缝高延伸远,损伤单元增加,有利于穿层扩展。分析认为,随着界面内聚力单元强度增加,水力裂缝渐进到岩性界面时,达到初始损伤条件的内聚力单元减少,裂缝不易转向,有利于水力裂缝穿层扩展。

图8 岩性界面强度和垂向应力差异系数的综合影响
4 现场应用
准噶尔盆地吉木萨尔凹陷页岩油藏压裂改造中,W3H井水平段长度为1 500 m,施工井段地层深度为3 050~3 200 m,注入总液量为42 399.5 m3,加砂量为2 686.65 m3,最大施工排量为14.45 m3/min。通过微地震信号反演出W3H井压裂缝网扩展空间形态[37](见图9)。左侧区域井段水平最小主应力差异系数为0.10,储层物性较好,水力裂缝垂向扩展,多数裂缝形态呈现穿层缝或者鱼骨缝;右侧区域井段水平最小主应力差异系数达0.18,裂缝形态大多呈现钝化缝或者T形缝;平面上以网状分布为主,储层穿层压裂改造效果较差。吉木萨尔凹陷砂泥岩薄互层应力条件复杂,天然裂缝发育程度不均匀,储层非均质性强,因此现场微地震数据反演出来的裂缝形态复杂多样,但是多数缝网形态为这4种典型裂缝的组合。研究结果可为优选页岩油层系一体化穿层压裂层位与实现多岩性叠置页岩油层系增产改造目标提供指导。
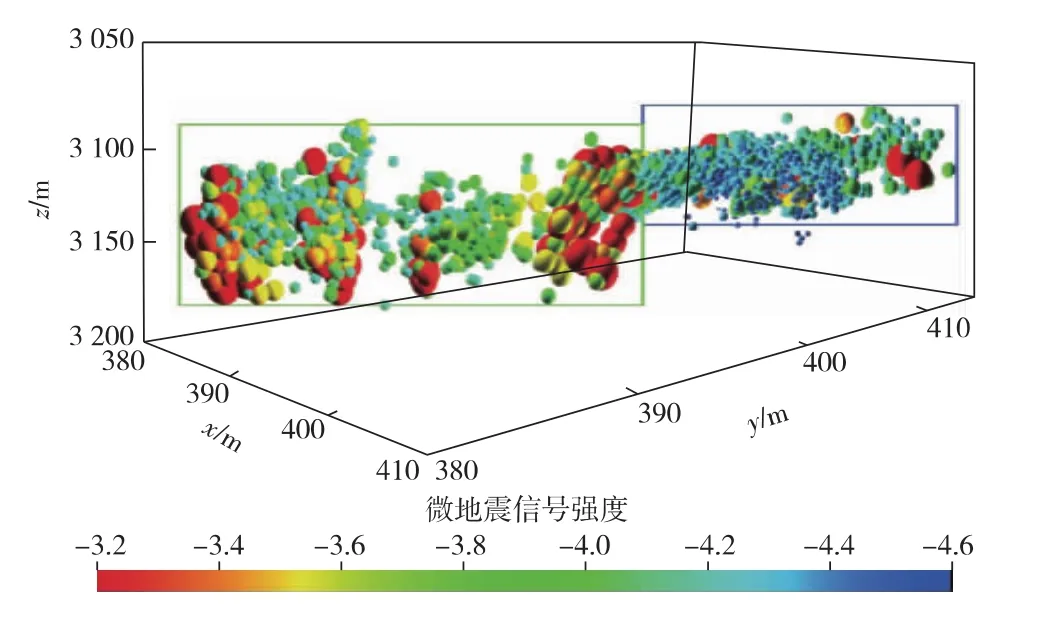
图9 吉木萨尔凹陷W3H井微地震监测结果空间展布
5 结论
1)根据水力裂缝与岩性界面接触方式的不同,可总结出4类典型裂缝形态——T形缝、钝化缝、鱼骨缝和穿层缝。主水力裂缝的破裂形式均为拉伸破坏,岩性界面的初始破裂形式均为剪切破坏。
2)垂向应力差异系数在0.2~0.5时,水力裂缝易于沟通岩性界面,形成复杂裂缝缝网;层间水平最小主应力差异系数越小,裂缝越容易穿透岩性界面扩展进入相邻层位。
3)随着无因次岩性界面强度增加,水力裂缝沿岩性界面转向减少。无因次岩性界面强度在0.15~0.25时,是否会形成鱼骨缝或穿层缝,由垂向应力差异系数决定,与水平最小主应力差异系数无关。
4)吉木萨尔凹陷页岩油藏压裂改造中,有利于产生网状裂缝和获得较大储层改造体积的条件为:垂向应力差异系数0.2~0.5,层间水平最小主应力差异系数小于0.12,无因次岩性界面强度0.15~0.25。
