顾及GNSS水汽分布特性和站间距离的优化IDW插值方法
2022-06-11闫香蓉王晓春梁薇穆雅璇宋雨龙丁楠张文渊
闫香蓉 王晓春 梁薇 穆雅璇 宋雨龙 丁楠 张文渊
0 引言
水汽在大气中含量很少,仅占大气总量的0~4%,同时水汽分布极不均匀,在短时间内变化速率快,常规一日两次探空气球获取的稀疏气象数据难以满足实时监测需求.台风、暴雨等极端天气都与水汽时空变化密切相关,准确快速地获取高时空分辨率的水汽观测资料对天气、气候变化研究和天气预报业务具有重要意义[1].
目前,常见的大气水汽探测方法有:无线电探测仪、气象卫星观测、水汽辐射计、红外雷达探测、太阳光谱分析仪等[2].相较传统的大气水汽监测方法,通过遥感(Remote Sensing,RS)红外数据和全球导航卫星系统(Global Navigation Satellite System,GNSS)数据都可以获取大气可降水量(Precipitable Water Vapor,PWV).遥感红外数据具有大范围、高时空分辨率的优势,通过不同时空亮温和辐射传输比直接反演大气水汽含量,一般应用分裂窗方法来反演,但是,遥感数据对低层的水汽难以测量[3].GNSS水汽探测具有连续运行、高精度、高时空分辨率等优点,利用GNSS技术进行大气水汽反演往往需要获得相应的地面气压和地面温度等气象数据,但由于大部分GNSS观测站建设时没有安装气象传感器,致使这些数据无法应用于气象变化研究[4],且水汽信息受观测站网密度影响较大.因此,合适的插值方法可以有效改善GNSS数据空间分辨率受站网密度影响的问题.
诸多学者围绕大气可降水量的季节性、区域性、变化特征与实际降水量的关系以及在暴雨预报中的应用等方面对各类插值方法进行了具体的研究[5-9].李颖等[10]应用交叉验证法对反距离加权法、全局多项式法、局部多项式法、径向基函数法、普通克里金法5种常用空间插值方法对PWV数据进行插值,对比分析各方法的精度,得出了随着大气可降水量平均值的提高,插值的误差趋于增大而相对误差趋于减小的结论.其中空间反距离权重法(Inverse Distance Weighting,IDW)的权重幂数和搜索半径会影响插值精度,对相关参数的估计过分依赖于经验,缺乏理论支持;对未知点数据估计的好坏依赖于样本点的布局[11],当采样点分布不均匀时,IDW方法会带来较大的插值误差.
针对上述问题,本文提出了一种顾及GNSS水汽分布特性和站间距离的优化IDW插值方法,该方法通过分析GNSS大气水汽特性与站点间距离对插值结果的影响,来确定最优化的插值参数,进而获得高质量的大气水汽插值结果.实验利用徐州地区的大气水汽数据进行实例验证,结果表明新方法反演高分辨率大气水汽可适用于GNSS站网布设较为稀疏的地区,有效提高了大气水汽重构精度.
1 常用的插值方法原理
本文使用3种性能良好的传统插值方法进行交叉验证,对比分析各方法的插值质量,并对IDW方法优化,提高计算得到的PWV数据质量及稳定性.
1.1 线性插值三角网法
线性插值三角网法(Triangulation with Linear Interpolation),是指将二维空间中具备参数值的多个空间点通过直线连接,构建若干插值三角形进行计算,建立起来的所有三角形面积覆盖整个研究区域,其中任一三角形的边不能与其他三角形相交,组成由若干个三角形拼接形成的研究网.线性插值三角网法能够很好体现原始数据的特征,它将整个研究区域内的数据进行均匀分配,分配完成后可在数据分布较少的区域得到一个拥有独特性质的三角面,以此计算得到一个最优插值结果.其计算公式为

(1)
式中:已知测站点的坐标为(x0,y0)和(x1,y1),yi为测区内一点(xi,yi)处的线性插值计算结果.虽然使用线性插值三角网法能较快计算得到插值结果,但其具有一定程度的局限性[12],受大气可降水量平均值影响较大,同时使用该方法计算的数据量少时难以保证其插值计算结果的平滑性[13].
1.2 克里金插值法
克里金插值法,即Kriging插值法,也称空间自协方差最佳插值方法.Kriging方法考虑观测点与估计点之间的相对位置信息,利用观测点之间的空间位置信息对待求点进行无偏和最优估计[14].克里金插值法的公式为

(2)
式中:ki为待定(克里金)权重系数,其值之和等于1,插值计算中观测站的个数为n,观测站的位置为xi,Z(xi)为在xi处的观测值.
1.3 空间反距离加权法
空间反距离权重法,也称为反距离加权法.该方法主要依赖于反距离的幂值,它的幂参数可以根据已知点和待插值点的距离来控制已知点对插值点的精度影响.该方法用周边采样点的值,估计未知点的值,以待插点与实际观测样本点之间的距离为权重,离插值点越近的样本点赋予的权重越大,其权重贡献与距离成反比.反距离加权法[15]的公式为
(3)
式中S处的预测值为Z(S0),计算过程使用的样本数量为n,di为插值点与已知点间的距离,Zi为对应样本点的值,p为幂参数,一般情况下,p取2.
2 顾及GNSS水汽特性和站间距离的优化IDW插值方法
2.1 GNSS数据介绍
本文以徐州市2017年的GNSS数据为基础,考虑到徐州地区夏季多雨冬季少雨的降水空间分布特性,选取5—7月降水相对集中且充足的时段开展实验,选取6个站点作为研究对象,测站名分别为:CHG0、DSH0、HJG0、SHG0、TSG0、TUG0,IGS辅助站分别为:YAKT、GUAM、POL2,探空气象数据为2017-05-11—2017-07-31有完整数据的共75 d的数据.实验数据GNSS站点分布如图 1所示.

图1 徐州地区GNSS测站点分布Fig.1 Distribution of GNSS stations in Xuzhou
实验数据利用GAMIT/GLOBK软件进行解算,以同步单天时段为单位进行,采用GPS和精密星历组合方式进行基线解算,最终得到全天候各测站的PWV,各参数配置如表 1所示.

表1 GAMIT参数配置
在进行插值运算前,首先对数据进行预处理,对徐州地区6个GNSS测站观测数据进行空间自相关分析,探究各GNSS测站的PWV与λ1(该测站到探空站的距离)、λ2(该测站的水汽密度)和λ3(该测站的水汽压)3个参数的相关性.通过单点定位的方式获取各测站坐标,根据欧氏距离计算公式解算各测站到探空站的距离.大气中的水汽绝大部分位于对流层,但它在垂直方向上随着高度的升高迅速减小[15],在研究地区GNSS地表测站数据中,统一选择地面最低起始高度处的水汽压和水汽密度数据,用相关系数度量2个变量X(各GNSS测站PWV)和Y(λ1,λ2,λ3)之间的相关性.通过表 2发现各测站PWV与距离相关性最大且干扰因素较少,而与水汽密度和水汽压相关性接近,且受其他水汽参数影响较大,故本文针对上述结果提出2种对PWV插值方法的优化策略.

表2 各采样站点PWV与λ1,λ2,λ3相关性
2.2 顾及水汽特性及其变化程度的优化策略
根据2.1实验,PWV与水汽压、水汽密度相关性接近,且受水汽分布影响较大,因此提出顾及水汽特性及其变化程度的优化策略.PWV可由天顶湿延迟(Zenith Wet Delay,ZWD)转换得到[16],ZWD主要受信号传播路径上水汽含量的影响,其中包括水汽密度和水汽压.
PWV=Π×ZWD,
(4)

(5)
式中,Π为无量纲水汽转换系数,ρv为液态水的密度,其值为1 g/cm3,Rw为水汽的气体常数,k′2,k3为转换系数,ZWD通过GAMIT高精度GNSS数据处理软件获取.

(6)
Tm=a+bTs,
(7)
式中,Tm为大气加权平均温度,e为水汽压,Ts为绝对温度.
通过上述公式可知,计算PWV需要已知Tm数值,本实验采用王明华[17]建立的中国区域统一模型与各单站的Tm-Ts线性模型,但Tm模型计算值与参考值的偏差随着季节不同有明显变化[18].
本实验基于徐州地区2017年5月1日前3天的探空站数据,将水汽密度和水汽压分别强制约束为某一值,建立先验水汽场,通过该水汽场给定Tm模型3个初始值进行约束,增加模型解算结果的稳定性,从而提高水汽场的反演精度,得到高精度的PWV,为GNSS站间距离优化做准备.
2.3 顾及GNSS站间距离的优化策略
由相关性分析实验可知,λ1(测站到探空站的距离)是3种参数中对PWV插值精度影响最大的因子,只受空间分布的影响,因此提出顾及GNSS站间距离的优化策略.根据IDW的数学特性,采样站点距离与插值精度有关[19],且距离权重函数与采样点到观测点的距离次幂成反比[20].本次实验采样站点距离探空站由近及远依次是:TSG0、HJG0、DSH0、TUG0、CHG0、SHG0.为确定哪几个测站的联合插值精度最高,依据采样点距离相关性依次减少测站数来设计实验,各个实验测站数量和位置如图2所示.

图2 各方案测站数量和站点分布Fig.2 Number of stations and station distribution map for 4 schemes
本次实验比较不同插值方法计算得出的最大值、最小值、平均值和标准偏差4项指标.根据表 3,表明方案B:TSG0、HJG0、DSH0、TUG0、CHG0这5个测站插值效果最佳.
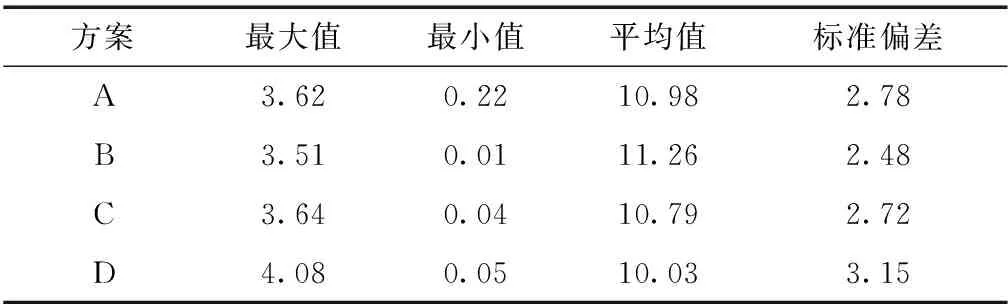
表3 不同个数采样站点插值效果统计
本实验利用徐州地区采样站点分布不均的空间特性,对IDW插值参数优化,并基于本地区的先验信息加以约束,提出了顾及GNSS水汽特性和站间距离的优化IDW插值方法.具体过程如下:
1)基于实验数据前3天的探空站水汽密度和水汽压数据建立先验水汽场,对Tm模型附加初值进行
约束,对IDW参数优化;
2)对方案B的5个测站进行反距离权重插值,在以格点为中心的360°方位上,改变搜索椭圆的长短半径,使其全部覆盖实验区,实验区不规则时可将搜索椭圆旋转一定角度;
3)平均划分成4个象限,在每个象限区选择测站点,每个象限都有站点数据参与插值;
4)优化幂参数,将p从2到10分别实验,通过交叉检验比较插值误差大小,基于基础数据,取p为5.875 474 8时,插值误差较小.
3 结果分析
本文插值检验主要采用交叉验证的方法来对比分析插值结果,即假定一个已知气象站点的数据未知,使用其他气象站点的实测值来估算该点的数据,并进行误差分析.研究过程中采用标准差(Standard Deviation,SD)、平均相对误差(Mean Relative Error,MRE)、平均绝对误差(Mean Absolute Error,MAE)及均方根误差(Root Mean Square Error,RMSE)作为评估插值方法精度的标准.
3.1 插值方法精度分析
本文采用线性插值三角网法(方法1)、IDW插值法(方法2)、Kriging插值法(方法3)和顾及GNSS水汽特性和站间距离的优化IDW插值方法(方法4)4种插值方法对数据进行计算.
以往的观测实验表明,PWV与局地降水存在密切的关系,每次降水过程都对应着PWV的迅速增加[21].由图 3可知,徐州地区大气可降水量总体呈现西北至东南逐渐增加的空间格局,西北少、东南多,梯度变化较为明显,PWV值相差较大.不同插值方法所得结果在色彩平滑程度以及局部地区的空间分布上存在一定差异:方法3和方法4色彩过渡较为强烈,而方法2的插值结果较为平滑,但基于所选数据为突降暴雨前,说明采用方法4对徐州地区PWV进行插值,能够减弱采样站点分布不均及大气总水汽量激增的误差.
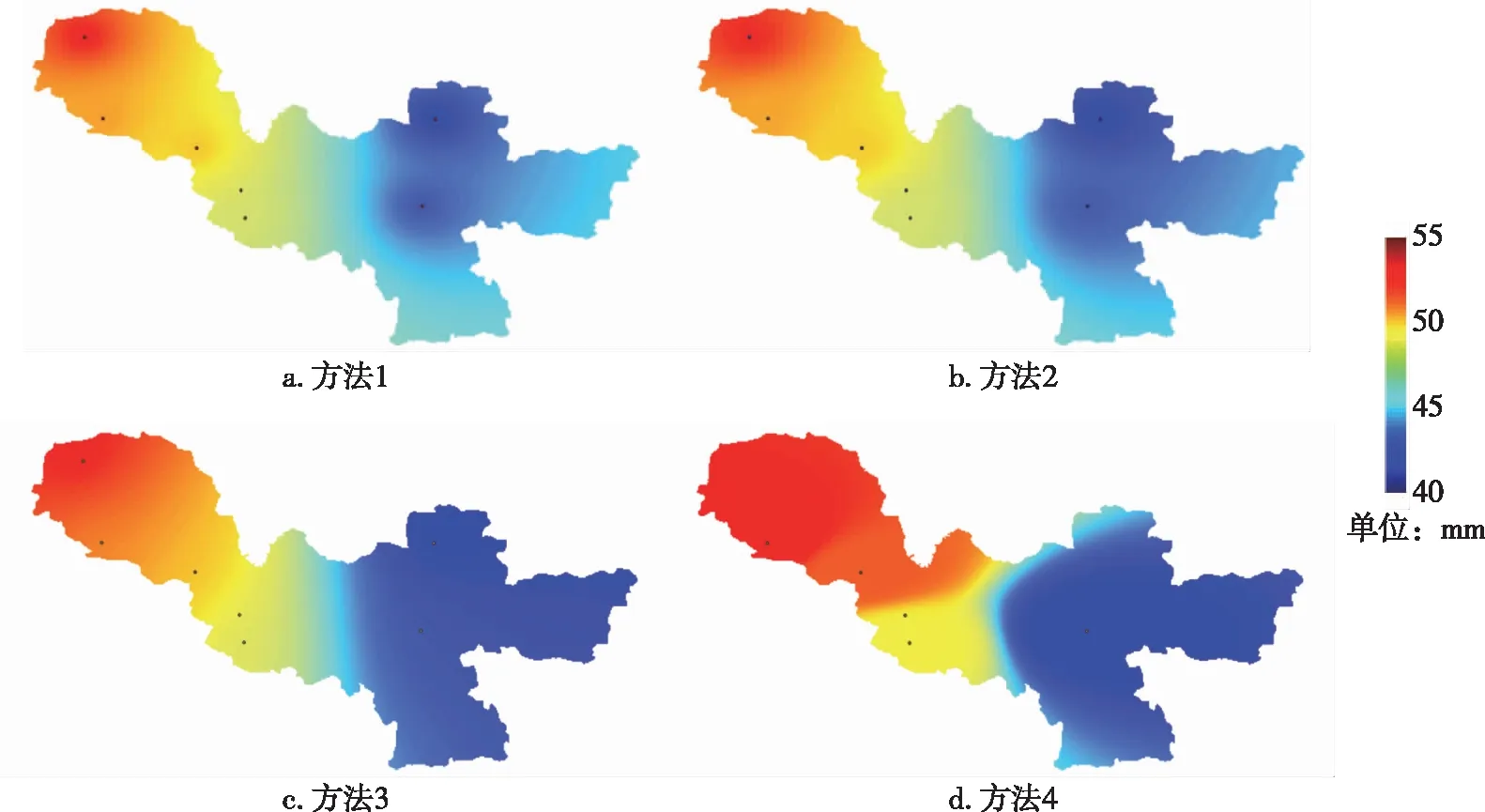
图3 4种不同插值方法的色彩Fig.3 Color images of four interpolation methods a.linear interpolation triangulation;b.Kriging interpolation;c.IDW;d.the improved IDW interpolation
3.2 与探空站数据对比
本次实验采用SD、MAE、MRE、RMSE作为评估插值方法精度的标准,将徐州地区探空站每天UTC12:00的数据作为参考标准,对4种插值方法进行精度评定.由表 4可知:方法4的SD数值较小,数据集分布较均匀;相较传统的IDW插值方法(方法2),方法4的MAE和MRE分别提高了19.48%、19.16%.RMSE可以反映误差分布大致情况以及误差在基准线的集中程度,表4表明方法4误差较集中,其RMSE较方法1、方法2、方法3分别提高了14.88%、15.70%、4.12%.

表4 4种不同插值方法计算误差交叉验证结果
进一步对比不同插值方案反演PWV误差的大小,以探空站数据为参考值对各插值结果求残差值,并绘制箱型图.由图 4可以看出,4种方法的误差对应的箱形图具有自身的特点,线性插值三角网法和IDW方法具有的异常值数值较大,离散程度也较大,而Kriging和优化IDW插值方法的异常值较小,也较集中.箱形图各个层上优化IDW插值方案的误差分布较其他方案更为集中,残差数据较小.

图4 4种不同插值方法的箱形图Fig.4 Box-plot of four interpolation methods
4 结语
本文提出顾及GNSS水汽特性和站间距离的优化IDW插值方法,基于徐州地区的先验信息,比较分析GNSS大气水汽特性与站点间距离对插值结果的影响,对插值参数进行优化,主要结论如下:
1)在3种传统插值方法中,插值精度的RMSE值均超过3.5 g/m3,其中线性插值三角网法与IDW插值法的插值精度较低.与传统算法相比,本文所提出的顾及GNSS水汽特性和站间距离的优化IDW插值方法能够有效改善插值结果的质量,其RMSE值为3.49 g/m3,而稳定性方面,新方法的误差分布相较3种传统方法更加集中,且异常值也较少.
2)在大气总水汽量激增的情况下,该方法反演的三维水汽色彩图更能反映真实情况,结合表4可知拟合后探空站位置处的插值精度较高.大气总水汽量激增常伴随着降水过程的发生,此时水汽含量不同区域PWV分界明显,在图上表现为色彩过渡强烈,表明该方法能够减小采样站点分布不均及大气总水汽量激增带来的误差.
3)新方法反演大气水汽可适用于GNSS站网布设较为稀疏的地区,采用该方法能够在计算结果上减弱大气可降水量平均值的影响,有效提高大气水汽时空分辨率精度,估值准确率高.该方法基于一个地区的先验信息,通过对其地区GNSS大气水汽特性和站网间距离统计分析,对IDW参数优化,有效提高了插值精度.
