脉动热管温度时间序列的关联维分析
2022-06-11周屹杨洪海张苗
周屹 杨洪海 张苗
东华大学环境科学与工程学院
脉动热管(Pulsating Heat Pipe,PHP)是一种新型的高效换热元件,具有传热效率高,结构简单[1]等优点。目前国内外对PHP已有广泛的研究。脉动热管虽然结构简单,但其内部的传热过程复杂,实验方面,主要是从工质,充液率,倾斜角[2]等方面进行研究。理论方面,C heng和 Ma[3]通过汇总理想状态气体方程和热力学第一定律,得到了液塞和气塞的质量 -弹簧-阻尼模型。理论模型对管内工质的状态和运行都进行了一定的简化,无法真实的反应管内流体的运动状态,对于这种系统可以采用非线性理论进行研究。宋延熙[4]等通过关联维,H urst 指数等非线性分析方法表明,脉动热管内的温度波动是确定性混沌运动。Q u[5]等使用李雅普诺夫维数等一系列判别混沌方法,表明脉动热管的弱混沌特性。方海洲[6-7]等运用功率谱,H urst指数,小波分解等非线性分析方法,发现温度信号波动属于分形下的混沌行为。以上对温度时间序列的分析,均测量的是管壁温度。虽然铜管的导热系数高,但导热的延迟不可忽视,因此,本文搭建脉动热管可视化试验台,并测量管内的流体温度进行关联维分析。
1 实验系统
本实验的实验系统由脉动热管,电加热系统,冷却系统和温度采集系统等组成。实验装置图则由图 1所示。
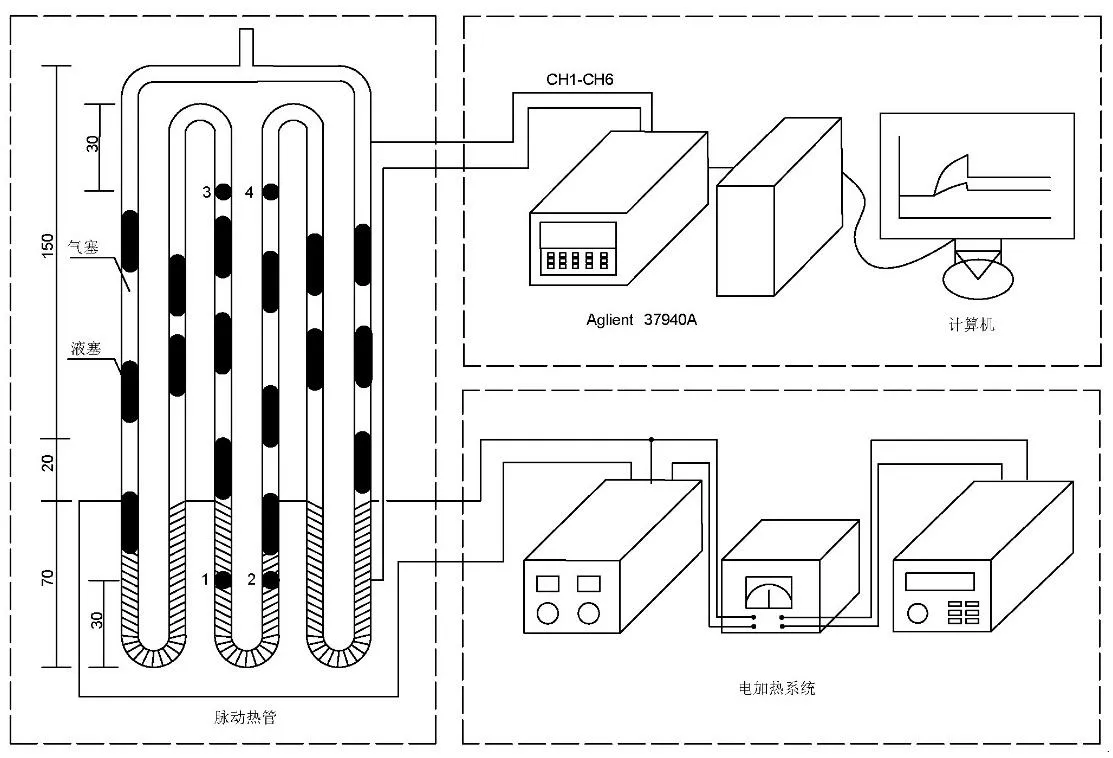
图1 实验装置图
脉动热管采用石英耐热玻璃弯折而成,内径2.5 mm,外径 4 mm,总高度 240 mm,其中蒸发段70 mm,冷凝段150 mm,绝热段20 mm。蒸发段均匀的缠绕电热丝,通过直流电源(MP1203D)进行加热,冷凝段置于风管中进行强制冷却。为了减少散热,将蒸发段整体置于一方盒子中,四周缝隙用密封胶进行密封,除此之外,在方盒子的内壁面采用铝箔反射膜-珍珠棉(6 mm)-铝箔反射膜的三层保温结构。总计使用了6个K型热电偶,测量精度为±0 .1 ℃,1号和2号测量蒸发段管内流体温度,3 号和 4 号测量冷凝段管内流体温度,5号在保温层内侧,6号在保温层外侧。
在实验前为了充液以及排除管内的不凝性气体,需要对脉动热管进行抽真空处理,当真空度达到 1.5× 10-3Pa时,保压15分钟后进行充液,充液率为55%。温度由Aglient 34972A进行采集,扫描频率为20 Hz。
详细实验工况见表1。
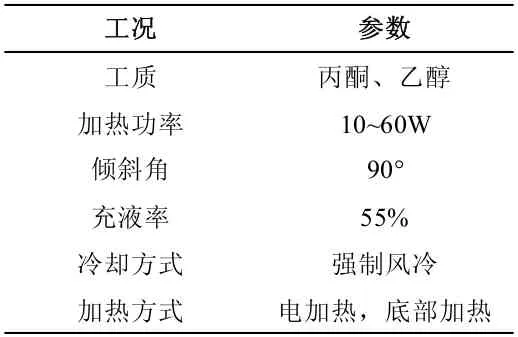
表1 实验工况
2 关联维方法
2.1 关联维
分形理论是描述混沌信号的一种手段,分形是没有特征长度但具有一定意义的自相似图形的总称,最初由 Mandelbrot 在研究海岸线等不规则曲线时提出,之后人们发现自然界普遍存在分形现象。分形的主要特征是自相似性,即局部与整体存在某种相似性,混沌的奇怪吸引子具有不同于通常几何形状的无限层次的自相似结构,这种几何结构可以用分形维数来描述[8-9]。现已有许多分形维数的定义和计算方法,本文使用关联维数D2计算分形维数。
1983 年,G rassberger 和 Procaccia[10]提出了一种估算D2的经典算法,其算法一般简称为 GP算法。具体步骤如下:
1)估计时间序列x(i)i=1,2,……,N的时间延迟τ和嵌入维数m,等到重构相空间X(i)
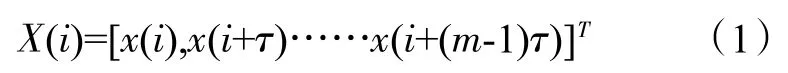
式中:i=1,2,……,M,M=N-(m-1)τ。
2)计算关联积分
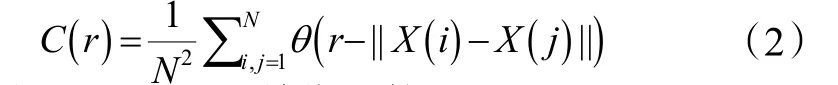
式中:θ(x)是Heaviside单位函数。
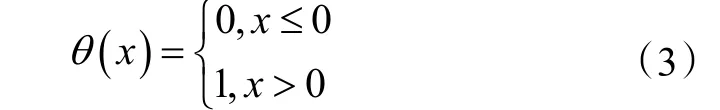
||X(i)-X(j)|| 定义了矢量X(i)与矢量X(j)之间的距离。
3)在r的无标度区域内,双对数曲线ln(r)~ln(C(r))满足线性关系,线性区域的斜率即为D2。

2.2 参数选取
在使用G-P算法计算关联维时,嵌入维数m和延迟时间τ的参数选取极为重要。延迟时间过小,信息不容易显示。延迟时间过大,则坐标值x(n)和x(n+τ)相互之前的动力学联系不能展现。有很多种方法可以确定延迟时间,自相关函数法和互信息法[11]是常用的两种方式。
Lorenz系统由Lorenz于 1963年提出,由如下常微分方程组描述:
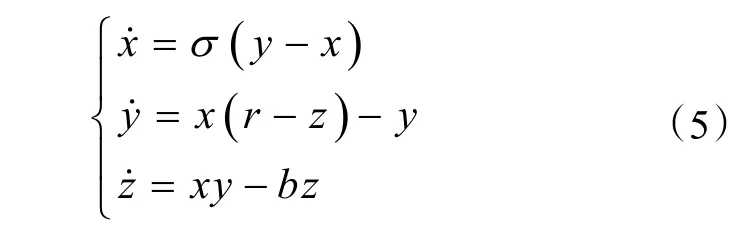
式中:x,y,z均为时间t的函数,参数σ=10,r=28,b=8/3初值取[x,y,z]=[0,1,0],积分步长为0.01。
取 Lorenz 吸引子x分量的前 5000 个点为例,进行计算。图 2为计算结果。

图2 Lorenz吸引子x分量的自相关函数和互信息
取自相关函数下降到初始值的 1-1/e 或互信息的第一个极小值点作为最优延迟时间,根据计算数据,Lorenz吸引子x分量的延迟时间取12。
嵌入维数m采用饱和关联维方法[12]来确定,即逐步增加嵌入维数,直到无标度区域的斜率维持在一个常数时,将此时的m作为嵌入维数。
2.3 Lorenz吸引子x分量的关联维
图3是Lorenz吸引子x分量的双对数曲线,嵌入维数m取1~10。从图4可以看出,在m≥6之后,此时的斜率不再变化,曲线收敛,关联维D2基本稳定在2.1左右,标准值D2为2.06[11]。
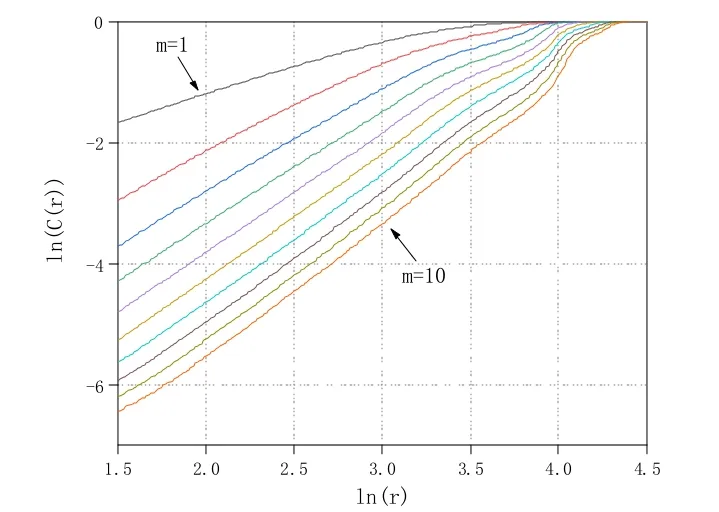
图3 Lorenz吸引子x分量的双对数曲线
3 结果与讨论
3.1 温度时间序列分析
本实验的脉动热管由玻璃制作,可以直接观察到管内的工质流动情况。随着加热功率的提升,脉动热管可以大致分成三种运动状态。一种是在低加热功率时,管内液塞几乎不运行。二种是在中等加热功率时,管内流体小幅震荡,但仅限在同一根管的蒸发段和冷凝段之间运行,并不会越过弯头进入相邻管。三种是在高加热功率时,管内工质形成整体的循环流动。基于三种运动状态,可以对应的将加热功率大致分为10 W 为低加热功率,20~30 W 为中等加热功率,40~ 60 W为高加热功率。
图5是丙酮作为工质运行时的温度时间序列图,可以看出不同运动状态对应的温度时间序列的特征。低加热功率时,温度会较长时间的稳定在某一温度,即管内工质不流动。高加热功率时,温度波动的具有一定规律性,频率较高,也可以说明管内工质在高加热功率是运行速度较快。
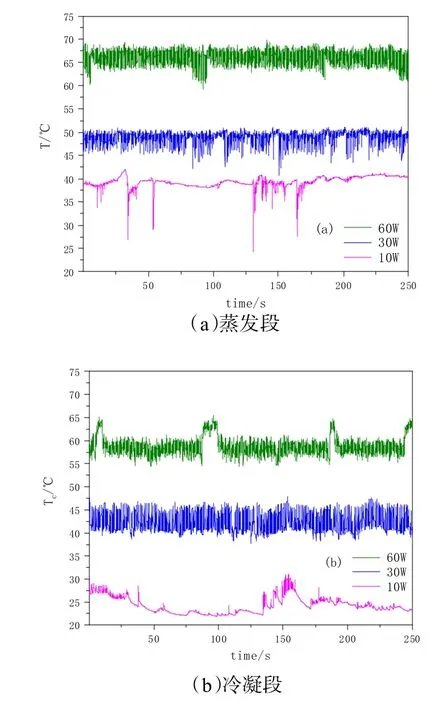
图5 丙酮温度时间序列图
图6是乙醇作为工质运行时的温度时间序列图,首先可以发现上文对运动状态的分类也适用于乙醇脉动热管。除此之外,从图中可以看出丙酮整体的运行情况比乙醇好,原因在于:一是,当加热功率为60 W时,两种工质的冷凝段温度都在60 ℃左右,但丙酮的蒸发温度更低,说明在同等冷却方式下,丙酮带走了更多的热量,热阻更低。二是,当加热功率为30 W时,丙酮和乙醇都不处于整体运动状态,但丙酮温度波动频率高于乙醇,说明在中等加热功率是,丙酮在单管内的换热强于乙醇。三是,当加热功率为 10 W时,乙醇和丙酮均未启动,可以观察到丙酮出现非周期性的温度波动,原因在于虽然加热功率小无法产生足够的压差使液塞运动,但经过一段时间的热量积累,液塞会被冲到冷凝段,冷凝段低温的液体运动到蒸发段。这种运动并不能持续进行,这也是温度序列中间歇性波动的原因。
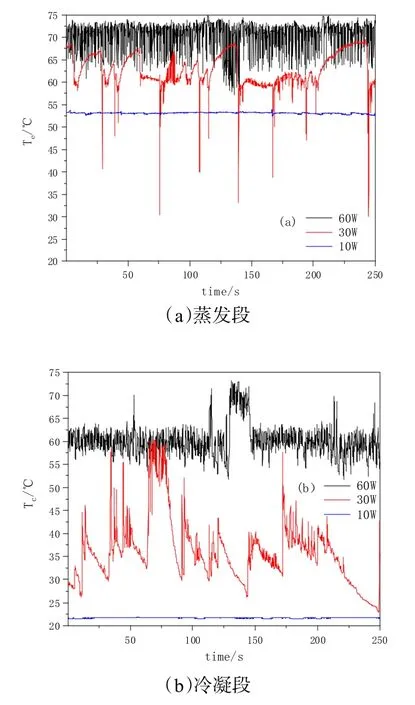
图6 乙醇温度时间序列图
3.2 加热功率对关联维的影响
图7为丙酮为工质,热端和冷端在不同加热功率下关联维随嵌入维数的变化趋势。从图中可以看出,随着嵌入维数的增加,关联维数也不断增加,并趋于饱和,图中虚线表示关联维的饱和值。在不同加热功率下,饱和关联维值明显不同,存在明显的分界。10 W时温度序列比较平稳,关联维较小,随着加热功率的增大,温度序列的波动更加剧烈,非线性程度也发生了变化,60 W时,关联维达到最大,这表明 PHP 系统的复杂性也在随加热功率增加。此外,发现相同加热功率下,冷凝段的关联维均小于蒸发段的关联维,表明蒸发段温度波动更加复杂,Q u也发现同样的趋势。
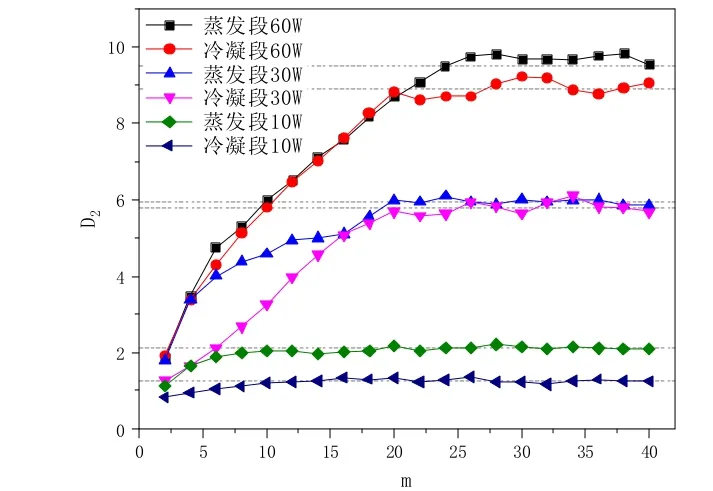
图7 丙酮关联维D2随嵌入维数m的变化
图8为乙醇在不同加热功率下随嵌入维数的变化趋势,可以发现与丙酮类似的结论。除此之外,在 30 W和60 W时,丙酮的关联维值均小于乙醇的关联维值,可以表明管内丙酮的运动比乙醇更加剧烈,温度波动的频率更高,幅度更小,丙酮的传热性能也优于乙醇。
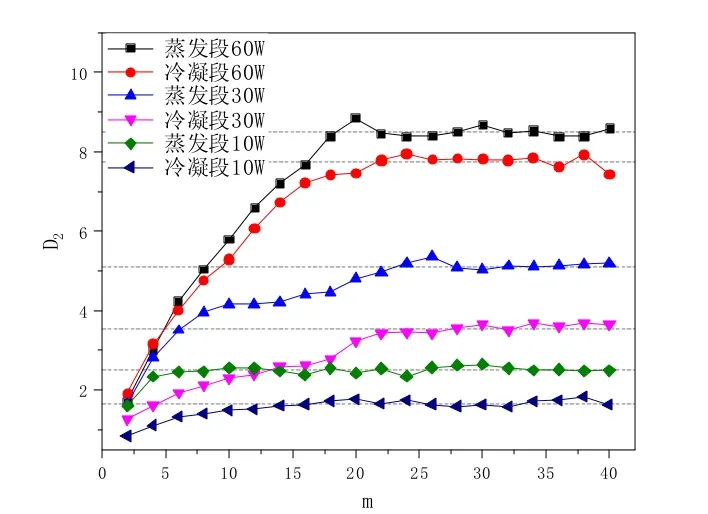
图8 乙醇关联维D 2随嵌入维数m的变化
以丙酮为工质,蒸发段的饱和关联维为9.545,冷凝段的饱和关联维为8.902,要大于方海洲[7]的计算结果。以乙醇为工质,蒸发段的饱和关联维为8.509,冷凝段的饱和关联维为 7.75,关联维值也大于 Qu[5]的计算结果。表2是关联维计算的总结。这是由于测量方式的区别导致的不同,本文直接测量流体温度,而其他文献测量的均为管壁温度,虽然铜管的导热系数大,但并不能真实反映管内流体的运动情况,这也是本文计算的关联维数值大于文献的原因。
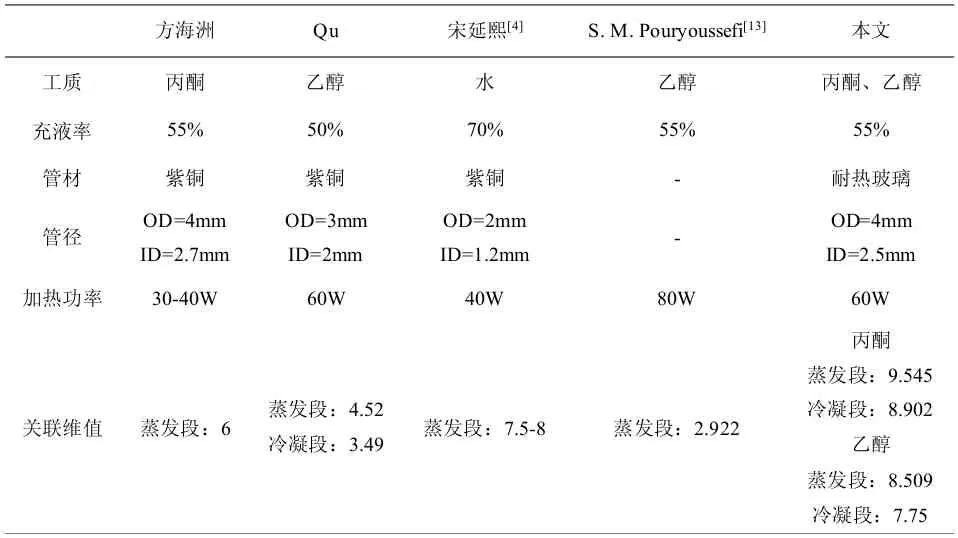
表2 关联维计算总结
3.3 关联维对传热的影响
图9给出了不同加热功率下,丙酮脉动热管蒸发段温度的关联维和热阻曲线。从温度波动曲线和热阻图可知,热阻与关联维成反比关系。丙酮脉动热管在20 W时已经热阻已经降至0.3,观察到管内工质在此时已经在快速小幅震荡,虽未形成循环流动,但传热能力相比于10 W已经大大加强了。与此相对应的是关联维的值也有了较大的跃升,这表明随着脉动热管传热能力的增强,管内的相变换热愈发剧烈,气泡的生成频率增加,整体的复杂性突升。当处于高加热功率时,此时脉动热管内部已经形成循环流动,关联维和热阻随加热功率的变化幅度变小,关联维基本维持在 8~9 左右,由关联维的物理意义可知,此时如要准确表述脉动热管运动情况,至少需要9个变量,例如工质的表面张力,气化潜热,与壁面接触角,充液率等。
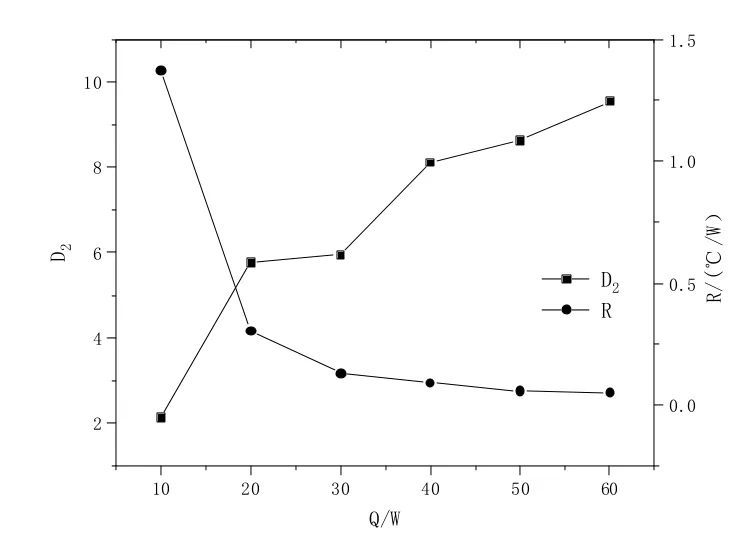
图9 加热功率对关联维和热阻的影响
4 结论
本文设计了脉动热管可视化试验台,以丙酮和乙醇为工质,采集管内流体温度进行了非线性分析,结论如下:
1、以丙酮作为工质的脉动热管运行情况要优于乙醇。
2、关联维D2随嵌入维数m的增加而增加,m增大到一定值后,关联维趋于收敛。
3、蒸发段温度的关联维略大于冷凝段温度的关联维。
4、相比采集壁温信号,管内流体的温度信号更能准确反映管内的运动状态。
5、热阻与关联维成反比关系,如要准确描述循环流动的脉动热管,至少需要 9个变量。
