基于能耗模拟的被动房外墙保温厚度优化
2022-06-11张浩杰郝小礼殷维2胡锦华
张浩杰 郝小礼 ,2*殷维 ,2胡锦华 ,2
1湖南科技大学土木工程学院
2湖南省智慧建造装配式被动房工程研究中心
0 引言
被动房在建造过程中使用了较厚的保温材料,使得运行过程中的能耗、碳排放和成本减少的同时,导致其建造过程中能耗、碳排放和成本增加。所以,如何量化被动房的保温层厚度,提高建筑全生命周期的节能减排效果,具有重要的实际应用价值。
现有研究多数为单一目标优化,可以直接得到唯一优化结果。然而现实问题往往目标不是单一的,而且各目标之间可能会相互冲突。因此对于多目标优化问题,往往不能得到唯一解[1]。现有关于保温层厚度的多目标优化研究,多数只能给出一个取值范围,往往不利于使用者决策。针对此类问题,结合全生命周期理论,提出一种新的基于遗传算法的分层次多目标组合优化分析方法,并得到基于多个目标的最佳保温层厚度唯一解。
1 数学模型及分层多目标优化方法
1.1 目标函数模型
1.1.1 全生命周期能耗
建筑全生命周期能耗是建材生产运输过程,建筑建造过程,建筑运行过程和建筑拆除处置过程的能耗总和。为消除不同能源种类品质上的差异,将不同种类的能源消耗转换成一次能源(标准煤)之后,再进行求和。同时,为消除建筑规模大小对生命周期能耗的影响,采用单位建筑面积的生命周期能耗作为评价指标。由于主要考虑保温材料厚度的优化问题,只有保温材料厚度是变量,因此不考虑建筑本体材料的生产运输和安装能耗,对优化结果没有影响。可用式(1)~(3)计算。

式中:LCE、E1、E2、E3、E4分别为单位建筑面积全生命周期能耗、外墙保温材料的生产运输能耗、保温施工过程的能耗、所需的年运行能耗、拆除处置过程的能耗,kWh/m2;N为建筑的运行年限,年 ;对于正常使用和维护,保温材料的使用年限一般为 20~30 年[2],本研究取20年;ρ为建筑外墙保温材料的密度,kg/m3;S0为建筑安装保温材料的外墙总面积,m2;d为建筑外墙保温材料的厚度,m ;E0为单位质量保温材料的生产运输能耗,M J/kg;S为总建筑面积,m2;Eh、Ec、Eq为单位建筑面积年供暖能耗、年供冷能耗、年其它能耗(包括照明、设备、热水等),kWh/m2;fh、fc、fq分别为相应能源的一次能源转化系数,电力取2.6,燃气、燃油取 1。建筑建造工程与拆除处置阶段中的相关数据难以获得、且对全生命周期能耗的影响很小[3],因此忽略建筑建造过程和拆除处置过程的能耗,只考虑保温材料的生产运输能耗及建筑运行能耗。
1.1.2 全生命周期碳排放
建筑全生命周期碳排放是建材生产运输过程,建筑建造过程,建筑运行过程和建筑拆除处置过程的碳排放总和。同样只考虑保温材料的生产运输过程中的碳排放,可用式(4)~(6)计算。
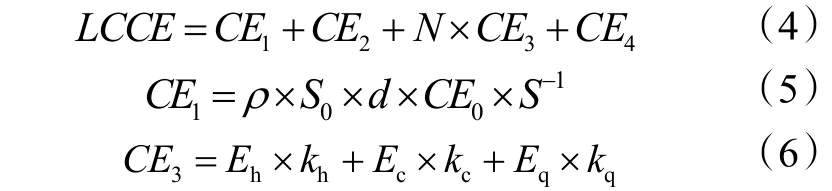
式中:LCCE、CE1、CE2、CE3、CE4分别为单位建筑面积全生命周期 CO2排放、外墙保温材料生产运输过程的CO2排放、外墙保温施工过程中的CO2排放、所需的年运行 CO2排放、拆除处置过程 CO2排放,kg/m2;CE0为单位质量的保温材料在生产运输过程产生的 CO2排放,kg/kg;kh、kc、kq分别为相应能源的碳排放系数,kg/kWh;空调设备为带新风热回收的空气源热泵,使用的能源为电力。根据生态环境部文件,2015 年全国电网平均碳排放因子为0.6101 kg/kWh[4]。其余符号的意义与前面相同。同样,因为建筑建造工程与拆除处置阶段中的相关数据难以获得,且对全生命周期碳排放的影响很小[3],所以忽略建筑建造过程和拆除处置过程的碳排放。
1.1.3 全生命周期总成本
建筑全生命周期总成本是建材生产运输过程、建筑建造过程,建筑运行过程和建筑拆除处置过程的经济花费总和。与前面相同,只考虑保温材料的相应花费。可用式(7)~(9)计算。

式中:LCC、C1、C2、C3、C4分别为单位建筑面积全生命周期总成本、外墙保温材料的生产运输成本、外墙保温施工过程的成本、所需的年运行成本、拆除处置过程成本,元/m2;C0为单位质量保温材料的生产运输成本,元/kg;Ph、Pc、Pq为对应的能源价格,元/kWh。研究采用考虑了煤电外部成本后的综合电价[5],0.88 元/kWh;ζ为考虑了资金时间价值后的计算系数,用下式计算:

式中:r为利率,r=2.1%;i为通货膨胀率,i=1.5%[6]。同样,由于外墙保温施工过程和拆除处置过程花费相对较少,计算过程中也忽略。
可以看出,全生命周期能耗,全生命周期碳排放和全生命周期总成本与保温材料的物性参数有关。本文以EPS 板作为墙体保温材料,进行分析。EPS 板的部分材料参数[7]见表1。

表1 EPS材料参数
1.2 优化方法
1.2.1 单目标优化
单目标优化是指运用全生命周期优化理论,分别计算不同保温层厚度下的全生命周期能耗、全生命周期碳排放、全生命周期总成本,所得结果的极小值对应的保温层厚度,即为单个目标函数下的最优保温层厚度。但是对于决策者来说,到底选择哪个值作为最终实施方案难以决策。如果只考虑单个目标则具有单一性、片面性,会影响决策的代表性,因此需要对多个目标函数进行综合考虑,耦合优化。
1.2.2 分层多目标优化
人们会经常会遇到需要使多个目标在给定区域内同时都尽可能最佳的优化问题。各个子目标之间是矛盾的,而只能在它们中间进行协调和折中处理,使各个子目标都尽可能地接近最优化。
研究考虑了3 个目标函数,这本质上是一个多目标非线性优化问题。为得到该优化问题的唯一解,提出采用分层多目标优化的方法,该方法计算流程如图1所示。即:先选取两个目标函数,运用 NSGA-II算法进行两目标综合求解,得到 Pareto 前端,在这一组非劣解集(Pareto解)中,进行另一个目标的计算,求其最优点。NSGA-II是最流行的多目标遗传算法之一[8],是一种全局搜索算法,运行速度快,解集收敛性好。Deb等[9]提出的带精英策略的非支配排序遗传算法(NSGA-II)适用于解决复杂的多目标优化问题,其算法流程如图2所示。
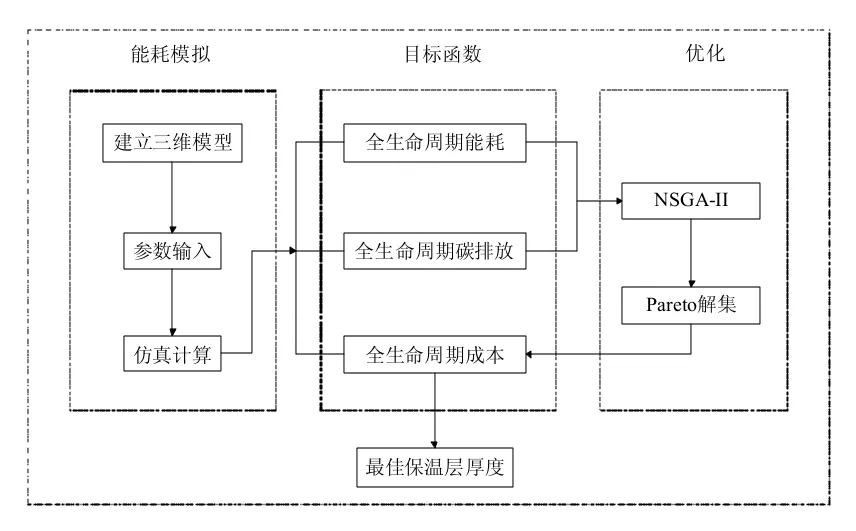
图1 优化计算流程图

图2 NSGA-II算法流程图
为验证本方法的可行性,下面以实际建筑为例,介绍本多目标优化方法的实施过程和优化结果。
2 能耗模拟
2.1 物理模型
以湖南省株洲市某被动房住宅项目为依据。建筑占地面积为22亩,共四栋,每栋建筑地上 12 层,地下1层,地下为车库,地上每层4 户,共 192户,图 3是该项目的实物照片。选取了其中第二栋作分析,其位置如图4所示。优化都是建立在建筑能耗模拟的基础之上的,选取的能耗模拟软件为DesignBuilder[10]软件。是在EnergyPlus的基础上,开发的一款综合用户图形界面建筑能耗模拟软件。建立建筑的三维数字模型,如图5所示:

图3 模拟建筑实物照片
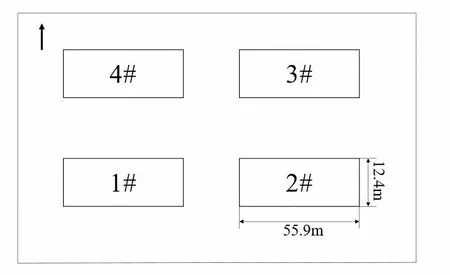
图4 模拟建筑位置示意图
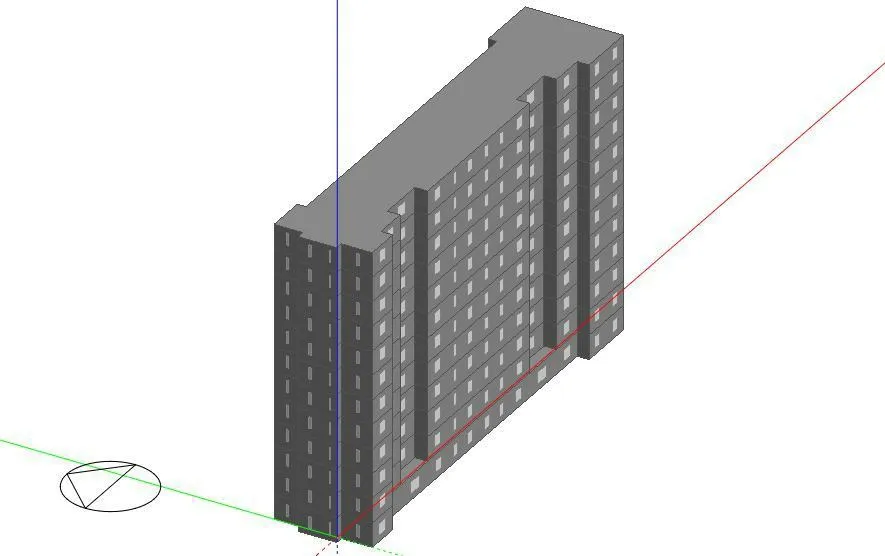
图5 建筑模拟模型
1)围护结构热工参数。在软件DesignBuilder里进行参数设置,建筑本体主要材料及相关物性参数见表2,窗墙比东南西北别为0.16、0.16、0.05、0.13。

表2 建筑本体材料及物性参数
2)室外气象参数。研究对象位于中国湖南省株洲市,属于典型的夏热冬冷地区,典型年室外气象参数按照EnergyPlus气象数据库选取,来源为CSWD。
3)室内热扰及作息安排。人员,设备,照明,空调及生活热水参数设置参考 GB50736-2012[11]和GB/T51350-2019[12]规定取值见表3。假设相同功能房间人员活动规律基本一致。以满足每人每小时 30 m3新风量为原则,室内通风作息与人员作息设置相同。建筑暖通空调系统采用定风量系统,冷热源采用空气源热泵直膨式机组,添加新风热回收装置,全热回收率65%。规定空气渗透换气次数为0.07 h-1。

表3 人员、设备及照明参数
2.2 能耗模拟计算
考虑被动式建筑的气密性和保温性能等特点,同时为维持全年舒适的环境,实施全年 8760 h 不间断供暖、供冷的空调模式。除楼梯间、电梯间以外,各房间保证在供暖期间室内温度维持在 19-20 ℃范围内,相对湿度在30%以上。房间保证在供冷期间室内温度在维持在26-27℃范围内,相对湿度在 60%以下,由温湿度智能控制房间的供冷、供暖时间。
利用建立的建筑模型和室内外参数设置,模拟得到当保温材料(EPS 板)厚度为 160 mm时的运行能耗,结果如表4所示。

表4 建筑能耗结果
由模拟结果可知,一次能源消耗为 103.51,小于要求的120,满足被动房技术要求。同时说明计算结果可信,可以用该建筑模型进行全生命周期运行能耗模拟分析。
3 结果与讨论
利用被动房建筑模型,结合全生命周期能耗、全生命周期碳排放、全生命周期总成本三个目标函数的计算模型,建筑保温层厚度在 0~300 mm范围内变化,按照10 mm为间隔步长,计算不同保温层厚度下的全年能耗,分别得到单目标和多目标条件下保温层厚度的量化结果。
3.1 单目标优化结果
3.1.1 全生命周期能耗结果
如图6所示,保温材料厚度的增加,单位建筑面积所需外墙保温材料的生产运输能耗呈现线性增加的规律。单位建筑面积的年运行能耗随保温层厚度的增加,先显著下降,但下降的速率随厚度的增加逐渐减小,达到某一厚度之后,运行能耗反而随保温层厚度的增加而略有增加。这个增加的幅度很微小,主要是由于夏热冬冷地区的气候特点造成的。在这一地区,有较长的过渡季节,如果使用的保温材料厚度过大时,反而不利于过渡季节室内多余的热量散发到室外,增加了空调系统开启的时间,从而会导致过渡季节运行能耗增加。对于夏热冬冷地区,并不是保温层越厚,运行能耗越小。

图6 生产能耗,运行能耗与保温厚度关系
从图 6 还可以看出,增加保温层的厚度,单位建筑面积所需外墙保温材料的生产运输能耗是增加的,但单位建筑面积所需的年运行能耗却基本是降低的。而建筑的生命周期能耗其必定存在一个最优的保温层厚度,使得生命周期能耗最小。如图7所示,在使用EPS板时,考虑使用年限为 20 年,则建筑全生命周期能耗最低的保温材料厚度为110 mm。
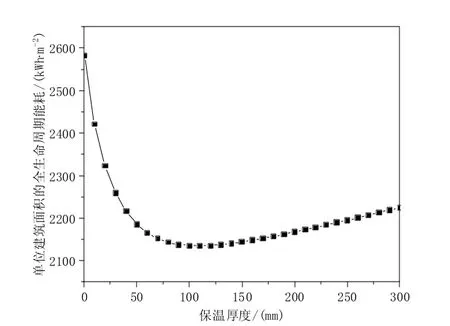
图7 全生命周期能耗与保温厚度关系
3.1.2 全生命周期碳排放结果
如图 8 所示,随着保温材料厚度的增加,单位建筑面积所需外墙保温材料的生产运输过程碳排放呈现线性增加的规律。而单位建筑面积所需的年运行碳排放随保温层厚度的增加,先显著下降,但下降的速率随厚度的增加逐渐减小,达到某一厚度之后,运行碳排放反而随保温层厚度的增加而略有增加,这个增加的幅度很微小。导致运行碳排放随保温层厚度增加呈现先降后升的规律的原因与前面解释的运行能耗变化规律的相似,不再赘述。
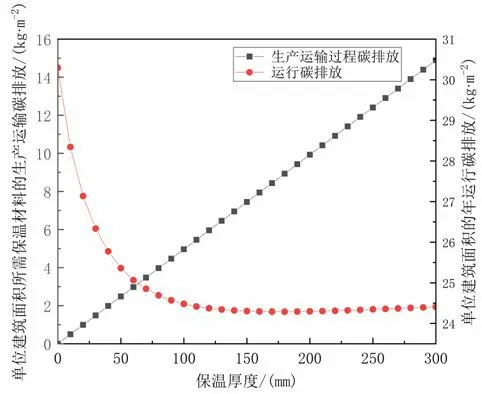
图8 材料碳排放,运行碳排放与保温厚度关系
从图8可以看出,建筑保温材料厚度的增加对于建筑的生产运输碳排放和建筑的运行碳排放的影响同样具有矛盾性。因此,对于建筑生命周期总碳排放,也同样存在一个最优的保温层厚度,使得生命周期碳排放最小。从图9中可以看出,在使用EPS板时,考虑保温材料使用20年,则建筑全生命周期碳排放最低的保温材料厚度为130 mm。可见,保证生命周期碳排放最优的保温层厚度,并不能保证生命周期能耗最小。

图9 全生命周期碳排放与保温厚度关系
3.1.3 全生命周期总成本结果
图10 展示了单位建筑面积所需外墙保温材料的生产运输成本和单位建筑面积所需的年运行成本随保温层后的变化规律,其变化规律与能耗,碳排放随保温层厚度变化的规律相似。同样,也存在最佳的保温层厚度,使得全生命周期总成本最小。从图11可以看出,在使用 EPS 板时,如果保温材料使用 20 年,则建筑全生命周期总成本最低的保温材料厚度为110 mm。这个最优的保温层厚度不同于建筑全生命周期碳排放最少的保温层厚度,其数值上尽管与生命周期能耗最少的保温层厚度相等,但二者之间并没有必然性。
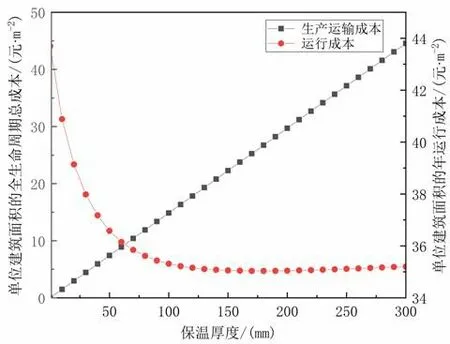
图10 材料成本、运行成本与保温厚度变化关系
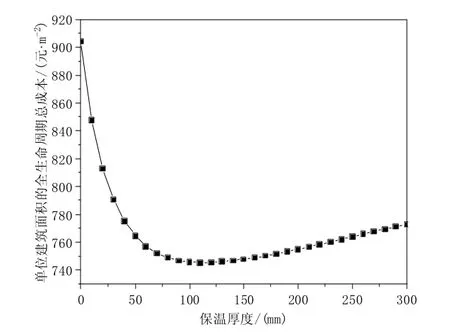
图11 全生命周期总成本与保温厚度关系
3.2 分层多目标优化结果
首先将能耗计算结果拟合成保温层厚度的函数,如图12所示,其拟合的R2=0.9987,表明能耗被很好地拟合了。进一步可以建立三个目标函数与保温层厚度之间的函数关系。选取其中的全生命周期能耗和全生命周期碳排放,使用 NSGA-II算法计算,获得的Pareto解集如图13所示,遗传算法的参数设置如表5所示。图13中,纵、横坐标轴展示的是无量纲标准化的碳排放和能耗,可按照式(11)计算。

表5 部分算法参数
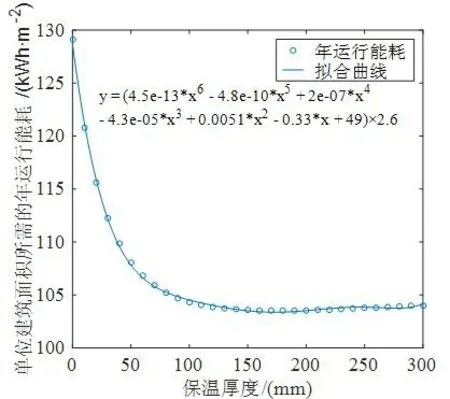
图12 年运行能耗与保温厚度关系拟合曲线
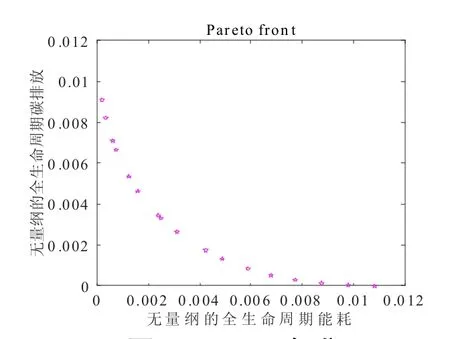
图13 Pareto解集

式中:yt为相应的无量纲化后的能耗或碳排放值;xt为相应保温厚度下的能耗或碳排放值;xmax为相应的能耗或碳排放最大值;xmin则为相应的能耗或碳排放的最小值。
最后,在 Pareto 解集中,求取全生命周期总成本最小的保温层厚度。表6显示了Pareto解集中的每一个元素对应的生命周期总成本计算结果,图 14的图形则显示了表6中,生命周期总成本与保温层厚度之间的变化规律。从图14中则可发现,多目标下的最佳保温厚度为120.74 mm,约为121 mm。所以,综合考虑生命周期能耗,生命周期碳排放和生命周期总成本,对于本优化条件,最佳的保温层厚度为 121 mm,显然,该厚度介于多个单目标优化结果之间,也从侧面说明了本文提出的最佳保温层厚分层优化方法合理有效。

图14 最佳保温厚度取值

表6 Pareto解集的成本计算结果
4 结束语
针对单目标优化的局限性,提出采用基于NSGA-II算法的分层多目标优化方法,以被动房保温层厚度为变量,针对全生命周期能耗、全生命周期碳排放、全生命周期总成本三个目标进行优化分析。以夏热冬冷地区某被动式住宅为例,基于全年能耗模拟的手段,通过先选取全生命周期能耗和全生命周期碳排放两个目标函数,运用 NSGA-II算法进行两目标综合求解,得到 Pareto 前端,然后在这一组非劣解集中,求取另一个目标—— 全生命周期总成本最优的点。对于采用EPS板作为保温材料,使用年限为 20年的情况,采用分层多目标优化得到的最佳保温层厚度为121mm。这个优化结果是不同于针对单个目标获得的优化结果,单独考虑全生命周期能耗、全生命周期碳排放、全生命周期总成本时的最佳保温层厚度分别为110mm、130mm、110mm。分层多目标优化获得的结果,是介于多个单目标优化结果之间,这也说明,多目标优化结果是在各个单目标中寻求平衡与折中,通过本文给出的优化方法,能在综合考虑能耗、碳排放和总成本三个因素的条件下,给出保温层厚度的唯一优化结果,方便使用者决策。
